图论
hegm
·
2022-10-29 15:21:28
·
个人记录
分层图
对于有些最短(长)路,有一些特殊操作,能使得图整体不发生变化。
经典问题:飞行路线
有 k 次免费的机会。
考虑建 k+1 层图,图与图之间并列,每次的免费可以视作从 i 层图的 u ,到 i+1 层的 v 消耗本来是 val ,现在变成 0 。由于只有 k 层图,所以直接跑 dij/spfa 都只会最多有 k 次免费的机会。
最后答案为 \min\limits _{i=t,i+=n}^{(k+1)\times n} dis_i 。
LCA
终于开始补郑瑞的题目了。
首先看到多个点的 \text{LCA} 想到区间 lca ,但是发现和题目要求没有关系,因为他是让你求 \sum 而不是整体。
首先,题目要求的是求出和某个值的 lca 的深度,这个可以转化成什么捏,可以转化为,将某个点向根节点的路径上全部付成 1 。然后求解路径上的和就好。
想到两种做法:
树上差分:修改区间内每一个点到跟的路径,使权值加一,然后暴力向上查询。
复杂度 O(n^2)
树链剖分,单次修改 log^2 ,查询 log^2 。
总复杂度 O(n^2log^2)
考虑优化复杂度 显然优化树剖
树剖的瓶颈在于,我们每次都需要 O(nlog^2n) 的暴力插入,但是我们发现可以离线
考虑将询问拆成两部分 l\to r 改为 [1\to r]\ \ \ -\ \ \ [1\to l-1] 。
我们可以离线下来,总复杂度 O(nlog^2n) 。
[GXOI/GZOI2019]旧词
和上面的没啥区别,只不过深度为 1 的每次加 1^k-0^k ,2 的每次加 2^k-1^k ,以此类推,这样的话就能求和得出深度的 k 次方了。
传送
大氵题。
首先考虑最基础的,维护每棵树的距离最近的两个叶子所在的位置。
考虑 dp ,dp_i 表示以 0 为跟的时候,在 i 所在的子树中,距离 i 最近的叶子结点。
正常 dp 一遍后,我们可以进行换根 dp 。
考虑 0 的子节点 1 。
$dp_1=\min(dp_1,dp_0+w(0,1))
注意在转移的时候,对于一个点 i 要选出最小和次小的 dp_j(j\in son_i) 。
直接求更新答案,即为 w_i 。(i 国家的最近叶子距离)
设 w_i 存储这个数。用一个 \text{ST} 表来进行区间查找。
现在初始工作都做完了,知道了:
用传送门经过某个国家所需要的最小时间(w_i )
某个点到距离他最近的叶子节点所需要的最小时间。
还需要维护一下 kl_i 表示从这个国家的根到这个城市的距离。
这样就可以使用树剖来维护树上两点距离。
开始分讨
1. 两个城市不在同一个国家
毫无疑问,需要从 s_0 到 e_0 国家(为了方便,保证 s_0<e_0 )
两个国家间传送的时间为 que(s_0+1,e_0-1)+(e_0-s_0)
毫无疑问,为了前往传送门,我们从 (s_0,s_1) 出发,去的叶子结点为它能到达的最近的,花费 dp_{(s_0,s_1)} 。同理,从传送门出来到 (e_0,e_1)
花费为 dp_{(e_0,e_1)} 。
ans=que(s_0+1,e_0-1)+(e_0-s_0)+dp_{(s_0,s_1)}+dp_{(e_0,e_1)}
2. 两个城市在同一个国家
两种情况,直接走国家内部,花费为树上距离。
也可以传送到相邻的国家,再传送回来。
但是会出现一个特殊情况,我们的 s_1 ,e_1 的最近传送门一样,但是门不能传送两次。
这种情况不用担心,因为要把两种方案取 \min ,而特殊情况出现时,是严格劣与第一种情况的。
所以可以放心大胆的计算。
对偶图
简单来说,对于原图的每一个面(不管是有界还是无界),我们认为是新图的一个点,两个面的公共边,我们认为是连接新图两点的边,边权直接继承下来。
注意一个易错点,对于一个图,外面这个整体是同一个点!
对于这道题,我们将起点和终点视为向左上方和右下方的两道射线,将外围的大面分为两个面,其中一个视为起点另一个视为终点,直接在对偶图上面跑 \texttt{dij} 即可。
[HNOI2009]最小圈
简化版题意,有向图找一个环 c_1,c_2\cdots,c_k ,使的他的 \mu(E)=\sum\limits_{1\le i\le k}(w_{c_i,c_{i+1}})/k 最大。
改变下形式 \dfrac{\sum\limits_{1\le i\le k}(w_{c_i,c_{i+1}})}{k} 看起来很像分数规划?
考虑二分 mid :
\dfrac{\sum\limits_{1\le i\le k}(w_{c_i,c_{i+1}})}{k}>mid
\sum\limits_{1\le i\le k}(w_{c_i,c_{i+1}})>k\times mid
\sum\limits_{1\le i\le k}(w_{c_i,c_{i+1}}-mid)>0
我们将 w_{c_i,c_{i+1}}-mid 设置为新的边权,在 mid 确定的情况下,我们发现,如果存在 \mu(E)<mid 就会在新的边权图上生成一个负环,我们可以通过 \text{SPFA} 进行判断:如果有 r=mid 否则 l=mid 。
------------
### [[SCOI2014]方伯伯运椰子](https://www.luogu.com.cn/problem/P3288)
依然是分数规划,先把原来的式子转化一下:
$\dfrac{X-Y}{k} \to \dfrac{\sum(abs(c_i-f_i)\times (-)d_i-cost(c_i-f_i))}{\sum abs(c_i-f_i)}$。($f_i$ 为 $i$ 现在的流量)
老规矩,分数规划二分 $mid$ 。
$\dfrac{\sum(abs(c_i-f_i)\times (-)d_i-cost(c_i-f_i))}{\sum abs(c_i-f_i)}<mid
将cost(c_i,f_i)=abs(c_i-f_i)\times a_i(b_i) 带入,移项。
\sum abs(c_i-f_i)\times ((-)d_i-a_i(b_i)-mid)<0
将 a,b,d,-d 拆分开。
当 c_i-f_i 为正时:
\sum abs(c_i-f_i)\times (-a_i+d_i-mid)<0
当 c_i-f_i 为负时:
\sum abs(c_i-f_i)\times (-b_i-d_i-mid)<0
我们考虑它的实际意义,观察二分性质。
我们二分出的 mid 对应的是 \dfrac{X-Y}{k} 的最大值,也就是说不存在\sum abs(c_i-f_i)\times ((-)d_i+a_i(b_i)-mid)>0
如果我们在原本的图的基础上建立一个新图:
那么如何判断是否有大于 0 的情况捏?
同时还要注意一个隐藏条件,每个点的出入度是不变的,也就是说我们要选一个环使得他的和大于 0。
我们发现不好判断,判正环那比的上判负环。
所以我们把边权全部都乘上 -1 。
问题得解,只需要在新图之上判断是否存在负环即可!
若有负环,说明 mid 太小。否则是 mid 太大。
注意,你的 v_i\to u_i 的前提是 c_i>0 。
[JSOI2016]最佳团体
又双叒叕是分数规划。
二分 mid 。 \dfrac{\sum P}{\sum S}<mid 。
转化为树形背包,求解最优值。
同时还得保证人数至少为 $K$ ,我们是用老方法, $dp_{i,j}$ 表示 $i$ 极其子树,占用空间恰好为 $j$ 的最大权值。
------------
### [[SDOI2017]新生舞会](https://www.luogu.com.cn/problem/P3705)
考虑到求的是最大值,我们二分 $mid$。
$\dfrac{\sum a}{\sum b}<mid\to \sum a<\sum b\times mid\to\sum (a_i-mid\times b_i)<0
问题转化,我们考虑这个式子的实际意义是对男生女生进行二分图匹配,匹配是有代价的,两个人匹配的代价为 a_{i,j}-b_{i,j}\times mid 。
那么考虑二分的具体内容,我们只要证明当前的 mid 存在 \sum (a_i-mid\times b_i)>0
即可,如果存在 r=mid 否则 l=mid 。
问题是如何证明/寻找最大的 \sum (a_i-mid\times b_i) ,不难发现,它类似于费用流的形式,同时又因为网络流兼容二分图,所以我们可以通过找最小费用最大流来寻找最小值,既然是找最小值,我们就要把边权变为 mid\times b_i-a_i 进行寻找。
[USACO07DEC]Sightseeing Cows G
分数规划,所以二分 mid 。
不难得出式子:
\dfrac{\sum val_i}{\sum t_i}<mid\to \sum mid\times t_i-val_i>0
这里的 val_i 对应的是 i 这条边的起点的美丽值。
我们需要证明 \sum mid\times t_i-val_i<0 不存在,即判断有无负环。
如果有 l=mid 否则 r=mid 。
跳楼机
同余最短路,终于学了 : )
本质就是让你求出一条长度为 m(mod\ p) 的最短路使得到达的对应点的编号最小。
简单 dp 即可。
【模板】点分治1
点分治的分治点,在树的重心(最大子树最小的点)。
用一个桶进行存储。复杂度 n\log n 。
机棚障碍 Hangar Hurdles
重构树题目。
蛮复杂的,拿来练练手。
考虑二维前缀和维护每个点能扩散的最大正方形,
先考虑左上角(其余同理)
当前到了 (i,j) 设:
l=ans_{i,j-1}$, $r=ans_{i-1,j}$,$m=ans_{i-1,j-1}$,$now=ans_{i,j}
暴力分讨
l=r\le m →now=l+1
l=r> m →now=l
l\ne r →now=\min(l,r)+1
同理维护出 左下,右下,右上。
合并答案: \ \ 取四者中最小的。 ans=\min \times \ 2-1 。
注意, ans 要去负为 0 。
这样我们就维护出了每个点,一共 n^2 个点,向上下左右连一条 \min(ans_u,ans_v) 的边,直接跑就行(吗?)
发现边太多了,会 \text {TLE} 。
我们发现,相邻的点的 ans 如果相等,可以看做是一个点,我们考虑合并,使用 \text{BFS} 。
跑 \text{Kruskal} 重构树即可。
### [[ARC098F] Donation](https://www.luogu.com.cn/problem/AT_arc098_d)
第二次遇见在 $\text{Kruskal}$ 重构树上跑 $\text{dp}$ 。
很烦,题目和 [Labyrinth](https://www.luogu.com.cn/problem/CF1578L)十分相似,但是不在是边权,而是点权。
回想起无耻老贼 `smeow` ,有一道类似的题目。
考虑两个点的先后顺序 ,两点为 $u,v$ 。 $sum$ 表示当前的钱数。$s$ 为限制, $c$ 为花费。(保证 $sum>c_u+c_v$ )
两个条件:
① $sum-c_u\ge s_v$ 可以先去 $u$ 再去 $v$。
② $sum-c_v\ge s_u$ 可以先去 $v$ 再去 $u$。
大力分讨:
1. ① $\&$ ② 两者不需要考虑顺序。
2. ① $\&$ $!$② 必须先去 $u$ 才能再去 $v$。
3. $!$① $\&$ ② 必须先去 $v$ 才能再去 $u$。
对于情况 2. 我们满足
- $sum-c_u\ge s_v \ \ \ \& \ \ \ \ sum-c_v<s_u
我们发现,哎!这样的话每个数之和自己有关系了,太好了。
那么设 t_i=s_i-c_i
我们第一时间想到的是按 t_i 排序,然后就做完了,好的,你就错完了。
对于每条边,我们将它的边权设置为 \max(t_u,t_v) 。
转移方式同Labyrinth。
Cheap Robot
很妙的一道题(看了题解后)。
自己推一遍。
发现题目是另类的最小瓶颈路,或者说是最小瓶颈路和最短路结合。
有 k 个关键点,考虑对于每一个普通点,维护出距离他最近的关键点和他的距离(dis )。
可以通过建立虚拟原点,向每个关键点连边,直接 \text{dij} 即可。
现在抽象的想我们正从 a 点到 b 点。
在这个过程中,我们到了 c 点,当前电池剩余电量为 now 。
那么这时,总电量至少应该是多少哪?
我们我们从一个充电桩到 $c$ 花费至少为 $dis_c$,所以总电量 $s\ge now+dis_c$。
整个不等式就是:$s - dis_c \ge now \ge dis_c$ 。
我们考虑我们下一个目标点是 $d$ 。
我们依然要保证 $now-w_{c,d} \ge dis_d$ 。
$s-dis_c-w_{c,d}\ge now-w_{c,d}\ge dis_d $ 。
把中间的忽略掉。
$s-dis_c-w_{c,d}\ge dis_d$ 。
移一下项 $s\ge dis_c+w_{c,d}+dis_d$ 。
重置一下边权。
直接重构树,求出两点间的最小最大边权。
$\text{time:}\ \ \ 7:15-7:45
------------
### [Company](https://www.luogu.com.cn/problem/CF1062E)
区间 $\text{LCA}$ 模板题。
区间 $\text{LCA}$ 即为 $dfn_{max},dfn_{min}$ 的$\text{LCA}$ 。
本题讨论删去最大,最小,两者取 $\max deep$ 即可。
$\text{time:} 8:55-9:48
------------
### [Groceries in Meteor Town](https://www.luogu.com.cn/problem/CF1628E)
这道题需要上面内道的思路。
考虑建树,由于两点间路径唯一,所以需要查询两点间的最大可能权值,即为两点间的最小瓶颈路,建立最小 $\text{Kruskal}$ 重构树。
因为点权从下到上为升序,所以我们的目的是让给定的 $x$ 点和所有白点的 $\text{LCA}$ 深度最小。
使用上一道题的思路,多个数 $\text{LCA}$ 为 $dfn_{max},dfn_{min}$ 的 $\text{LCA}$ 。
那么 $ans=\max(\text{lca}(x,dfn_{max}) , \text{lca}(x,dfn_{min}))$ 。(这里的 $dfn_{max,min}$ 都是白点的最大最小)。
那么 $3$ 操作解决了。
如何解决 $1,2$ ?
建出一颗线段树,存储所有点是黑点,还是白点, $\text{push\_up}$ 的时候统计出所有白点的 $dfn_{min,max}$ 。
做完了
$\text{time:}\ \ \ 10:25-11:36
挂了一发,下午来了开始改,改了 40min 。总算过了,错因是 lztag 传错了。
werewolf 狼人
听说这玩意好像叫上下界重构树?
考虑每个边的边权,我们先生成一棵树,用来表示人的行走路线。
那么 u→v 边权就是 \min(u,v) 。
生成一棵下界重构树,考虑起点是 s ,我们从 s 出发,找到我们能去的 id 最小的点(边)。
那么我们就知道了所有作为人,能去的点,是祖先的子树。
同理搞一棵上界重构树,起点是 e ,找到所有作为狼人能去的点。
现在我们就知道了两种状态所能到的所有点。
考虑取交集。发现并不好做。
联想到 Peaks,考虑我们的树,用叶子的 dfn 生成两个排序。
问题就转化为了,给你两个排序求第一个排列的 [l_1,r_1] 和第二个排列的 [l_2,r_2] 是否有数同时出现过。
很熟悉啊,看看这道题 Two permutations
我们需要一个小技巧,使用求 \text{LCS} 时的方法,将第一个序列变为 1,2,3\cdots n 。同时将第二个序列进行映射,使得他们的关系不变。
那么我们就可以使用可持久化线段树来维护了。
\text{time:} 15:35-9:04
都第二天了,吐了,翻了一遍题解,发现做法一毛子一样,起点特殊情况到底怎么处理啊啊啊啊啊啊。
调完了,小丑了,发现人和狼弄反了。
------------
### [摩托车交易](https://www.luogu.com.cn/problem/P3280)
重构树题目,非常简单啊。
[传送门](https://www.luogu.com.cn/problem/P3280)
很显然,让你顺次求两点的最小瓶颈路。
但是问题在于列车,可以使得最小瓶颈路被打乱。
考虑正常情况下的最小瓶颈路,走到两点的 $\text{LCA}$,然后返回 $\text{LCA}$ 的 $val$ 即可。
但是因为列车站的原因,我们的路径由 $u\to c\to v$ 变为了 $u\to a\to b\to v$。(其中 $c$ 为 $u,v$ 的 $\text{LCA}$,$a,b$ 均为列车车站)。
答案就变为了
$ans=\max(val_c,\min(val_a,val_b))$。
那么我们怎么找没对 $u,v$ 的 $a,b$ 哪?
考虑实际过程,当 $u\to c$ 的倍增过程中。遇到了一个点 $d$, $d$ 的子树中包含了一个列车站点,那么答案一定不再是 $val_c$ 了,因为我们的 $deep_d>deep_c$,又因为重构树的性质,$deep$ 越大,说明 $val$ 越大。
那就好做多了,我们只需要更改下 $\text{Kruskal}$ 重构树的建树过程,对于一个重构点,多维护一个 $vis$ 表示子树中是否有列车车站即可。
那么我们就求出来了 $u,v$ 两点间的最小瓶颈路。
那么我们只需要按照顺序进行交易即可,
具体的,我们设 $now$ 表示当前的黄金数量,每到一个补充黄金的地点,我们就把 $now+=b_i$,每到一个卖出黄金的地点,我们就把 $now=\max(0,now+b_i)$。同时输出答案。
做完了
$\text{time:} 10:30-11:00
挂了一发,注意从 1\sim n 的点要特判一下是否本身就是车站。
Graph and Queries
发现是删边操作,不好搞。于是我们到这来,先把询问离线下来,对于删除的每一个边,打上标记,用没打上标记的边建图,不难发现有多个连通块,把每个连通块看做是一棵树,建立重构树,将重构树的新点时间权值设置为 inf 。
这样我们就有了一个重构树森林,考虑每次的加边操作,相当于与将两棵树合并。(如果两点在同一棵树内则不予理会)
这样的话我们就在重构树森林上多出了一个点,将这个点的时间权值设为操作的时间权值。
那么某次询问,就变成了我们从 v 点跑祖先一直找到一个点使得他的 time 大于我们操作的 time 并且最小,在查找他的子树内部的最大值。
可以在建完树后用 dfs 拍成序列用线段树维护。
道路相遇
圆方树板子题,考虑对原图建出新的圆方树,那么两点之间的路径必须经过的点其实就是两点间的割点,割点是在书上的非叶子圆点,那么直接统计路径上的圆点个数即可。
个数不用麻烦的求解,直接用深度差即可求出,最后再加上二,因为 u,v 也是必须经过的点。
[APIO2010] 巡逻
先考虑 k=1 ,显然找出树上的最大直径,那么答案就是
那么考虑 $k=2$ 的时候,我们保持之前的思路,仍然先找出直径,这个时候我们发现,把直径从树上剖去,剩余的是森林。
如果我们连接同一棵树之内的两点,那么贡献就是两点的距离,如果我们连接的不是同一棵树的点,容易发现,我们连接的两点间的路径(不包括第一次剖走的部分)只会经过一次,~~手模~~可以发现,这之间经过的(第一次剖走)边又会在经过一次。
这样的话(第二次)对答案的贡献就是:两点间的边数-经过的第一次剖的边数。
怎么让这个最大?直接将第一次剖掉的边改为 $-1$ 即可,然后再次求直径。
------------
### [The Ministers' Major Mess](https://www.luogu.com.cn/problem/UVA1086)
有点诈骗的题目,我们对提案数量进行分讨。
1. $1\sim 2$ 每个都必须通过。
2. $3\sim 4$ 只能不通过一个。
容易发现直接上 $2-\text{sat}$ 搞就好了,但是特别的是他有判断 $?$ 的情况,加入我现在已经有了一组方案,那么我们对于某一个点强制让他选和之前不同的即可,如果这样还有方案,那么说明他选什么都无所谓。
可能 $?$ 之间互相影响,但是题目中的定义是只要有两种方案让 $i$ 有 $n,y$ 两种情况即可,所以每一个点之间是独立的。
暴力每个点跑就好,复杂度 $O(n^3)$。
------------
### [[ABC210F] Coprime Solitaire](https://www.luogu.com.cn/problem/AT_abc210_f)
考虑对于值域范围内的每一个质数 $p$。
将所有 $a_i/b_i$ 能被当前质数整除的都找出来:
- 如果 $a_i$ 能被 $p$ 整除,那么我们将 $i$ 放入。
- 如果 $b_i$ 能被 $p$ 整除,那么我们将 $i+n$ 放入。
那么我们对于当前的整个数组 $c$ ,如果 $c_i$ 选了,那么 $\forall_{1\le j\le n\&j\ne i}\ \ c_j$ 这些就必须不能选。
所以对于某一个点 $i$ 我们要向所有的 $\neg c_j$ 连边。
容易发现这样的复杂度是 $n^2$ 的,所以我们考虑换一种连边方式,我们多添加 $n$ 个点 $f_{1\sim n}$。
其中 $f_i$ 向 $f_{i-1}$ 和 $\neg c_i$ 连边,特殊的 $f_1$ 只向 $\neg c_1$ 连边。
然后对于 $c_i$ 我们连边向 $f_{i-1}$。
容易发现我们的 $c_i$ 就可以间接只向 $\forall_{1\le j< i}\ \neg c_j$。
这就是前缀优化建边,同理我们可以搞出后缀优化建边,所以我们就可以在 $O(n)$ 的复杂度里面连出效果相同的边。
容易发现,我们直接筛出所有质数是行不通的,所以我们要对于每一个数进行质因数分解,对于每一个质因数,我们需要将他放入对应质因数的 `vector` 里面。
------------
### [[SDOI2016]数字配对](https://www.luogu.com.cn/problem/P4068)
很炫酷的网络流。
考虑一些奇怪的东西,对于一个网络流,难点在于确定我们的图结构。
我们思考 $n$ 个数字之间配对的关系:
> 若两个数字 $a_i,a_j$ 满足 $a_i$ 是 $a_j$ 的倍数,同时 $a_i/a_j$ 是一个质数。
这个条件很长,我们不妨把它换一下:
> 如果两个数字之间的关系满足: $a_i=a_j\times p$($p$ 为质数)。
这个条件就比较清晰了。
我们知道我们要建立出网络流二分图,所以我们需要知道左侧和右侧的点都有哪些。
那么如何将这些数字分类能保证同侧之间不会连边?
我们观察式子 $a_i=a_j\times p$,实际上是 $a_i$ 比 $a_j$ 多了一个质因子。
那么假如我将每一个数字 $a_k$ 进行质因数分解,设 $s_k$ 表示他的质因数个数,那么 $a_i$ 和 $a_j$ 连边必须要满足的条件就是:
> $s_i-s_j=1
容易证明这是必要条件,如果 s_i-s_j\ne 1 ,就说明 a_i 和 a_j 之间不止差了一个质因子,那么 a_i/a_j 就绝对不是质数。
那么我们按找 s_i 的奇偶性来建图,奇数的放在左边,偶数的放在右边。
这样我们就能保证同侧之间是不会连接的。
从而我们得到了一张完美的二分图。
那么如何保证总价值大于 0 ?
我们的总价值是一个单峰函数(证明就算了)
因为它只有一个 0 点。
所以我们可以二分匹配数量(最终流量),我们对于原本的汇点,再设置一个超级汇点,汇点向他连一条容量为 mid (二分结果)的边,这样我们就能强定他的配数量为 mid 然后看权值是否大于 0 然后继续二分即可。
树上游戏
考虑 n^2 和以上的复杂度,我们假设 s_{i,j} 表示和 i 的路径颜色中含有 j 的点的个数。
那么 sum_{i}=\sum\limits_{j=1}^m s_{i,j} (m 表示颜色数量)
我们对于每一种颜色 p 如果将 \forall_{1\le i\le n}c_i=p 的点都删掉,就会形成一片森林,对于森林中的每一棵树,容易发现树中任意两点间的颜色不包含 p ,而不在同一棵树中的则一定包含 p ,而删掉的点和任何一个点之间又有颜色 p (本身即为此颜色),所以 s_{i,p}=siz_{i,p} (siz_{i,p} 表示删除了颜色 p 后, i 所在连通块的大小)。s_{i,p} 就是和 i 的路径上不经过 p 颜色的点的数量。
但是这样效率低下,因为我们不但要删点,还要枚举删除那种颜色。
我们先解决删点问题:
我们现在在最上方的红色点,那么我们应该将三个红色点删掉形成大小分别为 1,2,3 的连通块,假如我们已经知道了连通块的大小,考虑一种不枚举所有点的方法,来更新每个点的 s_{i,p} ,假如说对于一个连通块 A (以大小为 3 的连通块为例子),我找出他深度最小的点 u (蓝色点),给他打上一个大小为 siz_{u,p} 的标记,然后对于和这个连通块相邻且深度比 u 大的红色节点,打上一个 -siz_{u,p} 的标记,对于这个标记我们可以做树上差分,一个点的权值为它到根节点的路径的权值和。
容易发现,这样也不用枚举颜色了,因为我没有实际删掉点,所以对于 i 号节点,我对于他的所有孩子做这种操作即可。
具体的,对于 i 号节点,遍历所有的 j\in son_i ,对于每一个 j ,我只求出他自己所在连通块的大小即可,然后做树上差分。对于上图中的大小为 2 的连通块,他会在最左侧的红色节点被 dfs 的时候做此操作,而不是最上方红色节点被 dfs 时。
现在有两个问题:如何动态的求出 siz_{i,p} 以及找到和 i 所在连通块相邻且深度更深的颜色为 p 的节点。
不难发现 siz_{i,p} 就是 i 的子树大小减去所有颜色是 p 的极大子树大小和。用人话说就是找出所有在 i 的子树中颜色是 p 的点并且他和 i 之间没有颜色为 p 的点,然后用 size_i 减去他们的子树大小和。
我们考虑用一个桶来维护 t_i 表示颜色为 i 的点的极大子树大小和。
我们考虑 dfs 到了节点 i 此时 t_{a_i} 里的值是在 i 外面的子树大小和,与 i 无关,我们处理完所有 j\in son_i 后此时有 t_{a_i}' ,容易知道 t_{a_i}'-t_{a_i} 就是 siz_{i,a_i} (这里用 siz_{i,a_i} 是因为我们只会处理当前节点的颜色,别的颜色会在别的点处理,然后差分增加给当前点)
那么现在我们做完了 i 号点了,应该更新 t_{a_i} 了,那么 i 会顶替所有在他子树中的极大子树点,所以 t_{a_i}+=size_i-siz_{i,a_i} 。
最后我们来思考如何找出所有的极大子树点。
容易发现,这和上面的区别不大,我们使用一个 stack 来存储。
然后进行一开始想好的树上差分操作即可。
补充一点,如果我们这么算的话会发现 $i$ 号节点的贡献少自己颜色的贡献,因为计算 $i$ 的时候容易发现 $i$ 自己并不会被打上标记,所以对于每一个 $sum_i$ 我还应该增加 $n$。
------------
### [Tree and LCS](https://www.luogu.com.cn/problem/AT_arc156_c)
题目大意:
我们定义一个排列 $A$ 和$B$ 的相似性为 $S_i=B_{A_i}$, $S$ 和 $A$ 的最长公共子序列。
我们需要找到一个排列 $P$ 使得和给定树 $T$ 的所有简单路径的相似性的最大值最小。
先证明下这个相似性的最小值。
假如对于排列 $P$,我们肯定可以通过选择路径 $A:x\to P_x$,这样的话 $P$ 和 $A$ 的 LIS 即为 $1$ 了,此为答案的下界。
现在我们不妨想一想如何构造或者证明存在一种方式使得我们可以保证答案就是下界。
~~既然你们都说了不用想到,那就不说了~~
考虑如下的一种神奇的构造方式:
我们将原树的所有叶子拎出来,放入一个队列。
1. 从队列中取出两个点,$u,v$,将 $P_u=v,P_v=u$。
2. 将两个点从树中删掉,然后将新生成的叶子放入队列中。
3. 重复操作直到只剩下一个叶子或者什么都不剩(剩下的一个叶子 $i$,$P_i=i$)
下面来证明为什么这样可以保证答案为 $1$。
首先,对于原图中的所有边,我们只选取极大路径,容易证明这时最大值肯定在这里面。
那么对于一个极大路径 $u\to v$,我们从中找出 $x,y$。

我们假设 $A,P$ 的 LIS 中包含 $x\to p_y$,换句话说,在上述步骤中, $x,y$ 被匹配并且同时删掉了。
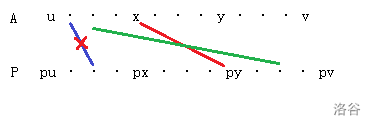
图中边表示匹配。
那么对于 $A$ 中,位置在 $x$ 前的某一个点 $k$,他的匹配对象有两种可能:
1. 在 $u\to v$ 的路径中。
2. 不在 $u\to v$ 的路径中。
第二种情况不影响我们的 LIS 我们直接忽略。
考虑第一种情况中,和 $k$ 匹配的 $s$ 的位置。
我们判断 $k\to s$ 是否有可能对 LIS 产生贡献,只需要看 $s$ 在 $A$ 中和 $y$ 的相对位置即可。
我们可以证明 $s$ 如果存在在 $A$ 中,那么一定在 $y$ 的后方。
首先,原树是一棵无根树,我们不妨找一个根来帮助我们判断,我们让根是最后删除点/点对。(容易证明,如果最后存在两个点,那么他们一定是相连的)
在这棵树上有一个性质,对于某个节点 $p$,先要删除他就一定要把他的孩子都删除完。
借助这个性质,我们可以知道 $x,y$ 一定不是祖先关系,因为你要想删掉其中深度较小的点,肯定要先删掉深度更大的点。
我们设 $x,y$ 的 $\text{lca}$ 为 $c$。
那么树肯定是长这样的。
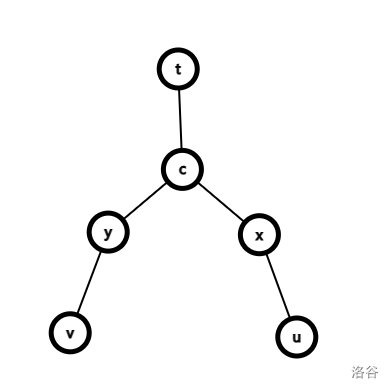
而 $k$ 一定在 $x$ 的子树中,肯定先于 $x$ 被删除,既然如此,那么和他抵消的 $s$ 一定会在 $y$ 的子树中。如果不是,有两种可能:
1. $s$ 在 $c\to u$ 的路径中,那么 $s,k$ 存在祖先关系,假设不成立。
2. $s$ 在 $y\to x$ 中,那么想要删除 $s$,至少得先删除 $x,y$ 中的某一个,但是根据上方所说, $k$ 比 $x$ 先删除,互相矛盾,假设不成立。
那么,我们就完美的证明了它的正确性。
------------
### [Opening Portals](https://www.luogu.com.cn/problem/CF196E)
很神奇的一道题目。
考虑将题目转变为一步一步。
出生点在 $1$,那么我们先贪心的去一个最近的传送门。(自己也是的话就不动)。
那么接下来是选定一个已经被标记的传送门,然后向另一个没有被标记的传送门前进。
重复上述步骤直到所有所有传送门都被标记。
如何保证价值最小?
不妨参考 $\text{Kruskal}$ 的过程,每次贪心的将最近的两个传送门连接,构成连通块。
问题转变为如何求出这个最近距离。
现在着眼于原图的边,某一个边如果被经过,那么会用于什么时候,或者说从 $u\to v$ 的时候,会经过这个边,那么这个边对应的 $u,v$ 是什么。
一条边 $a\to b$ 权值为 $w$。
那么他会连接的两个传送门应该是 $kl_a\to kl_b$ 边权为 $w+dis_a+dis_b$。
$dis_a$ 表示的是距离 $a$ 最近的传送门,$kl_a$ 表示的是这个传送门是啥。
------------
### [[ZJOI2017]仙人掌](https://www.luogu.com.cn/problem/P3687)
先排除掉原图已经仙人掌的情况。
对于在原图上的已经有简单环的部分,由于新连接的边不可能跨过他,所以可以直接断掉,此时原图形成了森林,只需要对于每棵树求解,最后乘起来就好了。
现在考虑一棵树,容易发现,我们的操作相当于每次给树上的一条链子打上标记,并且每条边不能被重复打上标记,求给所有边打上标记的方案数。(给 $u\to v$ 打标记,相当于链接一条 $u\to v$ 的边)
关于为什么都要打上标记,考虑如果一条边单独被一次操作打上标记,因为这这条边 $u\to v$ 连接了一个重边,形成了一个环,那么只需要将重边断掉就好了,这样的方案依然是一个仙人掌。
$f_s$ 表示一个点有 $s$ 个孩子的时候,将 $s$ 个孩子的链子全部打上标记的方案数。
这玩意可以递推,每次可以选择链接一条 $i$ 号点到 $u$ 的链底,也可以选择之前的某一个孩子 $v$ 对 $v\to i\to u$ 这条链子操作。
$f_s=f_{s-1}+(s-1)\times f_{s-2}$。
容易发现 $f$ 数组,不会受到树形的影响,只和孩子数量有关,因此 $f$ 直接预处理就好。
注意,此时不要考虑不连接向 $u$ 链子底的情况,因为 $u$ 到 $i$ 的链子有多重情况,如果不连接向 $u$ 的链子底,剩余的多余长度不管怎么连接都会规约到 $u$ 的方案数中。
那么考虑现在在树上转移。
$g_i$ 表示 $i$ 子树内只剩一条链子没有被覆盖,其余边都被覆盖的方案数。
两种情况:
1. 将所有的孩子全部填死,只剩下 $i\to fa_i$ 一条边作为链子。此时方案数: $f_{siz_i}\times\prod\limits_{u\in son_i}g_u$。
2. 留下一条链子,那么其余的要填死。此时方案数: $f_{siz_i-1}\times i\times\prod\limits_{u\in son_i}g_u
所以 g_i=(f_{siz_i}+f_{siz_i-1}\times i)\times\prod\limits_{u\in son_i}g_u
特殊的,根由于不需要向外延伸,所以答案就是 f_{siz_i}\times \prod\limits_{u\in son_i}g_u
[HNOI2014]世界树
比较简单的一道题目,考虑对每次询问的点缩虚树,那么对于虚树上的点,找到距离他最近的关键点(包括祖先中的,换根 dp 即可),那么对于虚树上的每一条边(对应原树的一条链子),我知道了距离它两段最近的点分别是什么,那么贡献很好算(注意还要处理挂在上面的子树,找到分割点用子树大小作差就好了)。
同时考虑不在虚树上的点,那么它的贡献就是祖先中第一个在虚树上的点对应的关键点,我们可以在祖先统计。
细节有一点多 : )
[HNOI/AHOI2018]毒瘤
考虑普通的树上独立集 dp。
$f_{i,0}=\prod\limits_{u\in son_i} f_{u,0}+f_{u,1}
f_{i,1}=\prod\limits_{u\in son_i}f_{u,0}
现在考虑每一条非树边的限制,假如是 u\to v 那么两次考虑,u 选,那么 f_{v,1} 清零,重新做一遍。否则 u 不选,v 随意,f_{u,1} 清零重新做一遍,那么又因为有 11 个限制,所以是 2^{11}\times n 的复杂度。
但是容易发现,更改后只有非树边的路径上的点的 f 会发生变化,但这还不够,因为数量级别还是 O(n) 的。
那么我们对这 22 个特殊点建出虚树,那么考虑虚树上的一条边的实际上可以怎么转移,结论就是一条边(连接 u,v 且 dep_u<dep_v )可以写成 f_{u,0/1}=a\times f_{v,0}+b\times f_{v,1} 也就是一个常数倍。
一些小细节:对于虚树上的一条边,暴力跳到边顶的时候注意不能直接乘上权值。
在虚树上的点的不在虚树上的儿子要特殊统计。
[SDOI2011] 消防
考虑只有一个点的时候怎么做,显然就是在原本的直径上找到一个点,那么扩展边也只可能以此为基础扩展。
考虑对于每一个节点按照直径重心为跟,处理出子树内的最远点的距离以及对应的是哪一个点就好了。
然后就可以贪心的跑dp,因为除了重心,其余的点都只能被迫的向最远点连边
[NOI2020] 超现实树
神仙题。
考虑有那些树不能被同深度的其他树生成。
对一棵树重链剖分,如果他的链长只有 x 和 1 那么这棵树不能有其他同深度的树生成得来。
形式化的,其实就是一条长度为 dep 的链子上挂了一些叶子,这样的树不能被同深度的树生成。
那么考虑有什么用,如果某个森林,它不能生成的树的深度都相同,那么显然,这个森林是几乎完备的,因为深度固定的树深度是有限的。
而对于之前讨论的树,它既然不能由同深度的树生成,只能有深度更小的生成。
那么不妨建出一张图,图上的一条有向边 A\to B 表示 A 能生成出 B 。
容易证明,这张图一定是个 DAG,因为生长一定是增加节点,所以不存在环。
那么对于同深度的树构成的层,入度为 0 的点,一定是无法被同深度生成的特殊树。
现在换个想法考虑,假如入把这个无限大的图看做二分图:
将深度为 x 的所有特殊树看做一个点,放在左侧的第 x 个点(从上到下)。
同理,深度为 x 的非特殊树看做一个点,放在右边的第 x 个点。
考虑这个图的连边,不难发现,现在图上的一个节点是属于一个集合。
考虑从左向右的同层点有一条边,因为右侧的点集内的所有的树都可以有左侧点集的树生成。
而不同深度的点,深度为 x 的会有一条向深度为 [x+1,\infty] 的左侧和右侧点连边。
现在考虑什么情况下,一个图是几乎完备的:
当且尽当,有一个左侧点里的集合里的树都可以被生成。
考虑什么时候一个图不是几乎完备的,也就是说没有一个左侧的点的集合里的树都可以被生成。
我们发现整个过程和右侧的树没有关系,因此可以将右侧的所有树删掉。
那么现在只有特殊树了,考虑特殊树是如何生成 [x+1,\infty] 的特殊树的。
那么如果 A 能生成 B ,必须保证 B 的深度为 x 的部分和 A 整体一样。
考虑每一棵树在沿着重链向下走的过程中,每一层会有几种选择。
当前层只有一个左孩子。
当前层只有一个有孩子。
当前层只有既有左孩子也有右孩子,并且重儿子是左孩子。
当前层只有既有左孩子也有右孩子,并且重儿子是右孩子。
那么这个无限大的只包含特殊树的图就可以看做是一颗无限大的四叉树,每个点都对应了一棵树。
考虑将一棵特殊树放入到这个图上,只需要沿着节点含义一个一个走就好,特殊的,如果一棵树的最深节点有两个,那么他的终止节点也有两个,对应着 3,4 。
将特殊树插入后,将所有经过的节点打上 vis 标记,并且给终止节点打上 ed 标记。
考虑将所有特殊树插入之后,什么情况下是无解的。
当且仅当,从根节点出发,在不经过 ed 的点的情况下,可以走到一个没有 vis 的节点。
P8499 [NOI2022] 挑战 NPC Ⅱ
考虑暴力,对于 i 号位置,先将所有合法的子树全部都匹配上,剩余的不会超过 k 个,然后 k^2 的暴力枚举匹配,加一些剪枝:
假如当前已经有 m 个不匹配了,同时现在 a\to b 的匹配点数差了 k-m+1 以上,那么显然不合法。
哈希不同大小相同认为不合法。
H 的反而大于 G 的大小,不合法。
【模板】最小斯坦纳树
本质就是在无向图上求出 k 个关键点的虚树。
由于是在无向图上了,所以复杂度不是多项式级别。
显然需要状态压缩,f_{i,s} 表示以 i 为根节点,并且此时的树包含关键点的情况为 j 时的方案数。
注意,这个根节点只不过是为了转移钦定罢了,所以说对于一棵树,任何一个点都可以当做根。
那么考虑转移,第一种转移是增加一个点 j ,花费是 dis_{i,j} ,也就是说将 j 作为新的树根,然后将 i 接到 j 低下。
这种情况可以类似 dij 跑出来。
第二种情况,将多个 s 接到 i 的下面,所以需要枚举子集。
for(int i=1;i<=lim;i++)
{
for(int j=1;j<=n;j++)
{
for(int p=i;p;p=i&(p-1))
dp[j][i]=min(dp[j][i],dp[j][p]+dp[j][i^p]);
}
dij(i);
}注意,一定要先进行二情况才能做一情况,因为dij的初值是通过二情况求出来的。
TICKET - Ticket to Ride
斯坦纳树的例题,但是要求的是让 4 对点分别联通即可。
考虑先对原图求出最小斯坦纳树,那么数组 f_{i,s} 描述的就是联通性为 s 情况下的最小代价,注意,i 必须要是 s 中的一个点。
那么考虑枚举这四对点之间的联通情况,也采取状压,枚举一个 S 表示 连接情况为 S (S<2^4 ),表示终态为 S ,枚举 S'\in S ,用 dp_{S'}+dp_{S\oplus S'} 来更新 dp_{S} 。
实际意义就是让 S' 和 S\oplus S' 中的点互补联通,但是又满足两两联通的要求。
P3761 [TJOI2017] 城市
考虑本质上是让你删除一条边,然后链接一条边权一样的边使得直径最小,考虑随便删除一条边,那么如何连接能最小化直径,假设短边形成的两个树分别为 A,B 断开的边权为 w ,新链接的点对为 u,v 。
新树的直径为 A,B 的直径。
新树的直径为 len+dis_u+dis_v ,dis_u 表示距离 u 最远的点距离。
容易发现在枚举断边的情况下 1 贡献是确定的,而 2 贡献本质是找到 dis_u 最小的点。
但是这太简单了,所以考虑如何线性,容易发现 $dis_u$ 最小值是直径中点取到的。
先排除一些显然的情况,即,如果短边没有断在原树的直径上,那么对答案没有贡献。
所以短边一定断在直线上,因此直径的两段一定分别在 $A,B$ 树内。
考虑一个有趣的性质:原树直径的端点也一定是 $A,B$ 两树的直径端点。
证明可以考虑反证法。
因此,我们确定了两颗树内的直径端点,所以考虑把直径拉伸开。
从左到右的经过直径上的点,每次经过就新扫一遍维护出 $i$ 到左侧直径端点的距离。
同理,右侧也扫一遍即可。复杂度 $O(n)$。
但是尴尬的发现,由于带边权,所以不仅需要求出直径长度,还要求出直径中点的位置,容易发现,对于在直径上向左侧走的时候,右侧直径中点会发生变化,同时这个中点一定是在原树的直径上的并且一定是单调向右侧移动。
------------
### [Royal Questions](https://www.luogu.com.cn/problem/CF875F)
逆天题,遇见一道比赛题目过来的,本质上是最大权值基环森林。
但是看到这道题目的时候懵逼了,这道题目和最大权值生成基环森林有什么关系。
还是在看到输入的格式后才反应过来。
首先转化题意,即“最大权值生成基环森林”。
容易发现对于每一个公主,连接两个王子 $u,v$,边权为 $w$。
那么会形成一张无向图,由于目的是选择一个王子和一个公主匹配,权值为 $w$,所以容易发现可以转化为:对每个点选择至多一条出边,问边权和最大是多少。
由于每个节点最多一条出边,所以形成的图一定是基环树。又因为没有要求连通性,所以是基环森林。
因此转化为最大权值基环森林,考虑如何求最大权值基环森林。
考虑 $\text{Kruskal}$ 的过程,我们知道 $\text{Kruskal}$ 的本质是按照权值顺序枚举每一条边,看能否加入到生成树内。
所以考虑修改一下,对于每一个并查集,同时维护此并查集的点集组成的是树还是基环树。
对于一条边,如果他连接的两个联通快内至少有一个是树,那么可以连接。如果他连接的两点属于同一个联通快,那么只有当前联通快是树才可以,此时会从树变为基环树。
```cpp
#include<bits/stdc++.h>
#define N 200005
#define int long long
using namespace std;
int read()
{
int x=0,f=1;char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
return x*f;
}
int n,m,vis[N],s[N],a[N],fa[N],ans;
map<int,bool> mp[N];
struct edge
{
int u,v,w;
}k[N*2];int tot;
bool cmp2(edge x,edge y)
{
return x.w>y.w;
}
int find(int x)
{
if(fa[x]==x)return x;
return fa[x]=find(fa[x]);
}
signed main()
{
// freopen("contact.in","r",stdin);
// freopen("contact.out","w",stdout);
n=read();m=read();
for(int i=1;i<=m;i++)
{
k[i].u=read();
k[i].v=read();
k[i].w=read();
}
sort(k+1,k+1+m,cmp2);
for(int i=1;i<=n;i++)fa[i]=i,vis[i]=1;
for(int i=1,u,v;i<=m;i++)
{
u=k[i].u,v=k[i].v;
if(find(u)!=find(v)&&(vis[fa[u]]|vis[fa[v]]))
{
ans+=k[i].w;
vis[fa[u]]&=vis[fa[v]];
fa[fa[v]]=fa[u];
}
else if(fa[u]==fa[v]&&vis[fa[u]])
{
vis[fa[u]]=0;
ans+=k[i].w;
}
}
cout<<ans<<"\n";
return 0;
}
```
------------
### [Roads and Ramen](https://www.luogu.com.cn/problem/CF1413F)
和捉迷藏非常像。
考虑将点按照到根的路径上标记数量的奇偶性分类。
容易发现,在同一类的点之间是合法的。
现在需要证明一些奇怪的性质:
假如当前我们知道了一个集合的最远点对 $x,y$,那么我们考虑新加入一个点 $k$。
首先我们要在当前集合中选出一个点 $p$,使得 $p$ 距离 $k$ 最远,然后更新最远点对。
>性质:$p$ 是 $x$ 或者 $y$,不可能有其他选择。
尝试证明,我们考虑分类讨论。
1. $k$ 在 $x\to y$ 的路径上
这个很好想,必然 $p=x/y$。
如果存在一个点 $p(p\ne x/y)$,使得 $k\to p$ 的距离最大,那么我们就可以使用黄色的路径替换掉 $x\to k\to y$ 的$k\to y$ 这一段,获得更远的点对,可以推翻 $x,y$ 为最远点对,所以不存在这样的点 $p$。
2. $k$ 不在 $x\to y$ 的路径上
我们还是假设 $p$ 不是 $x/y$ 那么 $k\to p$ 的路径可以分为两种情况:
- $k\to p$ 的路径经过了 $x\to y$ 的路径
容易发现,和之前差别不大,既然 $y$ 不是 $k$ 最远点就说明 $w_{s,y}<w_{s,p}$,但是这样又会推翻我们的 $x,y$ 为最远点对的假设,所以这样的 $p$ 不存在。
- $k\to p$ 的路径不经过 $x\to y$ 的路径
那么如果 $k$ 距离 $x\to y$ 的路径比较近,就会成为图上的情况,我们知道红色边权大于 $s\to y+s\to k$ 的边权,既然如此,我们红色边权加上黄色边权肯定比 $y\to s$ 更大,那么我们的 $x,y$ 最远点对又被推翻了。
而如果 $p$ 距离 $s$ 更近,那么我们会发现,我们 $k\to p\to y$ 的路径多了一条边,而边权又是正的,那么加上肯定不亏,所以又能推翻上述假设。
综上我们推出了:
>$p$ 是 $x$ 或者 $y$,不可能有其他选择。
那么加入一个点就简单了,我们只需要求出它到当前最远点对的距离即可,复杂度是 $\log n$ 的。
现在我们考虑每次不是加入一个点,而是加入一个集合,换句话说,合并两个集合。
将 $B$ 集合加入到 $A$ 集合,我们先考虑暴力的一个一个往里面加,那么我们会枚举 $B$ 中的每一个点,我们设 $ans_i$ 表示 $B_i$ 和 $A$ 中的最远距离点的距离。那么我们每个 $B_i$ 都要和 $A_x,A_y$ 计算距离得到 $ans_i$。
然后在这些 $ans_i$ 中,再次取最大值。
这样很麻烦,我们不妨换一个角度,我们计算出所有 $B_i$ 到 $A_x$ 的距离取最大值记作 $ansx$,同理也可以得到 $ansy$,我们考虑 $ansx$ 和 $ansy$ 的值,是不是就相当于我将 $A_x$ 加入 $B$ 中的最远点对和将 $A_y$ 加入 $B$ 中的最远点对,又因为性质 $1$,最远点 $p=B_x/B_y$,那么性质就显而易见了,将两个区间合并,新的最远点对只会在两个区间的最远点对中产生!
这其实就是一个经典结论,可以优秀的用来维护直径(边权全为正数)。
那么转化到这道题目,我可以使用线段树维护区间信息,表示 $l\sim r$ 这个区间的直径,合并区间就如同上面合并集合一样。
然后这道题有一个特点就是分为两个大集合,那么分开维护就可以,更改一条边的标记就等同于子树修改,修改的内容是交换奇集合的内容和偶集合的内容,并且打上懒标记日后下传即可。
这道题很卡时间,可以用 $O(1)$ lca来优化,复杂度为 $n\log n$。
## CODE
```cpp
#include<bits/stdc++.h>
#define N 500005
#define ls (now<<1)
#define rs (now<<1|1)
using namespace std;
int read()
{
int x=0,f=1;char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
return x*f;
}
int n;
struct fig
{
int to,next,w,id;
}k[N*2];
int head[N],tot,dep[N],awa,cnt,id[N],st[21][N*2],dfn[N],siz[N],g[N],e[N],pl[N];
void add(int from,int to,int w,int id)
{
k[++tot].to=to;
k[tot].w=w;
k[tot].id=id;
k[tot].next=head[from];
head[from]=tot;
}
void dfs(int now,int f)
{
dep[now]=dep[f]+1;st[0][++cnt]=now;
dfn[now]=++awa;id[now]=cnt;siz[now]=1;
pl[awa]=now;
for(int i=head[now];i;i=k[i].next)
{
if(k[i].to==f)continue;
st[0][++cnt]=now;
e[k[i].id]=k[i].to;
g[k[i].to]=(g[now]^k[i].w);
dfs(k[i].to,now);
siz[now]+=siz[k[i].to];
}
}
int lca(int a,int b)
{
if(id[a]>id[b])swap(a,b);
int len=__lg(id[b]-id[a]+1),x,y;
x=st[len][id[a]];
y=st[len][id[b]-(1<<len)+1];
if(dep[x]<dep[y])return x;
return y;
}
int get(int a,int b)
{
if(!a||!b)return 0;
return dep[a]+dep[b]-2*dep[lca(a,b)];
}
struct line
{
int u,v,w;
}tr[2][N*4];int lz[N*4];
line merge(line x,line y)
{
line s;
if(x.u==0)return y;
if(y.u==0)return x;
if(x.w<y.w)s=y;
else s=x;
int p1=get(x.u,y.u),p2=get(x.u,y.v),p3=get(x.v,y.u),p4=get(x.v,y.v);
if(p1>s.w)s={x.u,y.u,p1};
if(p2>s.w)s={x.u,y.v,p2};
if(p3>s.w)s={x.v,y.u,p3};
if(p4>s.w)s={x.v,y.v,p4};
return s;
}
void up(int now)
{
tr[0][now]=merge(tr[0][ls],tr[0][rs]);
tr[1][now]=merge(tr[1][ls],tr[1][rs]);
}
void down(int now)
{
if(lz[now])
{
swap(tr[0][ls],tr[1][ls]);
swap(tr[0][rs],tr[1][rs]);
lz[ls]^=lz[now];
lz[rs]^=lz[now];
lz[now]=0;
}
}
void midy(int now,int l,int r,int ql,int qr)
{
if(l>=ql&&r<=qr)
{
lz[now]^=1;
swap(tr[0][now],tr[1][now]);
return ;
}
int mid=(l+r)>>1;down(now);
if(mid>=ql)midy(ls,l,mid,ql,qr);
if(mid<qr)midy(rs,mid+1,r,ql,qr);
up(now);
}
void build(int now,int l,int r)
{
if(l==r)
{
tr[g[pl[l]]][now].u=pl[l];
tr[g[pl[l]]][now].v=pl[l];
tr[g[pl[l]]][now].w=0;
return ;
}
int mid=(l+r)>>1;
build(ls,l,mid);
build(rs,mid+1,r);
up(now);
}
signed main()
{
n=read();
for(int i=1,u,v,w;i<n;i++)
{
u=read();v=read();w=read();
add(u,v,w,i);add(v,u,w,i);
}
dfs(1,0);dep[0]=1000000000;
for(int i=1;i<=20;i++)
{
for(int j=1;j<=cnt;j++)
{
if(dep[st[i-1][j]]<dep[st[i-1][j+(1<<(i-1))]])st[i][j]=st[i-1][j];
else st[i][j]=st[i-1][j+(1<<(i-1))];
}
}
build(1,1,n);
int q=read(),x;
while(q--)
{
x=e[read()];
midy(1,1,n,dfn[x],dfn[x]+siz[x]-1);
cout<<max(tr[1][1].w,tr[0][1].w)<<"\n";
}
return 0;
}
```
------------
### [Data Center Drama](https://www.luogu.com.cn/problem/CF527E)
思维题。
考虑拎出来一棵 dfs 树。
首先确定好入度,每个点可以通过给父向边定向来改变入度,所以现在只有根节点入度不一定为偶数,其余节点入度都为偶数。
考虑一个非树边的影响,他会改变其中一个节点的入度,另一个节点的出度。但是我们要尽量的维护所有节点(除了根)的入度都为偶数,所以我们可以把入度改变的点到根的路径上的所有边反向,那么效果是,非树边连接的两个节点的出度改变,根节点的出入度都发生改变。(一些特殊的自环,或者端点包含根的非树边也都满足这个性质)
那么最后,整个图除了根节点之外,所有点入度都是偶数,并且出度不确定。
那么我们考虑增加一条非树边,按照之前的思路,他会改变两端点的出度奇偶性,然后将根节点的出度和入度奇偶性都改变。
那么我们每次选两个非根节点的出度是奇数的,连接一条非树边。
那么最后三种情况:
1. 根节点的出度入度都是奇数,那么连接一个自环即可。
2. 根节点出度是奇数,入度是偶数,存在一个节点出度是奇数,那么连接根节点和奇数节点,情况变成根节点出入度都是奇数,然后按照 1. 操作即可。
3. 根节点出度是偶数,入度是奇数,存在一个节点出度是奇数,那么直接连接一条从根节点到奇数节点的非树边即可。
注意不会出现根节点出入度都是奇数并且存在一个节点出度是奇数,因为图出入度之和一定是偶数。
------------
### [[AGC024D] Isomorphism Freak](https://www.luogu.com.cn/problem/AT_agc024_d)
有意思的题目,考虑把树的直径找出来,那么如果两个点关于中心对称,那么一定存在一种加点方式可以让他们为根的时候树是同构的,即以中心为根的树,深度一样的点一定存在一种方法同构。方法就是让同深度的点的子树都相同。
那么答案就是以中心为根节点的时候的最大深度。(如果中心有两个的话两节点深度都为 $1$。)
考虑如何同时让叶子数量尽可能的小,由于上面说过了,最好的方案就是让所有同深度的节点的子树都相同。所以我们对于深度 $i$ 的节点,他的儿子数一定是深度为 $i$ 的节点中儿子数量最多的节点。
那么答案就是所有深度的最大孩子数相乘。
但是这不全面,因为如果你本来直径长度为奇数,你可以再让直径长度加一变成偶数,这时同构数量不会变化,但是叶子数量是会变化的。
这里直接枚举一个出点也作为深度为 $1$ 的根就好。
### [[AGC029E] Wandering TKHS](https://www.luogu.com.cn/problem/AT_agc029_e)
我们让原树按照 $1$ 为根节点。
把点从大到小加入到树中,对于当前 $x$ 来说,他的点集和他的父亲 $y$ 的点集有一部分相同,所有属于 $y$ 的点集,也一定属于 $x$ 的点集,并且 $x$ 多出来的一部分一定是在他的子树内。
考虑具体哪些点是 $x$ 多出来的部分,我们再 $x$ 的子树内广搜,遇到小于 $y$ 到跟路径上最大值 $z$ 的点就加入,那么这部分就是 $x$ 集合多出来的点。
对于在 $x$ 子树内的节点,它的答案和 $x$ 有重合部分,但是会比 $x$ 多,多出来的部分就是这个节点所在的 $x$ 某一个孩子的子树大小(剖去已经加入过的比 $x$ 大的节点的子树)。
这部分我们可以直接求出来,因为只要在 $x$ 的同一个孩子的子树内,那么答案一定一样。
做完之后我们把 $x$ 的子树从树中删除,因为剩下的点不可能进入这里。
最后处理出来所有的答案之后再对全树进行一遍更新即可。
### [Construct a tree](https://www.luogu.com.cn/problem/CF1098C)
整体分成两部分,判断和方案。
首先我们把子树大小和转化成为每个节点的深度和。
判断还是比较简单的,首先我们二分一个分支系数 $k$ (显然具有可二分性)
那么这种情况下,一个树的最小权值是形如下的方式。
第一层 $k^0$ 个点,第二层 $k^1$ 个点 $\cdots
最大的贡献是
贡献是 1+2+3\cdots n-1+n
我们来证明结论,只要 s 在 [\min,\max] 的区间内即可。
我们尝试从最小一步一步变成最大:
还是以这张图为原型,我们取 1-2-4-8 为主路径。
每次操作可以视作将一个节点的深度增加 1 ,并且由于没有深度限制,所以一定存在这样一种方案。
比如我们可以把 9 接到 8 的下方,以此类推,每次把一个节点深度下调 1 即可。
那么最后就会成为一条链子的情况。
所以在 [\min,\max] 里的所有数都能取到,问题在于如何输出方案。
一步一步前进肯定是不行的,我们考虑如下的方法。
每次选择深度最大并且不在主路径的节点,把它接到主路径上。
考虑这样的增长速度,容易发现,大概顺序是第一次增长 1 ,第二次增长 2 ,这样的速度(中途可能会出现增长速度增加 2 的情况,因为原本深度最大的节点用完了,不过不影响)。
等到某次这样的增长即将超过我们的答案的时候,我们就暂停。
考虑下一次增长权值为 x 会超过 s ,那么我们就不挪动到主路径的底部了,而是挪到主路径上的某一个孩子上,那么这样增加的权值可以在 [0,x] 之间。
[ARC095F] Permutation Tree
考虑已经加入了前 i 个数,那么现在加入第 i+1 个数,有两种情况:
自己不放置在最右侧,那么 i+1 的父亲是最右侧的节点,并且自身一定是一个叶子,因为最右侧的节点比 i+1 坐标大并且小于 i+1 。
自身放置在右侧,那么 i+1 的父亲是除了他以外的最右侧的点。
因此我们发现,如果一个树可以被构建出来,那么一定存在以某一个节点为根,树上的没一个节点满足他的所有孩子中至多只有一个节点不是叶子。
容易发现,这样的树就是“毛毛虫”。
判断做完了,考虑最小的前提。
毛毛虫的根一共就有两种情况:分别是直径的两头,因为其他节点不是毛毛虫或者一定不如这两个优。
考虑构建形式,加入当前的 i 的父亲往上的树合这些节点的叶子孩子已经建好了,那么需要插入当前节点和当前节点的叶子孩子。
一定形如 fa_i,i+1,i+2,i 这样的形式。
这样的话 i+1,i+2 的父亲是 i 并且字典序最小,然后 i 的非叶子孩子放在 i 的后面继续即可。
那么两个方案分别跑一遍取最优即可。
Power Tree
天才题。
将选择一个节点变成选择一个 \text{dfn} 区间,对区间进行区间 +- 。
考虑转化为差分数组上的操作,那么对于区间 [l,r] 的操作,对于差分数组来说是 w_l+x,w_{r+1}-x
相当于我们可以把 w_l 的权值运输到 w_{r+1} 。
由于我们希望所有叶子节点的权值都是 0 ,即除了 w_{n+1} 其他的权值都为 0 。
那么对于一个区间操作,我们可以认为 l\to r+1 链接了一条边,那么满足条件就可以等价于每个节点都有一条能通向 n+1 的路径,这样的话所有的 w_i 的权值就可以顺着路径搬到 w_{n+1} 了。
那就相当于我们要找到一棵根向树,又因为我们加入的边都是向右方向的,所以直接跑最小生成树即可。
Down Below
看到这道题目还以为是和生成树有关,但是本题最大的难点其实在于 u\to v 走完的时候我们不能立马进行 v\to u 。
直接算最小是困难的,我们不妨套路的先二分转判定性问题。
显然,对于已经确定初始状态的情况,我们只需要每次随便找一个合法路径走一遍,将 b_i 加到我们的权值里,最后只要能跑完所有节点就是合法的。
我们维护一个当前能走到的点集(显然点集是一个连通块),那么我们能扩展出去的合法路径有两种情况。
(下图中黄色为能走到的点集,红色为一个合法路径。)
没有成环
上图是比较简单的情况,我们扩展的合法方案是一条简单路径,对于如上情况,我们可以直接让红色路径上的点加入点集中,然后更新权值。
成环了
这种情况有些麻烦,按照题目要求我们依然可以将环上的四个节点更新到点集中。
如果我们存在一种方式可以进行如上更新,那么我们就可以完成题目。
但是我们这样更新会存在一个问题。
如图,我第一次更新会更新红色路径
第二次更新会更新蓝色路径,但是如果我们真的按照顺序更新,一旦我们处理完红色路径回到黄色点,那么由于我们不能立马走回头路,实际上我们没法继续处理蓝色方案的。
因此我们实际上不是返回黄色节点,而是假装我们返回了,但是实际上我们可以调整顺序使得对于方案之间存在合法的走法将两个方案走完。
比如上图中我们可以走到距离黄色节点最近的节点就不再返回了,而是直接进行蓝色方案。
那么现在问题就在于如何找出这两种方案。
不妨找一种简单的方法判断出如上的方案。
考虑 \text{dfs} ,我们每经过一个没在点集中的节点时,记录他的 fr 前驱,然后将 W\to W+b_i ,并且尝试遍历他的所有出边。当其出边遍历完之后,我们再将 W\to W-b_i 。
当一个节点被遍历时,若其 fr 有值,那就说明我们可以形成上述的情况 2 ,即存在一个环形可以走。
当一个节点的出边能到达一个在点集中的节点并且此节点不是 fr 时,那就说明形成了上述情况 1 ,即存在一个路径可以走。
考虑如何更新答案最简单,我们不妨将满足两种情况的节点记为 pos ,当 pos 出现后,立刻停止所有 \text{dfs} ,然后我们将 pos,fr_{pos},fr_{fr_{pos}} 等全部更新进入答案之中,考虑这样做的正确性。
显然,对于情况一没有任何问题,因为他本来就是一个路径,考虑情况二,我们如此操作会将环的一个节点并入到点集中,而环的部分完全没有考虑,但是不妨考虑下一次更新,一定会存在一条经过所有环上节点的新路径,其满足情况一。
那么我们可以在两次更新的情况下完成这个情况二。
因此代码非常简单。
对了,实际上应该处理一下重边问题,但是似乎原题并没有卡,因此无伤大雅。
P6137 [IOI2012] 理想城
之前徐老师给过,考虑曼哈顿距离可以分成 x,y 坐标分别算贡献。
考虑将 x 相同,并且 y 相邻的视作同一个节点,他们在 x 坐标的贡献完全相同。
这时原图的连通块就变成了若干节点,并且图是一棵树,此时的距离就可以通过 \text{dp} 直接算出来了。
Remove Bridges
首先我们不妨转化一下题意,首先树上每个边都是割边,一旦我们连接了两节点 x,y ,那么对应的树上路径 x\to y 的所有边都会变化为非割边。
所以我们每次操作本质上是选定树上一条路径覆盖。
考虑合法状态本质,也就是说对于一条边,如果他没被覆盖,那么他的子树内也不能有覆盖边。
因此我们的状态本质是一个连通块,并且这个连通块一定包含根。
现在考虑如何用 k 次覆盖路径达到一个合法且最大的状态。
路径覆盖过于麻烦,所以我们不妨转化为形成一个连通块,其有 x 个叶子(度数为 1 的节点)。显然 x 个叶子的连通块可以用 \left\lceil\dfrac{x}{2}\right\rceil 次路径覆盖形成。
现在问题转化为对于每一个 x 求出恰好有 x 个叶子并且包含 1 的连通块最大是多少。
这玩意看着就像可以贪心的搞,这里我们不妨证明一下。
考虑 k=i 的情况,我们已经得到了一个最大的连通块。
如图,假定 k=1 ,显然我们 k=1 的最大连通块为 \text{\color{red}红色} 路径。
考虑对于每一个节点 i ,我们维护出其子树内部最深(之一)的叶子是谁称之为 son_i 。
每次,我们将和当前连通块相邻的节点 i 放进集合 S 中。
我们将 S 集合按照 \text{dep}_i-\text{dep}_{son_i} 从大到小排序。每次将权值最大的 i 提取出来,将 son_i\sim i 这条路径上的节点加入到连通块里,并且更新 S 集合。
考虑证明其为什么是对的,首先,对于一个已经加入集合的节点,在没有选择它的时候,不管外界作何选择,绝对不会影响其答案。
对于一次选择 i\to son_i ,我们的贡献理论上应该是 w_i ,对于因为这次选择而更新出的节点 x ,显然 w_x<w_i 如若不然,那么就违背了 son_i 是 i 子树内最深的节点。
因此我们纵观整个流程,每次取出契合中最大的权值,然后会新形成一些比其小的权值塞入集合中。因此无需策略,只需要无脑的选择最大即可更新出答案。
Sum of Prefix Sums
考虑如何合并两个路径,算出新路径的答案,不难发现可以转化为一次函数问题。
考虑点分治,然后插入一个全局线段,复杂度 n\log^2 n 。
Li Hua and Path
一个不错的题目,重新引发了我对重构树的思考。
多的不说,先看题目。
题目是让我们求解两类点对。
我们称 A 集合中的点对,满足题目的 case1(A 性质)。
$C=A\cap B$,即同时满足 `case1` `case2` 的点对。
那么答案就是 $|A|+|B|-2\times |C|$。
先不考虑加点操作,我们只考虑一棵普通的树。
由于题目让求的类似于瓶颈路,所以我们自然的想到 $\text{Kruskal}$ 及其重构树。
我们考虑如何求解 $|A|$($|B|$ 同理即可)。
因此本质上,我们需要对于每个节点 $x$,求出在经过不小于 $x$ 节点的情况下,能到达的点集。
由于是 $\text{Kruskal}$ 算法,我们要考虑边权是什么,考虑一条 $x\leftrightarrow y$ 的边,不管我们是从 $x\to y$,亦或是 $y\to x$,我们经过的最小节点一定是 $\min (x,y)$,因此我们自然可以将 $x\leftrightarrow y$ 的边权定为 $\min (x,y)$。
那么我们按照边权从大到小建出 $\text{Kruskal}$ 重构树,那么对于一个节点 $x$,其能到达的节点就是不断暴力向上跳父亲,直至最高的,权值为 $x$ 的节点,那么其子树内的所有节点 $x$ 都能在作为最小值的情况下到达。
其实到这里就差不多了,继续转头去处理 $|C|$ 即可,但是我发现我们这一切的前提都在权值为 $x$ 的节点在重构树上都是一个联通快的情况下。
这其实是非常好理解的,因为重构树新建节点本质是边,而边权相等的边会紧挨着依次加入,因此形成的权值为 $x$ (包括 $x$ 本身对应的节点)他们一定是联通的。
这时我又进一步的思考,可不可以将树上,权值相同的节点缩起来?
举个例子
对于原树:
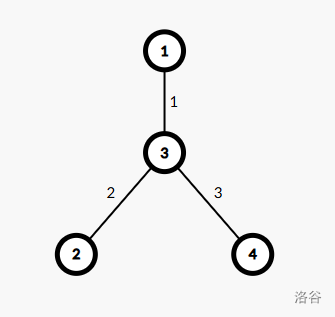
我们建出的朴素重构树为:

我们不妨将点缩起来,即 $w=1,1|w=2,w|w=3,3|4$ 一共组点,并且依然维护连边性。
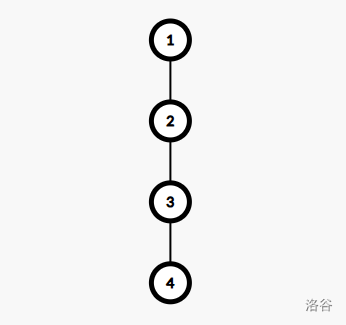
其中 $1$ 为根节点,那么对于图中的任何一个节点 $i$,其子树内所有节点都可以通过走不小于 $i$ 的点到达。
这样我们就构造出了一棵 $n$ 个节点的树,并且完美的满足 $A$ 性质。
那么点对总数就是每个节点的子树 $\text{size}$ 之和。
同理我们继续求出 $|B|$ 即可。
为了方便,我们称满足 $A$ 性质的树为 $A$ 树,同理为 $B$ 树。
现在考虑如何求出 $|C|$,我们不妨枚举一个节点 $i$,考虑对于他来说有多少条以其为大端点的路径且满足性质 $C$。
这是一个偏序问题,根据上述定义我们可知,对于一个合法节点 $j$ 其要满足在 $B$ 树上是 $i$ 的孩子,且 $A$ 树上是 $i$ 的祖先。
处理这个也很简单和套路,我们不妨求出每个节点在 $B$ 树上的 $\text{dfn}$ 序,然后在 $A$ 树上 $\text{dfs}$,每次将访问新节点 $i$ 时将 $\text{dfn}_{i}$ 位置 $+1$,离开时将 $\text{dfn}_i$ 位置 $-1$。这样我们就可以保证仅在 $A$ 树上为 $i$ 祖先的节点有贡献,然后查询 $B$ 树上的 $i$ 子树总和即可。
轻松加愉快就解决了!
但是别急,我们还要处理添加新节点那。
考虑添加一个新节点 $n+i$,容易发现,他在 $B$ 树上一定为根,这是一个很好的性质,因此他对 $|B|$ 的贡献就是 $n+i$,而在 $A$ 树上,截止目前,他一定是一个叶子,因此对 $|A|$ 的贡献为其深度。
考虑 $|C|$ 的贡献,由于在 $B
树上,它当前是根,对于任何一个其在 A 树上的祖先,也一定满足 B 树上的限制,因此对 |C| 的贡献一定为祖先数量,也就是其深度。