NOIP2024 解题报告
Graphcity
·
·
生活·游记
省流:没有上 400pts 的自行反思
总结:峰值难度不如 CSP2024,但整体难度比 CSP2024 和 NOIP2023 要难一些。
这套题最大的困难在于 时间。考察的都是基本功,既有 T4 这种比较朴素但是略复杂的数据结构,也有 T3 这样需要花一些心思去大力分类讨论的题目。这体现出了平时练习时需要重视基本功的锻炼。
Edit
贪心,从左往右能配对就配对,不配对就摆烂。O(n)。
这个贪心的正确性在于:
- 这是第一题。
我是位置学大师
- 相信大家都会调整法吧?
反正我不会
参考用时:10min
#include<bits/stdc++.h>
#define For(i,a,b) for(int i=(a);i<=(b);++i)
#define Rof(i,a,b) for(int i=(a);i>=(b);--i)
using namespace std;
const int Maxn=2e5;
int T,n,A[Maxn+5],B[Maxn+5],a[Maxn+5][2],b[Maxn+5][2],c[Maxn+5],d[Maxn+5];
inline void Solve()
{
scanf("%d",&n);
For(i,1,n) scanf("%1d",&A[i]);
For(i,1,n) scanf("%1d",&B[i]);
For(i,1,n) scanf("%1d",&c[i]);
For(i,1,n) scanf("%1d",&d[i]);
for(int i=1,j=Maxn;i<=n;++i) {if(c[i]) j=min(j,i),a[j][A[i]]++; else j=Maxn;}
for(int i=1,j=Maxn;i<=n;++i) {if(d[i]) j=min(j,i),b[j][B[i]]++; else j=Maxn;}
int xa[2],xb[2],ans=0;
xa[0]=xa[1]=xb[0]=xb[1]=0;
For(i,1,n)
{
// cerr<<xa[0]<<' '<<xa[1]<<' '<<xb[0]<<' '<<xb[1]<<endl;
if(c[i]) For(j,0,1) xa[j]+=a[i][j];
if(d[i]) For(j,0,1) xb[j]+=b[i][j];
if(!c[i] && !d[i]) {ans+=(A[i]==B[i]); continue;}
if(!c[i])
{
if(xb[A[i]]) xb[A[i]]--,ans++;
else xb[A[i]^1]--; continue;
}
if(!d[i])
{
if(xa[B[i]]) xa[B[i]]--,ans++;
else xa[B[i]^1]--; continue;
}
int flg=0;
For(j,0,1) if(xa[j] && xb[j] && !flg) {xa[j]--,xb[j]--,ans++,flg=1;}
For(j,0,1) if(xa[j] && xb[j^1] && !flg) {xa[j]--,xb[j^1]--,flg=1;}
}
printf("%d\n",ans);
For(i,0,n+1) A[i]=B[i]=c[i]=d[i]=0;
For(i,0,n+1) For(j,0,1) a[i][j]=b[i][j]=0;
}
int main()
{
// freopen("1.in","r",stdin);
scanf("%d",&T);
while(T--) Solve();
return 0;
}
Assign
不会的可以退役了。
如果相邻的两个点不是一条链从首连到尾,而且尾部还不一样的话,那么肯定合法的。O(n\log V)。
参考用时:10min
#include<bits/stdc++.h>
#define For(i,a,b) for(int i=(a);i<=(b);++i)
#define Rof(i,a,b) for(int i=(a);i>=(b);--i)
using namespace std;
const int Maxn=2e5,Mod=1e9+7;
inline int Pow(int x,int y)
{
int res=1;
while(y)
{
if(y&1) res=1ll*res*x%Mod;
x=1ll*x*x%Mod,y>>=1;
}
return res;
}
int T,n,m,K,ans=1;
pair<int,int> h[Maxn+5];
inline int F(int x) {return Pow(K,x*2);}
inline void Solve()
{
cin>>n>>m>>K; ans=1;
For(i,1,m) cin>>h[i].first>>h[i].second;
sort(h+1,h+m+1);
For(i,1,m-1) if(h[i].first==h[i+1].first && h[i].second!=h[i+1].second)
{cout<<0<<endl; return;}
ans=1ll*F(h[1].first-1)*F(n-h[m].first)%Mod;
For(i,1,m-1) if(h[i].first!=h[i+1].first)
{
int s1=1ll*Pow(K,h[i+1].first-h[i].first-1)*(K-1)%Mod;
int s2=F(h[i+1].first-h[i].first);
ans=1ll*ans*(s2-s1+Mod)%Mod;
}
cout<<ans<<endl;
}
int main()
{
// freopen("1.in","r",stdin);
// freopen("1.out","w",stdout);
cin>>T;
while(T--) Solve();
return 0;
}
Traverse
本场最难题。需要耐心和一些观察力。
21 世纪最重要的品质——淡定。
如果把边看作方点,点看作圆点的话,我们实际上求的就是一棵仙人掌对应圆方树的生成树个数。
我们可以得到一些性质:
1. 对于每个圆点,其相邻的所有方点用一条链连接。
2. 这是一棵二叉树。
3. 如果遇到一个方点有三叉的情况,那么根结点(关键方点)肯定不在它连了其中两个叉的圆点的子树中。
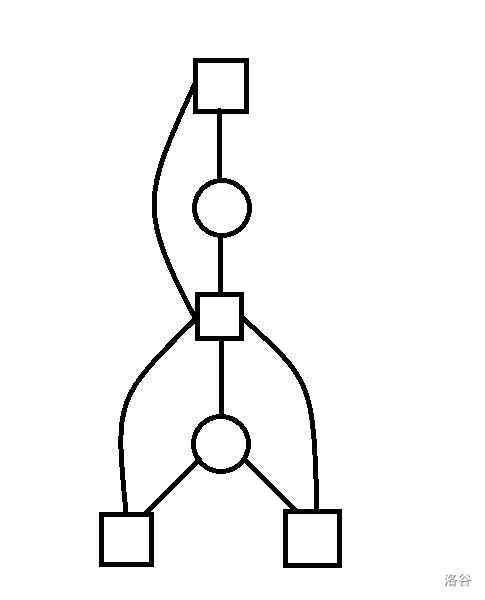
我们把上面的情况称为「monster」~~(非常可怕的情况)~~
注意到所有的 monster 应该在一条链上,否则不可能存在合法的根结点。
设 $f_{i,0/1/2}$ 表示 $i$ 这个圆点的子树中(还要包括它的父亲方点)的方案数。
0. 没有 monster 情况,暂时还没有合法的根结点。
1. 没有 monster 情况,存在合法的根结点。
2. 存在 monster 情况。这意味着根结点必须在这棵子树中。
对于 0/1 之间的转移还是比较简单的。如果要是 1 的话,你就得先找到一个为 1 的儿子,然后这个儿子要在这个结点对应链的一端。剩下的都是 0 的情况。
然后是从 1 儿子转移到 2 的情况。这意味着当前结点必须出现一个 monster(也就是父亲方点要连接两条边),而且 1 儿子仍然要在这条链的一端。注意去重。
从 2 转移到 2 类似。总时间复杂度 $O(n\log V)$(包括快速幂)。
参考用时:思考 30min + 实现 30min + 调题 30min
```cpp
#include<bits/stdc++.h>
#define For(i,a,b) for(int i=(a);i<=(b);++i)
#define Rof(i,a,b) for(int i=(a);i>=(b);--i)
using namespace std;
const int Maxn=2e5,Mod=1e9+7;
inline int Pow(int x,int y)
{
int res=1;
while(y)
{
if(y&1) res=1ll*res*x%Mod;
x=1ll*x*x%Mod,y>>=1;
}
return res;
}
inline int Inv(int x) {return (x==0)?1:Pow(x,Mod-2);}
int ID,T,n,m,rt,A[Maxn+5],B[Maxn+5],fa[Maxn+5];
int chk[Maxn+5],f[Maxn+5][3],fac[Maxn+5];
int pr[Maxn+5],sf[Maxn+5];
vector<int> v[Maxn+5];
inline void Clear()
{
For(i,1,n) chk[i]=fa[i]=f[i][0]=f[i][1]=f[i][2]=0;
For(i,1,n) vector<int>().swap(v[i]);
}
inline void dfs0(int x,int f)
{fa[x]=f; for(auto y:v[x]) if(y!=f) dfs0(y,x);}
inline void dfs(int x)
{
// Case 1: root not sure
f[x][0]=1; for(auto y:v[x]) if(y!=fa[x]) dfs(y);
int cur=1; for(auto y:v[x]) if(y!=fa[x]) pr[y]=cur,cur=1ll*cur*(f[y][0]+f[y][1])%Mod;
reverse(v[x].begin(),v[x].end()),cur=1;
for(auto y:v[x]) if(y!=fa[x]) sf[y]=cur,cur=1ll*cur*(f[y][0]+f[y][1])%Mod;
reverse(v[x].begin(),v[x].end());
for(auto y:v[x]) if(y!=fa[x]) f[x][0]=1ll*f[x][0]*(f[y][0]+f[y][1])%Mod;
if(x==rt) return;
int son=v[x].size()-1; f[x][0]=1ll*f[x][0]*fac[son]%Mod;
for(auto y:v[x]) if(y!=fa[x])
{
int res=1ll*(f[y][1]+chk[y]*f[y][0])%Mod*pr[y]%Mod*sf[y]%Mod;
f[x][1]=(f[x][1]+1ll*res*fac[son-1])%Mod;
}
f[x][0]=(f[x][0]-f[x][1]+Mod)%Mod;
// Case 2: New Sure Root
if(son>1)
{
for(auto y:v[x]) if(y!=fa[x])
{
int res=1ll*(f[y][1]+chk[y]*f[y][0])%Mod*pr[y]%Mod*sf[y]%Mod;
f[x][2]=(f[x][2]+1ll*res*(son-1)%Mod*fac[son-1])%Mod;
}
int sum=0,all=1;
for(auto y:v[x]) if(y!=fa[x]) all=1ll*all*(f[y][0]+f[y][1])%Mod;
for(auto y:v[x]) if(y!=fa[x])
{
int s=1ll*Inv((f[y][0]+f[y][1])%Mod)*(f[y][1]+chk[y]*f[y][0])%Mod;
int res=1ll*s*sum%Mod*fac[son-1]%Mod;
f[x][2]=(f[x][2]-1ll*res*all%Mod+Mod)%Mod;
sum=(sum+s)%Mod;
}
}
// Case 3: Sure Root
for(auto y:v[x]) if(y!=fa[x])
{
int res=1ll*f[y][2]*pr[y]%Mod*sf[y]%Mod;
f[x][2]=(f[x][2]+1ll*res*(fac[son-1]+1ll*(son-1)*fac[son-1]%Mod))%Mod;
}
// cerr<<"kk "<<x<<' '<<f[x][0]<<' '<<f[x][1]<<' '<<f[x][2]<<' '<<endl;
}
inline void Solve()
{
cin>>n>>m;
For(i,1,n-1) cin>>A[i]>>B[i],v[A[i]].push_back(B[i]),v[B[i]].push_back(A[i]);
For(i,1,n) if(v[i].size()==1) {rt=i; break;}
dfs0(rt,0);
For(i,1,m)
{
int p; cin>>p; int a=A[p],b=B[p];
if(fa[a]==b) swap(a,b); chk[b]=1;
}
dfs(rt); int p=v[rt].front();
int ans=(f[p][1]+chk[p]*f[p][0])%Mod;
ans=(ans+f[p][2])%Mod;
// cerr<<rt<<' '<<f[p][0]<<' '<<f[p][1]<<' '<<f[p][2]<<endl;
cout<<ans<<endl;
Clear();
}
int main()
{
// freopen("1.in","r",stdin);
// freopen("1.out","w",stdout);
cin>>ID>>T; fac[0]=1;
For(i,1,Maxn) fac[i]=1ll*fac[i-1]*i%Mod;
while(T--) Solve();
return 0;
}
```
## Query
锅砸简单。
考场上一定要判断好题目的难易顺序。
看到 $n,q\le 5\times 10^5$ 就会立马发现这件事不太简单,它居然可以做到 1log!
考虑用类似 Kruskal 重构树的方式建立一棵 LCA 树:每个结点代表一个区间 $[l,r]$ 和一个结点 $p$,表示 $LCA^*(l,r)=p$,且 $LCA^*(l-1,r)$ 和 $LCA^*(l,r+1)\not=p$。
一开始我们构建所有的叶子结点 $([i,i],i)$,然后把相邻两个叶子的 LCA 代表的结点放进堆里面,堆按照结点深度从大往小排序。每次从堆中取出一个元素时,表示新建立一个结点。然后把它和它左右两个邻居结点的 LCA 再次放入堆中,以此类推,直到构建出 $([1,n],1)$ 为止。这一步是 $O(n\log n)$ 的。
求出这棵树有什么用呢?注意到,所有的有效区间就是这棵树上结点所代表的区间,只有 $O(n)$ 个!如果一个有效区间与询问区间的交长度 $\ge k$,那么它就可以贡献到询问里面。
我们按照有效区间 $[l,r]$ 和询问区间 $[p,q]$ 的位置关系分类讨论:
1. $l\ge p$,此时只需要 $r-l+1\ge k$,$l\in[p,q-k+1]$ 即可。
2. $r\le q$,此时只需要 $r-l+1\ge k$,$r\in [p+k-1,q]$ 即可。
3. $[p,q]\subseteq[l,r]$,必然合法。
注意到 $[l,r]\subseteq[p,q]$ 的情况必然包含于前面两种情况之内,不需要再讨论。
这是二维偏序问题,简单的扫描线即可,线段树可以做到 $O(n\log n)$。代码非常好写。
参考用时:1h
```cpp
#include<bits/stdc++.h>
#define For(i,a,b) for(int i=(a);i<=(b);++i)
#define Rof(i,a,b) for(int i=(a);i>=(b);--i)
using namespace std;
const int Maxn=1e6;
int n,m,ans[Maxn+5],L[Maxn+5],R[Maxn+5],K[Maxn+5];
int hl[Maxn+5],hr[Maxn+5],h[Maxn+5],dep[Maxn+5],q;
int fa[Maxn+5],st[Maxn+5][20],dfn[Maxn+5],cur;
vector<int> v[Maxn+5];
struct DSU
{
int fa[Maxn+5];
inline int Find(int x) {return fa[x]==x?x:fa[x]=Find(fa[x]);}
} D;
inline void dfs0(int x,int f)
{
fa[x]=f,dfn[x]=++cur,st[cur][0]=f,dep[x]=dep[f]+1;
for(auto y:v[x]) if(y!=f) dfs0(y,x);
}
inline int GetID(int x,int y) {return dfn[x]<dfn[y]?x:y;}
inline int LCA(int x,int y)
{
if(x==y) return x; if((x=dfn[x])>(y=dfn[y])) swap(x,y);
int len=__lg(y-x++); return GetID(st[x][len],st[y-(1<<len)+1][len]);
}
struct Data{int x,y,k;};
inline bool operator<(Data a,Data b) {return dep[a.k]<dep[b.k];}
inline void BuildSeg()
{
priority_queue<Data> q;
For(i,1,n-1) q.push(Data{i,i+1,LCA(i,i+1)});
while(!q.empty())
{
int x=q.top().x,y=q.top().y,k=q.top().k; q.pop();
if(x!=D.Find(x) || y!=D.Find(y)) continue;
int p=++m,w; hl[p]=hl[x],hr[p]=hr[y],h[p]=k; D.fa[x]=D.fa[y]=p;
if(hl[p]>1) w=D.Find(hl[p]-1),q.push(Data{w,p,LCA(h[w],h[p])});
if(hr[p]<n) w=D.Find(hr[p]+1),q.push(Data{p,w,LCA(h[p],h[w])});
}
}
int len[Maxn+5],im[Maxn+5],iq[Maxn+5];
struct SegTree
{
int t[Maxn*4+5];
#define ls(x) (x<<1)
#define rs(x) (x<<1|1)
inline void push_up(int p) {t[p]=max(t[ls(p)],t[rs(p)]);}
inline void Build(int l,int r,int p)
{
t[p]=0; if(l==r) return;
int mid=(l+r)>>1; Build(l,mid,ls(p)),Build(mid+1,r,rs(p));
}
inline void Insert(int l,int r,int p,int pos,int k)
{
if(l==r) {t[p]=max(t[p],k); return;} int mid=(l+r)>>1;
if(pos<=mid) Insert(l,mid,ls(p),pos,k);
else Insert(mid+1,r,rs(p),pos,k); push_up(p);
}
inline int Count(int nl,int nr,int l,int r,int p)
{
if(l<=nl && nr<=r) return t[p];
int mid=(nl+nr)>>1,res=0;
if(l<=mid) res=max(res,Count(nl,mid,l,r,ls(p)));
if(r>mid) res=max(res,Count(mid+1,nr,l,r,rs(p)));
return res;
}
} T;
// Caution: hl/hr, L/R
int main()
{
// freopen("1.in","r",stdin);
// freopen("1.out","w",stdout);
ios::sync_with_stdio(false);
cin>>n;
For(i,1,n-1) {int a,b; cin>>a>>b; v[a].push_back(b),v[b].push_back(a);}
dfs0(1,0); For(j,1,19) for(int i=1;i+(1<<j)-1<=n;++i)
st[i][j]=GetID(st[i][j-1],st[i+(1<<j-1)][j-1]);
For(i,1,n*2) D.fa[i]=i; m=n; For(i,1,n) hl[i]=hr[i]=i,h[i]=i;
BuildSeg(); cin>>q;
For(i,1,q) cin>>L[i]>>R[i]>>K[i];
// q=1,L[1]=L[4],R[1]=R[4],K[1]=K[4];
// cerr<<L[4]<<' '<<R[4]<<' '<<K[4]<<endl;
iota(im+1,im+m+1,1),iota(iq+1,iq+q+1,1);
For(i,1,m) len[i]=hr[i]-hl[i]+1;
sort(iq+1,iq+q+1,[&](int x,int y){return K[x]>K[y];});
sort(im+1,im+m+1,[&](int x,int y){return len[x]>len[y];});
T.Build(1,n,1);
for(int _=1,it=1;_<=q;++_)
{
int i=iq[_]; while(it<=m && K[i]<=len[im[it]])
{int k=im[it++]; T.Insert(1,n,1,hl[k],dep[h[k]]);}
ans[i]=max(ans[i],T.Count(1,n,L[i],R[i]-K[i]+1,1));
}
// For(i,1,m) if(min(hr[i],357)-max(hl[i],2)+1>=223)
// cerr<<i<<' '<<hl[i]<<' '<<hr[i]<<' '<<h[i]<<' '<<dep[h[i]]<<endl;
T.Build(1,n,1);
for(int _=1,it=1;_<=q;++_)
{
int i=iq[_]; while(it<=m && K[i]<=len[im[it]])
{int k=im[it++]; T.Insert(1,n,1,hr[k],dep[h[k]]);}
ans[i]=max(ans[i],T.Count(1,n,L[i]+K[i]-1,R[i],1));
}
sort(iq+1,iq+q+1,[&](int x,int y){return L[x]<L[y];});
sort(im+1,im+m+1,[&](int x,int y){return hl[x]<hl[y];});
T.Build(1,n,1);
for(int _=1,it=1;_<=q;++_)
{
int i=iq[_]; while(it<=m && hl[im[it]]<=L[i])
{int k=im[it++]; T.Insert(1,n,1,hr[k],dep[h[k]]);}
ans[i]=max(ans[i],T.Count(1,n,R[i],n,1));
}
For(i,1,q) cout<<ans[i]<<'\n';
return 0;
}
```