浅谈二分图:从入门到入坟
MatchaNeko_nya
·
·
个人记录
0x00 引言
二分图,一种图论中相对而言较为简单的图种,但似乎没有什么人注意,笔者此篇文章的目的就是介绍这种图以及相关算法。
0x10 二分图是什么?
二分图,又称二部图,英文名叫 Bipartite graph。
二分图是什么?节点由两个集合组成,且两个集合内部没有边的图。
换言之,存在一种方案,将节点划分成满足以上性质的两个集合。
——出自oi-wiki
如上所示,二分图的意义和名字一样十分形象。用通俗的语言来讲,就是说把一个图里的所有点划分成两个集合,且每条边的两个端点都不在同一集合。这就是二分图。
这里需要注意二分图的一个特殊性质——二分图不存在长度为奇数的环。
如果读者无法理解,可以按以下思路想:
-
若有长度为奇数的环,则可以将这个环变成一个铅笔头状的环。
-
对“铅笔头”染色,显而易见地,“铅笔头”左右两个对称点颜色相等。
-
到达底部时,由 2. 可知底部两边点颜色相等,但与二分图定义冲突,因此二分图不存在长度为奇数的环。
上述步骤如下图所示:
0x20 二分图常见题型
0x21 判断是否为二分图
注意二分图的定义,我们可以把二分图的点集分成两个子点集 G,E,并且任意两个之间有边连接的点一定不属于同一个子点集。
那么我们可以对一个图在深搜的过程中进行染色,如果遇到冲突情况,那么这个图一定不是二分图。
需要注意:二分图不一定是连通图,所以需要对一个图的每一个区块(即构成一个非连通图的多个连通图)进行单独的染色。
完成练习:
\color{#FFC116}\textbf{P1330 封锁阳光大学}
\color{#52C41A}\textbf{P1525 [NOIP2010 提高组] 关押罪犯}
0x22 二分图最大匹配
读者首先需要理解一些术语:
左部点:二分图的两个子点集中的一个集合。
右部点:二分图中除了左部点的另外一个集合。
匹配:任意两条边都没有公共端点的边的集合。
最大匹配:在所有匹配方案中,所含边数最多的匹配方案。
完备匹配:如果一个匹配中,图中的每个顶点都和图中某条边相关联,此匹配为完备匹配,又称完全匹配。
完美匹配:如果一个匹配中,包含了图中的所有顶点,则此匹配为完美匹配。
匹配边:对于任意一个匹配 S (边集)中属于 S 的边。
匹配点:匹配边的端点。
增广路:一条连接两个非匹配点的路径,且匹配边和非匹配边在此条路径上交替出现。
请读者注意增广路的几个性质:
-
增广路的长度一定为奇数。
-
路径上编号为奇数的边是非匹配边,编号为偶数的是匹配边。
正因为以上性质,所以如果将一条增广路的所有边的状态取反(即匹配边变为非匹配边,反之亦然),得到的新的匹配 S' (边集)仍然为一组匹配,并且匹配边数增加了 1,进一步得到推论:
二分图的一组匹配 S 是最大匹配,当且仅当图中不存在 S 的增广路。
$\text{A1:}$ 因为由增广路的性质可知,非匹配边的数量一定是匹配边的数量 $+1$。
$\text{Q2:}$ 为什么没有 $S$ 的增广路,$S$ 就是最大匹配?
$\text{A2:}$ 因为如果有 $S$ 的增广路,则匹配边数必然可以增加(由 $\text{A1}$ 可知)。
二分图最大匹配,通常使用匈牙利算法(The Hungarian Method,又称增广路算法)来解决。
#### 匈牙利算法(增广路算法):
匈牙利算法的主要过程有三步:
1. 设一个边集 $S=\emptyset$,即所有边都是非匹配边;
2. 寻找增广路 $P$,把路径上所有边的匹配状态取反,得到一个更大的匹配 $S'$。
3. 重复第 2. 步,直到无法找到增广路。
可见,匈牙利算法的关键在于如何找到增广路。匈牙利算法依次尝试给各个左部点 $x$ 寻找匹配的右部点 $y$。若 $(x,y)$ 可以匹配,则至少满足以下两个条件之一:
1. $y$ 为非匹配点。($x\sim y$ 构成长度为 $1$ 的增广路)。
2. 原来与 $y$ 匹配的点 $x'$ 还可以找到另外一个可匹配点 $y'$ 与之匹配。($x\sim y\sim x'\sim y'$ 构成增广路)。
匈牙利算法通常使用深度优先搜索的框架,从 $x$ 递归出发寻找增广路。如果找到,那么在回溯时将路径上的匹配状态取反。此外,还可以用一个 bool 类型的时间戳数组,防止重复访问。
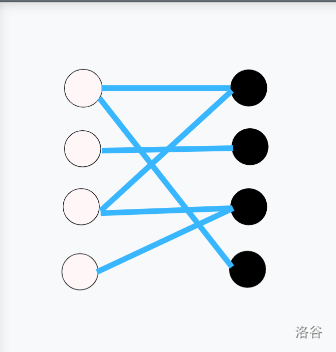
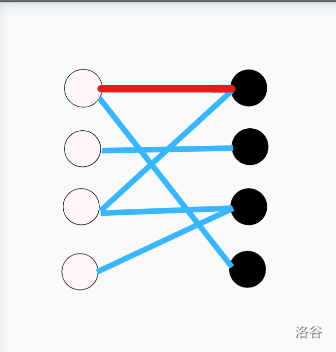
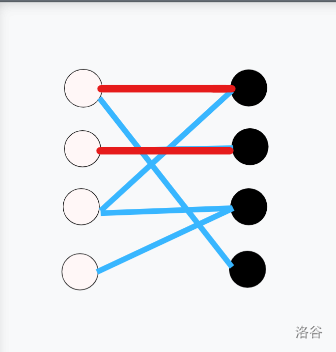
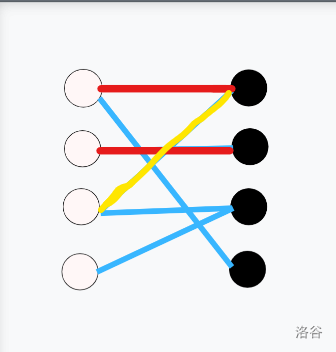
以下展示了一次匈牙利算法的过程(蓝色边为非匹配边,红色边为匹配边,黄色边为尝试匹配失败):
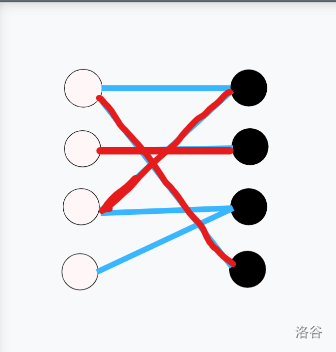
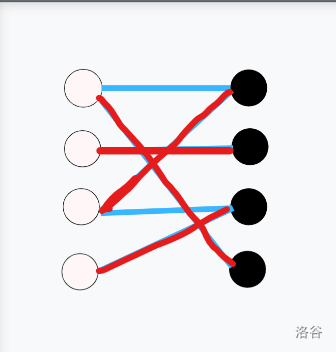
```cpp
bool dfs(int x)
{
for (auto y : vec[x])
{
if (!vis[y])
{
vis[y] = 1;
if (!match[y] || dfs(match[y]))
{
match[y] = x;
return true;
}
}
}
return false;
}
int main()
{
for (int i = 1; i <= n; i++)
{
memset(vis, 0, sizeof(vis));
if (dfs(i))
ans++;
}
cout << ans;
return 0;
}
```
显然,使用匈牙利算法(增广路算法)求二分图最大匹配的时间复杂度为 $\Theta(nm)$。
**众所周知,图论问题,建模是很重要的。**
所以下面用一道例题来讲解如何构造出二分图模型,再使用匈牙利算法求最大匹配。
给定一个 $n\times m$ 的棋盘,上面有一些格子禁止放置棋子,问棋盘上最多能放几个车?
注意到:棋盘上每一行,每一列,**最多**都只能放一个车,联想到二分图最大匹配的条件——**每个节点只能和 $1$ 条匹配边相连**。那么,我们把一个车当作一条边,单独的一行作为左部点,单独的一列,作为右部点。对于任意一个**没有被禁止放置**的点 $(i,j)$,将左部点 $i$ 和 右部点 $j$ 之间建一条边。最后进行二分图最大匹配即可,时间复杂度 $\Theta((n+m)nm)$。
完成练习:
> [$\color{#52C41A}\textbf{P3386 【模板】二分图最大匹配 }$](/problem/P3386)
>
> [$\color{#3498db}\textbf{P2071 座位安排}$](https://www.luogu.com.cn/problem/P2071)
>
> [$\color{#3498db}\textbf{P2756 飞行员配对方案问题}$](https://www.luogu.com.cn/problem/P2756)
### 0x23 二分图多重匹配(选读)
给定一个含有 $n$ 个左部点,$m$ 个右部点的二分图,从中选出**尽量多**的边,使得第 $i(1\le i\le n)$ 个左部点,至多与 $l_i$ 个边相连,第 $j(1\le j\le m)$ 个右部点,至多与 $r_i$ 个边相连。
对于多重匹配,常见的有四种解决方式:
1. 将第 $i$ 个左部点拆成 $l_i$ 个左部点,第 $j$ 个右部点拆成 $r_i$ 个右部点,且拆出来的点继承原节点的所有边,跑最大匹配即可。
2. 如果 $\forall i,l_i=1$ 或 $\forall j,r_j=1$,即只有一侧是“多重”匹配,可以设左部“多重”,在匈牙利算法中让每个左部点执行 $l_i$ 次 dfs。
3. 在第 2 种方案中,也可以交换左右两部,设“右部”多重,修改匈牙利算法的实现,让右部点匹配 $r_j$ 次,超过匹配次数后,依次尝试递归当前匹配的 $r_j$ 个左部点,看是否能找到增广路。
4. 网络流,简单高效、朴实无华、十分优雅。(~~优雅,永不过时,但会过头。~~)
选择性练习:
> [$\color{#9D3DCF}\textbf{P4068 [SDOI2016]数字配对}$](https://www.luogu.com.cn/problem/P4068)
### 0x24 二分图带权最大匹配
给定一张二分图,二分图的每条边都带有一个权值。求出该二分图的一组最大匹配,使得匹配边的权值总和最大。**请读者注意,二分图带权最大匹配的前提是匹配数最大,然后再最大化匹配边的权值。**
一般情况下,二分图带权最大匹配有 $2$ 种解法:KM 算法 与 费用流。
KM 算法的实现较为简单,且在稠密图上的效率一般比费用流高。因此,本文先介绍 KM 算法。
**注意,使用 KM 算法的前提条件是“带权最大匹配必须是完备匹配”。** 为此,在下文的讨论中,皆设二分图左右两部的节点数皆为 $N$。
首先引出几个术语:
**交错树**
在匈牙利算法中,如果从某个左部节点出发寻找匹配失败,那么在 dfs 的过程中,所有访问过的节点,以及为访问这些节点而经过的边,共同构成一棵树。
这棵树的根是一个左部节点,所有叶子结点也是左部节点(因为最终匹配失败),并且树上的奇数层的边都是非匹配边,偶数层的边都是匹配边。这棵树被称作**交错树**。
**顶标**
全称“顶点标记值”。在二分图中,给第 $i(1\le i \le N)$ 个左部节点一个整数值 $A_i$。给第 $j(1\le j \le N)$ 个右部节点一个整数值 $B_j$。同时,必须满足 $\forall i,j,A_i+B_j\le w_{i,j}$,其中 $w_{i,j}$ 表示第 $i$ 个左部节点 与 第 $j$ 个右部节点之间的边权,没有边时设为负无穷。这些 $A_i,B_j$ 称为节点的**顶标**。
**相等子图**
二分图中的所有节点以及满足 $A_i+B_j=w_{i,j}$ 的边构成的子图,称为二分图的**相等子图**。
那么显而易见地可以引出一条定理:**若相等子图中存在完备匹配,则这个完备匹配就是二分图的带权最大匹配。**
----
证明:
相等子图中,完备匹配的边权之和为 $\Sigma^{N}_{i=1}(A_i+B_i)$,即所有顶标之和。
又 $\because \forall i,j,A_i+B_j \geq w_{i,j}
证毕。
---
KM 算法的基本流程如下:
1. 在满足 $A_i+B_j \geq w_{i,j}$ 的条件下,给每个节点赋一个顶标,不妨赋值 $A_i=\max\limits_{i\le j\le n} \{w_{i,j}\},B_j=0$。
2. 寻找一种合适的方法扩大相等子图的规模直至存在完备匹配。
对于一个相等子图,我们用匈牙利算法求最大匹配,若不完备,说明一定有一个左部节点匹配失败,那么就以这个节点为根,dfs 的过程中形成了一棵交错树,记作 $T$。
考虑匈牙利算法,显然出现两条结论:
1. 除了根节点外,$T$ 中的其他左部点都是**从右部点沿着匹配边**访问到的,即调用了 `hungary_dfs(match[y])`,其中 $y$ 是一个右部节点。
2. $T$ 中的所有右部点都是**从左部点沿着非匹配边**访问到的。
由于在寻找到增广路之前,我们不会改变匹配边的状态,所以只能从第 2. 条结论入手,考虑如何让左部点沿着非匹配边访问到更多的右部点。
假如我们~~通过神秘的宇宙射线力量~~把交错树 $T$ 中的所有左部节点顶标 $A_i(i\in T)$ 减少一个整数值 $\Delta$,把所有右部节点 $B_j(j\in T)$ 增加 $\Delta$,访问情况会发生怎样的变化?
显然通过上述结论第 2. 条,讨论左部点 $i$ 沿着非匹配边尝试匹配右部点 $j$ 的两种情况:
显然,左部点的访问是被动的(被右部点沿着匹配边递归访问),所以只需讨论 $i\in T$。
- $j\in T$,$A_i+B_j$ 不变,以前能访问的现在依然能访问。
- $j\not \in T$,$A_i+B_j$ 减小(因为 $A_i$ 减小,$B_j$ 不变),有可能可以访问到新的节点了。
为了保证顶标符合前提 $A_i+B_j\geq w_{i,j}$,我们就使 $\Delta=\min\limits_{i\in T,j\not\in T}\{A_i+B_j-w_{i,j}\}$。只要原图存在完备匹配,这样的边一定存在。上述方法既不会破坏前提条件,又能保证至少有一条新的边会加入相等子图,使交错树中至少一个左部点能访问的右部点数量增多。
不断重复此过程,直到每一个右部点都匹配成功,就得到了相等子图的完备匹配,即原图的带权最大匹配。具体实现时,可以使用一个数组用来更新 $\Delta$ 的值。时间复杂度为 $\Theta(n^2m)\approx\Theta(n^4)$(最坏情况下)。
实测 $\color{#9D3DCF}\bf{P6577 【模板】二分图最大权完美匹配}$,可获得 55 分:
```cpp
#include<bits/stdc++.h>
using namespace std;
const int N=505;
long long w[N][N];
long long la[N],lb[N];
bool va[N],vb[N];
long long match[N];
long long n,m,upd[N];
bool dfs(int x){
va[x]=1;
for(int y = 1; y<=n; y++){
if(!vb[y]){
if(la[x]+lb[y]-w[x][y]==0){
vb[y]=1;
if(!match[y]||dfs(match[y])){
match[y]=x;
return true;
}
}else upd[y]=min(upd[y],(la[x]+lb[y]-w[x][y]));
}
}
return false;
}
long long KM(){
memset(match,0,sizeof match);
memset(lb,0,sizeof lb);
for(int i = 1; i<=n; i++){
la[i]=w[i][1];
for(int j = 2; j<=n; j++) la[i]=max(la[i],w[i][j]);
}
for(int i = 1; i<=n; i++){
memset(upd,0x7f,sizeof upd);
while(true){
memset(va,0,sizeof va);
memset(vb,0,sizeof vb);
if(dfs(i)) break;
long long delta=(0x7fffffff);
for(int j = 1; j<=n; j++) if(!vb[j]) delta=min(delta,upd[j]);
for(int j =1;j<=n;j++){
if(va[j]) la[j]-=delta;
if(vb[j]) lb[j]+=delta;
}
}
}
long long ans=0;
for(int i = 1; i<=n; i++) ans+=w[match[i]][i];
return ans;
}
int main(){
memset(w,-127,sizeof w);
cin>>n>>m;
long long u,v,c;
while(m--){
cin>>u>>v>>c;
w[u][v]=c;
}
cout<<KM()<<'\n';
for(int i =1 ;i<=n; i++){
cout<<match[i]<<' ';
}
return 0;
}
```
注意到每次修改顶标后,相等子图只会扩大,原来在相等子图中的边不会消失,这启发我们在每次 dfs 中的很多访问都是多余的(遍历过的交错树没有必要再次遍历)。
实际上,我们只需要从 $A_i + B_j-w_{i,j}$ 最小的边继续向下搜索(即新加入相等子图的边)。
具体实现中,我们可以记录一个数组 $upd_j$ 表示每个右部点 $j$ 对应的最小 $\Delta$,当一个点无法在当前的相等子图中找到匹配时,我们更新顶标,直接从最小边开始下一次 dfs。匹配成功后,由于 dfs 不一定从根节点开始,所以不能使用回溯更新增广路,不妨记录一个 $last_j$ 数组表示每一个右部点 $j$ 在交错树的上一个右部点,沿着 $last_j$ 倒推即可找出增广路。时间复杂度为 $\Theta (n^3)
实测可获得 100 分:
#include<bits/stdc++.h>
using namespace std;
const int N=505;
long long w[N][N];
long long la[N],lb[N];
bool va[N],vb[N];
long long match[N];
long long n,m,upd[N];
long long last[N];
bool dfs(int x,int fa)
{
va[x]=1;
for(int y = 1; y<=n; y++)
{
if(!vb[y])
{
if(la[x]+lb[y]-w[x][y]==0)
{
vb[y]=1;
last[y]=fa;
if(!match[y]||dfs(match[y],y))
{
match[y]=x;
return true;
}
}
else if(upd[y]>la[x]+lb[y]-w[x][y])
{
upd[y]=la[x]+lb[y]-w[x][y];
last[y]=fa;
}
}
}
return false;
}
long long KM()
{
memset(match,0,sizeof match);
memset(lb,0,sizeof lb);
for(int i = 1; i<=n; i++)
{
la[i]=w[i][1];
for(int j = 2; j<=n; j++) la[i]=max(la[i],w[i][j]);
}
for(int i = 1; i<=n; i++)
{
memset(upd,0x7f,sizeof upd);
memset(va,0,sizeof va);
memset(vb,0,sizeof vb);
memset(last,0,sizeof last);
int st=0;
match[0]=i;
while(match[st])
{
if(dfs(match[st],st)) break;
long long delta=(0x7fffffff);
for(int j = 1; j<=n; j++) if(!vb[j] && upd[j]<delta) delta=upd[j],st=j;
for(int j =1; j<=n; j++)
{
if(va[j]) la[j]-=delta;
if(vb[j]) lb[j]+=delta;
else upd[j]-=delta;
}
vb[st]=1;
}
while(st)
{
match[st]=match[last[st]];
st=last[st];
}
}
long long ans=0;
for(int i = 1; i<=n; i++) ans+=w[match[i]][i];
return ans;
}
int main()
{
memset(w,-127,sizeof w);
cin>>n>>m;
long long u,v,c;
while(m--)
{
cin>>u>>v>>c;
w[u][v]=c;
}
cout<<KM()<<'\n';
for(int i =1 ; i<=n; i++)
{
cout<<match[i]<<' ';
}
return 0;
}
值得一提的是,网上会有许多资料显示上文所述的 \Theta(n^3) dfs 实现 KM 算法是用 bfs 实现的,读者可以阅读这篇文章对比一下区别(笔者并不认为有什么区别)。
【谁再催更我不写了】 不写你个der啊,屑 lmw (自己叉自己)……