void dfs1(int u, int p)
{
fa[u] = p;
de[u] = de[p] + 1;
sz[u] = 1;
for (int i = head[u]; i; i = e[i].nxt)
{
int v = e[i].to;
if (v == p) continue;
dfs1(v, u);
sz[u] += sz[v]; // 计算子树大小
if (sz[v] > sz[son[u]])
son[u] = v; // 计算重儿子
}
}
dfs2
void dfs2(int u, int h)
{
top[u] = h;
if (!son[u]) return; // 没儿子
dfs2(son[u], h); // 重儿子的链头跟自己一样
for (int i = head[u]; i; i = e[i].nxt)
{
int v = e[i].to;
if (v == son[u] || v == fa[u]) continue;
dfs2(v, v); // 轻儿子的链头是儿子自己
}
}
LCA
void lca()
{
while (m--)
{
int x, y;
cin >> x >> y;
while (top[x] != top[y]) // 跳到为同一条重链为止
{
if (de[top[x]] < de[top[y]]) swap(x, y); // 把x放到链头较深的重链上
x = fa[top[x]]; // 穿过轻边,去到上一条重链
}
cout << (de[x] < de[y] ? x : y) << endl;
}
}
二叉查找树/平衡树/BST
fhq treap(别问我为啥是这个最先)
treap,即tree+heap,基于二叉查找树与堆的结合体。
每个节点分配两个属性,键值(key)与优先级(pri)。
fhq treap基于两个基本操作:分裂(split)与合并(merge)。
split:
定义为void Split(int u, int v, int <, int &rt) 。
作用,将以u为根的子树按键值v分裂,返回以lt与rt为根的两棵子树。
void Split(int u, int v, int <, int &rt)
{
if (u == 0)
{
lt = rt = 0;
return;
}
if (t[u].key <= v)
{
lt = u;
Split(t[u].rs, v, t[u].rs, rt);
}
else
{
rt = u;
Split(t[u].ls, v, t[u].ls, lt);
}
}
merge:
定义为void Merge(int x, int y) 。
作用,将以x与y为根的子树按优先级合并,返回新树的根。
int Merge(int x, int y)
{
if (x == 0 || y == 0) return x + y;
if (t[x].pri > t[y].pri)
{
t[x].rs = merge(t[x].rs, y);
return x;
}
else
{
t[y].ls = merge(x, t[y].ls);
return y;
}
}
```cpp
#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 5;
//fh[q] tre[a]p
int cnt, root;
struct node
{
int ls, rs, key, pri, sz;
} t[N];
void create(int x, int p)
{
cnt++;
t[cnt].ls = t[cnt].rs = 0;
t[cnt].key = x; t[cnt].pri = p;
t[cnt].sz = 1;
}
void update(int u)
{
t[u].sz = t[t[u].ls].sz + t[t[u].rs].sz + 1;
}
void Split(int u, int v, int <, int &rt)
{
if (u == 0)
{
lt = rt = 0;
return;
}
if (t[u].key <= v)
{
lt = u;
Split(t[u].rs, v, t[u].rs, rt);
}
else
{
rt = u;
Split(t[u].ls, v, lt, t[u].ls);
}
update(u);
}
int Merge(int x, int y)
{
if (x == 0 || y == 0) return x + y;
if (t[x].pri > t[y].pri)
{
t[x].rs = Merge(t[x].rs, y);
update(x);
return x;
}
else
{
t[y].ls = Merge(x, t[y].ls);
update(y);
return y;
}
}
void insert(int x, int p)
{
int l, r, nt;
Split(root, x, l, r);
create(x, p);
nt = Merge(l, cnt);
root = Merge(nt, r);
}
void del(int x)
{
int l, r, nt, f;
Split(root, x, l, r);
Split(l, x - 1, l, nt);
nt = Merge(t[nt].ls, t[nt].rs);
root = Merge(Merge(l, nt), r);
}
void rk(int x)
{
int l, r;
Split(root, x - 1, l, r);
printf("%d\n", t[l].sz + 1);
root = Merge(l, r);
}
int k_th(int u, int k)
{
if (t[t[u].ls].sz + 1 == k) return u;
else if (t[t[u].ls].sz >= k) k_th(t[u].ls, k);
else k_th(t[u].rs, k - t[t[u].ls].sz - 1);
}
void pre_of_x(int x)
{
int l, r;
Split(root, x - 1, l, r);
int u = k_th(l, t[l].sz);
printf("%d\n", t[u].key);
Merge(l, r);
}
void next_of_x(int x)
{
int l, r;
Split(root, x, l, r);
int u = k_th(r, 1);
printf("%d\n", t[u].key);
Merge(l, r);
}
void debug()
{
for (int i = 1; i <= cnt; i++)
printf("%d %d %d %d %d %d\n", i, t[i].ls, t[i].rs, t[i].key, t[i].pri, t[i].sz);
}
int n;
int main()
{
random_device seed;
mt19937 r(seed());
uniform_int_distribution <int> p(1, 2e9);
scanf("%d", &n);
while (n--)
{
int op, x;
scanf("%d%d", &op, &x);
switch (op)
{
case 1: insert(x, p(r)); break;
case 2: del(x); break;
case 3: rk(x); break;
case 4: printf("%d\n", t[k_th(root, x)].key); break;
case 5: pre_of_x(x); break;
case 6: next_of_x(x); break;
}
//debug();
}
return 0;
}
```
#### Splay
Splay 的核心是用旋转维护平衡性。
记左旋为 $zag$ , 右旋 $zig$ 。
单旋 (仅展示 $zig$ )
before:
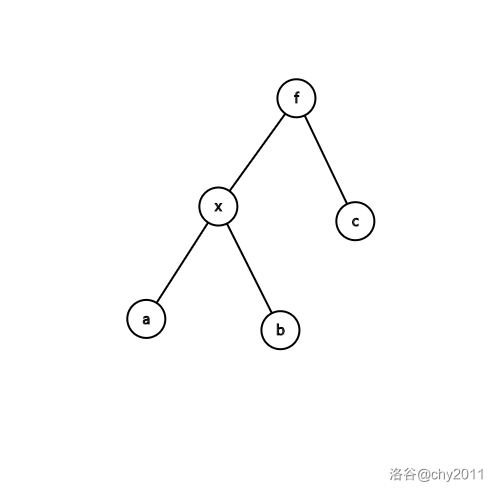
after:
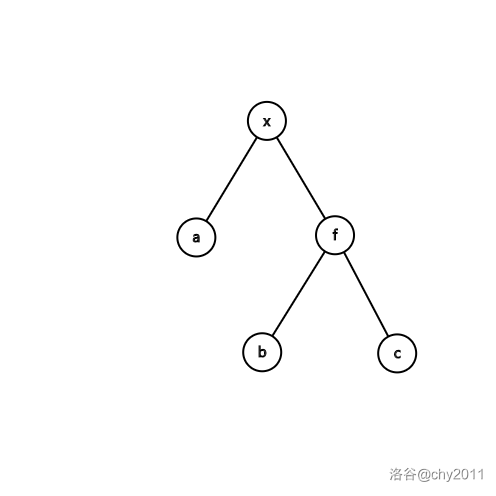
一字旋重点,设要旋的是 $x$ ,父亲是 $f$ ,祖父为 $g$ 。
先旋 $f,g$ , 再旋 $x,f$ 。
之字旋重点,设要旋的是 $x$ ,父亲是 $f$ ,祖父为 $g$ 。
先旋 $x,f$ , 再旋 $x,g$ 。
[$P4008$](https://www.luogu.com.cn/problem/P4008)代码:
```cpp
#include <bits/stdc++.h>
using namespace std;
const int N = 2e6 + 5;
int cnt, root;
struct node
{
int fa, ls, rs, sz;
char key;
} t[N];
void update(int u) {t[u].sz = t[t[u].ls].sz + t[t[u].rs].sz + 1;}
char s[N], op[10];
int build(int l, int r, int fa)
{
if (l > r) return 0;
int mid = (l + r) >> 1;
int now = ++cnt;
t[now].fa = fa;
t[now].key = s[mid];
t[now].ls = build(l, mid - 1, now);
t[now].rs = build(mid + 1, r, now);
update(now);
return now;
}
int get(int u) {return t[t[u].fa].rs == u;}
void rotate(int u)
{
int f = t[u].fa, g = t[f].fa, son = get(u), fson = get(f);
if (son)
{
t[f].rs = t[u].ls;
if (t[f].rs) t[t[f].rs].fa = f;
}
else
{
t[f].ls = t[u].rs;
if (t[f].ls) t[t[f].ls].fa = f;
}
t[f].fa = u;
if (son) t[u].ls = f;
else t[u].rs = f;
t[u].fa = g;
if (g)
{
if (fson) t[g].rs = u;
else t[g].ls = u;
}
update(f); update(u);
}
void splay(int u, int goal)
{
if (!goal) root = u;
while (1)
{
int f = t[u].fa, g = t[f].fa;
if (f == goal) break;
if (g != goal)
{
if (get(u) == get(f)) rotate(f);
else rotate(u);
}
rotate(u);
}
update(u);
}
int k_th(int u, int k)
{
if (t[t[u].ls].sz + 1 == k) return u;
if (t[t[u].ls].sz >= k) return k_th(t[u].ls, k);
return k_th(t[u].rs, k - t[t[u].ls].sz - 1);
}
void insert(int k, int len)
{
int x = k_th(root, k), y = k_th(root, k + 1);
splay(x, 0); splay(y, x);
t[y].ls = build(1, len, y);
update(y); update(x);
}
void del(int l, int r)
{
int x = k_th(root, l), y = k_th(root, r + 1);
splay(x, 0); splay(y, x);
t[y].ls = 0;
update(y); update(x);
}
void prt(int u)
{
if (u == 0) return;
prt(t[u].ls);
putchar(t[u].key);
prt(t[u].rs);
}
int n, cur = 1;
void calc(int len)
{
int x = k_th(root, cur), y = k_th(root, cur + len + 1);
splay(x, 0); splay(y, x);
prt(t[y].ls);
putchar('\n');
}
int main()
{
t[1].sz = t[1].ls = 2;
t[2].sz = t[2].fa = 1;
root = 1; cnt = 2;
scanf("%d", &n);
while (n--)
{
int len;
scanf("%s", op);
switch(op[0])
{
case 'I':
scanf("%d", &len);
for (int i = 1; i <= len; i++)
{
char ch = getchar();
while (ch < 32 || ch > 126) ch = getchar();
s[i] = ch;
}
insert(cur, len);
break;
case 'D':
scanf("%d", &len); del(cur, cur + len); break;
case 'G':
scanf("%d", &len); calc(len); break;
case 'M':
scanf("%d", &len); cur = len + 1; break;
case 'P':
cur--; break;
case 'N':
cur++; break;
}
}
return 0;
}
```