P4967 黑暗打击
LuckiestShawn
·
·
题解
矩阵加速+扩展欧拉定理
题意
题目描述的很清楚了,加油。
思路
我们来观察一下第 3 个图形与第 4 个图形的关系。

$4$ 阶 Hilbert 曲线土壤

**感谢 [if_OF](https://www.luogu.com.cn/user/245033) 的思路和图片。**
$\color{blue}{blue}$ 的部分是可以灌水的区域。
$\color{yellow}{yellow}$ 的部分是新增的用于连接其他 $4$ 个区域同时也被灌了水的区域。
$\color{orange}{orange}$ 的部分是不能灌水的区域。
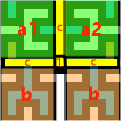
我们可以把 $3$ 阶 Hilbert 曲线土壤分成 上面一半的一半 $a$、下面一半的一半 $b$、中间的新生成的区域 $c$ 这 $3$ 个部分,整个图形的灌水的面积为 $2a+2b+3c+1$。这里黄色部分用三条相等的线段( $c$ )和一个点表示,因为用 $c$ 好递推。
我们同样把 $4$ 阶 Hilbert 曲线土壤用 $a$ $b$ $c$。
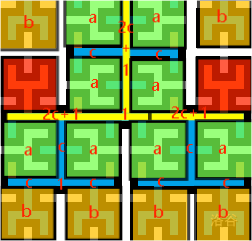
红色部分是无法灌溉的部分。
不难发现,$4$ 阶图形的
$$a_4=2a_3+1b_3+c_3$$
$$b_4=2a_3+2b_3+3c_3+1$$
$$c_4=2c_3+1$$
推广到 $n$ 阶图形
$$a_n=2a_{n-1}+1b_{n-1}+c_{n-1}$$
$$b_n=2a_{n-1}+2b_{n-1}+3c_{n-1}+1$$
$$c_n=2c_{n-1}+1$$
$$s_n=2a_n+2b_n+3c_n+1$$
$s_n$ 为第 $n$ 个图形的面积。
写成矩阵就是:
$$
\begin{bmatrix}
a & b & c & 1 \\
\end{bmatrix}
\times
\begin{bmatrix}
2 & 2 & 0 & 0 \\
1 & 2 & 0 & 0 \\
1 & 3 & 2 & 0 \\
0 & 1 & 1 & 1 \\
\end{bmatrix}^{k}
$$
$a$ $b$ $c$ 初始化为 $2$ 阶 Hilbert 曲线土壤,即 $0$ $1$ $1$,因为从二阶曲线土壤开始,所以 $k$ 初始化为 $n-2$。
矩阵加速做就是了。
但是!!!$n\le 10^{10000}$,这怎看都得炸。如何降幂呢?这里并不能使用 [扩展欧拉定理](https://www.luogu.com.cn/problem/P5091) 降幂,因为扩展欧拉定理并不能直接降矩阵的幂,具体见 [这篇](https://www.luogu.com.cn/discuss/577640) 讨论,但结论是一样的。
思路大概是这样的,具体见代码。
```cpp
#include <iostream>
#include <stdio.h>
#define mod 9223372036854775783ll
#define int __int128
using namespace std;
/* 9223372036854775783 就是质数,所以 phi(...) = ...-1 */
int n,phi = mod-1;
/* 降幂 */
inline int read()
{
char ch;
int in = 0;
bool type = false;
ch = getchar();
while('0'<=ch&&ch<='9')
{
in = ((in<<3)+(in<<1)+(ch-'0'))%phi;
if(in>=phi)
in %= phi,type = true;
ch = getchar();
}
// 不要忘加 phi了
if(type)
in += phi;
return in;
}
/* 按位输出 */
void print(int n)
{
if(n<0){putchar('-');n*=-1;}
if(n>9) print(n/10);
putchar(n % 10 + '0');
return ;
}
struct Trix{
int n,m;
int t[10][10];
}dp,A;
/* 矩阵乘法 */
Trix operator *(Trix a,Trix b)
{
Trix c;
c.n = a.n,c.m = b.m;
for(int i=1;i<=a.n;i++)
for(int l=1;l<=b.m;l++)
c.t[i][l] = 0;
for(int i=1;i<=a.n;i++)
for(int l=1;l<=b.m;l++)
for(int j=1;j<=a.m;j++)
c.t[i][l] = (c.t[i][l]+a.t[i][j]*b.t[j][l]%mod)%mod;
return c;
}
/* 矩阵快速幂 */
Trix fastpow(Trix a,int b)
{
Trix c;
c.n = a.n,c.m = a.m;
for(int i=1;i<=a.n;i++)
{
for(int j=1;j<=a.m;j++)
c.t[i][j] = 0;
c.t[i][i] = 1;
}
while(b>0)
{
if(b&1)
c = c*a;
a = a*a;
b >>= 1;
}
return c;
}
signed main()
{
n = read();
/* 从第二次迭代开始 */
dp.n = 1,dp.m = 4;
dp.t[1][1] = 0;
dp.t[1][2] = 1;
dp.t[1][3] = 1;
dp.t[1][4] = 1;
/* 初始矩阵 */
A.n = A.m = 4;
A.t[1][1] = 2; A.t[1][2] = 2; A.t[1][3] = 0; A.t[1][4] = 0;
A.t[2][1] = 1; A.t[2][2] = 2; A.t[2][3] = 0; A.t[2][4] = 0;
A.t[3][1] = 1; A.t[3][2] = 3; A.t[3][3] = 2; A.t[3][4] = 0;
A.t[4][1] = 0; A.t[4][2] = 1; A.t[4][3] = 1; A.t[4][4] = 1;
dp = dp*fastpow(A,n-2);
print((dp.t[1][1]*2+dp.t[1][2]*2+dp.t[1][3]*3+1)%mod);
return 0;
}
```