后缀自动机学习笔记(干货篇)
command_block
·
2019-06-30 12:02:17
·
个人记录
-1.前面的话
请配合后缀自动机学习笔记(应用篇)食用。
SAM模板的学习原则 : 理解性默写。
-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-
0.概(che)论(dan)
首先您要知道自动机是个什么东西,建议先去学习\bf AC 自动机 。
蒟蒻的理解:有限自动机$=$一个`DAG`,边上有字母,每走过一条边就相当于带上这个字母。
$\color{blue}\text{约定}:$ 从源点**到某个节点的路径**可以形成的所有字符串,称为该节点能够表示的字符串(集合)。
然后,某个自动机所有节点表示的字符串的集合取并,就得到该自动机能表示的字符串集合,这个好理解。
比如说, $\rm Tire$ 就能表示各个字符串的所有**前缀**。
那么, $\rm SAM$ 能表示某个字符串的所有子串,不多不少,正好是所有子串。
此外,为了分析方便,我们的自动机还要满足 : 任意两点的表示集合不交。
首先,我们证明一个$\color{blue}\text{定理}:$ 假如一个字符串能够被 $\rm SAM$ 表示出来,那么其前缀也能被表示出来。
理解 : 自动机都是一个个字符跳的,如果能跳到这个串,那么也一定经过了所有前缀。
所以我们只要构造一个含有所有**后缀**的自动机,其就含有所有子串。这可能就是 $\rm SAM$ 的名字来源吧……
根据上面的定理,不难想到一个很暴力的算法 : 把原串的所有后缀加入 $\rm Trie$ ,那么所有后缀的所有前缀$=$所有子串。
但是,这可能需要 $O(n^2)$ 个节点,复杂度不知道差到哪里去了……
后缀自动机必须得是是十分高效的,最好点数和边数都是 $O(n)$ 。
我们先来讲一些理论。
-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-
------
# 1.endpos
$\color{blue}\text{约定}:$ 我们定义一个**子串**的 $\rm endpos$ ,是它在原串中**结束位置**的**集合**。
**例** : 原串是 $\texttt{ababcb}$ ,那么 ${\rm endpos}(\texttt{ab})=\{2,4\};\ {\rm endpos}(\texttt{b})=\{2,4,6\};\ {\rm endpos}(\texttt{c})=\{5\}$。
下面会简称 $\rm endpos$ 为 $\rm edp$。
我们很快就能想到把所有的子串按照其 $\rm edp$ 分类,按照套路,这应该是有些性质的。
我们把 $\rm edp$ 相同的一堆子串称为一个**类** (子串的集合)。
下面设两个字符串分别为 $s1,s2$ ,且**约定** $|s1|\leq |s2|$。
- $\color{blue}\text{引理(1.1)}:$ $s1$ 是 $s2$ 的后缀 $\Longleftrightarrow$ ${\rm edp}(s2)\subseteq {\rm edp}(s1)
比如上文的 {\rm edp}(\texttt{ab})=\{2,4\};\ {\rm edp}(\texttt{b})=\{2,4,6\} ,其中 \texttt{b} 就是 \texttt{ab} 的后缀。
- $\color{blue}\text{引理(1.2)}:$ $S1,S2$ 的 ${\rm edp}$ 有交 $\large{\Rightarrow}$ ${\rm edp}(s2)\subseteq {\rm edp}(s1)$ , $s1$ 是 $s2$ 的后缀
$\color{blue}\text{证明}:
因为 {\rm edp} 有交,那么在某个 s1 结尾的地方, s2 与它同在,可得 s1 是 s2 的后缀,然后由\color{blue}\text{引理(1.1)} 易证。
那么我们能得到,两个 {\rm edp} 要么没有交,要么互相包含。
(即,如果长度\max=5 ,长度\min=2 ,那么长度 2,3,4,5 都存在)
由$\color{blue}\text{引理(1.2)}$得到,一个类中的字符串之间必有后缀关系,易证其他的串都是 $Smax$ 的后缀。
我们考虑 $Smax$ 长度大于 $Smin$ 的每个后缀 $St$ ,很明显 $Smin$ 是 $St$ 的后缀
由$\color{blue}\text{引理(1.1)}$得到 ${\rm edp}(St)\subseteq {\rm edp}(Smin)$ 且 ${\rm edp}(Smax)\subseteq {\rm edp}(St)$。
又有 ${\rm edp}(Smin)={\rm edp}(Smax)$ 所以 ${\rm edp}(Smin)={\rm edp}(St)={\rm edp}(Smax)$ (夹住了),证毕。
例 : $\texttt{aabaab}$,那么 ${\rm edp}=\{3,6\}$ 的一类中,有 $\texttt{b,ab,aab}$ ,长度是连续的,且其中前者是后者的后缀。
-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-
------
# 2.parent tree
那么我们证明了三个引理之后,会发现一些奇妙的性质。
这三个引理仿佛在暗示一个**树**结构……
考虑某个类,在这个类长度最长的串 $Smax$ 之前添加一个字符,那么这个新串 $Snew$ 一定不属于这个类。
但是 $Smax$ 是 $Snew$ 的后缀,所以有 ${\rm edp}(Snew)\subseteq {\rm edp}(Smin)$ ,也就是说越添字符, $\rm edp$ 集合越小。(字符越多,对匹配的限制就越紧)
我们可以使用子集关系来建立一颗树,就称作$\rm parent$树。
如图, $\texttt{aababa}$ 的$\rm parent$树。
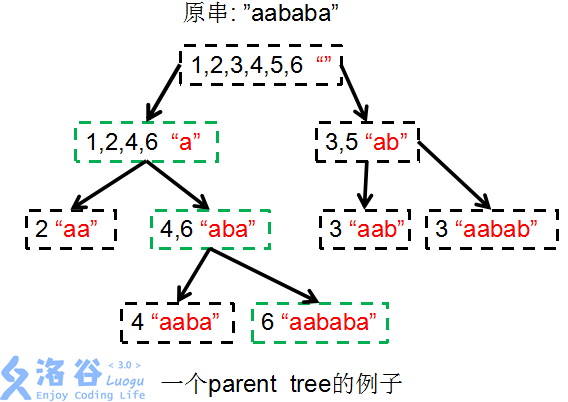
(注意这个图最右边的 `"aabab"` 前面应该写$5$ )
其中,每个节点后面表的是该类中最长的串。
加字符操作,可以理解为分裂 ${\rm edp}$ ,创造儿子的操作。
你可能会发现把 $\{1,2,4,6\}$ 分成 $\{2\}\{4,6\}$ 的时候 $\{1\}$ 不见了,是因为 $\{1\}$ 已经在最前面,不能再加字符了。这个细节不必特别注意,后面不会用到。
那么说了半天,到底这棵树和 $\rm SAM$ 有什么关系呢?
回顾一下 $\rm SAM$ 需要满足的性质 :
1.所有的节点能表示的字符串集合求并$=$该字符串的所有子串
2.任意两个节点的表示集合没有交
3.点和边都是 $O(n)$ 级别的
接下来就要揭晓谜底了 :
这颗树的节点和 $\rm SAM$ 的节点**意义相同**,也就是说这玩意有几个点, $\rm SAM$ 就有几个点,而且**点表示的子串集合也是相同的**。
我们发现这刚好能满足所有的性质,首先,我们是把所有的子串根据 ${\rm edp}$ 分类产生的树,所以这棵树一定含有所有子串。
其次,每个字串的 ${\rm edp}$ 集合是唯一的,不可能被同时分到两个点里面。
$\color{blue}\text{引理(2.1)}$ $\rm parent$树节点数为 $O(n)$。
$\color{blue}\text{证明}:$ 最坏情况下,不考虑消失,那么每加入一个字符,至少把一个类分成两半。
经过 $n-1$ 次分割则能把原来的 $n$ 个都分散,所以最多有 $2n-1$ 个点。
$\color{blue}\text{引理(2.2)}$ 设 $\min(u),\max(u)$ 为$u$这个节点能表示的字符串的最小和最大长度。
若儿子为 $v$ ,父亲为 $u$ ,那么 $\min(v)=\max(u)+1
我们构造这颗树的时候,就指出 : 在最长串前面加字符可以使得 {\rm edp} 分裂。
那么分裂后的 \min(v) 当然 =\max(u)+1 啦。
所以你从\rm parent 树中从上到下拉一条链,你会发现这是个不断在前面加入字符 的过程。
所以,儿子的所有字符串长度都大于父亲的。
我们称上面那些绿色节点(包含后缀的节点,称为终止节点)产生的链为终止链 。
\color{blue}\text{引理(2.3)}$ 基于$\rm parent$树的 $\rm SAM$ 边数不超过 $O(n)
\color{blue}\text{证明}:
非常随便的一个证明……有可能是错的。
首先,从源点出发能到达所有的点,这是毋庸置疑的,我们只留下一颗(有向)生成树,其余的边都删掉。
这样,每个点都可达,也就是说每个点中至少有一个串是能够被表示出来的。
然后我们查看每个终止节点,可能有某些后缀是无法被表示出来的,我们的目标就是将所有后缀恢复。
我们在后缀自动机上恢复一条边,那么肯定多了一条能够到达终止节点的路径。
为什么呢? 非终止节点肯定是有出度的,因为子串可以在后面加上若干字符变成后缀。
又因为这是个DAG,不存在转圈圈的情况,一直走下去,肯定不会停在非终止节点处,所以加一条边就相当于多了至少一条到达终止节点的路径。
也即:恢复了一个后缀 。
那么一共 n 个后缀,所以最多恢复 n 条边就好了。
至此我们发现,如果能够造出基于\rm parent 树的 \rm SAM 的话,就是满足要求的。
-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-=-
3.SAM的构造
先看节点的结构体:
struct SAM_Node
{int t[26],f,len;}这里的 t[26] 表示自动机的转移(类似AC自动机), f 描述了\rm parent 树。
len是每个点能够表示字符串的最大 长度(也就是前面的\max(u) )。
我们采用增量构造法 ,每次从后面加入一个字符。
前面我们说过,只要构造一个含有所有后缀的自动机,其就含有所有子串。
我们把目前新产生的所有后缀都加入自动机 即可。
观察上面的那个图,你会发现一些标绿色的点,这些点被称为终止节点 ,因为他们的 \edp 包含 n ,也就是说这些点里面包含后缀 。
我们新产生的后缀,无非就是在所有旧后缀(包括空)后面再加上一个新字符罢了,那我们的构造工作肯定是从这些终止节点入手。
我们还是对着代码分析吧:
struct SAM_Node
{int t[26],f,len;}
a[...];
int tn,las;
void add(int c)
{
int p=las,np=++tn;las=np;
a[np].len=a[p].len+1;
for (;p&&!a[p].t[c];p=a[p].f)a[p].t[c]=np;
if (!p)a[np].f=1;//case 1
else {
int v=a[p].t[c];
if (a[v].len==a[p].len+1)a[np].f=v;//case 2
else {
int nv=++tn;a[nv]=a[v];
a[nv].len=a[p].len+1;//注意这句话要写在for的前面
for (;p&&a[p].t[c]==v;p=a[p].f)a[p].t[c]=nv;
a[np].f=a[v].f=nv;//case 3
}
}
}
P.S 源点是1首先解释一下 p ,是上一次原串被包含的节点,也就是终止链的末尾。
np 就是我们新建的节点,未来的终止链的末尾。
c 是我们当前要加入的字符。
a[np].len=a[p].len+1;
for(;p&&!a[p].t[c];p=a[p].f)a[p].t[c]=np;前面的一句就是总长++,没别的。
这个for的意思就是顺藤摸瓜,顺着终止链找到原来的所有后缀,然后连一条当前字符的边到np ,这样就能够加入新的后缀。
然后那个终止条件p是为了保证不会跳出源点。
如果最后跳到源点都一切顺利,那么 np 的 f 就指向 1(空集) ,因为没有其他的类包含任何一个新后缀。
!a[p].t[c]的意思则正相反:发现已经有某个点包含了我们要加入的一个后缀,那么长度比其小的后缀就都已经存在了。那么我们不能把这个串加入两次,进入case 2.
v表示包含那个新后缀的节点。
a[v].len==a[p].len+1,也就是说这个点没有比新后缀更长的串 ,那么对其 \rm edp 没有多余的限制 。
于是乎我们就直接把 np 的 f 指向 v ,就满足 {\rm edp}(np)\subseteq {\rm edp}(v) 条件。
不然的话,这个点里面最长的串并不是新后缀。
所以这个点的 \rm edp 在最新意义下并不包含 n ,进入最复杂的case 3。
我们考虑把 v 分裂,一部分包含比新后缀更长的串,一部分包含比新后缀短的串与新后缀本身。
复制一个点叫 nv ,强行让 nv 中最长串是那个新后缀 ,所以有 a[nv].len=a[p].len+1;
然后为了满足没有交这个条件,我们要把新后缀及其后缀从原来的 v 中剔除出去。
如何操作呢,先全部复制 v 到 nv ,
for(;p&&a[p].t[c]==v;p=a[p].f)a[p].t[c]=nv;
然后我们在刚才停下的终止链(包含的都是旧后缀)上继续跳,然后把本来属于 v 的对应入边都夺过来给 nv ,那么一定能从 v 中剔除新后缀(且满足了长度连续的性质)。
现在 nv 的 \rm edp 包含原来的 v (因为更短,限制更小,集合更大),也包含 n 。
所以我们需要令 a[v].f=a[np].f=nv;
那么,一个 \rm SAM 就构造完毕了,完结撒花!
仅仅有一个能够表示字符串所有子串的“黑盒” \rm SAM 是远远不够的,我们将在应用中详细介绍其性质。