CF1081H 【Palindromic Magic】结论的证明
Wen_kr
·
2020-06-18 21:29:20
·
题解
关于证明为什么会移动到这里:
大部分翻译自 CF 题解。
一些定义
没有特殊声明的情况下,我们约定 s 为一个字符串。
约定 s^R 为 s 的反串。
约定 s[i,j] 为由 s 的第 i 到第 j 个字符构成的子串,约定 s[i] 表示 s 的第 i 个字符。
约定 |s| 为字符串 s 中的字符个数。
我们称 t 为 s 的一个 border ,当且仅当 s[1,t]=s[|s|-t+1,|s|] 。
特别地,我们令 border(s) 为 s 最长的 border,如 border('aba')='a' , border('ab')='' (空串)。
不难发现,若 s 是一个回文串,则若 s 存在一个长度为 x 的回文前/后缀,则 x 是它的 border;若 x 是 s 的 border,则 s 也存在一个长度为 x 的回文前/后缀。
证明 :根据 border 的性质,有 \forall i\in[1,x],s[i]=s[t-x+i] ,根据回文串的性质,有 s[i]=s[t-i+1] ,则 s[t-x+i]=s[t-i+1] ,可以发现 s 存在一个长度为 x 的后缀回文串。由存在长度为 x 的后缀回文串推导出存在 border x 类似。
如是,我们可以推出 border(s) 是 s 的最长回文前(后)缀。
我们称 t 为 s 的一个周期 ,当且仅当 \forall i \in [1,|s|-t], s[i]=s[i+t] ,特别地,若 t\mid|s| ,我们称 t 为 s 的一个完全周期 。显然,|s| 一定是 s 的周期。
不难发现,若 t 是 s 的一个周期,则 |s|-t 将会是 s 的一个 border。可以用下图的方式来理解:
由于 t 是 s 的一个周期,所以蓝色和蓝色相等,黄色和黄色相等,粉色和粉色相等。
最后的长度可能不满 t 的粉色部分一定是上一个黄色部分的前缀,所以当 t 是一个周期,则 |s|-t 就会是 s 的一个 border。反之若 |s|-t 是 s 的一个 border,我们可以用类似的方法说明 t 将会是 s 的一个周期。
我们称 s 是一个循环串 ,当且仅当 s 存在一个不等于 |s| 的完全周期 。
记 s^a 表示 s 串重复 a 次后形成的串。
引理 1
若 p,q 均为 s 的周期,且 p+q\leq |s| ,则 gcd(p,q) 也是 s 的一个周期。
证明
令 p<q,d=q-p 。
①
由于 $p+q\leq|s|$,
有 $i-p\geq 1$;$i-p+q=i+d\leq s$,
故 $s[i]=s[i-p]=s[i-p+q]=s[i+d]$;
②
$\forall i\in [1,|s|-q]$,
由于 $p+q\leq |s|,p<q$,
有 $i+q\leq|s|$;$i+q-p> 1$,
故 $s[i]=s[i+q]=s[i+q-p]=s[i+d]$;
③
回忆关于周期串的定义,我们已经证明了 $\forall i\in [1,|s|-d]$,$s[i]=s[i+d]$,不难得出 $d$ 是 $s$ 的一个周期。
由辗转相除法,我们可以反复执行这个操作,最终我们会得到 $gcd(p,q)$ 是 $s$ 的一个周期。
------
### 引理 2
令 $S$ 为 $s$ 的所有 $\leq |s|/2$ 的周期。
若 $S$ 非空,我们可以断言 $\forall u\in S,\min S \mid u$。
$\min S$ 为 $S$ 中的最小元素。
### 证明
令 $v=\min S$,
由于 $\forall u\in S,u\leq |s|/2$,所以 $u+v\leq |s|$,
由引理 $1$ 有 $gcd(v,u)$ 是 $S$ 的周期,
又因为 $v=\min S$,有 $gcd(v,u)\geq v$,因此 $gcd(v,u)=v$,因此 $v\mid u$。
------
令 $S=pq$,$p,q$ 是两个非空回文串,我们称 $(p,q)$ 是一组 $S$ 的**回文拆分**。
若 $S=pq$,$p,q$ 是两个回文串且 $q$ 非空,则我们称 $(p,q)$ 是一组 $S$ 的**非严格回文拆分**。
------
### 引理 3
若 $S=x_1x_2=y_1y_2=z_1z_2$,$|x_1|<|y_1|<|z_1|$,$x_2,y_1,y_2,z_1$ 是非空回文串,则 $x_1,z_2$ 也会是回文串。
### 证明
令 $z_1=y_1v$。
显然 $v^R$ 是 $y_2$ 的一个后缀,由于 $|x_2|>|y_2|$,因此 $v^R$ 也是 $x_2$ 的一个后缀。
由于 $x_2$ 是一个回文串,因此 $v$ 是 $x_2$ 的前缀,所以 $x_1v$ 是 $z_1$ 的一个前缀。
又因为 $y_1$ 是 $z_1$ 的回文前缀,所以 $|v|$ 是 $z_1$ 的一个周期。又因为 $x_1v$ 是 $z_1$ 的一个前缀,因此 $|v|$ 也是 $x_1v$ 的周期。
$x_1v$ 的周期为 $|v|$,因此 $x_1$ 一定能被被拆分成 $v$ 的某个后缀和若干个 $v$,于是存在整数 $t$(你可以直接认为 $t$ 是正无穷),使得 $x_1$ 是 $v^t$ 的一个后缀。
因为 $|v|$ 是 $z_1$ 的周期,$v^R$ 是 $z_1$ 的一个前缀,所以当 $t$ 足够大时,满足 $z_1$ 是 $(v^R)^t$ 的一个前缀。
对于一个足够大的整数 $t$,因为 $x_1$ 是 $z_1$ 的前缀,$z_1$ 是 $(v^R)^t$ 的前缀,所以 $x_1$ 是 $(v^R)^t$ 的前缀,于是 $x_1^R$ 将是 $v^t$ 的一个后缀。因此 $x_1$ 和 $x_1^R$ 都是 $v_t$ 的一个后缀,因此 $x_1$ 是回文串。
用类似的方法,我们可以说明 $z_2$ 也是一个回文串。
------
### 引理 4
若串 $S$ 存在回文拆分(可以非严格),令 $a$ 表示 $S$ 的最长回文前缀,$S=ax$,$b$ 表示 $S$ 的最长回文后缀,$S=yb$,则 $x,y$ 中必然存在至少一个回文串。
### 证明
考虑反证。
若 $x,y$ 均非回文串,令 $pq$ 为 $S$ 的一个回文拆分(可以非严格),显然有 $|q|<|b|$ 即 $|y|<|p|$, $|p|<|a|$(不能取等,因为若取等则 $x,y$ 至少存在一个为回文串)。
则 $S=yb=pq=ax$,由引理 3,可以推出 $x,y$ 均为回文串,矛盾。
------
### 引理 5
若 $S=p_1q_1=p_2q_2$,$(p_1,q_1)$ 与 $(p_2,q_2)$ 是两个 $S$ 的非严格回文拆分且 $|p_1|<|p_2|$,则 $S$ 是一个循环串。
### 证明
可以证明 $gcd(|p_2|-|p_1|,|S|)$ 是 $S$ 的一个周期。
令 $|S|=n$,$|p_2|-|p_1|=t$。
因为 $p_1$ 是 $p_2$ 的一个回文前缀,所以 $p_2$ 有周期 $t$,同理 $q_1$ 也有周期 $t$。
$p_2$ 和 $q_1$ 在 $S$ 上重复覆盖了长度为 $t$ 的部分,且 $p_2$ 和 $q_1$ 加起来完全覆盖了 $S$,因此 $S$ 也有周期 $t$。
$\forall x \in [1,t]$,有 $S_x=S_{|p_2|-x+1}=S_{n+|p_1|-|p_2|+x}=S_{n-t+x}$ (前两个等号是因为 $q_1,p_2$ 为回文串。其中第二个等号的推导过程为:将 $|p_2|-x+1$ 在 $q_1$ 上翻转,翻转后的下标为 $n-(|p_2|-x+1-|p_1|-1)+1$,即为 $n-|p_2|+|p_1|+x$。
由周期的定义,有 $n-t$ 是 $S$ 的一个周期。由于 $t+n-t\leq n$,由引理 $1$,有 $gcd(t,n-t)=gcd(t,n)$ 是 $S$ 的一个周期。由于 $gcd(t,n)\mid n$,$S$ 是一个循环串。
------
### 引理 6
令 $S=p_1q_1=p_2q_2=\cdots=p_tq_t$,且 $\{(p_1,q_1),\cdots,(p_t,q_t)\}$ 是所有 $S$ 的非严格回文拆分,令 $h$ 表示 $S$ 的最小完全周期。则,若 $t\neq 0$,则 $t=|S|/h$。
### 证明
由引理 5,显然有若 $t\neq 0$ 且 $h=|S|$, $t=1$。
于是下面我们按照 $t\geq 2$ 来讨论。
令 $\alpha = S[1,h]$,显然有 $\alpha$ 不是一个循环串,否则 $S$ 就会拥有一个更小的完全周期,因此 $\alpha$ 最多拥有一个非严格回文拆分。
令 $pq$ 为任意一组 $S$ 的非严格回文拆分,有 $\max\{|p|,|q|\}\geq h$。我们默认 $|p|\geq h$($|q|\geq h$ 类似),有:
$\alpha[1,(|p|-1)\bmod h + 1]=p^R[1,(|p|-1)\bmod h+1]
同理,可以类似地利用 $q$ 得到 $\alpha[(|p|-1)\bmod h+2,h]$ 是一个回文串。(下图可以帮助你理解)
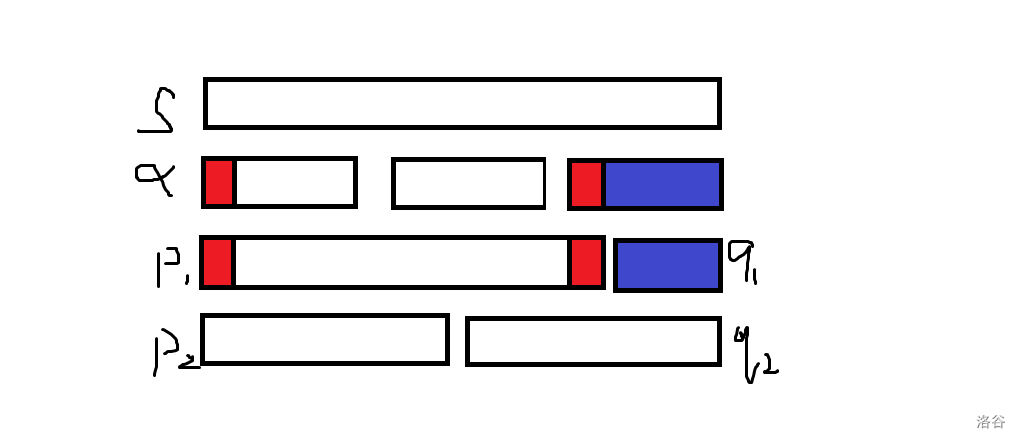
(图上只画出了 $p_1$ 和 $q_1$ 部分,$p_2$ 和 $q_2$ 类似)
于是 $\alpha$ 拥有一个非严格回文拆分,由引理 5 我们还知道 $\alpha$ 只拥有一个非严格回文拆分。令这个回文拆分为 $\alpha[1,g-1],\alpha[g,h]$。因此,每个 $|p_i|$ 都必须满足 $|p_i|\equiv g-1 \pmod h$,于是合法的 $|p_i|$ 只有 $|s|/h$ 种,并且可以说明的是,这 $|s|/h$ 种 $|p_i|$ 都是合法的(可以画画图得知)。
------
### 引理 7
令 $S=p_1q_1=p_2q_2=\cdots=p_tq_t$,且 $\{(p_1,q_1),\cdots,(p_t,q_t)\}$ 是所有 $S$ 的非严格回文拆分($|p_i|<|p_{i+1}|$)。则 $\forall i\in[1,t-1]$,$p_i=border(p_{i+1})$ 和 $q_{i+1}=border(q_i)$ 至少有一项成立。
### 证明
在证明引理之前,我们先来介绍一种求出所有非严格回文拆分的方法。
令 $S$ 的最长的,非 $S$ 的回文前缀为 $a$,令 $S=ax$;令 $S$ 的最长的,**不一定非** $S$ 的回文后缀为 $b$,令 $S=yb$。
若 $x=b$,显然 $S=ab$ 是唯一一种拆分方法。因为若缩短 $a$,不能找到更长的回文后缀;缩短 $b$,不能找到更长的回文前缀。于是我们在下面基于 $x\neq b$ 讨论。
由引理 4,若 $S$ 存在非严格回文拆分,则 $x,y$ 至少有一个是回文串。
因此,若 $x,y$ 皆非回文串,则 $S$ 不存在非严格回文拆分;
若 $x,y$ 只有一个为回文串,则 $S$ 只存在唯一一种非严格回文拆分(考虑若存在另一种非严格回文拆分 $(p,q)$,且 $|p|<|a|,|q|<b$ 即 $|p|>|y|$,由于 $b,a$ 都是回文串可以推出 $x,y$ 都是回文串,矛盾);
否则,$x,y$ 皆为回文串,可以说明 $a$ 非空,因此我们可以找到 $S$ 第二长的,非自身的回文前缀 $c$;令 $S=cz$,若 $z$ 不是回文串或者 $c=y$,则 $S=ax=yb$ 是唯二合法的拆分(若 $c=y$,显然有 $S$ 只有这两种拆分,否则,考虑反证,假设存在另一个拆分 $(p,q)$ 使得 $|p|<|c|$ 且 $|p|>|y|$,可以推出 $z$ 是回文串,矛盾)(令这种情况为情况①);否则,$z$ 是回文串,我们可以找出所有长度介于 $|z|$ 和 $|b|$ 之间的回文后缀,它们对应的前缀也一定是回文串(令这组回文后缀为 $pq$,有 $|p|<|c|<|a|$,有 $c,z,q,a$ 皆为回文串,由引理 3 能得到 $|p|$ 也是回文串,如是我们求出了 $S$ 的所有非严格回文拆分(由于回文后缀的长度不会长于 $|b|$,回文前缀的长度不会长于 $|a|$,因此这样求出的回文拆分是不漏的)。
不难发现,除去情况①,我们都满足 $q_{i+1}=border(q_i)$ 或 $p_i=border(p_{i+1})$(对于 $(c,z)$ 与 $(a,x)$ 这组满足 $p_i=border(p_{i+1})$,其余的满足 $q_{i+1}=border(q_i)$)。
现在我们来证明情况①也满足命题条件。考虑反证法。
假设情况①不正确,即 $border(a)\neq y$ 且 $border(b)\neq x$,$S=ax=yb$,令 $p=border(a),s=border(b)$,$S=ax=pq=rs=yb$,此时 $|a|>|p|>|y|,|a|>|r|>|y|$,且 $p,s$ 是回文串。
由引理 6,我们知道 $S$ 只有两种非严格回文拆分,因此 $S$ 是一个循环串,且 $S=\alpha^2,h=\frac{|S|}{2}$。除此之外,由引理 6 我们还知道 $|a|>|\alpha|$,$|b|>|\alpha|
若 |p|\geq|\alpha| ,有 q=\alpha[|p|\bmod h+1,h] ,由于 p 是回文串,可以推导出 q 也是回文串,矛盾。(如下图,蓝色部分为回文串)
如是,我们有 |p|<|\alpha| ,类似地可以推出 |s|<|\alpha| ,令 \alpha=pq'=r's ,由引理 6 \alpha 有唯一的非严格回文拆分,令这个拆分为 \alpha=\beta\theta 。由于 |\beta|\leq|\alpha| ,且 \beta 是 a 的一个合法 border(见上图),因此此时有 |p|>|\beta| ;同理,此时一定有 |b|>|\theta| ,故 |s|>|\theta| 即 |r'|<|\beta| ,由引理 3,此时 S=r's=\beta\theta=pq' ,可以推出 r' 和 q' 为回文串进而推出 r,q 为回文串,矛盾。
自此,引理准备完毕,我们可以开始说题目了。
为了避免你忘记题目在说什么,这里我们复述一遍题意:给定两个字符串 A,B ,你需要从 A,B 中取出两个非空回文串拼接起来,问这样能拼出多少不同的字符串。两个字符串是不同的当且仅当长度不同或某个位置上字符不同。
考虑怎么统计题上要求的字符串。
不考虑去重,我们可以计数 A 中本质不同的回文串个数和 B 中本质不同的回文串个数,然后将它们两个乘起来。这显然会计重。
考虑引理 7,假设 S=xy ,如果用 border(x) 代替 x 后能得到一种凑出 S 的方法,或者用 border(y) 代替 y 后能得出一种凑出 S 的方法,显然此时 S 就被重复统计了。
现在问题变成了:对于一个 A 中的回文串 x ,我们想要知道有多少个 S 既能从 x 得到又能从 border(x) 得到,然后将答案减去那么多。找到 x 和 border(x) 分别是啥是简单的,只需要一棵回文树即可。
令 x=border(x)w ,我们要数的就是在 B 中有多少个 T ,使得 T=wS ,且 S 和 T 都是 B 中的回文串。因为 |w| 是 x 最短的周期,因此 w 不是一个循环串。
若 |w|>|S| ,则 w 一定可以写成 S+U ,U 是某个回文串(因为要满足 wS 是回文串)。
因为 w 不是一个循环串,由引理 5,w 只有至多一种非严格回文拆分。在引理 7 的证明里我们说明了这个非严格回文拆分一定包含 w 的最长回文前缀/后缀,我们只需要验证这个即可,然后使用哈希验证 S 和 wS 是否在 B 中存在即可。
若 |w|\leq|S| ,若 S 不是 T 的最长回文后缀,记最长回文后缀为 P ,有 |T|-|P| 是一个 T 的周期,还有 |w| 也是一个 T 的周期,由引理 2,有 (|T|-|P|)\mid |w| ,得出 w 是循环串,矛盾。
因此,我们只需要对回文树上所有 S=border(T) ,且 (|T|-|S|)\times 2\leq |T| 的位置判断一遍即可,也可以使用哈希实现。
关于如何找 A 某个子串的最长回文前缀/后缀,你可以在回文树上倍增直到合法。
同理,我们还需要在 B 中数一遍 y 。
注意到这样会额外减掉既能被 border(x) 统计到的,又能被 border(y) 统计到的,因此我们需要在最后额外加回来这种情况。
考虑若此时 w 既是左边那个大串的 border ,又是右边那个串的 border ,且红串属于 A ,蓝串属于 B ,这种情况就会被减去两次,于是只需要加上公共 w 对数即可。