神经元网络的粗略入门
David_H_
·
2020-03-01 21:24:22
·
个人记录
本文是基于@3B1B的视频写的(理解)
具体视频在av15532370,av16144388和av16577449。
\mathop{\text{神经元网络}}\limits_{\texttt{Neuron Network}} 全篇需要微积分与线性代数基础!!!
本篇中,上角标(i) 为第i 个样本。
Pt. 1 \mathop{\text{结构}}\limits_{\texttt{Structure}}
一、\mathop{\text{神经元}}\limits_{\texttt{Neuron}}
在现在,我提到神经元的时候,我是指一个装有数字的容器。如果我们把其所代表的数据设为x的话,那么我们尤指当x\in[0,1] 的数字(所以接下来都是这样的),仅此而已。
二、正题
比如说,我举个栗子。我们面前有一个写着9的28\times28 的矩阵,即总共有784个神经元。(如下图所示)
然后,我们对于每一个像素,都当做一个神经元,代表着一个数,越靠近1越白,反之,越靠近0越黑;即1表示纯白像素,0表示纯黑像素。
我们把里面储存的值,称为\mathop{\text{激活值}}\limits_{\texttt{Activation}} 。
这784个神经元组成了这个神经元网络的第1层。
在第一层(即\mathop{\text{输入层}}\limits_{\texttt{Input Layer}} )和最后一层(即\mathop{\text{输出层}}\limits_{\texttt{Output Layer}} )之间,有很多层(不如暂时当做一个暗箱,然后各个神经元在里面做交易),这些层,我们称为\mathop{\text{隐含层}}\limits_{\texttt{Hidden Layers}} 。
不如说我们把中间的层数设为2层,然后每层有16个(瞎选)。
在他运作的时候,上一层的激活值决定了下一层的激活值。换而言之,就是说一层的激活值是通过某种神奇的计算,得到下一层的激活值的。从某种程度上来说,其目的是为了模仿生物中的神经元组成的网络。(例如,深度残差收缩网络达到了1000+层 )。(怎么感觉有点像树形DP)
而输出层最亮的(或者说激活值最高的)那个神经元就是神经网络的“选择”,即它认为输入图像里写着这个数字。
可是,我们希望中间层能够做什么呢?比如说我们希望分辨“9”,我们要怎么分辨呢?
我们可以把9拆分成更小的部件:“o”和“|”,接着可以把这些拆成更小的部件。(如“o”变成更小的边)这是我们的一个希望。
现在,问题来了,你要怎么联系上一层到下一层?我们不如举个例子吧,从输入层到第一个隐藏层的一个神经元的识别区域,我们可以来一个权重函数w_i ,使得前面的每一个激活值a_i 需要乘上这个权重,写出来就是\sum\limits_{i=1}^{n}w_ia_i ,即算出他们的加权和。
对于每一个识别区域,我们把该区域的权重w 设为正的,其余的均设为0,这样就仅仅会累加我们所关注区域的像素值,或激活值了。如果你想真正的知道哪里是否有一条边,那么只需要给周围一圈像素赋予负权重就行了。
算出来的可以在任意大小,可我们希望的值在[0,1] 这个区间内,我们就很自然的想到是否需要一个函数了。可恰恰有函数是这样的——\texttt{sigmoid} 函数,即
\sigma(x)=\dfrac{1}{1+\mathrm{e}^{-x}}
(或\mathop{\text{逻辑斯蒂曲线}}\limits_{\texttt{Losgistic Curve}} )画出来就是这样的:
所以我们所需要的就是\sigma\left(\sum\limits_{i=1}^{n}w_ia_i\right) ,即他的打分。
如果你想要给他一些\mathop{\text{偏置}}\limits_{\texttt{Bias}} ,也就是说,你想让他超过某些数值才有意义,我们就可以记作\sigma\left(\sum\limits_{i=1}^{n}w_ia_i-\underbrace{b}_{\text{偏置}}\right)
对于每一个神经元,都带有一个\mathop{\text{权重}}\limits_{\texttt{Weight}} ,即总13002 个数值(每个数值你都要调,这个过程就叫做“\mathop{\text{学习}}\limits_{\texttt{Learning}} ”)。
最后提一嘴,如果我们要写的话,比如说输入层的n 个数为a_n^{(i)} ,权重表示为w_{i,j} ,其中i,j 分别表示第j 个(值a_n^{(i)} 中的i )和第i 个(从上往下数的该层神经元的编号),则我们可以写成:
\sigma\left(
\begin{bmatrix}
w_{0,0} & w_{0,1} & \cdots & w_{0,n} \\
w_{1,0} & w_{1,1} & \cdots & w_{1,n} \\
\vdots & \vdots & \ddots & \vdots\\
w_{n,0} & w_{n,1} & \cdots & w_{n,n}
\end{bmatrix}
\begin{bmatrix}
a_0^{(0)}\\
a_1^{(0)}\\
\vdots\\
a_n^{(0)}\\
\end{bmatrix}
+
\begin{bmatrix}
b_0\\
b_1\\
\vdots\\
b_n\\
\end{bmatrix}
\right)
注意,这里的包起来是指对矩阵里的每一项都去\sigma(x) 函数,即:
b_0\\
b_1\\
\vdots\\
b_n\\
\end{bmatrix}\right)=
\begin{bmatrix}
\sigma(b_0)\\
\sigma(b_1)\\
\vdots\\
\sigma(b_n)\\
\end{bmatrix}
抱歉,这次我真的得用\mathtt{Python} 了……
额,最后说一下,现在的Sigmoid已经过时了,我们一般用的是
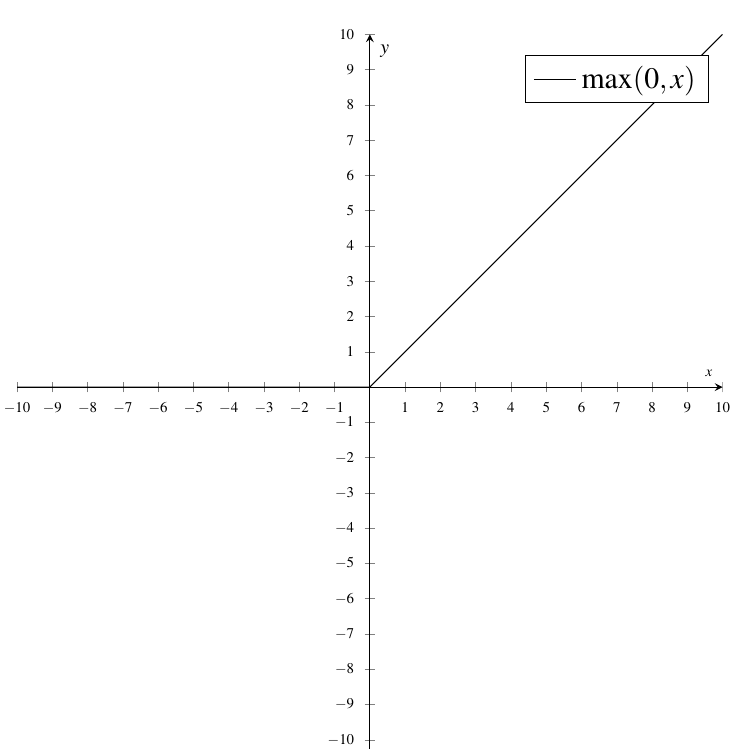
即,我们现在一般用:
$$
\mathrm{ReLU}\left(
\begin{bmatrix}
w_{0,0} & w_{0,1} & \cdots & w_{0,n} \\
w_{1,0} & w_{1,1} & \cdots & w_{1,n} \\
\vdots & \vdots & \ddots & \vdots\\
w_{n,0} & w_{n,1} & \cdots & w_{n,n}
\end{bmatrix}
\begin{bmatrix}
a_0^{(0)}\\
a_1^{(0)}\\
\vdots\\
a_n^{(0)}\\
\end{bmatrix}
+
\begin{bmatrix}
b_0\\
b_1\\
\vdots\\
b_n\\
\end{bmatrix}
\right)
$$
## Pt. 2 $\mathop{\text{梯度下降法}}\limits_{\texttt{Gradient Descent}}
这里,我们需要对它进行梯度下降法的过程进行一个简化,如果你真正的理解了以后,那不过就是几道微积分问题了(听起来更糟)。
对于这里的“机器学习”,就相当于梯度下降法(如果你听懂了的话),这其实就是在找一个函数的最小值。
一、具体过程
在一开始,我们先随机地初始化所有的权重w_i 和偏置b ,也就是说,它不一定会识别出来测试样例。
比如说输入一个测试用的“3”,然后输出层看起来一团糟,这时候就要定义一个\mathop{\text{代价函数(损失函数)}}\limits_{\texttt{Cost Function(Loss Function)}} 来告诉电脑:“你个坏电脑(\text{No! Bad computer(Network)!} ),正确输出的激活值应该是0,只有这个是1!但你给我的都是乐色!”
那么,这个代价函数要怎么定义呢?你需要将每个它所输出的乐色激活值与你想要的值之间的差的平方加起来,这个,我们就称之为训练单个样本的“\mathop{\text{代价(损失)}}\limits_{\texttt{Cost(Loss)}} ”。我们注意到,当网络能够对图像正确的进行分类时,该平方和就较小。
我们可以发现,这些代价函数都有一个特点:在图像能够对图像进行正确分类时,这个代价函数所返回的值就比较小;反之,当这个网络找不到北的时候,这个返回值就会较大。
这时,你就会把手头上成千上百的输入输进去,返回的所有代价的平均值(称为\mathop{\text{经验风险}}\limits_{\texttt{Empircal Risk}} )来评价这个网络有多糟糕,电脑应该有多“内疚”。
注意,这个函数的输入是这么多(13002个)个数字,输出单个数值来判断这些权重和偏置值有多么的差劲,取决于成千上万的输入数据。
我们来简化问题吧!与其说考虑一个代价函数:C(\underbrace{w_1,w_2,\cdots,w_{13002}}_{\text{权重和偏置}}) (13000个变量),我们不如先考虑一个简单的一元函数C(\underbrace{w}_{\text{单一的输入变量}}) ,只有一个输入变量并且只输出一个数字。
那你应该怎么找使这个一元的输入值w_0 ,使得输出值最小化呢?如果你微积分足够棒,你可以直接算出来:\dfrac{\mathrm{d}C}{\mathrm{d}w}(w)=0 时。但是,当函数很复杂的时候(如下图),就不一定能够写出来。
自然,如果回归到本来的问题的话,13002元的代价函数就自然更不可能做到了。
一个相较于更加灵活的方法是,先挑一个输入值,再考虑,是向左还是向右,这样函数值才会变小。即,分析出该点的斜率\gamma ,若\gamma\in(0,+\infty) 时,向左走;当\gamma\in(-\infty,0) 时,向右走;当\gamma=0 时,不动(说明已经到最低点了)。
通过上面的过程,你可以分析出函数的局部最小值。同时,我们让每一步的步数与斜率成比例,这样在最小值附近,每步会越来越小。
那么,我们来复杂化一下问题吧,想想一个输入2个,输出1个的2元函数C(x,y) 。你可以把这个想象成输出在xOy平面直角坐标系上,输入则在上方的曲面上。那么,对于每一步,你需要扪心自问,在输入空间内向哪个方向走,这样输出结果下降的最快。换句话来说,就是怎么下山最快(用球滚下山来类比)。
熟悉多元微积分的人一定知道,函数的梯度\nabla C(x,y) 指出了函数的最陡增长方向。也就是说,按着梯度的方向走,函数值就增长的越快。自然地,我们可以想到,沿着它的负方向走,函数值自然下降的最快了。
同时,这个梯度向量的长度就代表了这个最陡的斜坡有多陡。
(计算方法:\nabla C(x,y)=\begin{bmatrix}
\dfrac{\partial C}{\partial x}\\
\dfrac{\partial C}{\partial y}\\
\end{bmatrix}=\begin{bmatrix}
zx\\zy
\end{bmatrix} )
所以,你应该知道应该怎么算了,即先计算坡度\nabla C ,然后再-\nabla C 的方向走一小步,重复以上操作即可。
处理带13002个输入的函数也是一样,你可以把所有的权重和偏置放进一个向量内。例如:\vec{\mathbf{W}}=\begin{bmatrix}2.25\\-1.57\\1.98\\\vdots\\-1.16\\3.82\\1.21\end{bmatrix}
那么,代价函数也不过是个向量:-\nabla C(\vec{\mathbf{W}})=\begin{bmatrix}0.18\\0.45\\-0.51\\\vdots\\0.40\\-0.32\\0.82\end{bmatrix} 。
负梯度也不过是想支出具体如何改变每一项参数,才可以让代价函数下降的最快。所以新的\vec{\mathbf{W}}=\vec{\mathbf{W}}_{(old)}+(-\nabla C(\vec{\mathbf{W}}))
Pt. 2.5 更具体的讲一讲代价函数
参考资料:https://www.cnblogs.com/Belter/p/6653773.html
假设有训练样本(x, y) ,模型为h ,参数为θ 。h(θ) = θ^Tx (θ^T 表示θ 的\mathop{\text{转置}}\limits_{\texttt{Transposition}} )。
(1)概况来讲,任何能够衡量模型预测出来的值h(θ) 与真实值y 之间的差异的函数都可以叫做代价函数C(θ) ,如果有多个样本,则可以将所有代价函数的取值求均值,记做J(θ) 。因此很容易就可以得出以下关于代价函数的性质:
(2)当我们确定了模型h ,后面做的所有事情就是训练模型的参数θ 。那么什么时候模型的训练才能结束呢?这时候也涉及到代价函数,由于代价函数是用来衡量模型好坏的,我们的目标当然是得到最好的模型(也就是最符合训练样本(x, y) 的模型)。因此训练参数的过程就是不断改变θ ,从而得到更小的J(θ) 的过程。理想情况下,当我们取到代价函数J的最小值时,就得到了最优的参数θ ,记为:
\min_{\theta}J(\theta)
例如,J(θ) = 0 ,表示我们的模型完美的拟合了观察的数据,没有任何误差。
(3)在优化参数θ的过程中,最常用的方法是梯度下降,这里的梯度就是代价函数J(θ) 对θ_1, θ_2, ..., θ_n 的\mathop{\text{偏导数}}\limits_{\texttt{Partial Derivative}} 。由于需要求偏导,我们可以得到另一个关于代价函数的性质:
选择代价函数时,最好挑选对参数θ\mathop{\text{可微}}\limits_{\texttt{Differentiability}} 的函数(\mathop{\text{全微分}}\limits_{\texttt{Total Differential}} 存在,偏导数一定存在)
常用的代价函数有3种,但有一种我们不理解,故不在此赘述,分别是:(参考资料)
①均方误差:(即文中提到的,一般在线性回归中最常用)
J(\theta_0,\theta_1)=\dfrac{1}{2m}\sum_{i=1}^{m}(\hat{y}^{(i)}-y^{(i)})^2=\dfrac{1}{2m}\sum_{i=1}^{m}(h_{\theta}(x^{(i)})-y^(i))^2
其中,m 为训练样本的个数;\hat{y}^{(i)}=h_θ(x) 为用参数θ 和x 预测出来的y 值(在这里指激活值);y 为原训练样本中的y 值(在这里指激活值),也就是标准答案;上角标(i) 为第i 个样本。
②交叉\mathop{\text{熵}}\limits^{\mathrm{shāng}} ,在《神经网络与深度学习》一书中,对交叉熵的解释就是:
交叉熵是对「出乎意料」(译者注:原文使用 suprise )的度量。神经元的目标是去计算函数y , 且y=y(x) 。但是我们让它取而代之计算函数a , 且a=a(x) 。假设我们把a 当作y 等于1 的概率,(1-a) 是y 等于0 的概率。那么,交叉熵衡量的是我们在知道y的真实值时的平均「出乎意料」程度。当输出是我们期望的值,我们的「出乎意料」程度比较低;当输出不是我们期望的,我们的「出乎意料」程度就比较高。
J(\theta)=-\dfrac{1}{m}\left[\sum_{i=1}^m(y^{(i)}\log h_{\theta}(x^{(i)})+(1-y^{(i)})\log(1-h_{\theta}(x^{(i)}))\right]
说明同上。
\mathop{\text{回顾}}\limits_{\texttt{Recap}}
\mathop{\text{代价函数(损失函数)}}\limits_{\texttt{Cost Function(Loss Function)}}$,是将随机事件或其有关随机变量的取值映射为非负实数以表示该随机事件的“损失”的函数。在应用中,损失函数通常作为学习准则与优化问题相联系,即通过最小化损失函数求解和评估模型。例如在机器学习中被用于模型的$\mathop{\text{参数估计}}\limits_{\texttt{Parameteric Estimation}}