DP 学习笔记(三):与斜率有关的 DP 优化
orange_new · · 算法·理论
几何无王者之道,惟有点与线之舞蹈。————笛卡尔
几何不光只有中考高考考的那三瓜两枣,在 DP 中也可以有非常重要的作用。
基础知识
斜率
函数的凹凸性
凸壳
斜率优化
这种优化算是后面要讲的决策单调性的特殊情况,不过没有决策单调性的性质也可以做。
P2900 [USACO08MAR] Land Acquisition G
P4360 [CEOI 2004] 锯木厂选址
P3628 [APIO2010] 特别行动队
四边形不等式优化
应用场合
对于区间 DP,我们一般需要枚举一段区间的分割点,把当前区间拆分成两个小区间,把两个小区间的答案加起来再加上这两个区间合在一起的代价,也就是
四边形不等式的定义
我们先给出四边形不等式的定义:设
为什么这个叫做四边形不等式,我们考虑将这四个区间画在数轴上:
我们把
此时我们要证明
在
下面再给出二元函数单调性的定义:如果对于任意整数
四边形不等式定理
我们先来一些定义,我们设二元函数
这个
这里的二元函数
下面,我们先来证明两个引理。
引理 2.3.1
如果
证明:
分以下
-
-
我们设 $c(i, j')$ 在 $k = z$ 处有最小值,记为 $c_z(i, j) = c(i, j) = w(i, j) + c(i, z) + c(z + 1, j)$。 现在有两个对称的情况,$z \leq j$ 和 $z \geq j$,我们只证明 $z \leq j$ 的情况,$z \geq j$ 同理可得。 考虑数学归纳法,我们先证明 $z \leq j \leq j'$ 时引理成立,此时我们设三角形三个顶点分别是 $i, j, j'$,它们之间的边长分别是 $c(i, j), c(j, j'), c(i, j')$,那么 $z$ 就是 $ij'$ 这条边上的一个最优分割点,于是我们可以画出下图: 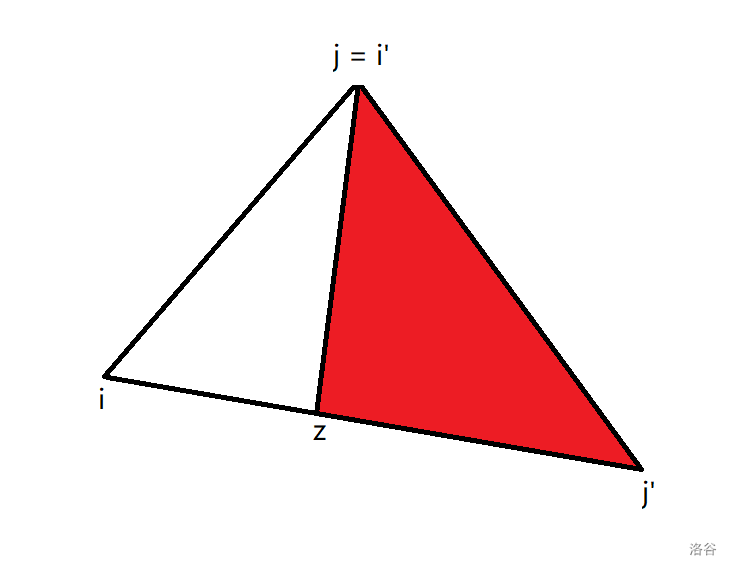 在 $\triangle zjj'$ 中,$c(z, j) + c(j, j') \leq c(z + 1, j')$,这是反三角不等式此时满足引理 2.3.1。 我们考虑,$z$ 为 $i$ 到 $j'$ 的区间最优分割点,但有可能是 $i$ 到 $j'$ 的最优分割点,因此 $c(i, j) \leq c_z(i, j) = w(i, j) + c(i, z) + c(z + 1, j)$。 我们把两边同时加上 $c(j, j')$,可以得到 $c(i, j) + c(j, j') \leq w(i, j) + c(i, z) + c(z + 1, j) + c(j, j')$。由于单调性 $w(i, j) \leq w(i, j')$,而根据之前求出的不等式 $c(z, j) + c(j, j') \leq c(z, j')$,可以得出 $c(i, j) + c(j, j') \leq w(i, j') + c(i, z) + c(z + 1, j') = c(i, j')$。 - $i < i' < j < j'$,此时是最普通的情况。假设小区间 $c(i', j)$ 和大区间 $c(i, j')$ 分别在 $k = y$ 和 $k = z$ 处取得最小值,记为 $c(i', j) = c_y(i', j) = w(i', j) + c(i', y) + c(y + 1, j)$,$c(i, j') = c_z(i, j') = w(i, j') + c(i, z) + c(z + 1, j')$。 现在又有两个对称的情况,$z \leq y$ 和 $z \geq y$,我们只证明 $z \leq y$ 的情况,$z \geq y$ 同理可得。 我们依然考虑数学归纳法,先证明边界情况,即 $z \leq y < j < j'$ 时引理成立。我们设四边形的四个顶点是 $i, i', j, j'$,它们之间的边长分别是 $c(i, j'), c(j, j'), c(i', j), c(i, i')$,那么 $y$ 就是 $i'j$ 这条边上的最优分割点,而 $z$ 就是 $ij'$ 这条边上的最优分割点,于是我们可以画出下图: 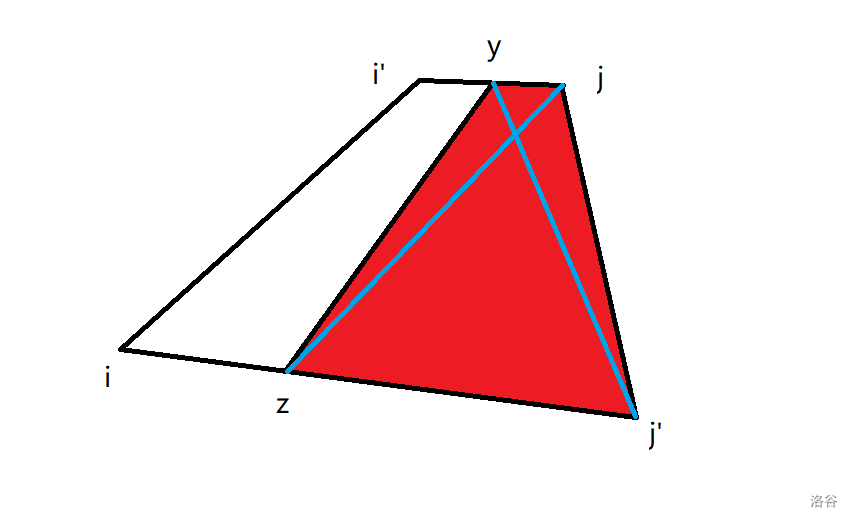 根据四边形不等式,$c(z, j) + c(y, j) \leq c(y + 1, j) + c(z + 1, j')$,此时满足引理 2.3.1。 依然考虑 $y$ 是 $i'$ 到 $j$ 的最优分割点,可能是 $i'$ 到 $j'$ 的最优分割点,因此 $c(i', j') \leq c_z(i', j')$,同理可得 $c(i, j) \leq c_z(i, j)$,于是将等式左边加起来,等式右边加起来,可以得到 $c(i, j) + c(i', j') \leq c_z(i, j) + c_y(i', j') = w(i, j) + w(i', j') + c(i, z) + c(z + 1, j) + c(i', y) + c(y + 1, j')$。 根据 $w$ 的单调性以及推出的 $c(z, j) + c(y, j) \leq c(y + 1, j) + c(z + 1, j')$,可以得到 $c(i, j) + c(i', j') \leq w(i', j) + w(i, j') + c(i, z) + c(i', y) + c(y + 1, j) + c(z + 1, j') = c(i', j) + c(i, j')$。
现在就证明了引理 2.3.1。
引理 2.3.2
用
证明:
当
我们先证明
根据引理 2.3.1 的结论,若
我们把不等式两边同时加上
由于我们有
定理 2.3.1(四边形不等式定理)
现在开始证明最主要的这个定理了。
四边形不等式定理的内容是,用 DP 计算所有
证明:
我们计算区间 DP 时,一般都是枚举区间长度,再枚举左端点,也就是按照
将等式左边加在一起,右边加在一起,那么总枚举次数就是
当求的东西从
应用
其实在真正的比赛中,一般都是打表发现单调性与四边形不等式就直接用了,但在此处还是证明一下吧。
P1880 [NOI1995] 石子合并
这道题目在区间 DP 时已经讲过了,但是可以用四边形不等式进一步优化成
我们已知它的 DP 转移方程是
但是我们要求最大值时,发现
完整代码:
#include <bits/stdc++.h>
using namespace std;
const int N = 2e2 + 9;
int n, a[N], dp[N][N], dp2[N][N], s[N][N], num[N], ans1 = 100000000, ans2 = 0;
int main(){
scanf("%d", &n);
for(int i = 1; i <= n; i++){
scanf("%d", &a[i]);
num[i] = num[i - 1] + a[i];
}
for(int i = 1; i <= n - 1; i++)
num[i + n] = num[i + n - 1] + a[i];
n = n * 2 - 1;
for(int i = 1; i <= n; i++)
s[i][i] = i;
for(int len = 2; len <= n; len++){
for(int i = 1; i <= n - len + 1; i++){
int j = i + len - 1;
dp[i][j] = 100000000;
for(int k = s[i][j - 1]; k <= s[i + 1][j]; k++)
if(dp[i][k] + dp[k + 1][j] + num[j] - num[i - 1] < dp[i][j]){
dp[i][j] = dp[i][k] + dp[k + 1][j] + num[j] - num[i - 1];
s[i][j] = k;
}
dp2[i][j] = max(dp2[i][j - 1], dp2[i + 1][j]) + num[j] - num[i - 1];
}
}
n = (n + 1) / 2;
for(int i = 1; i <= n; i++){
ans1 = min(ans1, dp[i][n + i - 1]);
ans2 = max(ans2, dp2[i][n + i - 1]);
}
printf("%d\n%d", ans1, ans2);
return 0;
} UVA10304 Optimal Binary Search Tree
这就是四边形不等式优化的来源。
其实这道题目和石子合并特别像,如果我们把合并过程看成一棵树,那么每堆石子的贡献就是石子的个数乘以这堆石子的深度,因此我们有类似的 DP 优化方法。
我们设
完整代码:
#include <bits/stdc++.h>
using namespace std;
#define int long long
const int N = 259;
int dp[N][N], s[N][N], sum[N], a[N], n;
signed main(){
while(~scanf("%lld", &n) && n){
memset(s, 0, sizeof(s));
memset(dp, 0x3f, sizeof(dp));
for(int i = 1; i <= n; i++){
scanf("%lld", &a[i]);
sum[i] = sum[i - 1] + a[i];
s[i][i] = i;
dp[i][i] = dp[i + 1][i] = dp[i][i - 1] = 0;
}
for(int len = 2; len <= n; len++){
for(int i = 1; i + len - 1 <= n; i++){
int j = i + len - 1;
for(int k = s[i][j - 1]; k <= s[i + 1][j]; k++){
if(dp[i][j] > dp[i][k - 1] + dp[k + 1][j] + sum[j] - sum[i - 1] - a[k]){
dp[i][j] = dp[i][k - 1] + dp[k + 1][j] + sum[j] - sum[i - 1] - a[k];
s[i][j] = k;
}
}
}
}
printf("%lld\n", dp[1][n]);
}
return 0;
}P4767 [IOI 2000] 邮局 加强版
为什么是先出加强版再出普通版????
我们设
现在我们来分析
由于本题不是一般的区间 DP,我们求
完整代码:
#include <bits/stdc++.h>
using namespace std;
#define int long long
const int N = 3e2 + 9, M = 3e3 + 9;
int a[M], dis[M][M], f[M][N], s[M][N], n, m;
signed main(){
scanf("%lld%lld", &n, &m);
for(int i = 1; i <= n; i++)
scanf("%lld", &a[i]);
for(int i = 1; i <= n; i++){
dis[i][i] = 0;
for(int j = i + 1; j <= n; j++)
dis[i][j] = dis[i][j - 1] + a[j] - a[(i + j) >> 1];
}
memset(f, 0x3f, sizeof(f));
f[0][0] = 0;
for(int j = 1; j <= m; j++){
s[n + 1][j] = n;
for(int i = n; i >= 1; i--)
for(int k = s[i][j - 1]; k <= s[i + 1][j]; k++)
if(f[i][j] > f[k][j - 1] + dis[k + 1][i]){
f[i][j] = f[k][j - 1] + dis[k + 1][i];
s[i][j] = k;
}
}
printf("%lld", f[n][m]);
return 0;
}P4072 [SDOI2016] 征途
这道题目和上一道,都是将
我们设第
将平方展开,可以得到原式
乘以
此时我们就可以开始 DP 了,设
现在的价值函数变成了
将两边的式子拆开,可以得到
完整代码:
#include <bits/stdc++.h>
using namespace std;
#define int long long
const int N = 3e3 + 2;
int a[N], sum[N], f[N][N], s[N][N], n, m;
signed main(){
scanf("%lld%lld", &n, &m);
for(int i = 1; i <= n; i++){
scanf("%lld", &a[i]);
sum[i] = sum[i - 1] + a[i];
}
memset(f, 0x3f, sizeof(f));
f[0][0] = 0;
for(int j = 1; j <= m; j++){
s[n + 1][j] = n;
for(int i = n; i >= 1; i--)
for(int k = s[i][j - 1]; k <= s[i + 1][j]; k++)
if(f[i][j] > f[k][j - 1] + (sum[i] - sum[k]) * (sum[i] - sum[k])){
f[i][j] = f[k][j - 1] + (sum[i] - sum[k]) * (sum[i] - sum[k]);
s[i][j] = k;
}
}
printf("%lld", f[n][m] * m - sum[n] * sum[n]);
return 0;
}拓展:\text{Garsia-Wachs} 算法
P5569 [SDOI2008] 石子合并
决策单调性优化
DP 也是一种数据结构,它维护了数组。———— hfu
这在决策单调性中很有体现。
应用场合
其实,我们之前做P4767 [IOI 2000] 邮局 加强版时已经发现它不再是标准的区间 DP 了,如果去掉邮局的个数限制,那么这道题就变成了一维的 DP。当
对于形如
证明:
对于
另一种决策单调性:对于形如
证明:
对于
应用
运用决策单调性可以把形如
二分队列
此做法适用于价值函数满足交叉优于包含,且求
我们维护一个队列,其中每个元素都是三元组
我们枚举每个
不过还有一点,就是分割点可以在某段
此外,如果一个决策点
P1912 [NOI2009] 诗人小G
白日依山尽,黄河入海流。
欲穷千里目,更上一层楼。————题目样例
我们设
这又是这种区间划分的形式,由于有
那么现在,我们需要证明
观察两边式子的形式,可以用
由于含有绝对值,因此我们用零点分段法来证明:
此时我们证明了该函数单调递减,从而证明了四边形不等式。
完整代码:
#include <bits/stdc++.h>
using namespace std;
#define int long long
const int N = 3e6 + 5, INF = 1e18;
int read(){
int x = 0, f = 1;
char ch = getchar();
while(!isdigit(ch)){
if(ch == '-')
f = -1;
ch = getchar();
}
while(isdigit(ch)){
x = (x << 1) + (x << 3) + (ch ^ 48);
ch = getchar();
}
return x * f;
}
struct Node{
int l, r, pos;
} q[N];
int s[N], pre[N], n, L, k, T, head, tail;
char poem[N][31];
bool flag[N];
long double dp[N];
long double qpow(long double a, int b){
long double res = 1;
while(b > 0){
if(b & 1)
res = res * a;
a = a * a;
b >>= 1;
}
return res;
}
long double w(int j, int i){
return dp[j] + qpow(abs(s[i] - s[j] + i - j - 1 - L), k);
}
int bs(int id, int x){
int res = q[id].r, l = q[id].l, r = q[id].r;
while(l <= r){
int mid = (l + r) >> 1;
if(w(q[id].pos, mid) >= w(x, mid)){
res = mid;
r = mid - 1;
} else
l = mid + 1;
}
return res;
}
void insert(int i){
if(head <= tail && q[head].r < i)
head++;
else
q[head].l = i;
if(dp[i] > w(q[head].pos, i)){
dp[i] = w(q[head].pos, i);
pre[i] = q[head].pos;
}
while(head <= tail && w(i, q[tail].l) <= w(q[tail].pos, q[tail].l))
tail--;
if(head > tail)
q[++tail] = Node{i, n, i};
else if(w(i, q[tail].r) >= w(q[tail].pos, q[tail].r)){
if(q[tail].r == n)
return;
q[tail + 1] = Node{q[tail].r + 1, n, i};
tail++;
} else {
int p = bs(tail, i);
q[tail].r = p - 1;
q[++tail] = Node{p, n, i};
}
}
signed main(){
T = read();
while(T--){
for(int i = 1; i <= n; i++){
dp[i] = 0;
pre[i] = 0;
flag[i] = 0;
}
for(int i = 1; i <= tail; i++)
q[i] = Node{0, 0, 0};
n = read();
L = read();
k = read();
for(int i = 1; i <= n; i++){
scanf("%s", poem[i]);
s[i] = s[i - 1] + strlen(poem[i]);
dp[i] = w(0, i);
}
head = 1;
tail = 0;
for(int i = 1; i <= n; i++)
insert(i);
if(dp[n] > 1e18)
printf("Too hard to arrange\n");
else {
printf("%.0Lf\n", dp[n]);
for(int i = n; i; i = pre[i])
flag[i] = true;
for(int i = 1; i <= n; i++){
printf("%s", poem[i]);
if(flag[i])
printf("\n");
else
printf(" ");
}
}
printf("--------------------\n");
}
return 0;
}P3515 [POI 2011] Lightning Conductor
我们设
我们现在要证明
我们构造函数
完整代码:
#include <bits/stdc++.h>
using namespace std;
const int N = 5e5 + 9;
struct Node{
int l, r, pos;
} q[N];
int h[N], n, head, tail;
double dp[N];
double w(int j, int i){
return h[j] + sqrt((i - j) * 1.0);
}
int bs(int id, int x){
int res = q[id].r + 1, l = q[id].l, r = q[id].r;
while(l <= r){
int mid = (l + r) >> 1;
if(w(q[id].pos, mid) <= w(x, mid)){
res = mid;
r = mid - 1;
} else
l = mid + 1;
}
return res;
}
void insert(int i){
if(head <= tail && q[head].r < i)
head++;
else
q[head].l = i;
dp[i] = max(dp[i], w(q[head].pos, i));
while(head <= tail && w(i, q[tail].l) >= w(q[tail].pos, q[tail].l))
tail--;
if(head > tail)
q[++tail] = Node{i, n, i};
else if(w(i, q[tail].r) <= w(q[tail].pos, q[tail].r)){
if(q[tail].r == n)
return;
q[tail + 1] = Node{q[tail].r + 1, n, i};
tail++;
} else {
int p = bs(tail, i);
q[tail].r = p - 1;
q[++tail] = Node{p, n, i};
}
}
int main(){
scanf("%d", &n);
for(int i = 1; i <= n; i++){
scanf("%d", &h[i]);
dp[i] = h[i];
}
head = 1;
tail = 0;
for(int i = 1; i <= n; i++)
insert(i);
for(int i = 1; i <= n / 2; i++){
swap(h[i], h[n - i + 1]);
swap(dp[i], dp[n - i + 1]);
}
head = 1;
tail = 0;
for(int i = 1; i <= n; i++)
insert(i);
for(int i = n; i >= 1; i--)
printf("%d\n", int(ceil(dp[i]) - h[i]));
return 0;
}二分栈
此做法适用于价值函数满足交叉大于包含,且求
和二分队列很像,只是这次我们维护的是栈,因为栈满足先进后出,那么越先进入的点就越有可能成为越后进入的点的决策点。
我们依然枚举每个
P5504 [JSOI2011] 柠檬
我们设
于是我们每种颜色分开考虑。此时的价值函数是
完整代码:
#include <bits/stdc++.h>
using namespace std;
#define int long long
const int N = 1e5 + 9;
struct Node{
int l, r, pos;
};
vector <int> mp[N];
vector <Node> st[N];
int s[N], dp[N], cnt[N], rk[N], n;
int w(int j, int i, int c){
return dp[mp[c][j] - 1] + (i - j + 1) * (i - j + 1) * c;
}
int bs(int x, int c){
int res = st[c].back().l, l = st[c].back().l, r = st[c].back().r;
while(l <= r){
int mid = (l + r) >> 1;
if(w(st[c].back().pos, mid, c) >= w(x, mid, c)){
res = mid;
r = mid - 1;
} else
l = mid + 1;
}
return res;
}
void insert(int i, int c){
while(!st[c].empty() && w(i, st[c].back().r, c) >= w(st[c].back().pos, st[c].back().r, c))
st[c].pop_back();
if(st[c].empty())
st[c].push_back(Node{i, cnt[c], i});
else if(w(i, st[c].back().l, c) <= w(st[c].back().pos, st[c].back().l, c)){
if(st[c].back().l != i)
st[c].push_back(Node{i, st[c].back().l - 1, i});
} else {
int p = bs(i, c);
st[c].back().l = p;
st[c].push_back(Node{i, p - 1, i});
}
if(!st[c].empty() && st[c].back().r < i)
st[c].pop_back();
else
st[c].back().l = i;
dp[mp[c][i]] = w(st[c].back().pos, i, c);
}
signed main(){
scanf("%lld", &n);
for(int i = 1; i <= n; i++){
scanf("%lld", &s[i]);
rk[i] = ++cnt[s[i]];
if(cnt[s[i]] == 1)
mp[s[i]].push_back(0);
mp[s[i]].push_back(i);
}
for(int i = 1; i <= n; i++)
insert(rk[i], s[i]);
printf("%lld", dp[n]);
return 0;
}分治
这也是一种常见的决策单调性优化 DP 的写法,而且比单调队列还好理解,我们设 DP(int l, int r, int ql, int qr) 表示当前要计算
每次我们暴力算出区间中点处的 DP 值,并记录它的决策点,那么左区间的决策点一定在当前决策点左边,右区间的决策点一定在当前决策点右边,此时就可以分治往下做了。
不过分治并不能解决一切决策单调性问题,它只能解决一层一层 DP 的问题,如果不是一层一层解决问题,很有可能当前分治中心的决策点的 DP 值还没有算出,导致程序出现问题。
P5574 [CmdOI2019] 任务分配问题
这道题目就是典型的区间拆分问题,DP 方程就是经典的
我们现在要证明
还有一点,这道题区间的贡献不能
完整代码:
#include <bits/stdc++.h>
using namespace std;
#define int long long
const int N = 2.5e4 + 9, K = 29;
int a[N], dp[N][K], n, m;
int t[N];
int lowbit(int x){
return x & -x;
}
void insert(int i, int x){
for(; i <= n; i += lowbit(i))
t[i] += x;
}
int ask(int i){
int res = 0;
for(; i > 0; i -= lowbit(i))
res += t[i];
return res;
}
int L = 1, R, ans;
int w(int l, int r){
while(l < L){
ans += R - L + 1;
ans -= ask(a[--L]);
insert(a[L], 1);
}
while(R < r){
ans += ask(a[++R]);
insert(a[R], 1);
}
while(L < l){
insert(a[L], -1);
ans += ask(a[L++]);
ans -= R - L + 1;
}
while(r < R){
insert(a[R], -1);
ans -= ask(a[R--]);
}
return ans;
}
void dac(int l, int r, int ql, int qr, int k){
if(l > r)
return;
int mid = (l + r) >> 1, pos = ql;
dp[mid][k] = 0x3f3f3f3f;
for(int i = ql; i <= min(qr, mid); i++)
if(dp[i - 1][k - 1] + w(i, mid) < dp[mid][k]){
dp[mid][k] = dp[i - 1][k - 1] + w(i, mid);
pos = i;
}
dac(l, mid - 1, ql, pos, k);
dac(mid + 1, r, pos, qr, k);
}
int res = 0x3f3f3f3f;
signed main(){
scanf("%lld%lld", &n, &m);
for(int i = 1; i <= n; i++)
scanf("%lld", &a[i]);
for(int i = 1; i <= n; i++)
dp[i][0] = 0x3f3f3f3f;
for(int j = 1; j <= m; j++){
dac(1, n, 1, n, j);
res = min(res, dp[n][j]);
}
printf("%lld", res);
return 0;
}CF868F Yet Another Minimization Problem
这道题目和上一道基本一样,转移方程还是
我们此处还是要证明
完整代码:
#include <bits/stdc++.h>
using namespace std;
#define int long long
const int N = 1e5 + 9, K = 21, INF = 1e18;
int a[N], dp[N][K], n, m;
int cnt[N];
int L = 1, R, ans;
int w(int l, int r){
while(l < L){
ans += cnt[a[--L]];
cnt[a[L]]++;
}
while(R < r){
ans += cnt[a[++R]];
cnt[a[R]]++;
}
while(L < l){
cnt[a[L]]--;
ans -= cnt[a[L++]];
}
while(r < R){
cnt[a[R]]--;
ans -= cnt[a[R--]];
}
return ans;
}
void dac(int l, int r, int ql, int qr, int k){
if(l > r)
return;
int mid = (l + r) >> 1, pos = ql;
dp[mid][k] = INF;
for(int i = ql; i <= min(qr, mid); i++)
if(dp[i - 1][k - 1] + w(i, mid) < dp[mid][k]){
dp[mid][k] = dp[i - 1][k - 1] + w(i, mid);
pos = i;
}
dac(l, mid - 1, ql, pos, k);
dac(mid + 1, r, pos, qr, k);
}
int res = INF;
signed main(){
scanf("%lld%lld", &n, &m);
for(int i = 1; i <= n; i++)
scanf("%lld", &a[i]);
for(int i = 1; i <= n; i++)
dp[i][0] = INF;
for(int j = 1; j <= m; j++){
dac(1, n, 1, n, j);
res = min(res, dp[n][j]);
}
printf("%lld", res);
return 0;
}CF833B The Bakery
这道题基本上算是上一道题目的双倍经验了,证法不再赘述。
完整代码:
#include <bits/stdc++.h>
using namespace std;
#define int long long
const int N = 3.5e4 + 9, K = 59;
int a[N], dp[N][K], n, m;
int cnt[N];
int L = 1, R, ans;
int w(int l, int r){
while(l < L){
cnt[a[--L]]++;
if(cnt[a[L]] == 1)
ans++;
}
while(R < r){
cnt[a[++R]]++;
if(cnt[a[R]] == 1)
ans++;
}
while(L < l){
if(cnt[a[L]] == 1)
ans--;
cnt[a[L++]]--;
}
while(r < R){
if(cnt[a[R]] == 1)
ans--;
cnt[a[R--]]--;
}
return ans;
}
void dac(int l, int r, int ql, int qr, int k){
if(l > r)
return;
int mid = (l + r) >> 1, pos = ql;
for(int i = ql; i <= min(qr, mid); i++)
if(dp[i - 1][k - 1] + w(i, mid) > dp[mid][k]){
dp[mid][k] = dp[i - 1][k - 1] + w(i, mid);
pos = i;
}
dac(l, mid - 1, ql, pos, k);
dac(mid + 1, r, pos, qr, k);
}
int res;
signed main(){
scanf("%lld%lld", &n, &m);
for(int i = 1; i <= n; i++)
scanf("%lld", &a[i]);
for(int j = 1; j <= m; j++){
dac(1, n, 1, n, j);
res = max(res, dp[n][j]);
}
printf("%lld", res);
return 0;
}线段树分治 + 分治
P5244 [USACO19FEB] Mowing Mischief P
总结
二维 DP 可以用四边形不等式优化的条件:
-
求
\min ,价值函数满足交叉优于包含,且大区间的权值大于小区间的权值; -
求
\max ,价值函数满足包含优于交叉,且大区间的权值小于小区间的权值。
一维 DP 可以用二分队列优化:
-
求
\min ,价值函数满足交叉优于包含; -
求
\max ,价值函数满足包含优于交叉。
一维 DP 可以用二分栈优化:
-
求
\min ,价值函数满足包含优于交叉; -
求
\max ,价值函数满足交叉优于包含。
WQS 二分
应用场合
当上述决策单调性题目的
WQS 二分主要解决从
这类问题的难点在于只能选
拿求最大值来举例子,如果没有
假设原先的 DP 函数构成的凸包长这个样子:
那么我们的答案就是
主流博客中都说是拿一条直线去切这个凸壳,但是我觉得这样并不直观,于是我换了一种方法理解。我们将这个凸壳进行旋转,比如旋转到以下的情况:
(
此时我们发现整个凸壳的最高点从
此时上凸壳的作用就凸显了出来,那就是整个凸包在旋转过程中,最大值不断在减小。因此我们可以二分
凸性判断
其实这东西比赛的时候一般感性理解就可以了,严格证明一般比较困难。但是还是有方法的。下面我们先给出一道例题,分别用不同的方法证明它的凸性。
有
简言之,就是在长度为
应用
P5633 最小度限制生成树
这就是一道典型的 WQS 二分的题目。
如果没有满足编号为
P6246 [IOI 2000] 邮局 加强版 加强版
P4383 [八省联考 2018] 林克卡特树
AT_arc168_e Subsegments with Large Sums
Slope Trick
-
黄 kx、付 ym、吴 g 的课件
-
算法竞赛 罗勇军、郭卫斌
-
算法竞赛进阶指南 李煜东
-
决策单调性 JueFan
-
[POI2011]Lightening Conductor(决策单调性) ATS_nantf
-
DP的决策单调性优化总结 command_block
-
关于WQS二分算法以及其一个细节证明 Creeper_LKF
-
【学习笔记】WQS二分详解及常见理解误区解释 ikrvxt
-
wqs二分 花子の水晶植轮daisuki
-
WQS 二分 凸性证明 OI Wiki