DP...
Lywh_ddAC
·
·
算法·理论
不是?信息学这么久了,才想起来好好理解一下动态规划?
讲了那么久dp优化半句不懂,才想起来要补一下dp?
首先先记住,dp题的解题思路通常为:
读懂题意,设计状态,确定目标态和初始态,思考转移方程,思考优化。
OI Wiki
初学dp题单,中型dp题单
一个一个来吧
线性dp
一维dp,多做两道题就能get到。
B3636 文字工作,B3635 硬币问题 ,P2842 纸币问题 1
好吧有人说这也算线性dp:
SP15637 GNYR04H - Mr Youngs Picture Permutations
背包
01背包
就是先枚举物品,再枚举时间,按照常用的一维写法,要注意时间要倒着枚举,不然有可能会错用本次修改的值。
至于为什么先枚举物品,再枚举时间,就能保证一个物体只选一次呢,会发现针对每一个dp[j],v[i]始终只会加一次。
例题:P1926 小书童——刷题大军
for(int i=1;i<=m;i++){//针对前i个作业
for(int j=r;j>=1;j--){//花j的时间
if(j>=w[i])
dp[j]=max(dp[j],dp[j-w[i]]+v[i]);
}
}
当然,不要压缩的话就要继承:
for(int i=1;i<=m;i++){//针对前i个作业
for(int j=1;j<=r;j++){//花j的时间
if(j>=w[i])
dp[i][j]=max(dp[i-1][j],dp[i-1][j-w[i]]+v[i]);//继承上边
//可以保证dp[i-1][l~r]是一定没有加过v[i]的
}
}
注意,压缩是常用的手段,用来减少空间负担,如果不的话,有几个限制条件就需要定义几维。
完全背包
不同理,先枚举时间,再枚举物品,为的就是能在相同时间下重复计算。
例题:P1616 疯狂的采药
for(int i=1;i<=t;i++){//先枚举时间
for(int j=1;j<=m;j++){//再枚举物品
if(i-a[j]>=0)
dp[i]=max(dp[i],dp[i-a[j]]+b[j]);
}
}
同样的,转移方程也能压缩,但这时时间就要正着枚举了,因为就是要重复计算。
数位dp
都说数位dp简单,没想到现在为止,才做了两道真正意义上的数位dp的题?
例题:P4124 [CQOI2016] 手机号码
很清新的题解,感觉应该看看就能明白:题解
数位dp较其他dp不同的一点在于,它一般是由记忆化搜索实现的,确实没有什么思维上需要跨越的东西,一般就是实现起来考码力,有的大佬写的就很简洁,有的就很冗长(不是我)。
唯一有一点初学可能会顿的地方就是,一般都会有一个判断是否严格小于或者是否顶格的东西,其实也不难理解。
比如从前往后对于每一个数位填数时,为了不超出限定范围,如果此位以前有高位(至少一位)是小于同位的上线的,那么这一位填啥都可以(不会超范围),但如果以前的所有位数都是顶着上限开的,那么此位就一定不能超过当前位的上限。
状压dp
例题:P3052 [USACO12MAR] Cows in a Skyscraper G
还能理解的一篇题解,题解 P3052
像这种普通dp写不出来的,数据范围又不是太大的,可以想到状压dp。
针对每一个状态,尝试去加每一个牛(不在状态里的)。$size[i]$ 表示的是,已经运输牛状态为 $i$ (二进制下),最后一个电梯剩余的最大容量(全局最大)。
怎样在每个状态下加牛呢?假设加第 $j$ 个牛,$dp[i|(1<<(j-1))]$ 从 $dp[i]$ 而来,那么所用的电梯数就看,$size[i]$ 是否大于 $c[j]$(装不装得下),能装下就直接继承,更改 $size$,不能的话,$dp[i|(1<<(j-1))]$ 就等于 $dp[i]+1$,更改 $size$。
$size$ 数组只记录最后一个电梯的剩余容量,是否会导致无法利用之前电梯的剩余空间?
不会,因为每个 $dp$ 都是由状态继承过来的,相应的 $size$ 也会继承,$dp$ 会保留所有可能方案中最优的那个,$size$ 也一样,它会保证到达状态 $i$ 所剩的电梯空间最多。
::::info[举例 ]
电梯容量 W=8
三头牛的重量:4、5、4。
加入牛1(重4):
新状态,001,由于初始电梯为空,牛1可以放入,所以:
dp[001] = 1,size[001] = 4
加入牛2(重5):
从状态001出发,尝试将牛2加入:
检查当前电梯剩余容量:size[001]<5,
放不下,需要新开电梯:dp[011]=dp[001]+1=2,新电梯装载牛2,size=4此时状态011所以:
dp[011] = 2,size[011] = 3
但是,**这不是到达状态011的唯一方式**!我们还可以先装牛2再装牛1:
从初始状态直接装牛2:
状态010,dp[010]=1,size[010]=5,
然后加入牛1:检查size[010]<4,放不下,新开电梯
得到状态011:
dp[011] = 2,size[011]=4
在DP过程中,当两种方式都达到状态011时,我们会比较:
电梯数量相同(都是2),但第二种方式的size更大
因此,DP会选择第二种方式:
dp[011]=2,size[011]=4。
::::
一道橙题,在这哔哔这么久?我还是太菜了,具体的:
```cpp
for(int i=0;i<=(1<<n)-1;i++)//枚举状态
for(int j=1;j<=n;j++){
if((1<<(j-1))&i) continue ;
if(size[i]>=c[j]){//塞的下
if(dp[i]<=dp[i|(1<<(j-1))]){
dp[i|(1<<(j-1))]=dp[i];
size[i|(1<<(j-1))]=max(size[i|(1<<(j-1))],size[i]-c[j]);
}
}
else{//塞不下
if(dp[i]+1<=dp[i|(1<<(j-1))]){
dp[i|(1<<(j-1))]=dp[i]+1;
size[i|(1<<(j-1))]=max(size[i|(1<<(j-1))],w-c[j]);
}
}
}
```
练习:[CF453B Little Pony and Harmony Chest](https://www.luogu.com.cn/problem/CF453B)
自己的题解!:[题解](https://www.luogu.com.cn/article/nut6yqln)
## 插头dp
对于插头dp,个人理解是一种和状压dp像(写完了才发现其实一点都不一样...只是有时能互相转换罢了),时间复杂度比其更优秀,状态转移支持更复杂,适用于解决网格联通性问题的一种强大dp。
例题:[P10975 Mondriaan's Dream](https://www.luogu.com.cn/problem/P10975)
(都写完了才发现这道题对插头的体现好像不是太明显...)
### 状压
还算详细的题解:[题解](https://www.luogu.com.cn/article/gvf9ufjo)。
当然,它对状态的定义有错......在评论区纠正了。
有锅的地方:关于压缩状态的定义,对于一行的状态,
- $1$ 表示当前位置是一个**竖着骨牌的上半部分**。
- $0$ 表示其他可能的情况,包括一张竖着骨牌的下半部分,或者一张横骨牌的一部分。
其余的题解里讲得很清楚了,在此不多赘述。
发现其时间复杂度为 $O(h×4^w)$。不是很优,于是引出更优秀的插头dp。
### 插头
如果真正搞懂了插头dp,就会发现其实它的另一个名字更能体现出他的实现特点,**轮廓线dp**,它的实质就是在**维护一条轮廓线的状态**。
对于这道题,它会对于每一个点 $(i,j)$ 枚举所有的经过点 $(i,j)$ 的轮廓线状态。
#### 一个问题,什么是轮廓线?
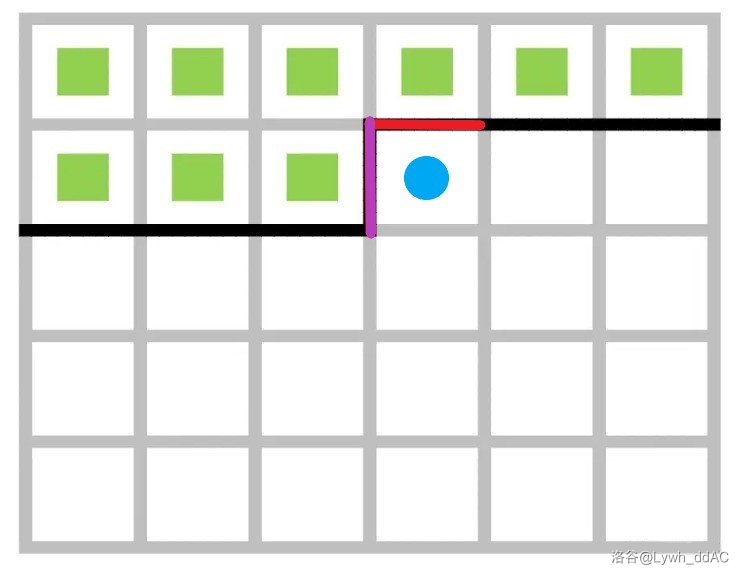
图中黑(红、紫)色的那一条线就是**轮廓线**,可以发现,轮廓线包含了m条横边和一条竖边。在代码中,他被抽象成一串长度为m+1的二进制数。
如果一段轮廓线有值,就表示那上面有一个插头,需要对接。比如如果图中紫色的那条边有值,那么表明蓝点左边的点有一个向右的插头,从而当前蓝点就必须有一个状态向左的插头,按例题来讲就是说,蓝点左边有一个骨牌横着放,其右半部分在蓝点上,所以蓝点就只能放置骨牌的右半部分。其上的红色轮廓线也是同理,轮廓线dp会针对每一个位置,枚举所有状态的轮廓线,(轮廓线的形状不变,状态单指值这点和状压dp一样)。
#### 那怎么用轮廓线计算答案呢?
$dp[cur][s]$ 表示对于第 $i$ 个点,能拼到轮廓线状态为 $s$ 的方法有多少种。
对于一个 $dp[cur][s]$ 而言,$s$ 如果可以通过当前决策,得到新的状态 $news$,那么 $news$ 的方案数要加上 $dp[cur][s]$。
具体的看这个:[轮廓线 dp 题解](https://www.luogu.com.cn/article/on78c6ew)
关于他的上下行初始化有点难懂,但我在代码里注释了,反正我现在是懂了...
这样它的复杂度就到了 $O(hw2^w)$,是优化了不少。
::::info[代码]
```cpp
#include<bits/stdc++.h>
using namespace std;
#define N 20
#define int long long
int h,w,cur;
int dp[5][1<<15];
signed main(){
while(cin>>h>>w&&(h!=0||w!=0)){
memset(dp,0,sizeof(dp));
dp[0][0]=1;
cur=0;
for(int i=1;i<=h;i++){
cur^=1;
memset(dp[cur],0,sizeof(dp[cur]));
/*当上一行向下一行转移时,要将s变为0~~~~,
这个(~~~~)就是上一行实际网格1到w位的状态
(相当于不算最后一位竖着的,因为只有w位啊)
,的形式,代码位数于实际网格情况刚好相反,也就是一定是~~~~0*/
for(int j=0;j<(1<<w);j++){
dp[cur][j<<1]=dp[cur^1][j];
}
for(int j=1;j<=w;j++){
cur^=1;
memset(dp[cur],0,sizeof(dp[cur]));
for(int s=0;s<(1<<(w+1));s++){//当前轮廓线
int left=(s>>(j-1))&1,up=(s>>j)&1;
int new_s;
/*有dp[i-1][s]种方法可以铺到当前new_s状态*/
if(left&&up) continue ;
if(left&&!up){//左边有,上边没有
new_s=s-(1<<(j-1));//把左边的消掉
dp[cur][new_s]+=dp[cur^1][s];
}
if(!left&&up){//左边没有,上边有
new_s=s-(1<<j);
dp[cur][new_s]+=dp[cur^1][s];
}
if(!left&&!up){//左右都没有
new_s=s+(1<<j);
dp[cur][new_s]+=dp[cur^1][s];
new_s=s+(1<<(j-1));
dp[cur][new_s]+=dp[cur^1][s];
}
}
}
}
cout<<dp[cur][0]<<endl;
}
return 0;
}
```
::::
真正的例题:[P5074 Eat the Trees](https://www.luogu.com.cn/problem/P5074)
## dp优化
终于到优化了。
看不懂的:[dp 优化](https://www.luogu.com.cn/article/oj8m8l9y)
### 单调队列
这算很常见的一种优化了,
例题:[P3572 [POI 2014] PTA-Little Bird](https://www.luogu.com.cn/problem/P3572)
首先想到朴素的dp写法:
```cpp
for(int i=1;i<=n;i++){
for(int j=max(1ll,i-k);j<=i;j++){
if(d[j]<=d[i]) dp[i]=min(dp[i],dp[j]+1);
else dp[i]=min(dp[i],dp[j]);
}
}
```
就是对于每个位置 $i$,找它前面 $k$ 个 $dp$ 值对它的贡献,数据范围告诉我们要优化。
**为什么选用单调队列**?或者说,为什么单调队列可以优化?注意看,对于每个 $dp[i]$,我们实际上是要找它**往前数 $k$ 个 $dp$ 值中最小的那个**,(如果有同样小的,就是高度更高的),这就是区间求最小(滑动窗口)。
具体的:
```cpp
for(int i=1;i<n;i++){
while(q[r]>=dp[i]&&l<=r){
if(q[r]==dp[i]&&d[id[r]]>=d[i])
break ;
r--;
}
q[++r]=dp[i];
id[r]=i;
while(id[l]<=i-k) l++;
int t=q[l];
if(d[id[l]]<=d[i+1]) dp[i+1]=min(dp[i+1],t+1);
else dp[i+1]=min(dp[i+1],t);
}
```
### 斜率优化
例题:[P3195 [HNOI2008] 玩具装箱](https://www.luogu.com.cn/problem/P3195)
稍微有点复杂,(我理解来看)所以搬到
[P3195 [HNOI2008] 玩具装箱 & 斜率优化](https://www.luogu.com.cn/article/smusmp9r)