2025 年南京大学计算机学科体验专题营 游记
cjh20090318 · · 生活·游记
【博客园】。
前言
第一次夏令营,也许是,最后一次。
今天开始写,以前的事情视重要程度补充在里面。
正文
7.2?
在广东集训时看见了 Luogu Academic 群里有南京大学的同学转发夏令营的报名通知。
各类优秀的2026、2027届高中毕业学生,尤其是符合以下条件之一的:
- 获得信息学省级赛区(NOIP提高组),或NOI春季赛一等奖(针对部分NOIP未举办省份);
- 获得数学省级赛区(全国高中数学联赛)一等奖;
- 获得物理省级赛区(全国中学生物理竞赛)一等奖;
- 在以上两个不同比赛中均获得二等奖。
看下来只有年级是符合的哈哈哈。
没有一等奖,也没有两个学科的二等奖,所以把这事情放一边了没再理会。
8.6
上午乘坐飞机从广州白云国际机场,于下午到达南京禄口国际机场。
到达酒店时已经下午四点了,所以下午取消了原有的行程安排。
稍作休息后和时隔六年未见的小学同学共进晚餐,互相交流了一下当地的高考形式和政策。
众所周知的,江苏省统一采用新高考 I 卷,肯定是比重庆的新高考 II 卷难的,不过近几年也有在传重庆改用新高考 I 卷,总之压力上到我们这几届了哈,看谁先中奖。
不过话说回来,我难人难,我易人易,无论试卷难度如何改变,相对稳定不变的是大学在省份的录取位次。
| 学校 | 招生省份 | 录取批次 | 专业组/类别要求 | 2024最低分 | 2024最低位次 |
|---|---|---|---|---|---|
| 南京大学 | 重庆 | 本科批 | 物理类 | 677 | 447 |
| 南京大学 | 江苏 | 本科批(普通类) | 07组(物+不限) | 661 | 2296 |
| 南京大学 | 江苏 | 本科批(普通类) | 09组(物+化) | 663 | 1987 |
| 南京大学 | 江苏 | 本科批(普通类) | 08组(物+化) | 667 | 1405 |
| 南京大学 | 江苏 | 本科批(中外合作) | 11组(物+化) | 647 | 5643 |
| 东南大学 | 重庆 | 本科批 | 物理类 | 655 | 1941 |
| 东南大学 | 江苏 | 本科批(普通类) | 06组(物+化) | 660 | 2297 |
| 东南大学 | 江苏 | 本科批(普通类) | 07组(物+不限) | 656 | 3027 |
| 东南大学 | 江苏 | 本科批(普通类) | 08组(物+化) | 646 | 5644 |
以上是 Deepseek 整理的 2024 年公布的南京大学和东南大学在两省(市)物理类的录取情况。
可以发现在江苏省考这两所高校的难度是不相上下的,但在重庆市就是天差地别。
我爸也是第一次听说,毕竟他也没有研究过其他省份,所以和我同样惊讶。
革命尚未成功,同志仍须努力。
8.7
旅程细节就不在这里过多讲述了,想了解的可以去看我的 QQ 空间,这里挑一些重点讲。
下午参观南京大学(鼓楼校区),从南苑骑到北苑。
在某个时刻听我爸说我的报名审核通过了,第一反应还是有些激动,二等奖也能破格,第二反应是清华冬令营都要我说明我还是有点水平(不是。
在校园里四处骑车,参观了校史馆,里面有很多耳熟能详的科学家个人介绍,说明南京大学还是有深厚的底蕴。
逛南京大学文创店,一眼就被桌面立牌萌化了,一只小猫在船上“划水中”真的好可爱。
但是贫穷限制了我的想象力,所以除了上面这个还买了个南京大学文件袋就离开了。
8.11
看不懂但是大受震撼。
但是感觉确实挺真的。
8.13
自己花心思出了很久的题被高水平选手喷“根本不是题”。
还是有点伤自尊的,难过了很久。
8.14
达成成就课题模式金 48。
选曲仅供参考 Retribution IN16.2 98.2w,祈神 IN16.4 98.4w,时停 IN16.0 98.4w。
8.15
晚上挑战 @Whiking 进行别样的乒乓球大战,取得了 4:1 大胜!
8.16
在音游圈吃瓜,看到了如下名言:
我打音游好学校好你们就认为我是个好人了吗?
8.17
如此,年老。
8.18
考试,NOI plus!!!我不好说什么,反正没有三位数 /hanx。
惊奇发现两年前写的文章 化学方程式 突破了 100 赞,决定进行大更新。
成为了所谓的网红以后就是不一样,把这个古早作品翻出来又引起了一波流量。
8.19
因为 tad_ao 出差了,所以高 2028 届的同学被迫移动到了初 2026 届同学的机房,他们表示“没有一点人与人之间的信任”。
我觉得他们也对不起老师的信任吧。
他们吐槽机房木凳很硬没有靠背,我叫他们去尝试和老师协商换座椅,作为一个有基本人情的老师肯定都会同意的。
先做了一个神奇测试,测抑郁程度的,莫名其妙被诊断为轻度抑郁,我自己都不信。
接着完成了另一个神奇小测试你还会单身多久,结果是……
一年后的我,已经高三了,看来还是要专注于学习呢。
但愿好饭不怕晚。
拿到了 @cyh20100812 的化学作业,在少量她已经完成题目中惊奇的发现了
元素是守恒的,电子是凭空消失的。
写了一天的化学作业,非常好作业让我死去的必修一知识突然开始旋转,在下午完工了。
2025 年暑假 高 2028 届化学作业参考答案,密码可以直接私信我获取,50 只是开玩笑……
晚自习被教练拉到隔壁去谈话,才发现我是我们学校代表队水平最低的人。
还没开始考就给自己上压力了吗。
回到家以后和一个才退役的学妹略微交流,我想我的行动已经足够证明自己了,但是又有什么作用呢。
现实既如此,也不必遗憾。
8.20
上午考试,分数还能看,排名一般般。
后桌 @XiaoShanYunPan 一直在发布一些低质言论显得自己非常强大,结果他说前三题都是入门级题目结果都挂了,笑死。
没有同桌就开始讨厌后桌了(流汗。
Lyrith -迷宮リリス- AT16.5 打出了 99.34% 的不错成绩,上位 b8,最难 4k 轻松全 P,轮指打 5 纵连轻松爆炸。
会打 16.5/16.7 的 4k/5k,但还是研究不明白 16.6 的那一堆牛鬼蛇神。
8.21
这周一晚上在南京的小学同学告诉我他来重庆了。
但是他 23 日回南京,只能说是很遗憾地完美错过了哈,都没有在重庆好好招待他。
《 双 氢 飞 起 来 》
网络流,从来没学懂,这次还是一样。
考场上肯定是,不会建模,就算是建模了也不会写求解网络流算法。
学习了网络流的进阶:有/无源汇上下界网络流,这东西还是太困难了。
写模板题写了一天,直接被潘总质问了(哭。
谴责教练 @tad1 不把多的雪糕送我一个,好坏的人(流泪。
中午录制了 400 粉福,下载链接,不建议打开声音,因为打开声音带来的任何后果本人概不负责。
8.22
前往重庆江北国际机场 T2 航站楼,自从 T3 修好后几乎没再去。
相比 T3 确实显得有点黯然失色了。
飞机由于航路调整延误了两个小时,所以喜提飞机餐,有点饿了餐食和饮料都要了双份的(不要脸。
下午就直接乘坐地铁去南京大学报道了。
北门进去直接就是软件学院,乘坐电梯上到 5 楼,签字后领到了营员证和刻了本次活动名字的咖啡杯!意外之喜了。
顺便试机,在试机赛中拿到了 200 分 12 名的好成绩,第三题是用来提交视频文件的 md5 码的。
酒店的卫生间和卧室中间的玻璃是透明的,这怎么洗。
回来问前台才知道厕所里有个雾化开关,长见识了。
随便复习了一点组合数学就睡觉了。
8.23
开营仪式,短暂的讲话,宣布开营后笔试开始。
群论题,题目描述记不得了,
G 是一个pq 阶群,有质数p,q(p < q) ,满足p \mid q-1 ,证明G 是循环群。(给了一个 S 开头定理的材料)两个偏序结构
(A,\le_A),(B,\le_B) ,如果存在映射f:A\rightarrow B ,对于所有a_1,a_2 \in A ,使得a_1 \le_A a_2 \Leftrightarrow f(a_1) \le_B f(a_2) ,则称他们“序相似”。求证:
A 是一个可数集合,\preccurlyeq 是A 的偏序关系,存在集合B \subseteq \mathbb{Q} \cap (0,1) ,使得(A,\preccurlyeq),(B \le) 序相似。有一个正整数集合
S ,求是否存在一个子集T 满足元素和为2025 。(这是一段 NP-Hard 问题,NP 问题,多项式时间规约的材料)
请问这个问题是否是 NP-Hard 问题,若是请给出证明,若不是请给出一个多项式时间内解决问题的算法。
操作 $A(u,v)$ 为 $a_u = a_u \operatorname{xor} a_v$,其中 $u \neq v$。 经过一系列连续的操作后,可以明确的知道哪些位置(操作后)是 $0$ 或 $1$,最多可以知道几个位置?
上面是回忆的题目,可能描述不太准确。
总之就是除了第三题一道题都不会做。
中午就在学校北门对面的第一泉酒家吃饭,还可以,旁边桌是广附的同学?
下午是机试。
排座位
- 第一个人可以选择任意一个座位落座。 - 后来的人选择离有人座位的最远的空座位落座,如果距离相同可以选择任意一个。 例如 $(2,4,1,3),(2,4,3,1)$ 是合法的落座序列,但是 $(2,1,3,4),(2,3,1,4)$ 不是。 落座序列不同即存在一个人的选择座位不同。 求有多少组不同的落座序列,答案对 $m$ 取模。 $1 \le n \le 10^5, 1 \le m \le 10^9$。 ## 黑暗中的舞者 有 $n$ 个人,第 $i$ 个人的坐标是 $(x_i,y_i)$。 你作为舞者要去叫醒这 $n$ 个人,在每个时刻你可以唤醒和你 $x$ 坐标相同或者 $y$ 坐标相同的人。 起点和中点可以自由选择,每个时刻你可以选择向四连通的相邻位置移动,形式化地,$(x_1,y_1),(x_2,y_2)$ 相邻当且仅当 $\vert x_1 - x_2 \vert + \vert y_1 - y_2 \vert = 1$。 求叫醒所有人需要多长时间(不包含起点时间)。 例如现在有 $3$ 个人的坐标分别在 $(1,1),(2,2),(3,3)$,你从 $(1,2)$ 出发可以叫醒第一个人和第二个人,移动到 $(1,3)$ 可以叫醒第三个人,总时间为 $1$。 $1 \le n \le 5\times 10^5, 1 \le x,y \le 10^9$。 ## 六边形 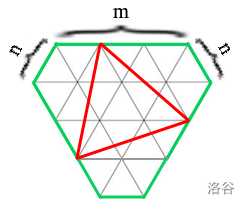 这是一个 $(m,n)$-六边形,内部由等边三角形组成的格点图。 你需要数出在其中端点在格点上,边不与内部的等边三角形重合(不是相交)的非退化等边三角形。 例如图中红色的三角形就是其中之一。 $1 \le n,m \le 10^{10}$。
上来简单观察了一下 A 合法序列,没有思路。
发现有人通过了 B,于是去看 B。
策略显然是走
所以对
大概半个小时把 B 写完了并通过了全部大样例,回去看 A。
第一个放置的位置在序列上对称方案数量相同,正确性显然。
对于所有空段一定是按中点分开,奇数段分成相同的两段,偶数段分为长度不同的两段。
对于一个长度为