洛谷月赛 LGR-117 选做
ix35
·
·
个人记录
今天上午并查集忘了写路径压缩了呀,不过做出来了个数数,但是这下还是真菜狗了!
然后就打算做做洛谷月赛,可惜很没感觉,只过了个 E,卡了一年常数才过,还是被暴打了!
赛后看了会 D(因为赛时看题面太长就没做!),也想出来了!
所以这里写写题解!
D 春分
题目大意:
过于复杂,点击链接。
---
### 题解:
这题很有 IOI 的感觉!不过比 IOI 还是难了一些!让我们逐步优化!
设左边液体的集合为 $L$,右边液体的集合为 $R$。
- 算法一:$M=\dfrac{2}{1}N$。
考虑给每种不同的液体都分配一块板,然后每次实验就找那两种液体对应的板放在中间即可!
- 算法二:$M=\dfrac{3}{2}N$。
$L$ 中每种液体分配一块板,$R$ 则拆分成大小相同的两部分 $R_1,R_2$,一开始只给 $R_1$ 中的液体分配一块板!
首先完成 $L\times R_1$ 的实验,然后将 $R_1$ 对应的板都翻转一下,将反面分配给 $R_2$ 使用,完成 $L\times R_2$ 的实验!
- 算法三:$M=\dfrac{5}{4}N$。
注意到一个事情,我们在右边使用一块正反面都有液体的板 $r$ 时,其实不一定会污染左边的板 $l$,只需要在中间隔上一块左边是干净的 $m$ 即可!
于是,我们可以优化上面的策略。$L$ 中每种液体分配一块板,$R$ 则拆分成大小相同的四部分 $R_1,R_2,R_3,R_4$,一开始只给 $R_1$ 中的液体分配一块板!
首先完成 $L\times R_1$ 的实验,然后把 $R_1$ 的板翻转后分给 $R_2$,再完成 $L\times R_2$ 的实验(注意这里采用中间隔板的方法,因此 $L$ 中的板的右侧不会被污染)!
然后将 $L$ 拆分为大小相同的 $L_1,L_2$,首先把 $L_1$ 的板翻转后分给 $R_3,R_4$,就完成了 $L_2\times (R_3+R_4)$ 的实验;再把 $L_2$ 的板翻转后分给 $L_1$,就完成了 $L_1\times (R_3+R_4)$ 的实验!
- 算法四:$M=\dfrac{7}{6}N$。
进行一定的精细分析即可从算法三进化到算法四,主要过程就是人脑搜索可行的解,下面直接给出构造:
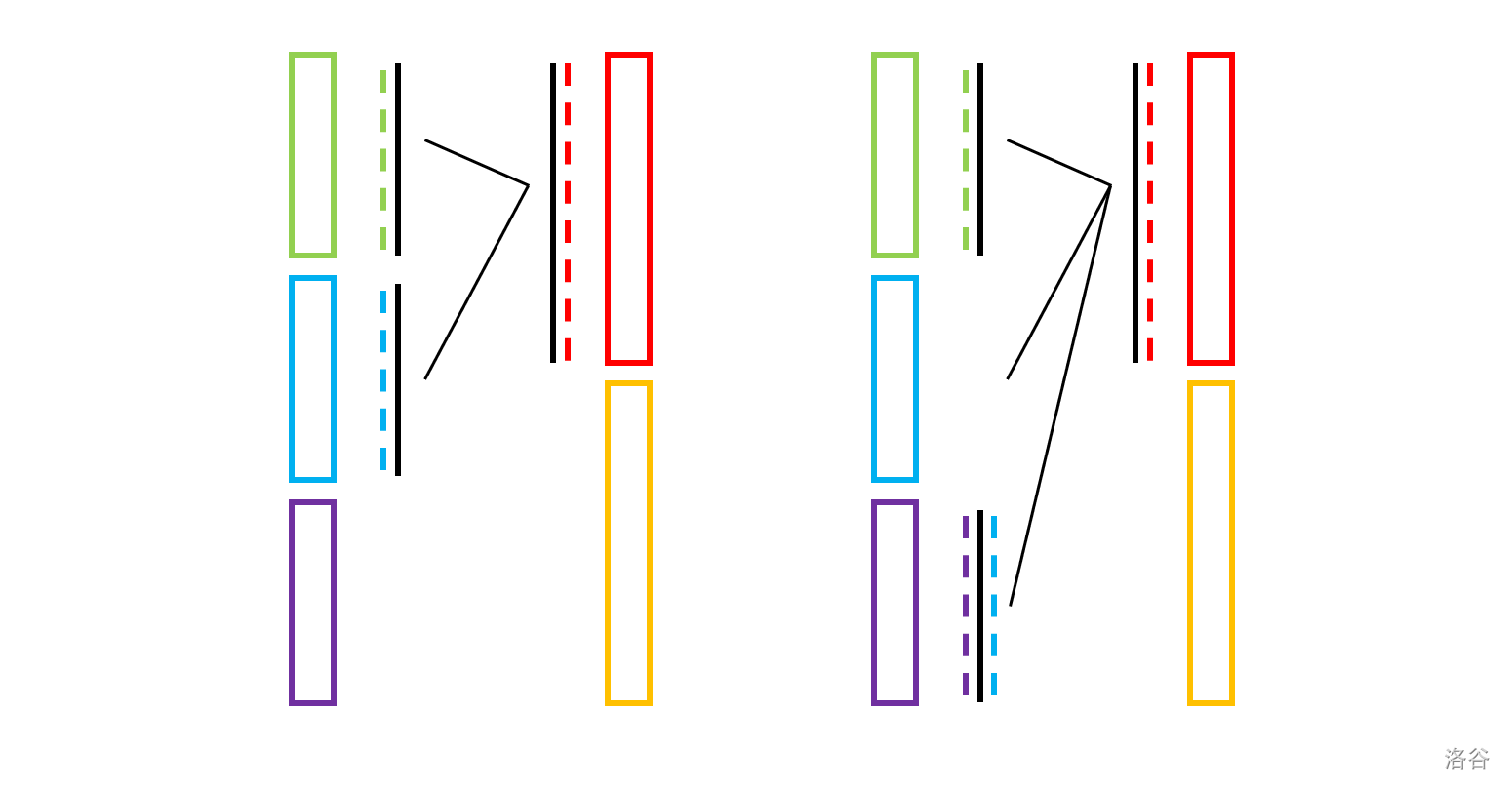
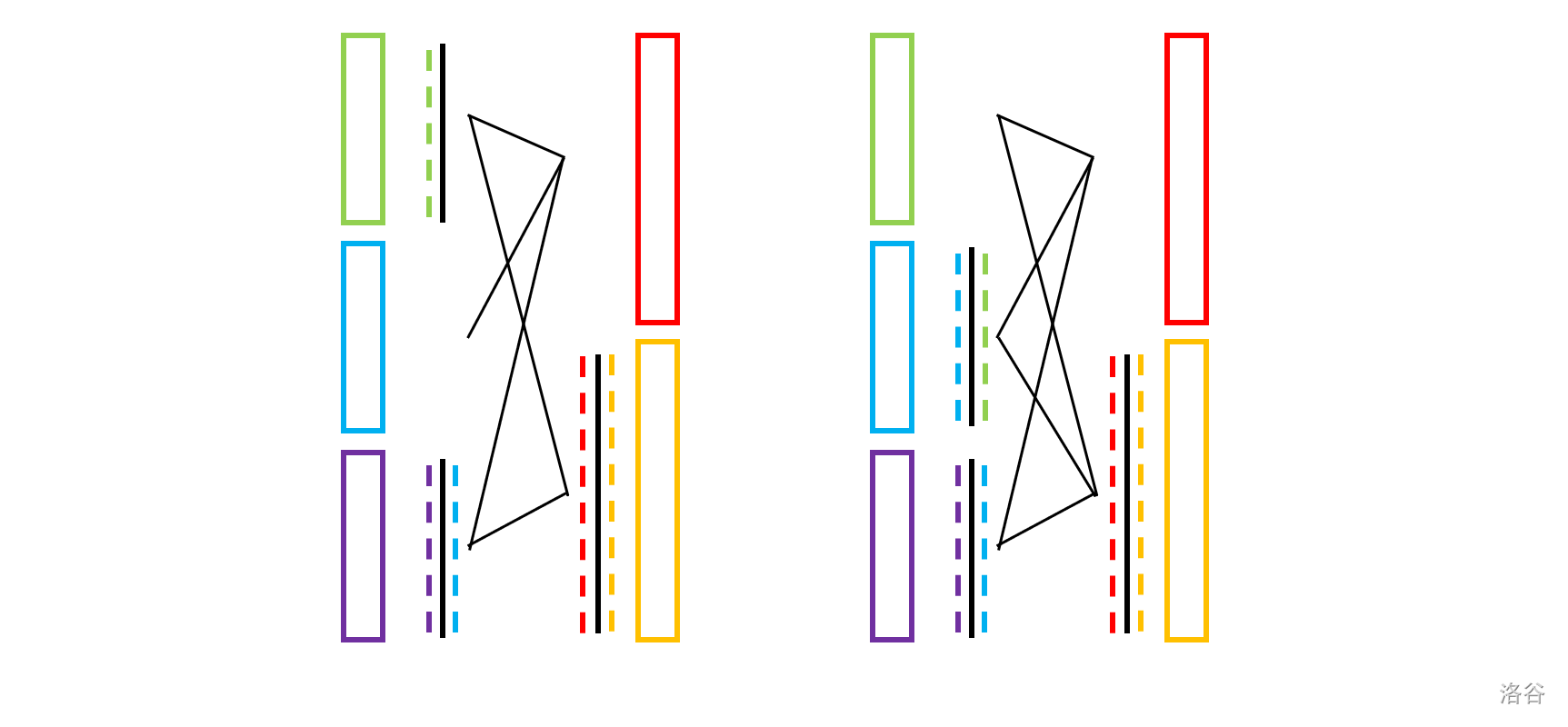
首先把 $L$ 三等分成 $L_1,L_2,L_3$(绿,蓝,紫),$R$ 二等分成 $R_1,R_2$(红,橙),一开始给 $L_1,L_2,R_1$ 分配隔板!
第一步:完成 $(L_1+L_2)\times R_1$ 的实验。
第二步:将 $L_2$ 的板子翻转后给 $L_3$,完成 $L_3\times R_1$ 的实验。
第三步:将 $R_1$ 的板子翻转后给 $R_2$,完成 $(L_1+L_3)\times R_2$ 的实验。
第四步:将 $L_1$ 的板子翻转后给 $L_2$,完成 $L_2\times R_2$ 的实验。
上图展示了全流程(左右分别为每种液体,黑色竖线表示隔板,两侧虚线表示那一侧沾上的液体,中间的细线表示已经完成的实验)!
---
## [E 清明](https://www.luogu.com.cn/problem/P8478)
### 题目大意:
给定 $a_1,\ldots,a_N$,对于每个 $a_i$,现在可以把 $a_i$ 分一部分给 $a_{i+1},a_{i+2},\ldots,a_{\min(N,i+k)}$,要求每一部分都是自然数。
设得到的序列为 $b_1,\ldots,b_N$,对 $\prod b_i$ 求和,对 $998244353$ 取模。
$N\leq 32$。
---
### 题解:
首先转化一下问题:
- 有一个 $N\times N$ 列的矩阵 $M$,第 $i$ 列的和为 $a_i$,并且 $M_{i,j}$ 只有 $0\leq i-j\leq k$ 时才可以是非零的(也就是一个下三角的带状矩阵),求每一行的和的乘积之和。
考虑拆贡献,也就是在每一行选择一个非零位置,然后求出这些位置乘积之和,然后再对所有方案求和!
首先做一个准备工作,设 $f(A,p,q)$ 表示将 $A$ 分为 $p+q$ 个自然数,前 $p$ 个自然数的乘积之和,这可以用一个组合数计算,对每个 $A=a_i,\ p,q\leq N$ 预处理这个结果!
然后可以开始状压 DP 了:设 $dp(i,S)$ 表示目前在前 $i$ 列选择了一些位置,并且选择的行的集合为 $S$,所有方案的选出位置乘积之和,那么显然有 $dp(i-1,S)\times f(a_i,\min(N-i+1,k+1),|T|)\to dp(i,S+T)$,表示在第 $i$ 列选择 $T$ 这个集合。
注意到在状态 $dp(i,S)$ 中一定有 $\{1,\ldots,i-1\}\subseteq S$,并且 $S\cup \{i+k+1,\ldots,N\}=\varnothing$,所以对于每个 $i$ 只有至多 $2^k$ 个合法状态!
于是这个 DP 如果暴力转移是 $O(N\times 3^k)$ 的,由于贡献只和 popcount 有关,所以可以优化到 $O(N^3\times 2^k)$。
我们发现,在上面的 DP 过程中,$\{1,\ldots,k+1\}$ 这些行是“不必区分”的,因为从第一列开始这些行就一直能被选,所以我们就有另一种 DP:设 $dp(i,j,S)$ 表示在前 $i$ 列选择一些位置,目前 $\{k+2,\ldots,N\}$ 这些行中被选择的为集合 $S$,并且 $\{i,i+1,\ldots,k+1\}$ 这些行中选择了 $j$ 行,这个 DP 状态数看似是 $O(N^2\times 2^{N-k})$,但实则是 $O(N\times 2^{N-k})$ 的,请读者自行思考!
暴力复杂度 $O(N\times 3^{N-k})$,这里同样贡献只和 popcount 有关,所以可以优化到 $O(N^3\times 2^{N-k})$。
平衡复杂度后,时间复杂度为 $O(N^3\times 2^{\frac{N}{2}})$,需要一定程度的卡常!