多项式学习笔记
Ptilopsis_w
·
·
个人记录
快速傅里叶变换(FFT)
问题来源
一切多项式算法的基础都是快速得到两个多项式的乘积,但是暴力求乘积是 O(n^2) 的。
我们观察时间复杂度到底大在哪:
\sum _{i=0} ^{n-1}
\sum _{j=0} ^{m-1}
a_ix^i * b_jx^j
问题就在于我们每个 i 都要枚举一边 j,而且每次贡献产生的位置还不一样,无法优化。
我们还知道如果是点值表示的多项式的话,直接对应点值相乘即可 O(n) 做到多项式乘法。
所以我们可以考虑先把多项式转化成点值,乘完再转化回来。
求点值的话就是将 x = 0,1,\cdots,n-1 分别代入
f(x) = a_0 + a_1x^1 + \cdots + a_{n-1}x^{n-1}
但是这个式子也存在贡献 x^1,x^2,x^3 在代入不同 x 时不重复的问题,最主要原因还是实数域是无穷大的,根本没法造成重复贡献,所以时间复杂度还是 O(n^2) 的。
解决办法
实数域没法优化,如果我们抛弃实数域呢?如果能找到一个 x^0,x^1,\cdots,x^{n-1} 会发生重复的东西,问题就可以解决了。
自乘会循环的东西,我们应该容易想到旋转和取模,而这正对应了在虚数域使用单位根的 FFT 和在同余系使用原根的 NTT 两种算法。
这里就不列举单位根和原根的性质了。
先说在虚数域使用单位根的 FFT 算法,我们知道旋转操作转任意整数圈后的状态是和原来一样的,而我们又需要一种支持四则运算且自乘对应旋转的东西,而这个东西就可以是虚数域中的单位根。
我们知道虚数有三角表示,而两个虚数相乘就是模长相乘幅角相加,如果两个虚数模长都是 1 的话就只剩下幅角相加了,而幅角相加整好就是我们需要的旋转操作。
我们把单位根的 0 \sim n-1 次方代入,也可以确定这个多项式。
具体做法
因为只有发生旋转(自乘)才能产生重复贡献,所以我们将 A(x) 这个多项式写成 A(x)=A_1(x^2)+xA_2(x^2) 的形式,这个可以将 A(x) 对下标奇偶性分类构造出来,即
A_1(x) = a_0 + a_2x + a_4x^2 + \cdots + a_{n-2}x^{\frac{n}{2}-1} \\
A_2(x) = a_1 + a_3x + a_5x^2 + \cdots + a_{n-1}x^{\frac{n}{2}-1} \\
这样就可以构造出来 A(x) = A_1(x^2) + xA_2(x^2),构造 x^2 的原因是因为需要利用旋转。
然后考虑 (w_n^k)^2,因为转一圈是不变的,所以 (\omega_n^k)^2 = (\omega_n^{k+\frac{n}{2}})^2,且有 \omega_n^k = -\omega_n^{k+\frac{n}{2}}(转半圈),所以我们分别将 \omega_n^k 和 \omega_n^{k+\frac{n}{2}} 代入得
A(\omega_n^k) & = A_1(\omega_n^{2k}) + \omega_n^kA_2(\omega_n^{2k}) \\
A(\omega_n^{k+\frac{n}{2}}) & = A_1(\omega_n^{2k+n}) + w_n^{k+\frac{n}{2}}A_2(\omega_n^{2k_n})
\end{aligned}
用 \omega_n^k 替换掉 \omega_n^{k+\frac{n}{2}} 得
A(\omega_n^k) & = A_1(\omega_n^{2k}) + \omega_n^kA_2(\omega_n^{2k}) \\
A(\omega_n^{k+\frac{n}{2}}) & = A_1(\omega_n^{2k}) - w_n^{k}A_2(\omega_n^{2k})
\end{aligned}
现在我们成功利用了单位根的旋转性质使得求出 A(\omega_n^k) 后即可 O(1) 求出 A(\omega_n^{k+\frac{n}{2}})。
现在的问题就是分别求出 A_1(x) 和 A_2(x) 在 \omega_{\frac{n}{2}}^0, \omega_{\frac{n}{2}}^1, \cdots, \omega_{\frac{n}{2}}^{\frac{n}{2}-1} 处的点值,我们发现问题规模缩小到了 \frac{1}{2},递归下去求解即可做到 O(n \log n) 将系数表示的多项式转化为点值表示的多项式。
剩下的问题就是如何转化回去,我们直接用 \omega_n^{-k} 代替 \omega_n^k 逆操作回去,然后每一项的系数除以 n 即可(证明还是推式子)。
最后一个问题是这个算法要求 n 必须是 2 的整次幂,我们将多项式扩展为第一个 \ge n 的 2 的整次幂即可,多出来的项系数直接设成 0。
优化常数
如果直接用递归写法的话,常数会非常大,我们更常用的是非递归写法:
考虑 x^i 的系数 a_i 最终的下标会变到哪个位置。
在每次的递归中, a_i 会因为不同的奇偶性有不同的去向:
i \longrightarrow
\begin{cases}
i/2, i \mid 2 \\
n/2+i/2, i \nmid 2
\end{cases}
因为 n 一定是 2 的整次幂,而且除数还是 2, 我们考虑将其转化为位运算表示: (设 n=2^b)
i \longrightarrow
\begin{cases}
i>>1,(i\&1)=0 \\
(1<<(b-1)) \, | \, (i>>1) , (i\&1)=1
\end{cases}
这个操作我们可以看做每个下标最高位是 b-1,每递归一层, a_i 就会跑到 将 i 的最低位移到最高位 那个位置上,所以递归到最后 a_i 所在位置就是将 i 的二进制序列翻转后的位置上,所以我们可以递推求出每个位置二进制翻转后到达的位置,直接交换这两个数即可(成对的)。
代码实现
typedef complex<double> poly;
void init(int n)
{
lim = 1, bit = 0;
while(lim <= n) // 将 n 扩大为 2 的整次幂
lim <<= 1, bit++;
for(int i = 1; i < lim; i++) // r[i] 为 i 二进制序列翻转后所在位置
r[i] = (r[i>>1]>>1) | ((i&1)<<(bit-1));
}
void dft(poly *a)
{
for(int i = 0; i < lim; i++) // 先把每个数放到它最终的位置上
if(i < r[i]) swap(a[i], a[r[i]]);
for(int mid = 1; mid < lim; mid <<= 1) // 模拟递归过程,从最底层开始
{
poly wn(cos(PI/mid), sin(PI/mid)); // 单位根
for(int j = 0, k = 0; j < lim; j += (mid<<1), k = j) // 套式子
for(poly w = 1; k < j+mid; k++, w *= wn)
{
poly x = a[k], y = w*a[k+mid];
a[k] = x+y, a[k+mid] = x-y;
}
}
}
void idft(poly *a)
{
for(int i = 0; i < lim; i++)
if(i < r[i]) swap(a[i], a[r[i]]);
for(int mid = 1; mid < lim; mid <<= 1)
{
poly wn(cos(PI/mid), -sin(PI/mid)); // 取反方向的单位根
for(int j = 0, k = 0; j < lim; j += (mid<<1), k = j)
for(poly w = 1; k < j+mid; k++, w *= wn)
{
poly x = a[k], y = w*a[k+mid];
a[k] = x+y, a[k+mid] = x-y;
}
}
// 跟 dft 一样,就是需要多除一个 lim
for(int i = 0; i < lim; i++)
a[i] /= lim;
}
快速数论变换(NTT)
我们发现在同余系下原根也具有类似的性质,所以直接用原根替代单位根,再加上取模就可以了。
FFT 常数小,精度高,但是只支持系数值域较小时的情况。
NTT 常数大,但是可以支持系数非常大的情况(比如数数题中需要取模的情况)。
有了速度很快的多项式乘法,我们就可以进行多项式的许多操作了。
多项式求逆
对于一个多项式 A(X),求出一个多项式 A^{-1}(x) 使得 A(x)A^{-1}(x) \equiv 1 \pmod{x^n}。
我们考虑递归求解,设我们已经解出了 B(x) \equiv A(x) \pmod{x^{\lceil \frac{n}{2} \rceil}},我们用 B(x) 推出 A^{-1}(x)。
因为我们要从 \bmod \space x^{\lceil \frac{n}{2} \rceil} 推到 \bmod \space x^n,所以肯定需要平方操作,但是直接平方会造成 B(x) 与 A^{-1}(x) 不相等,我们进行一个移项操作
B(x)
& \equiv
A^{-1}(x)
& \pmod{x^{\lceil \frac{n}{2} \rceil}} \\
B(x) - A^{-1}(x)
& \equiv
0
& \pmod{x^{\lceil \frac{n}{2} \rceil}} \\
[ B(x) - A^{-1}(x)]^2
& \equiv
0
& \pmod{x^n} \\
B(x)^2 - 2B(x)A^{-1}(x) + A^{-1}(x)^2
& \equiv
0
& \pmod{x^n}
\end{aligned}
两边同时乘上 F(x) 得
B(x)^2F(x) - 2B(x) + A^{-1}(x)
\equiv
0
& \pmod{x^n} \\
A^{-1}(x)
\equiv
2B(x) - B(x)^2F(x)
& \pmod{x^n}
\end{aligned}
然后我们可以递归+多项式乘法求出一个多项式的逆元。
多项式开根(sqrt)
运用和求逆同样的思想。
设已经求出来了 B^2(x) \equiv A(x) \pmod{\lceil \frac{n}{2} \rceil},通过 B(x) 求出 F^2(x) \equiv A(x) \pmod{x^n}。
B(x)
& \equiv
F(x)
& \pmod{x^{\lceil \frac{n}{2} \rceil}} \\
B(x) - F(x)
& \equiv
0
& \pmod{x^{\lceil \frac{n}{2} \rceil}} \\
(B(x)-F(x))^2
& \equiv
0
& \pmod{x^n} \\
B^2(x) - 2B(x)F(x) + F^2(x)
& \equiv
0
& \pmod{x^n} \\
B^2(x) - 2B(x)F(x) + A(x)
& \equiv
0
& \pmod{x^n} \\
F(x)
& \equiv
\frac {A(x) + B^2(x)} {2B(x)}
& \pmod{x^n} \\
\end{aligned}
然后就可以用多项式求逆解决了。
多项式对数函数(ln)
求 B(x) = ln(A(x))。
$$
B'(x) = \frac{A'(x)}{A(x)}
$$
然后用多项式求逆可以求出 $B'(x)$,然后再不定积分回去就是 $B(x)$。
## 多项式指数函数(exp)
### 牛顿迭代
求多项式 $\exp$ 首先我们需要先了解牛顿迭代。
牛顿迭代是用来快速求函数 $f(x)$ 的近似零点的。
假设我们已经求得了一个近似值 $x_0$,那么我们过 $(x_0, f(x_0))$ 作 $f(x)$ 的切线,取切线与 $x$ 轴的交点作为新的 $x_0$。
用一张洛谷题解的图:
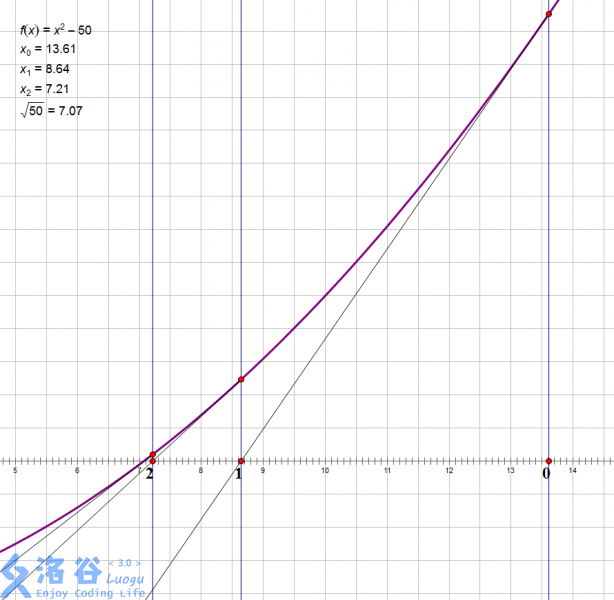
我们直接用点斜式写出切线方程:
$$
y-f(x_0) = f'(x_0)(x-x_0)
$$
当 $y = 0$ 时,有
$$
x = x_0 - \frac{f(x_0)}{f'(x_0)}
$$
### 解法
牛顿迭代的式子也可以直接放到多项式上来用。
我们需要求 $B(x) \equiv e^{A(x)} \pmod{x^n}$。
两边同时取 $\ln$ 得
$$ \begin{aligned}
\ln(B(x))
& \equiv
A(x)
& \pmod{x^n} \\
\ln(B(x)) - A(x)
& \equiv
0
& \pmod{x^n} \\
\end{aligned} $$
我们设 $G(B(x)) = \ln(B(x)) - A(x)$。
我们的目的就是求出一个 $B(x)$ 使得 $G(B(x)) = 0$,也就是将 $B(x)$ 看做自变量求 $G(B(x))$ 的零点。
套入牛顿迭代公式得
$$ \begin{aligned}
B(x)
& =
B_0(x) - [\ln(B_0(x))-A(x)] \cdot B_0(x) \\
B(x)
& =
B_0(x) \cdot (1 - \ln(B_0(x))+A(x))
\end{aligned} $$
这样不断迭代即可求得 $B(x)$。
本质上每迭代一次精度是翻倍的,也就是用 $B_0(x) \equiv e^{A(x)} \pmod{x^{\lceil \frac{n}{2} \rceil}}$,迭代一次可以得到 $B(x) \equiv e^{A(x)} \pmod{x^n}$。
然后就是经典的递归做法了。
## 多项式除法
给定 $n$ 次多项式 $F(x)$ 和 $m$ 次多项式 $G(x)$,求出一个 $n-m$ 次多项式 $A(x)$ 和 一个小于 $m$ 次的多项式 $B(x)$ 满足 $F(x)=A(x)G(x) + B(x)$。
将 $\frac{1}{x}$ 代入关系式
$$ \begin{aligned}
F(\frac{1}{x})
& =
A(\frac{1}{x})G(\frac{1}{x}) + B(\frac{1}{x}) \\
x^nF(\frac{1}{x})
& =
A(\frac{1}{x})G(\frac{1}{x}) + x^nB(\frac{1}{x}) \\
x^nF(\frac{1}{x})
& =
x^{n-m}A(x) \cdot x^mG(x) + x^{n-m+1}\cdot x^{m-1}B(x)
\end{aligned} $$
发现 $x^nF(\frac{1}{x})$ 就是将 $F(x)$ 的系数前后翻转一下,设其为 $F_R(x)
F_R(x)
\equiv
A_R(x)G_R(x) + x^{n-m+1} B_R(x)
因为 A_R(x) 是 n-m 次多项式,所以两边同时 \bmod \space x^{n-m+1} 对结果无影响,取模后 B_R(x) 就没了。
F_R(x)
& \equiv
A_R(x)G_R(x)
& \pmod{x^{n-m+1}} \\
A_R(x)
& \equiv
\frac{F_R(x)}{G_R(x)}
& \pmod{x^{n-m+1}}
\end{aligned}
用多项式求逆即可求出 A(x),然后
B(x)
=
F(x) - A(x)G(x)
这样 B(x) 也求出来了。
多项式多点求值
设需要求值的多项式为 F(x),需要求的点值为 F(x_1), F(x_2), \cdots, F(x_m)。
默认你会了多项式除法,那么有 F(x_0) = F(x) \bmod (x-x_0)。
证明:
F(x)
& =
\sum_{i=0}^{n} a_ix^i \\
F(x)
& =
\sum_{i=0}^{n} a_i(x-x_0+x_0)^i \\
F(x)
& =
\sum_{i=0}^{n} a_i
\sum_{j=0}^{i}
C_i^j(x-x_0)^jx_0^{i-j}
\end{aligned}
只有在 j=0 时 C_i^j(x-x_0)^jx_0^{i-j} 才能在 F(x) \bmod (x-x_0) 中留下来,所以得到
F(x) \bmod (x-x_0) = \sum_{i=0}^{n} a_ix_0^i = F(x_0)
但是如果直接做 m 次多项式除法时间复杂度是 O(mn \log n) 的,考虑优化。
首先有个很显然的性质: 若 a|b,则 x \bmod a = (x \bmod b) \bmod a。
所以我们可以考虑一手分治,设 G_{l,r}(x) = \prod\limits _{i=l}^{r} (x-x_i),设 F_{l,r}(x) = F(x) \bmod G_{l,r}(x) 我们每次取当前区间 [l,r] 的 mid,然后求出 F_{l,r}(x) \bmod G_{l,mid}(x) 并递归进入 [l,mid] 区间,[mid+1,r] 区间同理,这样递归到 l=r 时即可解出这个位置的点值。
具体实现可以类似建线段树一样先预处理出所有要用到的 G_{l,r}(x),然后再分治递归下去。
时间复杂度 O(n \log^2 n)。
多项式快速插值
首先我们有 O(n^2) 的拉格朗日插值的式子:
F(x)
=
\sum _{i=1}^n
y_i
\prod _{j \not = i}
\frac{x-x_j}{x_i-x_j}
那个 j \not= i 的限制很烦人,考虑上下同时乘一个 (x_i-x_i),得
F(x)
=
\sum _{i=1}^n
y_i
\frac
{(x_i-x_i)\prod _{j\not=i}(x-x_j)}
{\prod _{j} (x_i-x_j)}
此时我们将 \prod _{j} (x-x_j) 看成一个多项式 G(x),那么分母就是 G(x_i),式子就变成了
F(x)
=
\sum _{i=1} ^{n}
y_i
\frac{(x_i-x_i)}{G(x_i)}
\prod _{j \not= i}
(x-x_j)
其中 (x_i-x_i) = 0, G(x_i) = 0,分式不能直接计算,但是 \lim\limits _{x \rightarrow x_i} \frac{x-x_i}{G(x_i)} 可以用洛必达法则计算,即
\lim _{x \rightarrow x_i} \frac{x-x_i}{G(x_i)}
=
\frac{1}{G'(x_i)}
代入式子中得
F(x) = \sum _{i=1}^n \frac{y_i}{G'(x_i)} \prod _{j \not= i}(x-x_j)
其中 G'(x_i) 可以用多项式多点求值解决,后面的 \prod\limits _{j \not= i}(x-x_j) 可以在多点求值的分治过程中一块用分治解决,时间复杂度 O(n \log^2 n)。
多项式复合函数
给定 F(x),G(x),求 H(x) \equiv F(G(x)) \pmod{x^{n+1}}。
所求的式子即是
F(G(x)) = \sum _{i=0}^n [x^i] F(x)G(x)^i
但是 G(x)^i 不能全算出来也没法全部预处理,但是我们可以预处理一部分。
考虑像分段打表一样,将 i 以根号为界拆分,设 L = \sqrt{n}, i=aL+b,则
&\sum _{i=0}^n
[x^i] F(x)G(x)^i
\\
& =
\sum _{a=0}^{L-1}
\sum _{b=0}^{L-1}
[x^{aL+b}] F(x) G(x)^{aL+b}
\\
& =
\sum _{a=0}^{L-1}
G(x)^{aL}
\sum _{b=0}^{L-1}
[x^{aL+b}] F(x) G(x)^b
\end{aligned}
其中 G(x)^{aL},G(x)^b 可以 NTT 预处理,然后后面的部分直接枚举然后暴力计算,时间复杂度 O(n^2 + n \log n \sqrt n)。
实际上 O(n^2) 部分常数非常小完全能过,但是 NTT 部分常数大需要写的好看。