关于函数的“干货”
tiancai_1234
·
·
个人记录
说在前面的话
内容虽然比较基础,然而基础的东西不一定简单,且基础的东西必然重要。
本期内容有点长,建议配上薯条
ok,开讲!
$\quad$ 函数的定义中,对每个元素 $x \in D$,按对应法则 $f$,总有唯一确定的值 $y$与之对应,这个值称为函数 $f$ 在 $x$ 处的**函数值**,记作 $f(x)$,即 $y=f(x)$。因变量 $y$ 与自变量 $x$ 之间的这种依赖关系,我们通常称为**函数关系**。函数值 $f(x)$ 的全体所构成的集合称为函数 $f$ 的**值域**,记作 $R_f$ 或 $f(D)$,即
$$R_f = f(D) = \left\{y|y=f(x),x \in D\right\}.$$
$\quad$ 需要指出,按照上述定义,记号 $f$ 和 $f(x)$ 的含义是有区别的:前者表示自变量 $x$ 和因变量 $y$ 之间的对应法则,而后者则表示与自变量 $x$ 对应的函数值。但为了叙述方便,习惯用上常用记号"$f(x),x \in D$"或"$f=f(x),x \in D$"来表示定义在 $D$ 中的函数,这时应理解为由它所确定的函数 $f$。
$\quad$ 表示函数的记号是可以任意选取的,除了常用的 $f$ 外,还可以用其他的英文字母或者希腊字母,如 $g,F,\varphi$ 等。相应的,函数可记作 $y=g(x),y=F(x),y=\varphi(x)$ 等。有时还直接用因变量的记号来表示函数,即把函数记作 $y=y(x)$。但在同一个问题中,讨论到几个不同的函数时,为了表示区别,需用不同的记号来表示它们。
$\quad$ 函数是从实数集到实数集的映射,其值域总在 $R$ 以内,因此构成函数的要素是:定义域 $D_f$ 及对应法则 $f$(这里高中都讲过,我就不多说)。如果两个函数的定义域相同,对应法则也相同,那么这两个函数就是相同的,否则就是不同的。
$\quad$ 函数的定义域通常按以下两种情形来确定:一种是对有实际背景的函数,根据实际背景中变量的实际意义确定。例如,在自由落体运动中设物体下落的时间为 $t$ ,下落的距离为 $s$ ,开始下落的时刻 $t=0$,落地的时刻 $t=T$,则 $s$ 和 $t$ 之间的函数关系是
$$s=\dfrac{1}{2}gt^2,t\in[0,T].$$
这个函数的定义域就是区间 $[0,T]$;另一种是抽象地用解析式表达的函数,通常约定这种函数的定义域是使得解析式有意义的一切实数组成的集合,这种定义域称为函数的**自然定义域**。在这种约定下,一般的用解析式表达的函数可用"$y=f(x)$"表示,而不必再表出 $D_f$。例如函数 $y=\sqrt{1-x^2}$ 的定义域是闭区间 $[-1,1]$,函数 $y=\dfrac{1}{\sqrt{1-x^2}}$ 的定义域是开区间 $(-1,1)$。
$\quad$ 表示函数的主要方式有三种:表格法,图形法,解析法(也叫做公式法),这在中学里大家想必都已经熟悉。其中,用图形法表示函数是基于函数图形的概念,即坐标平面上的点集
$${ P (x,y)|y = f(x),x \in D}$$
称为函数 $y = f(x),x\in D$ 的**图形**,如下图(目前不知道怎么画曲线,请见谅)。图中的 $R_f$ 表示函数 $y=f(x)$ 的值域。
下面举几个函数的例子
1. $y=2$ 的定义域 $D=(-\infty,+\infty)$,值域 $W=\{2\}$,它的图形是一条平行于 $x$ 轴的直线,如下图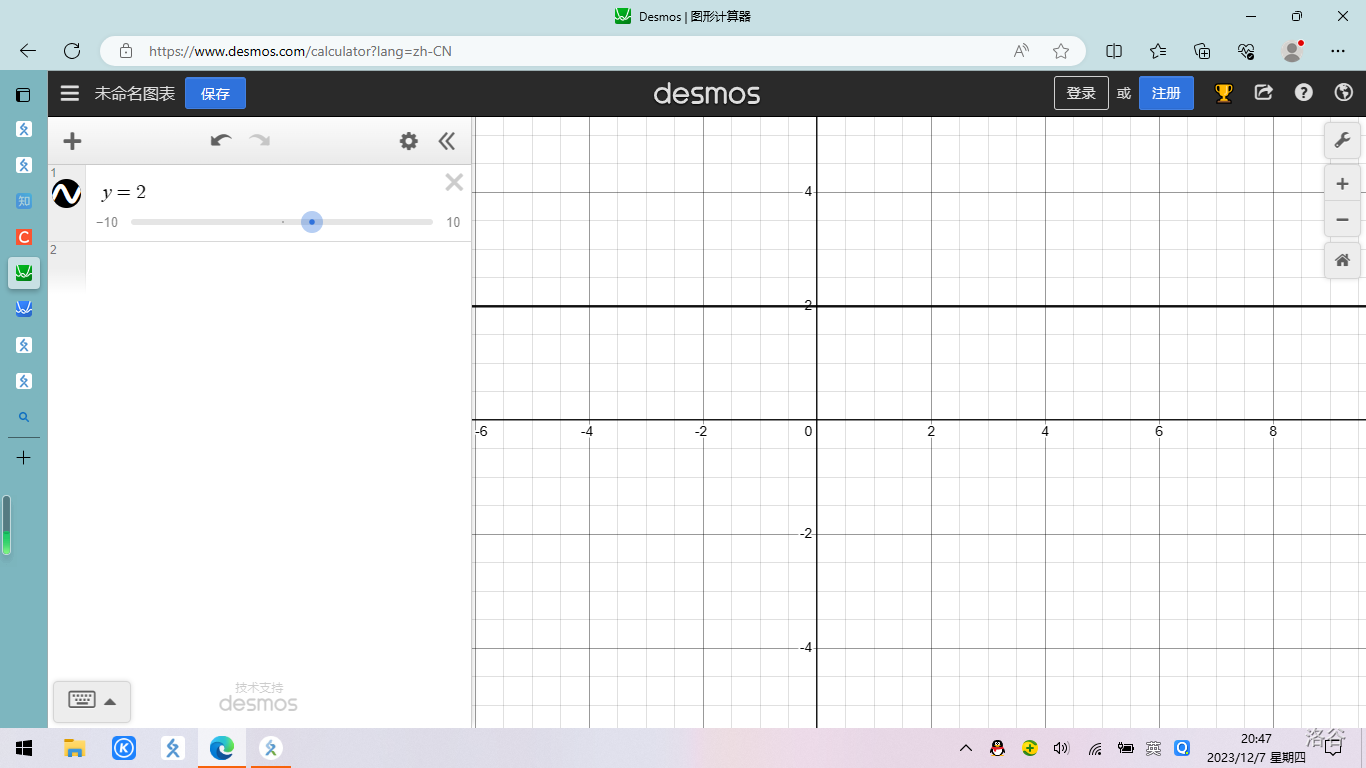
2. 函数
$$y=|x|=\begin{cases}-x&x<0\\x&x\geqslant0\end{cases}$$
的定义域 $D=(-\infty,+\infty)$,值域 $R_f=[0,+\infty)$,它的图形如下图所示,这个函数被称为**绝对值函数**
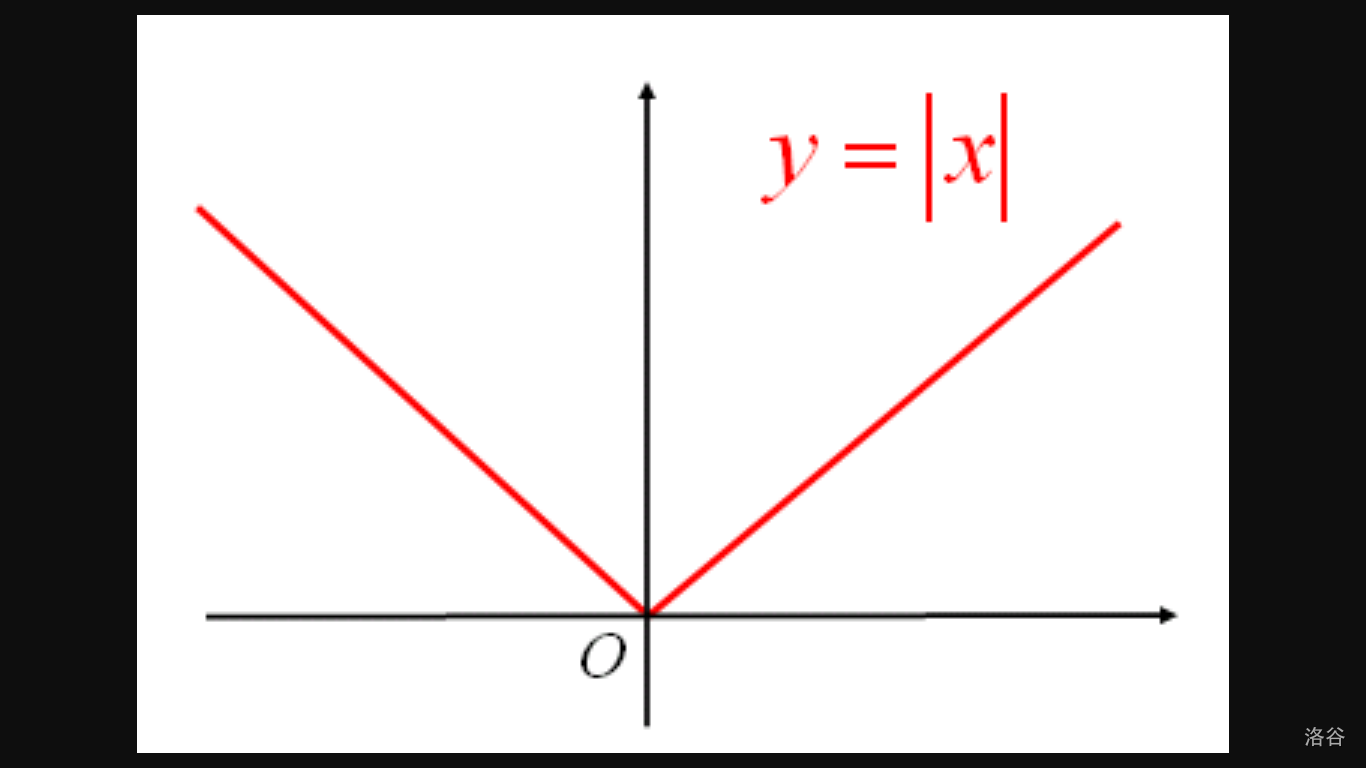
3. 函数
$$y=sgn x=\begin{cases}-x&x<0\\0&x=0\\1&x>0\end{cases}$$
称为**符号函数**,它的定义域 $D=(-\infty,+\infty)$,值域 $R_f=\{-1,0,1\}$,它的图形如下图所示,。对于任何实数 $x$,下列关系成立
$$x=sgn\;x\cdot|x|.$$
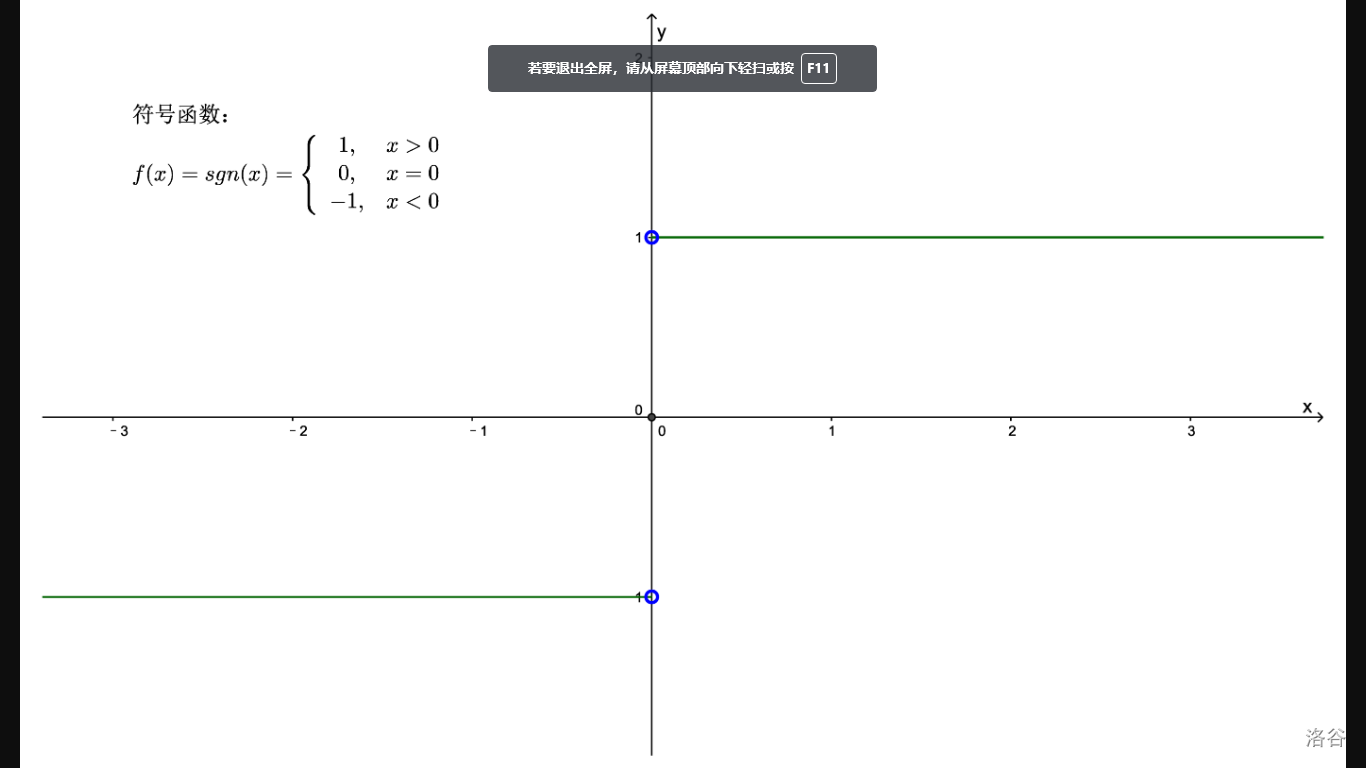
例8. 设 $x$ 为任一实数,不超过 $x$ 的最大整数称为 $x$ 的**整数部分**,记作 $[x]$。例如,$\left[\dfrac{5}{7}\right] =0$,$[\sqrt{2}]=1$,$[\pi]=3$,$[-1]=-1,[-3.5]=-4$(感觉和c++中的abs函数没什么不一样)。把 $x$ 看作变量,则函数
$$y=[x]$$
的定义域 $D=(-\infty,+\infty)$,值域 $R_f=Z$。它的图形如下图所示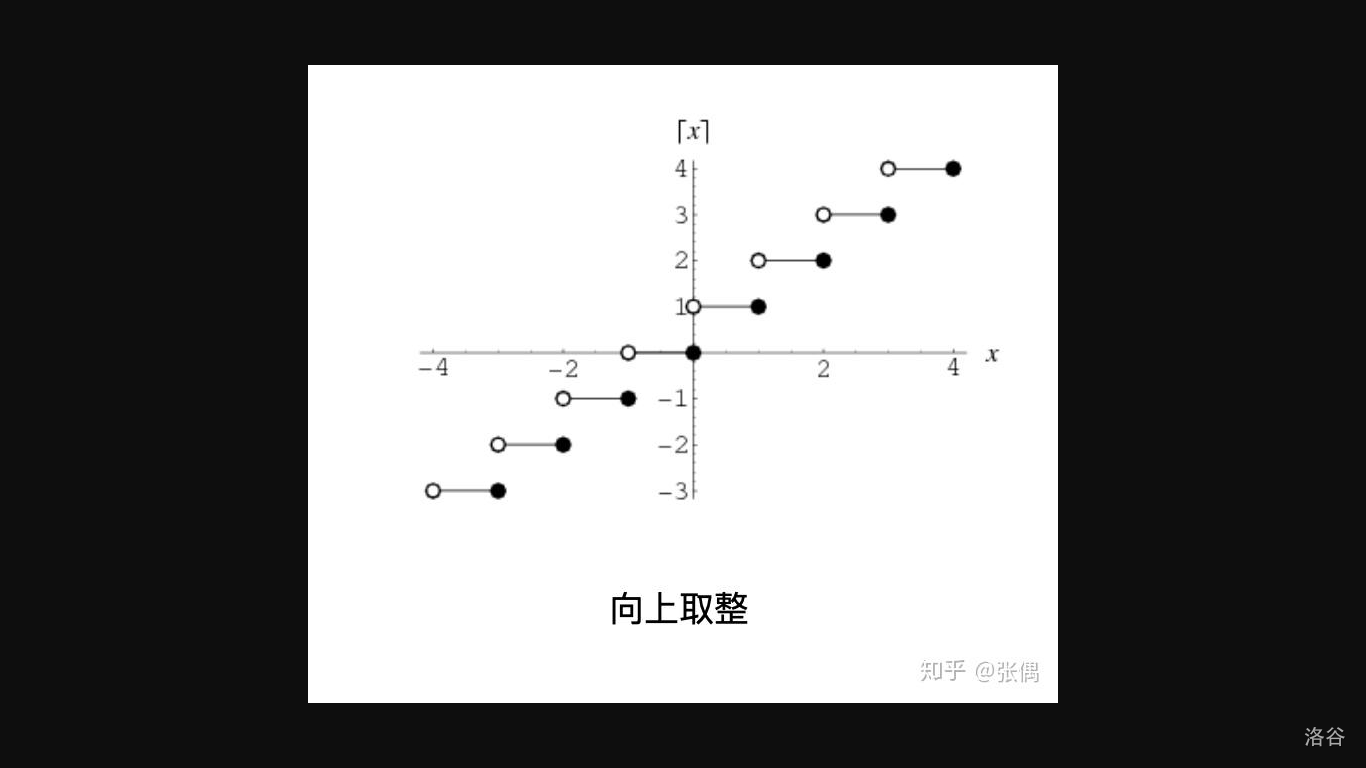这个图形称为**阶梯曲线**。在 $x$ 为整数值处,图形发生跳跃,跃度为 $1$。这个函数称为**取整函数**。在例1和例2中看到,有时一个函数要用几个式子表示。这种在自变量的不同变化范围中,对应法则用不同式子来表达的函数,通常我们称之为**分段函数**。
例9. 函数
$$y=f(x)=\begin{cases}\sqrt[2]{x}&0\leqslant x\leqslant1\\1+x&x>1\end{cases}$$
是一个分段函数。它的定义域 $D=[0,+\infty)$。当 $x\in[0,1]$ 时,对应的函数表达式 $f(x)=\sqrt[2]x$;当 $x\in(1,+\infty)$ 时,对应的函数表达式 $f(x)=1+x$。例如,$\frac{1}{2}\in[0,1]$,所以 $f\left(\dfrac{1}{2}\right)=2\quad\sqrt{\frac{1}{2}}=\sqrt{2}$;所以 $f(1)=2 \sqrt{1}=2$;$3\in(1,+\infty)$,所以 $f(3)=1+3=4$。这个函数的图形大概如下图所示
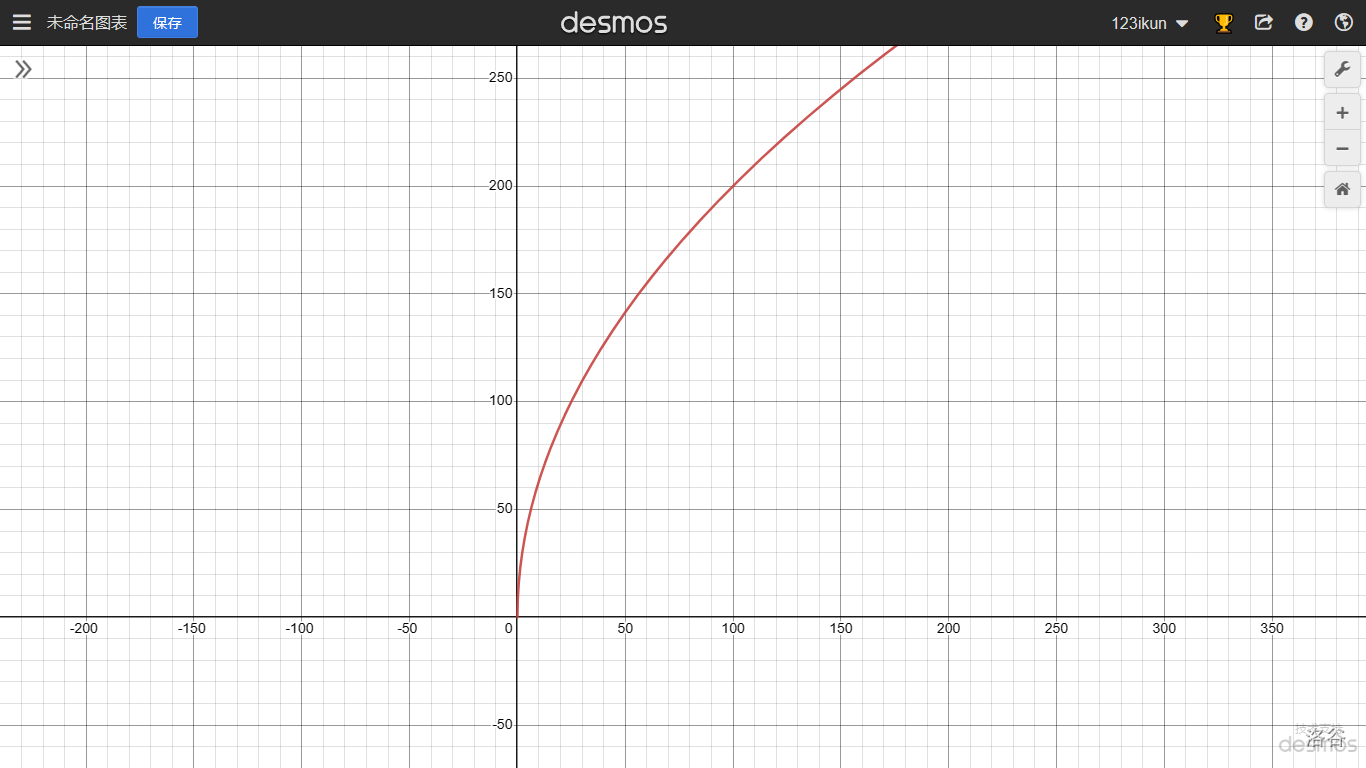
用几个式子来表示一个(不是几个!)函数,不仅与函数定义并无矛盾,而且有现实意义。在自然科学和工程技术中,经常会遇到分段函数的情形。例如在[等温过程](https://baike.sogou.com/v8755287.htm#:~:text=%E7%AD%89%E6%B8%A9%E8%BF%87%E7%A8%8B%EF%BC%88%E8%8B%B1%E8%AF%AD%EF%BC%9AIsothermal%20process%EF%BC%89%E6%98%AF%E7%83%AD%E5%8A%9B%E5%AD%A6%E8%BF%87%E7%A8%8B%E7%9A%84%E4%B8%80%E7%A7%8D%EF%BC%8C%E5%85%B6%E4%B8%AD%E7%B3%BB%E7%BB%9F%E7%9A%84%E6%B8%A9%E5%BA%A6%E4%B8%8D%E5%8F%98%EF%BC%9A%CE%94T,%3D%200%E3%80%82%20%E4%B8%80%E4%B8%AA%E7%B3%BB%E7%BB%9F%E4%B8%8E%E5%A4%96%E7%95%8C%E7%9A%84%E7%83%AD%E6%BA%90%EF%BC%88%E7%83%AD%E6%B5%B4%EF%BC%89%E6%8E%A5%E8%A7%A6%EF%BC%8C%E8%80%8C%E8%BF%87%E7%A8%8B%E8%BF%9B%E8%A1%8C%E5%BE%97%E8%B6%B3%E5%A4%9F%E7%BC%93%E6%85%A2%EF%BC%8C%E4%BD%BF%E5%BE%97%E7%B3%BB%E7%BB%9F%E4%B8%8D%E6%96%AD%E9%80%9A%E8%BF%87%E7%83%AD%E4%BA%A4%E6%8D%A2%E6%8A%8A%E6%B8%A9%E5%BA%A6%E8%B0%83%E6%95%B4%E4%B8%BA%E4%B8%8E%E7%83%AD%E6%BA%90%E7%9A%84%E6%B8%A9%E5%BA%A6%E7%9B%B8%E5%90%8C%EF%BC%8C%E5%88%99%E8%BF%99%E4%B8%AA%E8%BF%87%E7%A8%8B%E5%B0%B1%E6%98%AF%E7%AD%89%E6%B8%A9%E8%BF%87%E7%A8%8B%E3%80%82)中,气体压强 $p$ 与体积 $V$ 的函数关系,当 $V$ 不太小时依从玻意耳(Boyle)定律;当 $V$ 相当小时,函数关系就要用范德瓦耳斯(van der Waals)方程来表示,即
$$p=\begin{cases}\dfrac{\gamma}{V-\beta}-\dfrac{\alpha}{V^2}&\beta<V<V_0\\\dfrac{k}{V}&V\geqslant V_0\end{cases}$$
其中$k$,$\alpha$,$\beta$,$\gamma$ 都是常量。
2. 函数的几种特性
(1)**函数的有界性**
$\quad$ 设函数 $f(x)$ 的定义域为 $D$,数集 $X \subset D$。如果存在数 $K_1$,使得
$$f(x)\geqslant K_1$$
对任一 $x\in X$ 都成立,那么称函数 $f(x)$ 在 $X$ 上有**上界**,而 $K_1$ 称为函数 $f(x)$ 在 $X$ 上的一个上界。如果存在数 $K_2$,使得
$$f(x) \leqslant K_2$$
对任意 $x\in X$ 都成立,那么称函数 $f(x)$ 在 $X$ 上有**下界**,而 $K_2$ 称为函数 $f(x)$ 在 $X$ 上的一个下界。如果存在 正数 $M$,使得
$$|f(x)|\leqslant M$$
对任一 $x\in X$ 都成立,那么称函数 $f(x)$ 在 $X$ 上**有界**。如果这样的$M$ 不存在,就称函数 $f(x)$ 在$X$ 上**无界**;这就是说,如果对于任一正数 $M$ ,总存在 $x_1\in X$,使$|f(x_1)|>M$,那么函数 $f(x)$ 在 $X$ 上无界。
例如,就函数 $f(x)=\sin x$ 在 $(-\infty,+\infty)$ 内来说,数 $1$ 是它的一个上界,数 $-1$ 是它的一个下界(当然,大于 $1$ 的任何数也是它的上界,小于 $-1$ 的任何数也是它的下界)。又
$$ | \sin x| \leqslant 1 $$
对任一实数 $x$ 都成立,故函数 $f(x)=\sin x$ 在 $(-\infty,+\infty)$ 内也是有界的,这里 $M=1$ (当然也可取大于 $1$ 的任何数作为$M$ 而使 $|f(x)|\leqslant M$ 对任一实数都成立)。
又如函数 $f(x)=\dfrac{1}{x}$ 在[开区间](https://baike.baidu.com/item/%E5%BC%80%E5%8C%BA%E9%97%B4/9594680)$(0,1)$ 内没有上界,但有下界,例如 $1$ 就是它的一个下界。函数 $f(x)=\dfrac{1}{x}$ 在开区间 $(0,1)$ 内是无界的,因为不存在这样的正数 $M$,使 $|\dfrac{1}{x}|\leqslant M$ 对于 $(0,1)$ 内的一切 $x$ 都成立。但是 $f(x)=\dfrac{1}{x}$ 在区间 $(1,2)$ 内是有界的,例如可取 $M=1$ 而使 $|\dfrac{1}{x}|\leqslant 1$ 对于一切 $x\in(1,2)$ 都成立。
容易证明,函数 $f(x)$ 在 $X$ 上有界的[充要条件(充分必要条件)](https://baike.baidu.com/item/%E5%85%85%E5%88%86%E5%BF%85%E8%A6%81%E6%9D%A1%E4%BB%B6?fromtitle=%E5%85%85%E8%A6%81%E6%9D%A1%E4%BB%B6&fromid=6906972&fromModule=lemma_search-box)是它在 $X$ 上既有上界又有下界。
**(2)函数的单调性**
$\quad$设函数 $y=f(x)$ 的定义域为 $D$,区间 $I\subset D$。如果对于区间$I$ 上任意两点 $x_1$ 和 $x_2$ 时,恒有
$$f(x_1)<f(x_2)$$
那么称函数 $y=f(x)$ 在区间 $I$ 上是**单调增加**的见下图
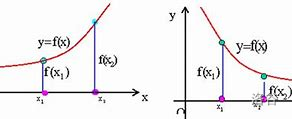
如果对于区间 $I$ 上任意两点 $x_1$ 和 $x_2$ ,当 $x_1<x_2$ 时,恒有
$$f(x_1)>f(x_2)$$
那么称函数 $y=f(x)$ 在区
$\quad$ 例如,函数 $y=x^2$ 在区间 $[0,+\infty)$ 上是单调增加的,在区间 $(-\infty,0]$ 上是单调减少的;在区间 $(-\infty ,+\infty)$ 内函数 $y=x^2$ 不是单调的,如下图:
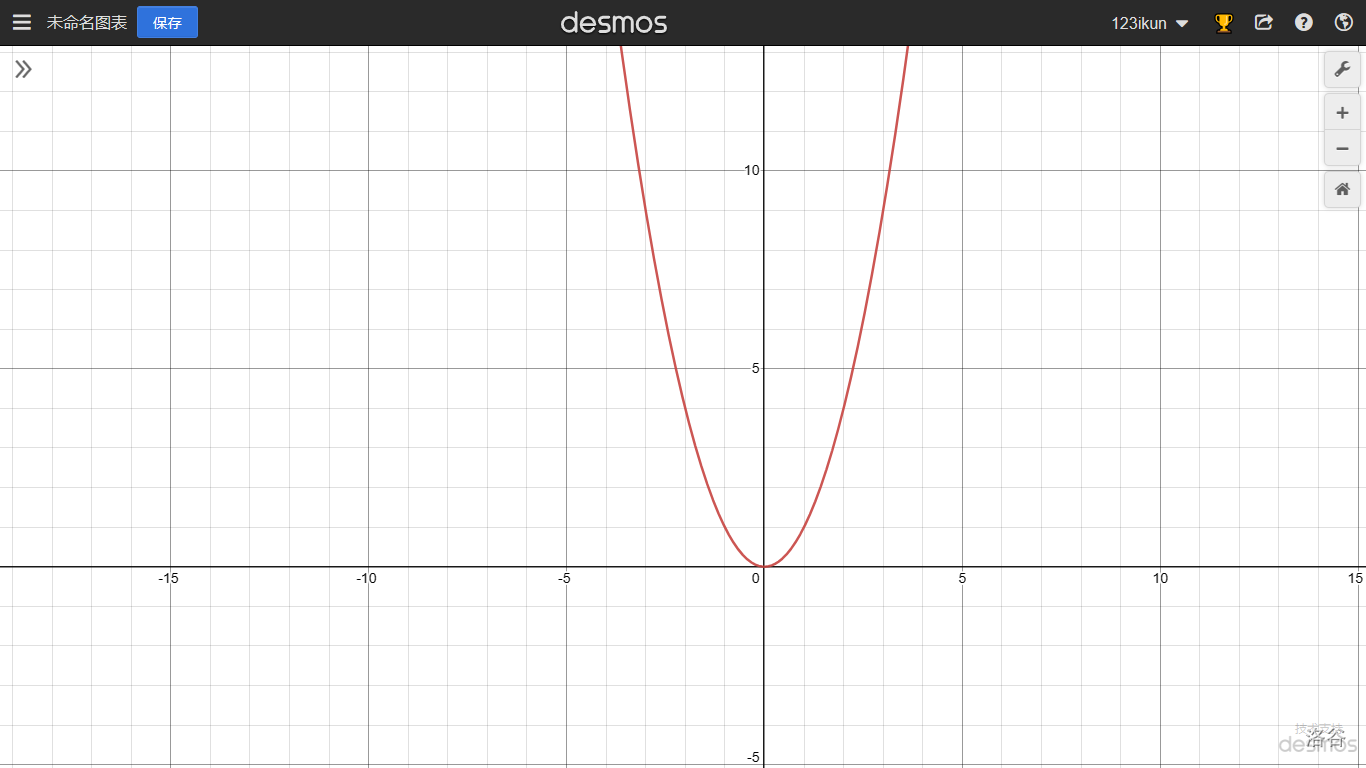
又例如,函数 $y=x^3$ 在区间 $(-\infty,+\infty)$ 内是单调增加的,如下图:
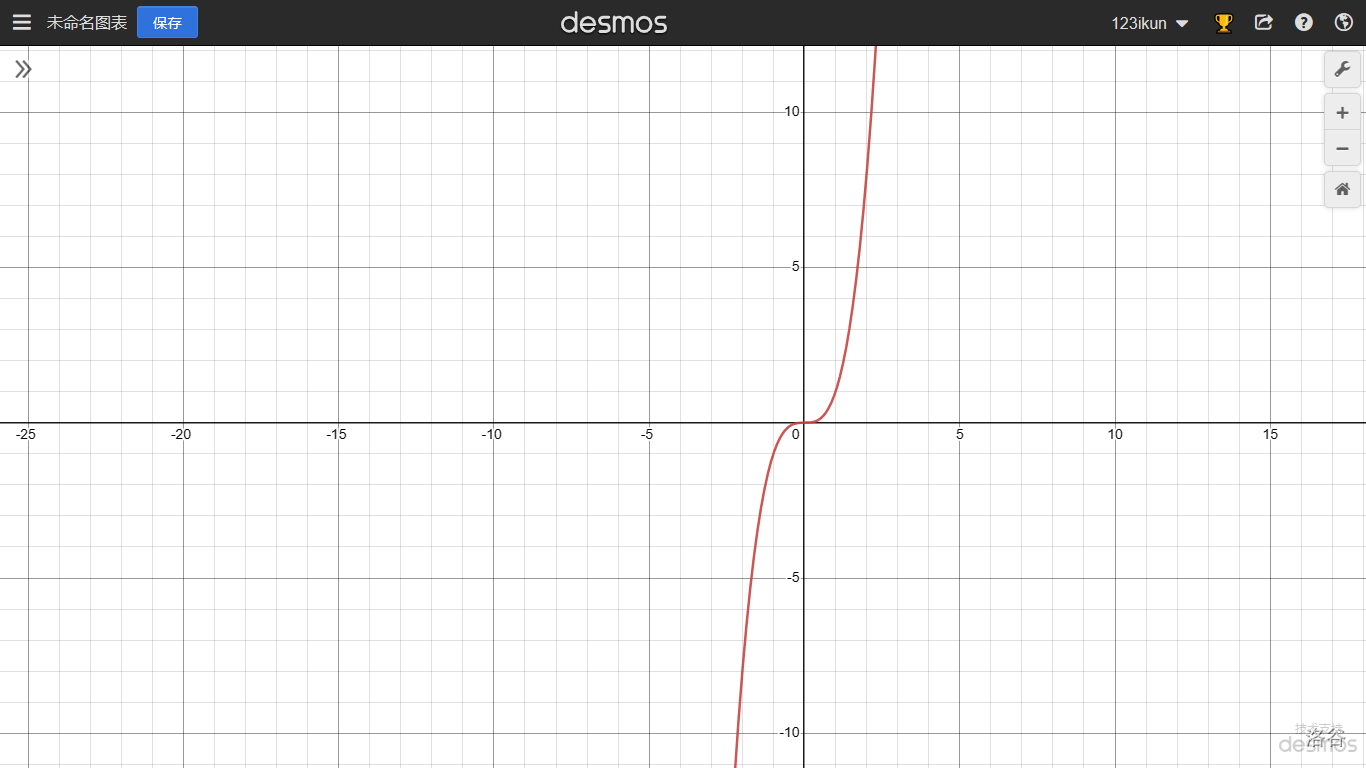
**(3) 函数的奇偶性**
$\quad$ 设函数 $f(x)$ 的定义域 $D$ 关于[原点对称](https://baike.baidu.com/item/%E5%8E%9F%E7%82%B9%E5%AF%B9%E7%A7%B0/6622352)。如果对于任一 $x\in D$,
$$f(-x)=f(x)$$
恒成立,那么称 $f(x)$ 为**偶函数**。如果对于任一 $x\in D$,
$$f(-x)=-f(x)$$
恒成立,那么称 $f(x)$ 为**奇函数**。
$\quad$ 例如,$f(x)=x^2$ 是偶函数,因为 $f(-x)=(-x)^2=x^2=f(x)$。又例如,$f(x)=x^3$ 是奇函数,因为 $f(-x)=(-x)^3=-x^3=-f(x)$。
$\quad$ 偶函数的图形关于 $y$ 轴是对称的。因为若 $y=f(x)$ 是偶函数,则 $f(-x)=f(x)$,所以如果 $A(x,f(x))$ 是图形上的点,那么它关于 $y$ 轴对称的点 $A'(-x,f(x))$ 也在图形上。
$\quad$ 奇函数的图形关于原点是对称的。因为若 $y=f(x)$ 是奇函数,则 $f(-x)=-f(x)$,所以如果 $A(x,f(x))$ 是图形上的点,那么它关于原点对称的点 $A"(-x,-f(x)$ 也在图形上。
函数 $y=\sin x$ 是奇函数。函数 $y=\cos x$ 是偶函数。 函数 $y=
sin x+\cos x$ 既非奇函数,也不是偶函数。
**(4) 函数的周期性** $\quad$ 设函数 $f(x)$ 的定义域为 $D$。如果存在一个正数 $l$,使得对于任一 $x\in D$ 有 $(x \pm D)\in D$,且
$$f(x+l)=f(x)$$
成立,那么称 $f(x)$ 为**周期函数**,$l$ 称为 $f(x)$ 的**周期**,通常我们说周期函数的**周期**是指**最小正周期**。
$\quad$ 例如,函数 $y=\sin x,y=\cos x$ 都是以 $2\pi$ 为周期的周期函数;函数 $t=\tan x$ 是以 $\pi$ 为周期的周期函数。
下图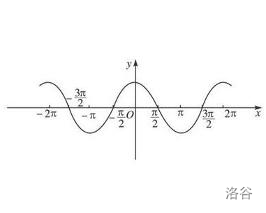
表示周期为 $l$ 的一个周期函数。在每个长度为 $l$ 我的区间上,函数图形有相同的形状。
$\quad$ 并非每个周期函数都有最小正周期。下面的函数就属于这种情形
狄利克雷(Dirichlet)函数
$$D(x)=\begin{cases}1&x\in Q\\0&x\in Q^C\end{cases}$$
容易验证这是一个周期函数,任何正有理数 $r$ 都是它的周期。因为不存在最小的正有理数,所以它没有最小正周期。
3. 反函数和复合函数
作为逆映射的特例,我们有以下反函数的概念:
$\quad$ 设函数 $f:D\to f(D)$ 是单射,则它存在逆映射 $f^{-1} : f(D) \to D $,则称此映射 $f^{-1}$ 为函数 $f$ 的**反函数。
$\quad$ 按此定义,对每个 $y\in f(D)$ ,有唯一的 $x\in D$ 使得 $f(x)=y$,于是有
$$f^{-1}(y)=x$$
这就是说,反函数 $f^{-1}$ 的对应法则是完全由函数 $f$ 的对应法则所确定的。
$\quad$ 例如,函数 $y=x^3,x\in R$ 是单射,所以他的反函数存在,其反函数为 $x=y^{\frac{1}{3}},y\in R$ 。
$\quad$ 由于习惯自变量用 $x$ 表示,因变量用 $y$ 表示,于是 $y=x^3,x\in R$ 的反函数通常写作 $x=y^{\frac{1}{3}},y\in R
$\quad$ 若 $f$ 是定义在 $D$ 上的单调函数,则 $f:D\to f(D)$ 是单射,于是 $f$ 的反函数 $f^{-1}$ 必定存在,而且容易证明 $f^{-1}$ 也是 $f(D)$ 上的单调函数。事实上,我们不妨设 $f$ 在 $D$ 上单调增加,现在来证明 $f^{-1}$ 在 $f(D)$ 上也是单调增加的。
$\quad$ 任取 $y_1,y_2\in f(D)$,且 $y_1<y_2$。按函数 $f$ 的定义,对 $y_1$,在 $D$ 内存在唯一的原像 $x_1$,使 $f(x_1)=y_1$,于是 $f^{-1}(y_1)=x_1$;对 $y_2$,在 $D$ 内存在唯一的原像 $x_2$,使得 $f(x_2)=y_2$,于是 $f^{-1}(y_2)=x_2$。
$\quad$ 如果 $x_1>x_2$,则由 $f(x)$ 单调增加,必有 $y_1>y_2$;如果 $x_1=x_2$,则显然有 $y_1=y_2$。这两种情形都与假设 $y_1<y_2$ 不符,故必有 $x_1<x_2$ ,即 $f^{-1}(y_1)<f^{-1}(y_2)$。这就证明了 $f^{-1}$ 在 $f(D)$ 上是单调增加的。
$\quad$ 相对于反函数 $y=f^{-1}(x)$ 来说,原来的函数 $y=f(x)$ 称为**直接函数**。把直接函数 $y=f(x)$ 和他的反函数 $y=f^{-1}(x)$ 的图形画在同一坐标平面上,这两个图形关于直线 $y=x$ 是对称的。如下图: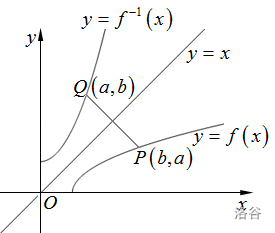
这是因为如果 $P(a,b)$ 是 $y=f(x)$ 图形上的点,则有 $b=f(a)$。按反函数的定义,有 $a=f^{-1}(b)$,故 $Q(b,a)$ 是 $y=f^{-1}(x)$ 图形上的点;反之,若 $Q(b,a)$ 是 $y=f^{-1}(x)$ 图形上的点,则 $P(a,b)$ 是 $y=f(x)$ 图形上的点。而 $P(a,b)$ 与 $Q(b,a)$ 是关于直线 $y=x$ 对称的。
$\quad$ 复合函数是复合映射的一种特例,按照通常函数的记号,复合函数的概念可如下表述:
$\quad$ 设函数 $y=f(u)$ 的定义域为 $D_f$,函数 $u=g(x)$ 的定义域为 $d_g$,且其值域 $R_g \subset D_f$,则由下列式子确定的函数
$$y=f[g(x)],x\in D_g$$
称为由函数 $u=g(x)$ 与函数 $y=f(u)$ 构成的**复合函数**,它的定义域为 $D_g$,变量 $u$ 称为**中间变量**
$\quad$ 函数 $g$ 与函数 $f$ 构成的复合函数,即按“先 $g$ 后 $f$”的次序复合的函数,通常即 $fog$,即
$$(fog)(x)=f[g(x)]$$
$\quad$ 与复合映射一样,$g$ 与 $f$ 能构成复合函数 $fog$ 的条件是:函数 $g$ 的值域 $R_g$ 必须包含与函数 $f$ 的定义域 $D_f$,即 $r_g \subset D_f$。否则,不能构成复合函数。例如,$y=f(u)=\arcsin u$ 的定义域为 $[-1,1]$,$u=g(x)=\sin x$ 的定义域为 $R$,且 $g(R)\subset [-1,1]$,故 $g$ 与 $f$ 可构成复合函数
$$y=\arcsin \quad \sin x,x\in R;$$
又如,$y=f(u)=\sqrt{u}$ 的定义域为 $d_f=[0,+\infty),u=g(x)=\tan x$ 的值域为 $R_g=(-\infty,+\infty)$,显然 $R_g\not\subset D_f$,故 $g$ 和 $f$ 不能构成复合函数。但是,如果将函数$g$ 限制在它的定义域的一个子集$D=\begin{Bmatrix}x|k\pi\leqslant x<\begin{pmatrix}k+\frac{1}{2}\end{pmatrix} \pi,k\in Z\end{Bmatrix}$ 上,令 $g^*(x)=\tan x,x\in D$,那么 $R_{g^*}=g^*(D)\subset D_f,g^*$ 与 $f$ 就可以构成复合函数
$$(fog^*)(x)=sqrt{\tan x},x \in D$$
$\quad$ 习惯上为了简便起见,仍称函数 $\sqrt{\tan x}$ 是由函数 $u=\tan x$ 与函数 $y=\sqrt{u}$ 构成的复合函数。这里函数 $u=\tan x$ 应理解成:$u=\tan x,x\in D$。以后的文章,我都采取这种习惯说法,例如,我们称函数 $u=x+1$ 与函数 $y=\ln u$ 构成复合函数 $\ln(x+1)$,它的定义域不是 $u=x+1$ 的自然定义域 $R$,而是 $R$ 的一个子集 $D=(-1,+\infty)$。
$\quad$ 有时,也会遇到两个以上函数所构成的复合函数,只要它们顺次满足构成复合函数的条件。例如,函数 $y=\sqrt{u},u=\cot v,v=\frac{x}{2}$ 可构成复合函数 $y=\sqrt{\cot \frac{x}{2}}$,这里 $u$ 及 $v$ 都是中间变量,复合函数的定义域是 $D=\begin{Bmatrix}x|2k\pi <x\leqslant(2k+1)\pi,k\in Z\end{Bmatrix}$,而不是 $v=\frac{x}{2}$ 的自然定义域 $R$, $D$ 是 $R$ 的一个非空子集。
4. 函数的运算
$\quad$ 设函数 $f(x),g(x)$ 的定义域依次为 $D_f,D_g,D=D_f\cap D_g\ne \varnothing$,则我们可以定义这两个函数的下列运算:
和(差)$f\pm g:\quad (f\pm g)(x)=f(x)\pm g(x),x\in D
积 f\cdot g:\quad (f\cdot g)(x)=f(x)\cdot g(x),x\in D
商 \frac{f}{g}:\quad \left(\dfrac{f}{g}\right)(x)=\frac{f(x)}{g(x)},x\in D\backslash\left\{x|g(x)=0,x\in D\right\}
例:\quad 设函数f(x) 的定义域为 (-l,l),证明必存在 (-l,l) 上的偶函数 g(x) 及奇函数 h(x),使得
f(x)=g(x)+h(x)
证 \quad 先分析如下:假若这样的 g(x),h(x) 存在,使得
f(x)=g(x)+h(x)\quad(1-1)
且
g(-x)=g(x),h(-x)=-h(x)
于是有
f(-x)=g(-x)+h(-x)=g(x)-h(x)\quad (1-2)
利用(1-1),(1-2) 式,就可做出 g(x),h(x)。这就启发我们作如下证明:
作
g(x)=\frac{1}{2}[f(x)+f(-x)],h(x)=\frac{1}{2}[f(x)-f(-x)]
则
g(x)+h(x)=f(x),
g(-x)=\frac{1}{2}[f(-x)+f(x)]=g(x),
h(-x)=\frac{1}{2}[f(-x)-f(x)]=-h(x).
证毕.
- 初等函数
在初等数学中已经讲过下面几类函数:
幂函数:y=x^\mu(\mu\in R 是常数),
指数函数:y=a^x(a>0 且 a\ne1)。
对数函数:y=log_a x(s>0 且 a\ne1, 特别当 a=e 时,记作 y=\ln x)(e 的解释)
三角函数:如y=\sin x,y=\cos x,y=\tan x,y=\arctan x 等。
以上四类函数统称为基本初等函数。
由常数和基本初等函数经过有限次的四则运算和有限次的函数复合步骤所构成并可用一个式子表示的函数,称为初等函数例如:
y=\sqrt{1-x^2},y=\sin^2 x,y=\sqrt{\cos \frac{x}{2}}
等都是初等函数。本文章中大多数函数都是初等函数。
后语:本文参考《高等数学》第一章。如果有错,请大佬指正。(内心os:md,这玩意费了我10个晚上。。。以后也不写了,累死了)
哦,对了,如果看不懂,或者想了解更多的关于函数的知识,可以去B站关注一下宋浩老师,我只是对函数进行一个简单的解说,宋浩老师更全面!
如果想了解更多关于高数的知识,可以去B站的这里看一下,这个老师也挺不错。
也可以去知乎关注一下丙陆数理,这个人讲的比我讲的还“干货”。让我先学一下数列的极限,争取2个月给你们出下一期!
本文结!