CSP提高组 赛前摸测总结大全
__H_J_M__
·
·
个人记录
CSP提高组 赛前摸测1
T1 序列
## T2 生成最小树
__题意:__
__描述__
你有一个含n个点、m条边的图。现在选出一棵生成树,你每次可以选择树上一条边使其边权减1,问至少需要操作多少次之后这棵树会成为图的最小生成树?保证图完全连通且不含重边。
注:图中节点编号从1到n。
__输入描述__
第一行输入两个数n,m,分别表示图的点数和边数;(1≤n≤10000,1≤m≤100000)
之后m行,每行三个数u,v,w,表示从点u到点v的连边权值为w;
之后n−1行,每行两个数a,b,表示选定生成树的每条边。
__输出描述__
输出一个数,表示最少的操作次数。
__解题思路:__
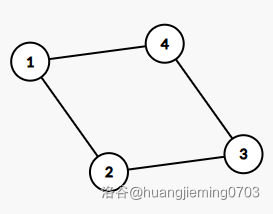
如图,如果边(1,2),(2,3),(3,4)为最小生成树上边。
如果其中任意一条边大于边(1,4),即可以进行替换,因此显然我们应当满足:任意一条非树边和其他树上边组成的环中,树上边的边权应当小于非树边,及(1,2),(2,3),(3,4)<(1,4)
即可提出暴力做法,每一次进行一次暴力搜索,进行判断。O(N*N)
__优化:__
我们可以对所有非树边进行按边权的排序,我们可以发现树边不用枚举第二次,如图:
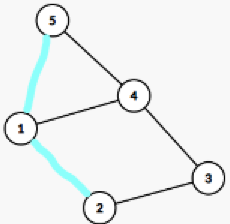
当前依次枚举(1,2),(1,5)
当枚举完(1,2)后,可以满足,(1,2)>(1,4)
因为(1,2)<(1,5),因而(1,4)<(1,5),因而不用枚举第二次:
可以使用LCA和路径压缩解决:
__代码:__
```cpp
#include <bits/stdc++.h>
#define int long long
#define PII pair<long long,long long>
using namespace std;
/*!@#$%^&*!@#$%^&*~~优美的分界线~~*&^%$#@!*&^%$#@!*/
const int N=1e4+5,M=1e5+5;
int n,m;
int ans;
int h[N],f[N],w[N];//当前树上点的深度,点的父亲,点到父亲的距离
vector<int> v[N];
map< PII , int > mp;
map< PII , bool > mp2;
struct tree{
int a,b,c;
bool operator < (const tree& a){
return c<a.c;
}
}l[M];
/*!@#$%^&*!@#$%^&*~~优美的分界线~~*&^%$#@!*&^%$#@!*/
void dfs(int x,int fa,int dep){
h[x]=dep;
for(int i=0;i<v[x].size();i++){
int y=v[x][i];
if(fa==y) continue;
f[y]=x,w[y]=mp[make_pair(x,y)];
dfs(y,x,dep+1);
}
}
void push_up(int x,int W){
if(w[x]<=W) return;
ans+=w[x]-W;
w[x]=W;
}
int LCA(int x,int y,int w){
if(x==y) return x;
int lca=0;
if(h[f[x]]==h[f[y]]){
push_up(x,w);
push_up(y,w);
lca=LCA(f[x],f[y],w);
}
if(h[f[x]]>h[f[y]]){
push_up(x,w);
lca=LCA(f[x],y,w);
}
if(h[f[x]]<h[f[y]]){
push_up(y,w);
lca=LCA(x,f[y],w);
}
if(lca!=x) f[x]=lca;
if(lca!=y) f[y]=lca;
return lca;
}
/*!@#$%^&*!@#$%^&*~~优美的分界线~~*&^%$#@!*&^%$#@!*/
signed main(){
freopen("mintree.in","r",stdin);
freopen("mintree.out","w",stdout);
cin>>n>>m;
for(int i=1;i<=m;i++){
cin>>l[i].a>>l[i].b>>l[i].c;
mp[make_pair(l[i].a,l[i].b)]=l[i].c;
mp[make_pair(l[i].b,l[i].a)]=l[i].c;
}
sort(l+1,l+m+1);
for(int i=1;i<n;i++){
int a,b;cin>>a>>b;
v[a].push_back(b);
v[b].push_back(a);
mp2[make_pair(a,b)]=1;
mp2[make_pair(b,a)]=1;
}
f[1]=1;
dfs(1,0,1);
for(int i=1;i<=m;i++){
if(mp2[make_pair(l[i].a,l[i].b)]==1) continue;
LCA(l[i].a,l[i].b,l[i].c);
}
cout<<ans;
return 0;
}
```
# T3
由于 *a* 与 *b* 之间的差不超过 100,因此他们所拥有的共同的质因子,也不会超过 100,而 100 以内的质数共有 25个,因此考虑状压 $dp$。
尽管 *a*,*b* 的范围有 $1e18$,但我们并不需要知道每个数所有的质因子,只需要得到 100 以内的质因子,就可以进行状态转移了。
定义 $dp[i][s]$ 表示最大的数不超过 $a+i$,对应的质因子选择的状态为 $s$ 的序列数量。
每加入一个新的数 $i$,有选和不选两种情况:
1.如果选择 $i$,则可以从 $i-1$ 的所有不包括 $i$ 的质因子的状态做状态转移。
2.如果不选择 $i$,则直接从 $i-1$ 转移到 $i$。
但是,注意到大于 50 的质因子,可能只出现 1 次,不需要记录状态,因此状态不需要到 25,开 22 即可,核心是剔除掉只出现 1 次的质因子。
这是一个更为优秀的时间复杂度,可以通过。
__代码:__
```cpp
#include <bits/stdc++.h>
#define int long long
using namespace std;
/*!@#$%^&*!@#$%^&*~~优美的分界线~~*&^%$#@!*&^%$#@!*/
int A,B;
int num[25];
int f[1<<23];
vector<int> v;
int pre[25]={2,3,5,7,11,13,17,19,23,29,31,37,
41,43,47,53,59,61,67,71,73,79,83,89,97};
/*!@#$%^&*!@#$%^&*~~优美的分界线~~*&^%$#@!*&^%$#@!*/
/*!@#$%^&*!@#$%^&*~~优美的分界线~~*&^%$#@!*&^%$#@!*/
signed main(){
freopen("rlprime.in","r",stdin);
freopen("rlprime.out","w",stdout);
cin>>A>>B;
for(int i=A;i<=B;i++){
for(int j=0;j<25;j++)
if(i%pre[j]==0)
num[j]++;
}
for(int i=0;i<25;i++)
if(num[i]>1)
v.push_back(pre[i]);
f[0]=1;
for(int i=A;i<=B;i++){
int s=0;
for(int j=0;j<v.size();j++)
if(i%v[j]==0)
s|=(1<<j);
int S=((1<<v.size())-1)^s;
for(int j=S;j;j=(j-1)&S){
f[s|j]+=f[j&S];
}
f[s]+=f[0];
}
//1100
//1001
//1010
//1000
int ans=0;
for(int i=0;i<(1<<v.size());i++)
ans+=f[i];
cout<<ans-1;
return 0;
}
```
# CSP提高组 赛前摸测2
__题目解释:__
[更好的阅读体验](https://www.luogu.com.cn/team/98570#file)
nothing else
__做题情况:__
## T1 score and rank
$50$分,错了一个小小的地方
```cpp
#include <bits/stdc++.h>
#define int long long
using namespace std;
/*!@#$%^&*!@#$%^&*~~优美的分界线~~*&^%$#@!*&^%$#@!*/
const int N=1e6+5;
int n,s;
int sum;
int ans,v[N];
priority_queue<int> q1,d1;//大根堆
priority_queue< int,vector<int>,greater<int> > q2,d2;//小根堆
/*!@#$%^&*!@#$%^&*~~优美的分界线~~*&^%$#@!*&^%$#@!*/
int read(){
int s=0,f=1;char ch=getchar();
while(ch<'0'||ch>'9') {if(ch=='-') f=-1;ch=getchar();}
while(ch>='0'&&ch<='9') s=(s<<3)+(s<<1)+(ch^48),ch=getchar();
return s*f;
}
void clean(){
while(!q1.empty()) q1.pop();
while(!q2.empty()) q2.pop();
while(!d1.empty()) d1.pop();
while(!d2.empty()) d2.pop();
}
void Del(int x,int &sum){//消除x对sum的影响
sum-=x;
while(x){
while(!d2.empty()&&q2.top()==d2.top())
q2.pop(),d2.pop();
if(x>=q2.top()){
x-=q2.top();
d1.push(q2.top());
q2.pop();
}else{
int nw=q2.top()-x;
q1.push(nw);
d1.push(q2.top());
q2.pop();
q2.push(nw);
break;
}
}
}
void push(int x,int &sum){
q1.push(x),q2.push(x);
sum+=x;
while(sum>=s){
while(!d1.empty()&&q1.top()==d1.top())
q1.pop(),d1.pop();
sum-=q1.top();
d2.push(q1.top());
q1.pop();
ans++;
}
}
/*!@#$%^&*!@#$%^&*~~优美的分界线~~*&^%$#@!*&^%$#@!*/
signed main(){
freopen("score.in","r",stdin);
freopen("score.out","w",stdout);
cin>>n>>s;
for(int i=1;i<=n;i++) v[i]=read();
if(s<=0){
for(int i=1;i<=n;i++) ans+=(v[i]>=s);
cout<<ans;
}else{
for(int i=1;i<=n;i++){
int x=v[i];
if(sum+x<=0){
clean();
sum=0;
}else{
if(x>0) push(x,sum);
else Del(-x,sum);
}
}
cout<<ans;
}
return 0;
}
```
## T2 松鼠大作战
$20$分,暴力
```cpp
#include <bits/stdc++.h>
#define ll long long
using namespace std;
/*!@#$%^&*!@#$%^&*~~优美的分界线~~*&^%$#@!*&^%$#@!*/
const int N=2e5+5;
int n,q;
int a[N];
int dep[N],f[N][20];
vector<int> v[N];
/*!@#$%^&*!@#$%^&*~~优美的分界线~~*&^%$#@!*&^%$#@!*/
void dfs(int x,int fa){
dep[x]=dep[fa]+1;
if(a[fa]<=a[x]){
int nxt=fa;
for(int i=18;i>=0;i--)
if(a[f[nxt][i]]<=a[x]) nxt=f[nxt][i];
f[x][0]=f[nxt][0];
}else f[x][0]=fa;
for(int i=1;i<=18;i++)
f[x][i]=f[f[x][i-1]][i-1];
for(int i=0;i<v[x].size();i++){
int y=v[x][i];
if(fa==y) continue;
dfs(y,x);
}
}
int solve(int x,int y,int c){
int ans=a[x]>c;
for(int i=18;i>=0;i--)
if(a[f[x][i]]<=c) x=f[x][i];
if(dep[x]<=dep[y]) return ans;//怎么也跳不到
for(int i=18;i>=0;i--){
if(dep[f[x][i]]>=dep[y])
x=f[x][i],
ans+=(1<<i);
}
return ans;
}
/*!@#$%^&*!@#$%^&*~~优美的分界线~~*&^%$#@!*&^%$#@!*/
signed main(){
freopen("squirrel.in","r",stdin);
freopen("squirrel.out","w",stdout);
cin>>n>>q;
a[0]=1e9;
for(int i=1;i<=n;i++) cin>>a[i];
for(int i=1;i<n;i++){
int x,y;cin>>x>>y;
v[x].push_back(y);
v[y].push_back(x);
}
dfs(1,0);
while(q--){
int x,y,c;cin>>x>>y>>c;
cout<<solve(x,y,c)<<'\n';
}
return 0;
}
```
## T3 小S的旅行
$5$分,骗分
## 滚
$0
CSP提高组 赛前摸测3
更好的阅读体验