虚树小记

> 虚树是处理树上点集问题的有力而直观的工具。 **提示** : 鉴于初次学习虚树的同学树论经验一般不丰富，建议初学者在一周目时不必同步关注形式化证明，优先感性理解虚树的形式以及核心算法。 $\color{blue}\Large\star$ 标记代表关键性质， $\color{red}\Large\star$ 标记代表扩展内容。 ------------ ## 定义 - 给定一棵无根树 $T$ ，定义点集 $S$ 的虚树（Virtual Tree）为 : 最小的，包含 $S$ 的 $T$ 的连通子图。 不难发现，虚树仍然是树。下面是两个虚树的例子，其中蓝色点为点集 $S$ ，带有红色边框的部分为虚树。  在处理与点集 $S$ 有关的问题时，我们希望复杂度是和 $O(|S|)$ 有关，而不是和整棵树的大小 $O(|T|)$ 有关。 但根据虚树的定义，较小的 $S$ 可能产生很大的虚树。（如 $T$ 为一条链， $S$ 为链的两个端点，此时虚树为整个 $T$ ） 所以，直接在未简化的虚树上统计并不能很好地优化复杂度。 考虑进一步挖掘虚树的性质，将其结构简化，使得信息量（需要处理的对象个数）降低到 $O(|S|)$ 级别。 ## 经典性质 不妨选定节点 $1$ 为根，将树 $T$ 变为有根树，点集的虚树也随之变为有根树。 - $\color{blue}\Large\star$ **性质①** 虚树中，儿子数 $\geq 2$ 的点的数目 $\leq |S|-1$ 。 **证明** : 在虚树上进行 `dfs` 。 称 $S$ 中的点为“关键点”。记 $D_u$ 为节点 $u$ 子树中的关键点集合。显然，所有在虚树中的 $u$ 的 $D_u$ 均不为空。 称儿子数 $\geq 2$ 的点为“分叉点”。 某个分叉点有至少两个子树，该点的 $D$ 集合相当于将子树的 $D$ 集合合并。（若自己是关键点，也会将自己并入） 总共合并的次数不多于 $|S|-1$ 次，故分叉点的个数也 $\leq |S|-1$。 这等价地意味着，虚树中无分叉链的条数 $\leq 2|S|-1$。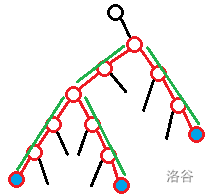（考虑所有关键点及分叉点的父边） 如图，$|S|=3$ 的点集产生的 $4$ 条无分叉链 :  - $\color{red}\Large\star$ **应用例** 动态开点 Trie 可以看做是维护了一棵完整的 Trie 的虚树。 于是，插入 $k$ 次的动态开点 Trie 的分叉点个数和无分叉链个数均为 $O(k)$。 该结论的一些应用 : - 证明后缀树的状态数是 $O(k)$ 的。 - 设计压缩 01Trie 。例 : [EA : 题解 P6136 【【模板】普通平衡树（数据加强版）】](https://www.luogu.com.cn/blog/EternalAlexander/solution-p6136) - 设计空间复杂度 $O(n)$ 的压缩线段树合并。 - **例题** : PKUSC2019 D1T3 **题意** : 给定长为 $n$ 的数组 $A$ 以及 $m$ 个询问 $(x_i,y_i)$ ，每次询问**是否**存在一个 $k$ 使得 $a_{x_i}$ 异或 $k$ 在所有数异或 $k$ 中排第 $y_i$ 。 $n\leq 5\times 10^4,m\leq 10^6,a_i\leq 2^{60}$。 首先用 $A$ 中的所有数建立 01Trie 。若 $k$ 的某一位为 $1$ ，则相当于将该层的所有点的左右儿子交换。 考虑如何处理单组询问。将 $A_x$ 祖先路径的分叉都找出来，可以通过调整 $k$ 使得某个分叉内的所有数小于或大于 $A_x$。 这就变成了一个可行性背包问题。 要对于每个 $A_x$ 求出答案，故问题等价于 : 给出一棵 01Trie ，求每个叶节点祖先路径的分叉大小的可行性背包。 对 01Trie 进行 `dfs` ，向某个分支走时，当前背包内加入另一个分支。 可行性背包可以利用 `bitset` 优化，又注意到有多个儿子的点（需要添加物品）的个数是 $O(n)$ 的，故总复杂度为 $O(n^2/w)$。 询问离线回答。 ------------ 根据 **性质①** ，若将虚树中的无分叉链简化成一条边，则虚树的状态量就会被简化到 $O(|S|)$ 级别，这正是我们想要的效果。 （当然，无分叉链简化成一条边的同时，链条中的信息也要进行简化，具体方式因具体题目而异） 为了方便，下文中，我们将简化后的虚树简称为“虚树”，而将原定义中的虚树改称为“完整虚树”。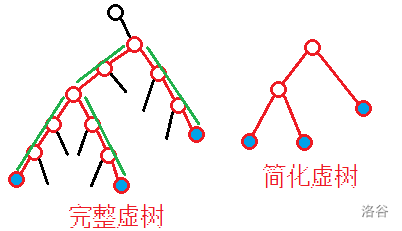  接下来，我们需要快速建立虚树。 首先找出虚树中的所有点。不难发现，多度点一定是两个关键点的 $\rm lca$ ，我们只需求集合 $\{{\rm lca}(u,v)|u,v\in S,u\neq v\}$ 即可得到所有多度点。 - $\color{blue}\Large\star$ **性质②** $\{{\rm lca}(u,v)|u,v\in S,u\neq v\}=\{{\rm lca}(u_i,u_{i+1})\}$ 其中 $u_i$ 按照 `dfs` 序从小到大排序。 **证明** : 首先显然有左边 $\supseteq$ 右边，那么只需证左边 $\subseteq$ 右边。 对于多度点 $t$ ，找出其（在虚树中）的所有直接儿子 $p_1,p_2,...p_m$ ，按 `dfs` 序排序。 任取其中相邻的两个儿子 $u,v$。找出 $u$ 子树内 `dfs` 序最大的关键点 $u'$，以及 $v$ 子树内 `dfs` 序最小的关键点 $v'$ ，则 $u',v'$ 是 `dfs` 序相邻的两个关键点，且有 ${\rm lca}(u',v')=t$。  因此，我们将关键点集合按照 `dfs` 序排序后，对相邻点求 $\rm lca$ （并去重）即可得到虚树中的点集。 - $\color{red}\Large\star$ **应用例** 几个相似的结论。 - 虚树边权和 / 链并 点集 $S=\{u_0,u_1,u_2,...u_{m-1}\}$ 的完整虚树的边权和可以这样计算 : $$\frac{1}{2}\sum\limits_{i=0}^{m-1}dis(u_i,u_{i+1\bmod m})$$ **例题** : [P3320 [SDOI2015]寻宝游戏](https://www.luogu.com.cn/problem/P3320) - 虚树式树上差分 若要对点集 $S$ 的完整虚树上的每个点加 $c$ ，可以进行如下操作 : 在每个 $u\in S$ 处 $+c$ ，在每个 $dis(u_i,u_{i+1\bmod m})$ 处 $-c$ ，最终做子树和即可得到答案。 **例题** : [[DS记录]Bzoj#4771. 七彩树](https://www.luogu.com.cn/blog/command-block/bzoj4771-qi-cai-shu) ------------ 接下来考虑如何连接虚树中的边。 将虚树点集 $S'=\{u_1,u_2,...u_m\}$ 按照 `dfs` 序排序后，有如下算法可以求出边集。 模拟对虚树进行 `dfs` 的过程，用栈维护根到当前点的路径。按照 `dfs` 序依次考虑各个点，当新加入点 $u$ 时，一直弹栈（回溯）直到 $u$ 在栈顶的子树内。将 $u$ 与栈顶连边，并入栈。 具体实现可见例题。 ## 经典实现 - **例题** : [P4103 [HEOI2014]大工程](https://www.luogu.com.cn/problem/P4103) **题意** : 给出树 $T$ ，边有边权，均为正。 多组询问，每次给出关键点集合 $S$ ，求下列式子的值 : $$ \begin{aligned} \sum\limits_{u\in S,v\in S,u\neq v}dis(u,v)\\ \max\limits_{u\in S,v\in S,u\neq v}dis(u,v)\\ \min\limits_{u\in S,v\in S,u\neq v}dis(u,v) \end{aligned} $$ 建立点集 $S$ 的虚树，将一条无分叉链简化为一条长度为链中所有边长度总和的边。 对于问题一，分别考虑每条边的贡献，系数为两侧关键点数目的乘积。 对于问题二，记 $f[u]$ 表示 $u$ 到子树内最远关键点的距离。对于每个点找出两个不同子树内的最远点进行转移。 对于问题三，记 $g[u]$ 表示 $u$ 到子树内最近关键点的距离。对于每个点找出两个不同子树内的最近点进行转移。 复杂度为 $O(n\log n)$。 ```cpp ``` - **更多例题** - [CF613D Kingdom and its Cities](https://www.luogu.com.cn/problem/CF613D) - [P2495 [SDOI2011]消耗战](https://www.luogu.com.cn/problem/P2495) - [P3233 [HNOI2014]世界树](https://www.luogu.com.cn/problem/P3233) - [P4242 树上的毒瘤](https://www.luogu.com.cn/problem/P4242) - [CF809E Surprise me!](https://www.luogu.com.cn/problem/CF809E) - [P4606 [SDOI2018]战略游戏](https://www.luogu.com.cn/problem/P4606) - [P7422 「PMOI-2」城市](https://www.luogu.com.cn/problem/P7422) ## 更精细的实现 考虑利用已按照 `dfs` 序排序的点集 $S$ 直接得到虚树。 仍然维护栈记录根到当前点的路径。 加入点 $u$ 时，分类讨论。 - 情况一 : $u$ 在栈顶 $top$ 的子树中。 直接将 $u$ 加入栈中。 - 否则 求 $t={\rm lca}(top,u)$ 。一直弹栈，直到 $t$ 在栈的次顶的子树内。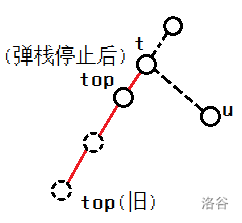 如图所示 :  红色为新连接的边。 - 情况二 : $t=top$ 直接将 $u$ 加入栈中。 - 情况三 : $t\neq top$ 如上图，此时将 $top$ 弹出，然后加入 $t,u$。连边 $t\rightarrow u$。 该算法的核心在于，按照 `dfs` 序加入时，新点所能接入的位置的总是一条右链，而随机插入时则可能在整颗树的任何位置。 若对随机插入时的情况感兴趣，可见 [题解 P6071 【[MdOI2020] Treequery】](https://www.luogu.com.cn/blog/command-block/solution-p6071) 该做法常数较小，且可以利用 $O(1)\ \rm LCA$ 在点集已经排序的情况下线性建立虚树。 ## 其他性质 & 套路 - $\color{red}\Large\star$ **分治与虚树** 在某些题目中，需要对点集进行分治的同时建立虚树。 此时，可以利用归并维护点集的 `dfs` 序，再利用上述算法线性建立虚树。相较于朴素的实现可以省去一个 $\log$。 另外一种方法是，自上而下建立，先建立原问题的虚树 $T$ ，再在 $T$ 上 `dfs` 建立两个子问题的虚树。（子问题中的虚树是原问题中的虚树的虚树） - **例题** - [[DS记录]P5439 【XR-2】永恒](https://www.luogu.com.cn/blog/command-block/ds-ji-lu-p5439-xr-2-yong-heng) - $\color{red}\Large\star$ **正权(完整)虚树的封闭性** 在**正边权**的树中，一个经典结论是 ： **点集直径的封闭性** 即 ： 对于点集 $S_1,S_2$ ，若直径分别为 $(u_1,v_1),(u_2,v_2)$ ，则点集 $S_1∪S_2$ 的直径端点必然在 $u_1,v_1,u_2,v_2$ 之中。 借由该结论，我们可以快速计算点集并的直径。 正权(完整)虚树的封闭性是一个更强的结论 ： 记 ${\rm val}(S)$ 为点集 $S$ 的完整虚树中的边权和。 定义某个点集 $S$ 的最大 $k$ 点虚树为 ： $|S|=k$ 且 ${\rm val}(S)$ 最大的 $S$。（当 $k=2$ 时即退化为直径） 对于点集合 $S_1,S_2$ ，若最大 $k$ 点虚树分别为 $T_1,T_2$ ，则点集 $S_1∪S_2$ 的最大 $k$ 点虚树必然在 $T_1∪T_2$ 之中。 下面介绍如何快速计算点集并的最大 $k$ 点虚树。 将点集 $T_1∪T_2$ 建立虚树，然后以点集直径的一端为根，将其长链剖分，选取前 $k-1$ 条长链即可。 正确性可见 ： [[DS记录]CF526G Spiders Evil Plan](https://www.luogu.com.cn/blog/command-block/ds-ji-lu-cf526g-spiders-evil-plan) - $\color{red}\Large\star$ **特殊图上的虚树** [[DS记录]P5360 [SDOI2019]世界地图](https://www.luogu.com.cn/blog/command-block/ds-ji-lu-p5360-sdoi2019-shi-jie-di-tu)