算法总结——差分(进阶)
program_xwl · · 算法·理论
既然是进阶,那当然要把基础内容学懂啊。
前面讲的是一次差分,在这里就要讲进阶版——二次差分啦。二次差分用于给数组中连续元素加上或减少等差的各项。 个人感觉没有一次差分实用
二次差分
问题描述:
有一个初始为全0 的数组a ,有T 次询问,对于每次询问,给出l、r、v、s ,需要将a_l+s,a_{l+1}+s+v,a_{l+2}+s+2v...a_r+s+kv 。
暴力法:
for(int i = l;i <= r;i++) a[i] += s+v*i;显然单次时间复杂度为O(n) ,总体时间复杂度为O(Tn) ,只能通过一些小范围的数据。
一次差分
由于每次加的量是变化的,所以我们不得不遍历一遍。
for(int i = l+1;i <= r;i++) diff[i] += v;
diff[r+1] -= v*(r-l);显然单次时间复杂度还是为O(n) ,总体时间复杂度为O(Tn) ,还是只能通过一些小范围的数据。
二次差分
我们先把a 数组和差分数组用表格列出来
设首项为s ,公差为v ,项数为5,末项为y 。
| 下标 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| 差分数组 |
屏幕前的你看到差分数组的那一排v ,肯定已经想到什么了。没错,二次差分就是用差分维护一个差分数组,这说起来可能有点绕,话不多说,我们把它用表列出来吧。
| 下标 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| 差分数组 | ||||||||
| 差分数组2(新增) |
可以看出差分数组2只有4个点发生了改变,其他还是0 。
于是,我们就得到了二次差分的更新方式:
-
diff_l + s -
diff_{l+1} - v-s -
diff_{r+1} - (y+v) -
diff_{r+2} + y 核心代码
diff[l] += s; diff[l+1] += v-s; diff[r+1] -= y+v; diff[r+2] += y;例题1 P4231 三步必杀
这题是二次差分模板题,不必多讲。
代码:
#include <bits/stdc++.h> using namespace std;
long long n,T,l,r,s,e,diff[10000005];
int main(void) { scanf("%lld %lld",&n,&T); while(T--) { scanf("%lld %lld %lld %lld",&l,&r,&s,&e); diff[l] += s; diff[l+1] += (e-s)/(r-l) - s; diff[r+1] -= e+(e-s)/(r-l); diff[r+2] += e; } for(int i = 1;i <= n;i++) diff[i] += diff[i-1]; for(int i = 1;i <= n;i++) diff[i] += diff[i-1]; long long ans1 = 0,ans2 = 0; for(int i = 1;i <= n;i++) ans1 ^= diff[i]; for(int i = 1;i <= n;i++) ans2 = max(ans2,diff[i]); printf("%lld %lld",ans1,ans2); return 0; }
## 例题2 [P5026 Lycanthropy](https://www.luogu.com.cn/problem/P5026)
### 题目描述太啰嗦了,可以画个图理解一下:
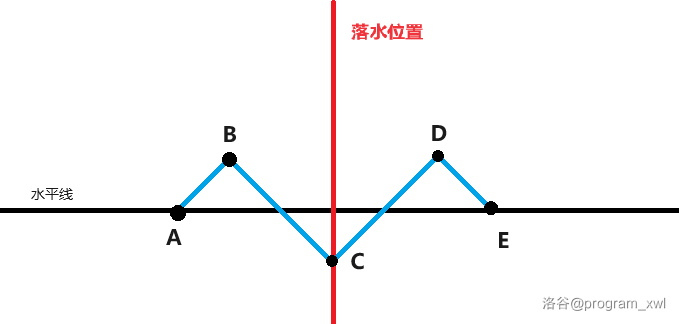
#### ~~哇!我发现了无限水!~~
#### 这题可以将线段AB、BC、CD、DE看作数组上的5条等差数列,按照上面的位置修改即可。不想判边界的话可以用偏移量,放心,空间允许。
### 代码:
```cpp
#include <bits/stdc++.h>
using namespace std;
int T,m,diff[3000005];
const int dis = 1000005;
int main(void)
{
cin >> T >> m;
while(T--)
{
int v,x;
cin >> v >> x;
diff[x-3*v+1+dis]++;
diff[x-2*v+1+dis]-=2;
diff[x+1+dis]+=2;
diff[x+2*v+1+dis]-=2;
diff[x+3*v+1+dis]++;
}
for(int i = 1;i <= m+dis;i++) diff[i] += diff[i-1];
for(int i = 1;i <= m+dis;i++) diff[i] += diff[i-1];
for(int i = 1;i <= m;i++) cout << diff[i+dis] << ' ';
return 0;
}