动态规划与记忆化搜索
kaiyuan
·
2019-09-28 15:23:50
·
个人记录
引入
采药(luogu P1048)
题解
直接写一个粗暴的 DFS :
int n,t;
int tcost[103],mget[103];
int ans = 0;
void dfs( int pos , int tleft , int tans ){
if( tleft < 0 ) return;
if( pos == n+1 ){
ans = max(ans,tans);
return;
}
dfs(pos+1,tleft,tans);
dfs(pos+1,tleft-tcost[pos],tans+mget[pos]);
}
int main(){
cin >> t >> n;
for(int i = 1;i <= n;i++)
cin >> tcost[i] >> mget[i];
dfs(1,t,0);
cout << ans << endl;
return 0;
}
尝试优化
不借助任何 "外部变量"(就是 dfs 函数外且 值随 dfs 运行而改变的变量 ), 比如 ans
把 ans 删了之后就有一个问题: 我们拿什么来记录答案?
答案很简单:
返回值!
此时 dfs(pos,tleft) 返回
在时间 tleft 内采集 后 pos 个草药, 能获得的最大收益
不理解就看看代码吧:
```cpp
int n,time;
int tcost[103],mget[103];
int dfs(int pos,int tleft){
if(pos == n+1)
return 0;
int dfs1,dfs2 = -INF;
dfs1 = dfs(pos+1,tleft);
if( tleft >= tcost[pos] )
dfs2 = dfs(pos+1,tleft-tcost[pos]) + mget[pos];
return max(dfs1,dfs2);
}
int main(){
cin >> time >> n;
for(int i = 1;i <= n;i++)
cin >> tcost[i] >> mget[i];
cout << dfs(1,time) << endl;
return 0;
}
```
emmmmmm....... 还是 ${\color{Red}30}$分
爆搜一无是处~
将所有 dfs 的返回值都记录下来,发现**对于相同的 pos 和 tleft,dfs 的返回值总是相同的!**
想一想也不奇怪, 因为**此时的 dfs 没有依赖任何外部变量.**
这就意味着,dfs重复做了很多次运算,浪费了很多时间。
为何这么说?
如图:
用递归的方法算斐波那契数列第五项(dfs主要思想就是递归),不优化的过程如下
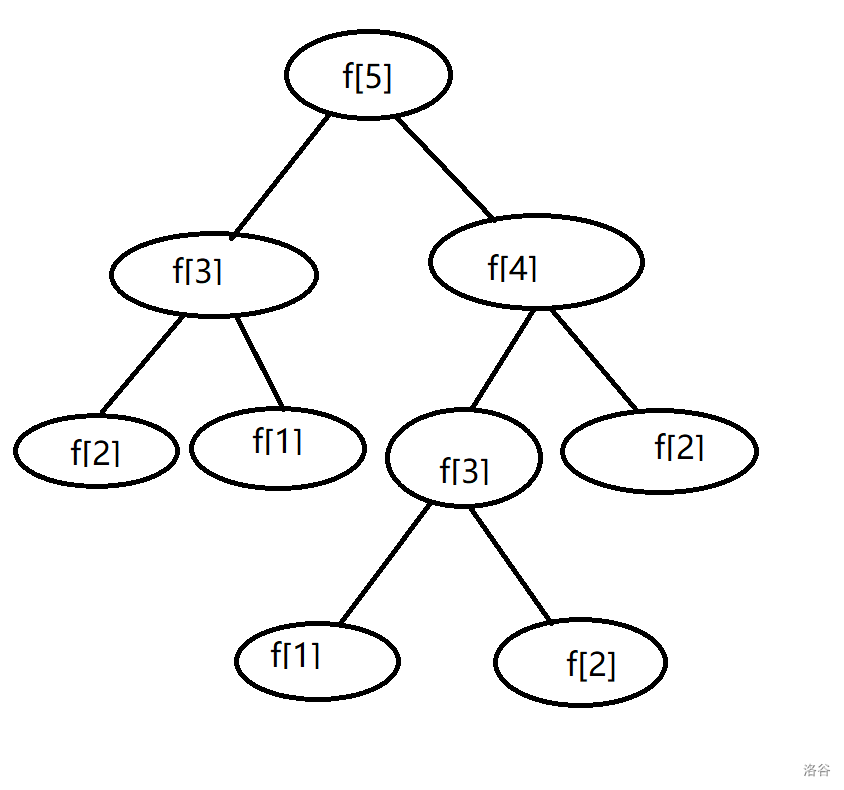
可以看出f[3]被重复计算了两次。
这只是第五项而已,如果是第一千项呢?时间极其浪费;
so,如何优化?
## 记忆化搜索
继续采药
开个数组 mem , 记录下来每个 dfs(pos,tleft) 的返回值. 刚开始把 mem 中每个值都设成 −1 (代表没访问过). 每次刚刚进入一个 dfs 前(我们的 dfs 是递归调用的嘛), 都检测 mem[pos][tleft] 是否为 −1 , 如果是就正常执行并把答案记录到 mem 中, 否则**直接返回 mem 中的值!**
```cpp
int n,t;
int tcost[103],mget[103];
int mem[103][1003];
int dfs(int pos,int tleft){
if( mem[pos][tleft] != -1 ) return mem[pos][tleft];
if(pos == n+1)
return mem[pos][tleft] = 0;
int dfs1,dfs2 = -INF;
dfs1 = dfs(pos+1,tleft);
if( tleft >= tcost[pos] )
dfs2 = dfs(pos+1,tleft-tcost[pos]) + mget[pos];
return mem[pos][tleft] = max(dfs1,dfs2);
}
int main(){
memset(mem,-1,sizeof(mem));
cin >> t >> n;
for(int i = 1;i <= n;i++)
cin >> tcost[i] >> mget[i];
cout << dfs(1,t) << endl;
return 0;
}
```
此时 mem 的意义与 dfs 相同:
**在时间 tleft 内采集 后 pos 个草药, 能获得的最大收益**
这能 ac?
当然能. 这就是 "采药" 那题的 AC 代码~~(毕竟数据较弱,你懂得)~~
~~不过,本题正解是01背包~~
好了我们终于搞出了记忆化搜索
总结一下记忆化搜索是啥:
>不依赖任何 外部变量
>答案以返回值的形式存在, 而不能以参数的形式存在(就是不能将 dfs 定义成 dfs(pos,tleft,nowans) , 这里面的 nowans 不符合要求).
>对于相同一组参数, dfs 返回值总是相同的
## 记忆化搜索与动态规划的关系:(分析
基本是好朋~~(基)~~友关系
其实说白了,记忆化搜索就是dp
不信你看 mem 的意义:
>在时间 tleft 内采集 后 pos 个草药, 能获得的最大收益
这不就是dp的状态?
由上面的代码中可以看出:
dfs(pos,left)=max(dfs(pos+1,tleft−tcost[pos])+mget[pos] ,
dfs(pos+1,tleft))
即为
mem[pos][tleft]=max(mem[pos+1][tleft−tcost[pos]]+mget[pos] , mem[pos+1][tleft])
这不就是dp的状态转移?
总结一下:
记忆化搜索和动态规划从根本上来讲就是一个东西,(印象中)任何一个 dp 方程都能转为记忆化搜索 ,反之亦然
因为:
根据记忆化搜索的参数可以直接得到dp的状态,反之亦然
根据记忆化搜索的递归关系可以写出状态转移方程,这个方程可以直接写出循环式的dp,只不过是反的(想想为什么?),反之亦然
大部分记忆化搜索时空复杂度与 不加优化的 dp 完全相同
最重要的一点:二者思想类似!!
核心思想均为:利用对于相同参数答案相同的特性,对于相同的参数(循环式的dp体现为数组下标),记录其答案,免去重复计算,从而起到优化时间复杂度的作用。这,便是二者的精髓。
建议好好想想第四条。记住,**学一个算法,一定要理解他的精髓**。
举个栗子:
dp[i][j][k]=dp[i+1][j+1][k−a[j]]+dp[i+1][j][k]
转为
```cpp
int dfs( int i , int j , int k ){
边界条件
if( mem[i][j][k] != -1 ) return mem[i][j][k];
return mem[i][j][k] = dfs(i+1,j+1,k-a[j]) + dfs(i+1,j,k);
}
int main(){
memset(mem,-1,sizeof(mem));
读入
cout << dfs(1,0,0) << endl;
}
```
二者满足上面提到的所有关系
## 如何写记忆化搜索
方法I(由动态规划开始思考):
把这道题的dp状态和方程写出来
根据他们写出dfs函数
添加记忆化数组
举例:
dp[i]=max{dp[j]+1}1≤j<i且a[j]<a[i] (最长上升子序列)
转为
```cpp
int dfs( int i ){
if( mem[i] != -1 ) return mem[i];
int ret = 1;
for( int j = 1 ; j < i ; j++ )
if( a[j] < a[i] )
ret = max(ret,dfs(j)+1);
return mem[i] = ret;
}
int main(){
memset(mem,-1,sizeof(mem));
读入
cout << dfs(n) << endl;
}
```
方法II(由暴搜开始思考):
写出这道题的暴搜程序(最好是dfs)
将这个dfs改成"无需外部变量"的dfs
添加记忆化数组
举例: 本文最开始介绍"什么是记忆化搜索"时举的"采药"那题的例子,就是典型的方法II
## 记忆化搜索的优缺点
优点:
>记忆化搜索可以避免搜到无用状态, 特别是在有状态压缩时
举例: 给你一个有向图(注意不是完全图),经过每条边都有花费,求从点1出发,经过每个点**恰好一次**后的最小花费(最后不用回到起点),保证路径存在.
dp状态很显然:
设 dp[pos][mask] 表示身处在 pos 处,走过 mask (mask为一个二进制数) 中的顶点后的最小花费
常规 dp 的状态为 O(n⋅2n) , 转移复杂度(所有的加在一起)为 O(m)
但是!
如果我们用记忆化搜索,就可以避免到很多无用的状态,比如 pos 为起点却已经经过了 >1 个点的情况.
然后就 rk1 了
>不需要注意转移顺序(这里的"转移顺序"指正常dp中for循环的嵌套顺序以及循环变量是递增还是递减)
举例: 用常规 dp 写"合并石子"需要先枚举区间长度然后枚举起点,但记忆化搜索直接枚举断点(就是枚举当前区间由哪两个区间合并而成)然后递归下去就行
>边界情况非常好处理, 且能有效防止数组访问越界
>写起来简单易懂 至少我这么认为
>有些 dp(如区间 dp)用记忆化搜索写很简单但正常 dp 很难
>记忆化搜索天生携带搜索天赋,可以使用技能"剪枝"!
缺点:
>有些优化比较难加
>由于递归, 有时效率较低但不至于 TLE (状压dp除外)~~(so,dp万岁)~~
>代码有点长~~其实也不算太长~~
## 记忆化搜索的注意事项
千万别忘了加记忆化! (别笑, 认真的
边界条件要加在检查当前数组值是否为 - 1 前(防止越界)
数组不要开小了(逃
在某些时候需要优化(如滚动数组、斜率优化时还是要用正常的dp