网络流
jingyu0929
·
·
个人记录
基本概念
流网络
一个有向图,有一个源点( s )和一个汇点( t ),然后每一条边有一个容量( C(u,v) ),就差不多下面这个图,然后这里是不需要考虑反向边的。
然后这里的整个图包括点集和边集,写作 G = (V,E) ,显而易见这里的 V 就是点集, E 就是边集
可行流
这里的流量用 f(u,v) 表示,然后这里也是不用考虑反向边的捏,整个可行流用 f 表示,可行流有两个条件:
-
容量限制,也就是说这一条边里面流过的流量不能超过这个边的容量
-
流量守恒:网络流的点是不能存流量的,所以对于每一个点来说,都存在着流入的量等于流出的量
用式子来表示就是:
\forall $ $ u ,v\in V $ $ f(u,v) \leq C(u,v)
\forall $ $ u \in V $ , $ \sum f(u,v) = \sum f(v,u)
这个可行流的流量指从源点流出的流量减流入源点的流量, |f| = \sum f(s,v) - \sum f(v,s)
而最大流指的就是所有可行流里面流量最大的,下面就是一个可行流(好像是最大流(?),还有就是最大流不止一个捏)
残留网络
这里需要开始考虑反向边了捏。残留网络是对应原图的可行流来说的,每一个可行流都对应着一个残留网络,而残留网络中的点集 V' 和原来的流网络是一样的,边集就是原来的边集和原来边集的反向边的并集,简单理解就是原网络 - 可行流
然后残留网络每一个边对应的容量是这样的:
f'(u,v) = \begin{cases} c(u,v) - f(u,v) & \text{if } (u,v) \in E \\f(v,u) & \text{if} (v,u)\in E \end{cases}
然后有一个结论就是残留网络的可行流 f' + 原图对应的可行流 f = 原图另一个可行流,然后这个就是上面那个可行流的残留网络
增广路径
增广路径的意思就比较简单,就是在残留网络里面,从源点出发,经过的边边权都大于 0 ,到达汇点的路径叫做增广路径
因为由上面的残留网络的结论和增广路径的定义显然可以得到:如果一个可行流有增广路径,那么他就不是最大流,而且他的增广路径与可行流相加,所得到的可行流流量更大;反之,如果它没有增广路径,那他就是最大流,正确性显然。
所以就引出了求最大流的方法,先确定一个可行流,然后找到他的残留网络,然后看他有没有增广路径,如果有就和之前的可行流相加,再以此往复(如果错了就当这段狗叫捏)
割
一个流网络的割,就是两个点集,然后满足并起来就是 E ,交集是 ∅ ,并且源点和汇点分别在这两个集合当中。
=> S 和 T 集合, S ∪ T = E , S ∩ T = \emptyset
- 割的容量 : c(S,T) = \sum _{u ∈ S}^{v ∈T} c(u,v)
- 割的流量 : f(S,T) = \sum_{u \in S} ^ {v \in T} f(u,v) - \sum_{u \in S}^{v \in T} f(v,u)
-
\forall $ 可行流 $ f,\forall [S,T],|f| = f(S,T) \le c(S,T)
割的容量和割的流量是不对称的
最小割指的就是容量最小的割,而由上面的式子可以得到最大流的流量是小于等于最小割的容量的
最大流最小割定理
最大流核心概念捏
内容(以下三个点是等价的,可以互推的):
- 可行流 f 是最大流
- 可行流 f 的残留网络中不存在增广路径
- 对于可行流 f 来说,存在某个割 [S,T] 使得 |f| = c(S,T)
证明:① <-> ② 显而易见。③ - > ①,由割的公式可以知道, |最大流 f | \leq c(S,T) ,所以可以得到 |f| = c(S,T) \le |最大流|。② -> ③,首先定义以下 S 为在残留网络中从 s 出发沿容量大于 0 的边走,所有能到达的边, T = V- S ,显而易见的是, \forall u \in S,v \in T,f(u,v) = c(u,v) ,而 f(v,u) = 0 ,所以这个时候 |f| = c(S,T) ,因而②可以推③,所以上面三个点是可以互推的捏。
最大流算法
最大流算法一般维护的是残留网络,所以建的是双向边,用领接表存比较好找到反向边
EK
思路:找一个可行流,然后不断找他的残留网络有没有增广路径(用 bfs 找),如果有的话就更新残留网络,然后再次寻找;没有的话那么这个可行流就是最大流。
时间复杂度: O(nm^2) (指极限,一般时间复杂度的上界都是非常宽松的(y总锐评:最大流算法的时间复杂度其实就是根本就不用管,就是放屁啊),一般处理1e3 ~ 1e4的网络都可以滴)
存图:领接表,从 0 开始存,然后正反边连续存,成对存储正向边和反向边,这样找反向边就直接 ^ 1就可以了 。 Dinic 也是这样存图的
模板:
void add(int a,int b,int w) {
e[idx] = b, f[idx] = w,ne[idx] = h[a], h[a] = idx ++;
e[idx] = a, f[idx] = 0,ne[idx] = h[b], h[b] = idx ++;
}
bool bfs() {
memset(flag,0,sizeof flag);
int hh = 0,tt = 0;
q[0] = S;
flag[S] = true,d[S] = inf;
while (hh <= tt) {
auto u = q[hh ++];
for (int i = h[u]; ~i; i = ne[i]) {
int v = e[i];
if (!flag[v] && f[i]) {
flag[v] = true;
d[v] = min(d[u],f[i]);
pre[v] = i;
if (v == T)
return true;
q[++ tt] = v;
}
}
}
return false;
}
int EK() {
int ans = 0;
while (bfs()) {
ans += d[T];
for (int i = T; i != S; i = e[pre[i] ^ 1]) {
f[pre[i]] -= d[T];
f[pre[i] ^ 1] += d[T];
}
}
return ans;
}
Dinic
思路:和 EK 一样的就不写了,不一样的就是在每次宽搜的时候不是只找一条增广路径,而是每次在增广残留网络的时候,会先 bfs 一遍,建立分层图,然后在分层图上通过 dfs 的方式,把所有能够增广的路径全部找出来,然后增广。
时间复杂度: O(n^2m) ,比 EK 快,可以处理 1e4 - 1e5 。因为时间复杂度比较玄学,所以优化很重要捏。(y总再次锐评:网络流的时间复杂度不用管啊,网络流的时间复杂度就是一个笑话)
三大优化:
- 当前弧优化
- flow < limit
- 删点
void add(int a,int b,int w){
e[idx] = b,f[idx] = w,ne[idx] = h[a],h[a] = idx ++;
e[idx] = a,f[idx] = 0,ne[idx] = h[b],h[b] = idx ++;
}
int dfs(int u,int limit) {
if (u == T) return limit;
int flow = 0;
for (int i = cur[u]; ~i && flow < limit; i = ne[i]) {
cur[u] = i;//当前弧优化
int v = e[i];
if (de[v] == de[u] + 1 && f[i]) {
int t = dfs(v,min(f[i],limit - flow));
if (!t) de[v] = -1;//删点
f[i] -= t,f[i ^ 1] += t;
flow += t;
}
}
return flow;
}
bool bfs() {
queue<int> q;
q.push(S);
memset(de,-1,sizeof de);
de[S] = 0,cur[S] = h[S];
while (q.size()) {
auto u = q.front();
q.pop();
for (int i = h[u]; ~i; i = ne[i]) {
int v = e[i];
if (de[v] == -1 && f[i]) {
de[v] = de[u] + 1;
cur[v] = h[v];
if (v == T) return true;
q.push(v);
}
}
}
return false;
}
int dinic() {
int ans = 0,flow;
while (bfs()) {
while (flow = dfs(S,inf),flow) {
ans += flow;
}
}
return ans;
}
ISAP
然后这里的一个 $ gap $ 优化,在下面代码里面看就可以了()。ISAP的核心也在下面的代码里写了捏(
时间复杂度: $ O(mn^2)
void bfs() {
queue<int> q;
for (int i = 1; i <= n; i ++) {
de[i] = n;
}
q.push(T);//从汇点开始反向BFS,汇点加入队列
de[T] = 0;
while (q.size()) {
auto u = q.front();
q.pop();
for (int i = h[u]; ~ i; i = ne[i]) {
int v = e[i];
if (de[v] == n && f[i ^ 1]) {
//因为bfs用的反向边,容量为0,因此要判断正向边容量是否大于0
de[v] = de[u] + 1;//记录当前点的层次
siz[de[v]] ++;//统计每个层次有几个点
q.push(v);
}
}
}
}
int dfs(int u,int limit) {
if (u == T) {
return limit;
}
int flow = 0;
for (int i = h[u]; ~ i; i = ne[i]) {
int v = e[i];
if (de[u] == de[v] + 1 && f[i]) {//如果这条边的残量大于0,且没有断层
int t = dfs(v,min(f[i],limit - flow));
if (t) {
f[i] -= t;
f[i ^ 1] += t;
flow += t;
}
if (flow == limit) return flow;
}
}
//GAP优化,出现断层,无法到达t了
//为了与下一层分隔开,避免下次还会遍历到下一层
if (-- siz[de[u]] == 0)
de[S] = n + 1;
//Isap核心,到这里,说明入流量有富余,出流量都用完了,提升高度
de[u] ++;//层++
siz[de[u]] ++;//层数对应个数++
return flow;
}
int isap() {
int ans = 0;
bfs();//bfs一次,建立分层图
while (de[S] < n) {
ans += dfs(S,inf);
}
return ans;
}
HLPP
预流推进,主要思想就是:能推流就推流,往大了流,最后看看 T 有多少水,就是最大流
具体过程:
- 先从 S 点想周围点推流,然后把周围有余流的点入队( S 和 T 在 HLPP 里面都是不入队的)
- 不断的取队头元素(这里是优先队列,按照深度排序的那种,也就是取出高度最高的点),然后向周围点推流
- 若推完之后还有余流,更新高度标号,重新放入优先队列
- 队列空了的话就返回
但是这就有一个问题,会出现两个点不停地反复推的结果,所以就给每一个点一个高度,让水只能从高处往低出流,而在算法运行的时候,不断地让有余流的点更改高度,直到这些点全部都没有余流。
为什么这样就没有来回推的情况了呢,=>当两个点在来回推流的时候,它们的点会不断上升,当他们的高度大于 S 的时候,就会把余流退给 S
所以在算法开始之前,要先把 S 的高度设为 n ,免得一开始 S 周围的那些点就把流还给 S 了。
```cpp
struct cmp {
//优先队列中按照深度排序
bool operator () (int a,int b) const {
return de[a] < de[b];
}
};
priority_queue<int,vector<int>,cmp> q;
il void pushflow(int u) {
for (int i = h[u]; ~ i; i = ne[i]) {
int v = e[i];
if (f[i] && de[u] == de[v] + 1) {
int t = min(f[i],flow[u]);
flow[u] -= t,flow[v] += t;
f[i] -= t,f[i ^ 1] += t;
if (v != S && v != T && !flag[v]) {
q.push(v);
flag[v] = true;
}
if (!flow[u]) break;
//如果流量已经用完了,提前返回
}
}
}
il void relabel(int u) {
//把u的高度更改为与u相邻的最低的而且还有容量的点的高度 + 1
de[u] = inf;
for (int i = h[u]; ~ i; i = ne[i]) {
int v = e[i];
if (f[i] && de[u] > de[v] + 1)
de[u] = de[v] + 1;
}
}
int que[N];
//建立分层图,从汇点开始
il void bfs() {
int hh = 0,tt = 0;
que[0] = T;
memset(de,-1,sizeof de);
de[T] = 0;
while (hh <= tt) {
int u = que[hh ++];
for (int i = h[u]; ~ i; i = ne[i]) {
int v = e[i];
if (de[v] == -1 && f[i ^ 1]) {
de[v] = de[u] + 1;//记录当前点的层次
que[++ tt] = v;
}
}
}
}
//最大标号预流推进算法
il lwl hlpp() {
bfs();
//如果S和T不连通的话,直接返回-1
if (de[S] == -1)
return 0;
de[S] = n;//设置S的高度为n,避免周围点一开始就把流量还回来了
//统计每一个深度点的数量
for (int i = 1; i <= n; i ++) {
if (de[i] > -1)
siz[de[i]] ++;
}
//从源点预流推进,因为源点不加入队列,就再外面跑了
for (int i = h[S]; ~ i; i = ne[i]) {
int v = e[i],w = f[i];
if (w) {
//一开始把周围的点都堆满流,后续如果多了(有余流),再还回来
flow[S] -= w,flow[v] += w;
f[i] -= w,f[i ^ 1] += w;
if (v != S && v != T && !flag[v])
q.push(v);
}
}
//不断从优先队列取高度最高的点进行推流
while (q.size()) {
auto u = q.top();
q.pop();
flag[u] = false;
pushflow(u);//对u点进行推流
//如果还有余流的话,要往回退流了,提升高度
if (flow[u]) {
siz[de[u]] --;
//断层了,GAP优化
if (! siz[de[u]]) {
for (int i = 1; i <= n; ++ i) {
if (i != T && i != S && de[i] > de[u]) {
de[i] = n + 1;
//标记为无法到达
}
}
}
relabel(u);
//HLPP的特别标记规则,ISAP是直接加加
siz[de[u]] ++;
q.push(u);
flag[u] = true;
}
}
return flow[T];
}
```
## 有上下界的网络流
整一个wanqitzh的手绘图()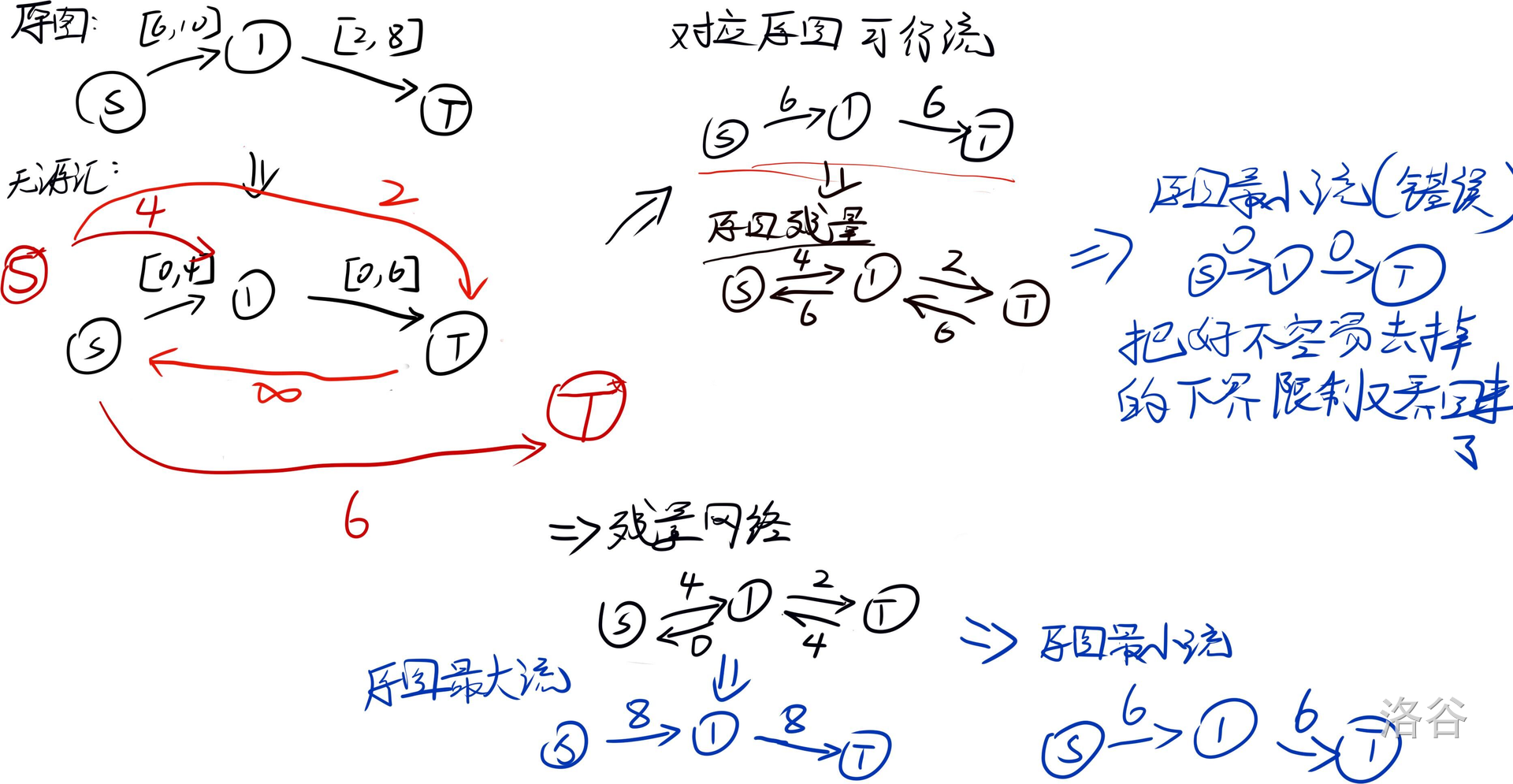
### 无源汇上下界可行流
建一个虚拟源点和虚拟汇点,然后在连边的时候所有边的容量都减去下界,接下来算一下每一个点的出入,如果入和出不一样,就向源点或者汇点连边,如果源点的出边和(也就是 $ dinic $ 求出来的最大值和之前求的所有多的入的和是一样的,那就说明有解)
然后如果有解的话,每一条边的流量再加上原来的下届就是现在这条边的流量,输出就可以了(),然后就是因为这里 $ f $ 数组存的是残留网络,所以在输出的时候要用 $ f[i $^$ 1] $ 加上下界。
```cpp
void add(int a,int b,int up,int down) {
e[idx] = b,f[idx] = up - down;
l[idx] = down,ne[idx] = h[a],h[a] = idx ++;
e[idx] = a,f[idx] = 0,ne[idx] = h[b],h[b] = idx ++;
}
S = 0,T = n + 1;
memset(h,-1,sizeof h);
int a,b,c,d;
for (int i = 1; i <= m; i ++) {
a = fr(),b = fr(),d = fr(),c = fr();
add(a,b,c,d);
w[a] -= d,w[b] += d;
}
for (int i = 1; i <= n; i ++) {
if (w[i] > 0) {
sum += w[i];
add(S,i,w[i],0);
} else if (w[i] < 0) {
add(i,T,-w[i],0);
}
}
int ans = dinic();
if (ans != sum) {
wj;
return 0;
} else {
puts("YES");
for (int i = 0; i < m * 2; i += 2) {
fw(f[i ^ 1] + l[i]);
ch;
}
}
```
### 有源汇上下界
这里有最大流和最小流两种,但是因为他们的代码和思路其实都差不多,所以就放一起了。
有源汇的其实建边还有判断有没有解和无源汇是一样的(显而易见),唯一不一样的就是在所有边都建完之后要从 $ t $ 到 $ s $ 连一条 $ inf $ 的边,这是因为后面算流的时候 $ s $ 和 $ t $ 的流量是可以不守恒的( $ s $ 的出可以多, $ t $ 的入可以少)。
接下来因为跑了一遍 $ dinic $ ,所以现在 $ idx - 1 $ 这条边的流量对应的就是现在这个可行流的流量,用一个数记录下来。接下来还要把附加边去掉跑 $ dinic $ ,所以现在需要把附加边去掉。去掉这个比较简单,就是把 $ s $ 和 $ t $ 之间连的那条边去掉就可以了,去掉之后就算从 $ s $ 跑到了 $ S $ ,也不会接着往后面扩展了(因为现在从 $ S $ 往外面连的边都是满流量的,所以从 $ S $ 出去的残留网络 $ f $ 都是 $ 0 $ )
- 再然后,如果是在求最大流的话,就从 $ s $ 往 $ t $ 跑一遍 $ dinic $ ,然后用之前记录的 $ f[idx] $ 加上现在求出来的流量就是最大流。
- 如果求的是最小流的话,就从 $ t $ 往 $ s $ 跑一遍 $ dinic $ ,然后用之前记录的减去现在求的这个就是最大流,其实就是相当于从 $ t $ 往前面找最多可以退回去多少流量
*代码*,就贴一个最小流的,最大流的都差不多
```cpp
S = 0,T = n + 1;
for (int i = 1; i <= m; i ++) {
a = fr(), b = fr(),down = fr(),up = fr();
add(a,b,up - down);
w[a] -= down,w[b] += down;
}
for (int i = 1; i <= n; i ++) {
if (w[i] > 0) {
sum += w[i];
add(S,i,w[i]);
} else if (w[i] < 0) {
add(i,T,-w[i]);
}
}
add(t,s,inf);
int ans = dinic();
if (ans < sum) {
wj;
return 0;
} else {
S = s,T = t;
ans = f[idx - 1];
f[idx - 1] = 0,f[idx - 2] = 0;
//删掉所有附加边
int res = dinic();
fw(ans + res);
}
```
## 拆点
这是一种网络流常用的(常用吧,应该吧)的方法,就是当一个点他有流过的最大限制的时候,一般是把这个点拆成两个点,然后所有进入这个点的流量连到其中一个点上面,出去这个点的流量连到另外一个点上面去,然后再在这两个点之间连一条容量为这个点流量限制的边。
我看y总的代码一般用的是 $ + n $ ,但是我就喜欢直接乘二和乘二减一,应该都没有关系。
然后拆点的时候要注意的地方就是,开点的数量要开两倍,而且要分清楚哪个是入的点,哪个是出的点,在这两个点之间连边的时候是从入的点连到出的点
连边的代码比较短捏,这是餐饮这道题拆点和连边的一部分代码,主要就是贴贴拆点()
```cpp
for (int i = 1; i <= n; i ++) {
c = fr(),d = fr();
add(i * 2,i * 2 - 1,1);
for (int j = 1; j <= c; j ++) {
a = fr();
add(N - 5 - a - D,i * 2,1);
}
for (int j = 1; j <= d; j ++) {
b = fr();
add(i * 2 - 1,N - 5 - b,1);
}
}
```
# 最小割
前面写过最小割的基本定义了,其实单纯求最小割就是直接跑一遍最大流就可以了,这两个值都是一样的。但是只是最大流流量 = 最小割容量,但是残留网络里面流量为 $0$ 的边不一定是割边捏
一般最小割会用在每个点二者选其一或者最大权闭合子图这种题目。
## 求最小割的方案
直接 $ dfs $ 就可以了,弄一个标记数组 $ flag $ 然后从源点开始 $ dfs $ ,每次走残余流量大于 $ 0 $ 的边,也就是说跟 $S$ 相连的点,然后把那个点标记上(标记了的点就是在 $ S $ 集合的点)
比较简单,也很好懂,*代码*
```cpp
void get(int u) {
flag[u] = true;
for (int i = h[u]; ~ i; i = ne[i]) {
int v = e[i];
if (!flag[v] && f[i] > 0) {
get(v);
}
}
}
```
## 二者选其一
> $ eg $ . 有 $ n $ 个物品和两个集合 $ A $ , $ B $ ,如果一个物品没有放入 $ A $ 集合会花费 $ w_{1i} $ ,如果一个物品没有放入 $ B $ 集合会花费 $ w_{2i} $ ,如果两个物品不在一个集合会花费 $ val_i $ ,求最小花费
这种题就是经典的 **二者选其一** 的最小割问题。这个题的连边方式是将集合 $ A $ 和 $ B $ 设为源点和汇点,然后根据每一个要求连边。例如上面一种题目,对于 $ w_{1i} $ 这个花费,就向源点连一条权值为 $ w_{1i} $ 的边,然后对于 $ w_{2i} $ 也是差不多的连法。而对于每一个 $ val_i $ ,就在 $ u $ 和 $ v $ 之间连一条容量为 $ val_i $ 的双向边就可以了,然后这样跑出来的最小割( $ dinic $ )就是最小花费了。
二者选其一例题 [here](https://www.luogu.com.cn/problem/P1361)
## 最大权闭合子图
> $ eg $ .给定一张有向图,每个点都有一个权值,需要找出一个权值和最大的子图,使每个点的后继都在子图中,求权值和最大为多少
做法 :建立超级源点 $ S $ 和超级汇点 $ T $ ,如果节点 $ u $ 的权值为正,就从 $ S $ 连一条边,如果权值为负,就向 $ T $ 连一条边。然后把所有正点权都加到 $ sum $ 里面去,然后对于原图中的每一条边都连上,然后把容量设置为 $ inf $ 。然后跑一个最小割,最后用 $ sum $ 减去跑出来的答案就是要求的最大权值和
最大权闭合子图例题 [here](https://www.luogu.com.cn/problem/P4174)
### 证明
1. 每一个符合条件的子图都对应着流量网络中的一个割。因为每一个割将网络分为两个部分,与 $ S $ 相连的点满足没有边指向另一部分,男足条件
2. 最小割所去除的边必须与 $ S $ 或者 $ T $ 相连,也就是说不会去掉原图中的边。因为原图中的边连的边权是 $ inf $ ,如果去掉了就不是最小割了。
3. 选择的那部分子图的权值和是所有正权值之和 - 没有选择的正权点权值之和 - 选择的负权值(此处是绝对值)之和(显而易见)。而当我们不选择一个正权点的时候,在最小割中的体现就是断掉它和 $ S $ 之间的边;当我们选择一个负权边的时候,它和 $ T $ 的连边就会被断掉。也就是说我们求出的最小割就是(没有选择的正权点权值和 + 选择的负权点权值之和),所以就可以把上面的权值和转化成
> **最大权值和 = 所有正权值之和 - 最小割**
## 其它的一些
### 平面图和对偶图
平面图定义:如果 $ G $ 的任何两条边都没有除了顶点外的交点,那就是平面图(在 $ oiwiki $ 上是:{如果图 $ G $ 能画在平面 $ S $ 上,即除了顶点外无边相交,则称 $ G $ 可平面嵌入 $ S $ , $ G $ 为可平面图或平面图。画出的没有边相交的图称为 $ G $ 的平面表示或者平面嵌入。},但是以我现在的理解能力还看不懂,所以先放着)
然后下面的 $ G $ 都是一个平面图
面:由 $ G $ 的边将 $ G $ 所在的平面划分成若干个区域,每个区域称为 $ G $ 的一个面。期中面积无限的面(不是被围起来的封闭图形)称为无限面或者外部面,面积有限的(封闭图形)称为有限面或者内部面。包围每个面的所有边组成的回路称为该面的边界,边界的长度称为该面的次数。
平面中所有面的次数之和等于原图边数的两倍(每个边都在两个面中,会算两次)
极大平面图 :若在 $ G $ 的任意不相邻顶点间添加边,所得的图为非平面图,那么 $ G $ 是极大平面图。若 $ G $ 为 $ n(n \ge 3) $ 阶的连通平面图,那么 $ G $ 为极大平面图当且仅当 $ G $ 的每个面的次数均为 $ 3 $ 。
对偶图 : $ G $ 为平面图的某一个平面嵌入,构造 $ G^* $ 。
1. 在 $ G $ 的每一个面 $ R_i $ 中放置 $ G^* $ 的一个顶点 $ {u_i}^*
- 设 e 为 G 的一条边,若 e 在 G 的面 R_i 和 R_j 的公共边界上,做 G^{* } 的边 e^{* } 与 e 相交,且 e^* 关联 G^{* } 的顶点 v_i^* , v_j^* ,即 e^* =(v_i^* , v_j^* ),e^* 不与其他任何边相交。若 e 为 G 中桥且在 R_i 的边界上,则 e^* 是以 R_i 中顶点 v_i^* 为端点的环,即 e^* = (v^{* }_i,v^{* }_j)
平面图转成对偶图之后,有一个性质:平面图最小割 = 对偶图最短路。例题 here
最大密度子图
给定无向图 G=(V,E) ,其子图记为 G^* =(V^* ,E^* ) ,在所有子图构成的集合中,密度 D=|E^* ||V^* | 最大的元素称为最大密度子图。
原理
首先先进行二分,二分出一个 g (密度),对于 max(|E ^ * | - g * |V ^ * |) ,如果它大于 0 ,那么说明答案更大,否则答案更小。
但是怎么求 max(|E ^ * | - g * |V ^ * |) 呢?先将它写成一个以 g 为自变量的函数 h(g) 。但是现在这个式子没有什么好求的性质,于是尝试向最小割转化。
首先令 cnt[V',\overline{V^* }] 表示 不在子图 G ^ * 内部边的个数, d[u] 表示点 u 的度数
对于 |E^* | ,有:
|E'| = \frac{\sum_{u\in V'}d_u - cnt[V',\overline{V'}]}{2}
也就是说对于 h(g) 来说,我们有
h(g) = \frac{1}{2}(\sum_{u\in V'}d_u - cnt[V',\overline{V'}]-2g|V'|)
而对于 2g|V'| = \sum_{u\in V'}2g ,我们有
h(g) = \frac{1}{2}(\sum_{u\in V'}{(d_u-2g)} - cnt[V',\overline{V'}])
因为要转化为最小割,所以要转化成最小化 - h(g)
-h(g) = \frac{1}{2}(\sum_{u\in V'}{(2g-d_u)} + cnt[V',\overline{V'}])
于是乎就这个样子建图:
- 原图中的边两个点之间连接容量为 1 的双向边。
-
- 源点 S 向点 u 连接一条容量为 U 的边
证明
对于一个割而言,容量满足:
c[s,t]=\sum_{u\in \overline{V'}}U + \sum_{u\in V'}(2g-d_u+U) + \sum_{u\in V'}\sum_{v\in \overline{V'}}c(u,v)
转化一下(把两个 U 都提出来, |V|'+|\overline{V'}| = |V| ):
c[s,t]=|V|U + \sum_{u\in V'}(2g-d_u) + \sum_{u\in V'}\sum_{v\in \overline{V'}}c(u,v)
而可以发现 :
\sum_{u\in V'}(-d_u) + \sum_{u\in V'}\sum_{v\in \overline{V'}}c(u,v) $ 恰好就是 $ -2|E'|
故而可以推得:
c[s,t]=|V|U + \sum_{u\in V'}(2g) - 2|E'|
整理一下得:
c[s,t]=|V|U + 2(g|V'| - |E'|)
这就意味着最小割对应着最小的 -h(g) = g|V'| - |E'| ,也就是最大的 h(g) = |E'| - g|V'| ,这样就解决了()
在具体实现的时候, U 是为了保证容量非负,所以 U = |E'| 就可以。
费用流
含义:所有最大可行流当中,费用的最大值和最小值。定义每一条的费用为 w(u,v) 。相当于每一个管道有一个运输成本(?)
可行流的费用: \sum_{u \in V}^{v \in V} f(u,v)* w(u,v)
如果 G 有最大流,它不一定可以把最小费用最大流求出来(是有的),就像下面这个图(黑色的是容量,蓝色的是费用):
求法:把之前的 EK 算法里面的 bfs 换成 spfa 就可以了。 spfa 里面的最短路径的标准按照费用来跑,也就是说这里的边权按照费用和流量的乘积跑,但是这里的 spfa 是没有办法处理有负环的图的。
然后显而易见的是,求最小费用就用最短路的板子,求最大费用就用最长路的板子
模板
具体的看上面的 EK 算法,这里就提个代码了捏。具体思路就是上面的 EK ,不知道这里能不能用 dij ,但是懒得写了。
然后这里 spfa 的清空要注意一下,本来所有 minf 都是要清空的,但是 spfa 跑完之后要的只有 minf[T] ,所以就不用全部清空,直接 min[T] = 0 就可以咯。然后好像 flag 可以清空也可以不清空,我写 spfa 习惯了把 flag 清空,所以就懒得改了,到时候如果被卡掉了再改吧
void add(int a,int b,int wf,int ww) {
e[idx] = b,f[idx] = wf,w[idx] = ww;
ne[idx] = h[a],h[a] = idx ++;
e[idx] = a,f[idx] = 0,w[idx] = -ww;
ne[idx] = h[b],h[b] = idx ++;
}
bool spfa() {
queue<int> q;
memset(flag,0,sizeof flag);
memset(dis,0x3f,sizeof dis);
minf[T] = 0;
q.push(S);
flag[S] = true,minf[S] = inf;
dis[S] = 0;
while (q.size()) {
auto u = q.front();
q.pop();
flag[u] = false;
for (int i = h[u]; ~i; i = ne[i]) {
int v = e[i];
if (f[i] && dis[v] > dis[u] + w[i]) {
dis[v] = dis[u] + w[i];
pre[v] = i;
minf[v] = min(minf[u],f[i]);
if (!flag[v]) {
flag[v] = true;
q.push(v);
}
}
}
}
return minf[T] > 0;
}
void EK() {
flow = 0,cost = 0;
while (spfa()) {
flow += minf[T];
cost += minf[T] * dis[T];
for (int i = T;i != S; i = e[pre[i] ^ 1]){
f[pre[i]] -= minf[T];
f[pre[i] ^ 1] += minf[T];
}
}
}