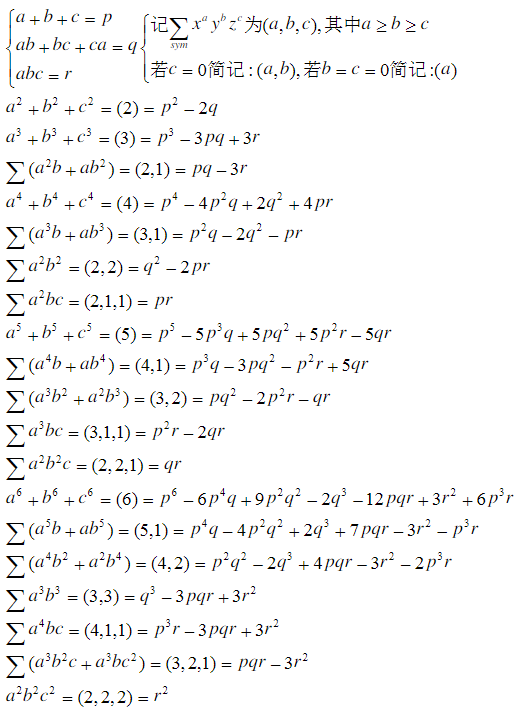不等式证明——pqr法学习笔记
18Michael
·
·
个人记录
前置知识:舒尔不等式。
对于每一个能取到的 $p$ 与 $q$,我们都可以把式子转化成关于 $r$ 的函数,当次数是 $4,5$ 次时可以看做是关于 $r$ 的一次函数,当次数是 $6,7,8$ 时可以看做是关于 $r$ 的二次函数,这样最值一定在$r$的最值时取到,我们只要讨论 $r$ 的最值即可。
1. 当三元不等式转化成关于 $r$ 的一次函数的时候,$r$ 的最值一定在原三数存在一数为 $0$ 或者两数相等的时候取到。([证明](https://wenku.baidu.com/view/f4a9da8da0116c175f0e4876.html))
2. 当三元不等式转化成关于 $r$ 的二次函数的时候,我们只需考虑此二次函数的开口和对称正负便可判断 $r$ 在何处取到最值。
下面是 $6$ 次和 $6$ 次以下对称式和 $pqr$ 之间的转化: