可能是废话最多的 FFT 教程
hanzhongtlx
·
·
个人记录
更好的阅读体验点这里
这是某不知名博主颓废之余的作品,篇幅可能很长,主要是力争自己以后忘了还可以看懂,也能引导其他读者(虽然可能没人看)不费脑子地看完(?)
引入
多项式是初中数学就接触的概念了,比如 F(x)=x^3+2x^2+8x-1 就是一个三次多项式,而我相信你对多项式的各种运算都了如指掌,今天我们就来探讨多项式乘法。
你说这不简单?比如 F(x)=x^2+2x+1 与 G(x)=2x+1 相乘,结果是 P(x)=2x^3+5x^2+4x+1,虽然没什么问题,但我们考虑一个 n 次多项式与 m 次多项式相乘,我们将每一项都相乘,运算的复杂度是 \mathcal O(nm) 级别的。
当我们遇到比较大的数据,比如 10^5 甚至更大时,那岂不是要谢?
能算就不错了,怎么事还这么多?
今天要引入的 FFT 就是来解决这个问题的。
多项式的表示方法
我们知道一个多项式 F(x) 可以表示为以下这种形式:
F(x)=\sum_{i=0}^n a_ix^i
我们称之为多项式的系数表示法。
那有没有其他表示方式呢?
想一想我们常做的数学题,一个二次函数,如果知道他经过的三个点,就可以用待定系数法求出其解析式。
同理,对于一个 n 次多项式,知道其经过的 n+1 个点,也可以求出其解析式,也就是说点足够多,多项式就唯一确定。
那么我们就可以得到多项式的点值表示法,即多项式 F(x) 经过的 n+1 个点 (x_i,y_i)(i\in [0,n]\cap\mathbb Z)。
一些相关概念
DFT(离散傅里叶变换):\mathcal O(n^2) 时间实现系数表示的多项式转换为点值表示的多项式的算法;
FFT(快速傅里叶变换):\mathcal O(n\log n) 时间实现系数表示的多项式转换为点值表示的多项式的算法;
IDFT(离散傅里叶逆变换):\mathcal O(n^2) 时间实现点值表示的多项式转换为系数表示的多项式的算法;
IFFT(快速傅里叶逆变换):\mathcal O(n\log n) 时间实现点值表示的多项式转换为系数表示的多项式的算法;
(tips:我们一般以 FFT 称 FFT 和 IFFT 的结合体,一方面是因为解决问题时这两者一般是分不开的且 FFT 比 IFFT 更为基本和重要,另一方面是因为 IFFT 的方法与 FFT 基本相同,因此以 FFT 称呼两者之和成为了一种惯称。)
NTT(快速数论变换):FFT 算法的改进和优化,不知道鸽到哪一天也写一写......
数学家神奇的脑回路
今天要引入的计算多项式的算法 FFT 的中心思想就是将系数表示的多项式转化为点值表示的多项式,计算乘法后再转换回去。
显然,这样看似唯一的优点就是计算多项式乘法时,复杂度是 \mathcal O(n) 的,因为只需要将横坐标相同的纵坐标相乘即可,我们只需要保证两个多项式带入的点的横坐标相同,在具体操作时,因为 F(x)\times G(x) 是 n+m 次的,所以我们 F(x) 与 G(x) 都需要带入至少 n+m+1 个点。
但是点值表示和系数表示的互相转化,也很让我们头疼,利用我们熟悉的秦九韶算法和拉格朗日插值法,仅仅能将复杂度维持在 \mathcal O(n^2),得不偿失,不禁让人有南辕北辙之感。
这就是数学家们不同寻常之处了,因为朴素的算法已经被玩透了,优化很难,这种清奇的思路涉足还少,或许奇迹正在其中。
(tips:下面我们先讨论将系数表示的多项式变为点值表示的多项式的方法,即 FFT 的方法。)
从分治思想开始的计划
不知哪一天,有人想到将 F(x) 按项的次数奇偶分治,比如对于多项式:
F(x)=5x^5+4x^4+3x^3+2x^2+x-1
有:
F(x)=(4x^4+2x^2-1)+(5x^5+3x^3+x)
对于奇数项,提出一个 x ,并令 y=x^2,有:
F(x)=(4y^2+2y-1)+x(5y^2+3y+1)
不妨设 A(x)=4x^2+2x-1、B(x)=5x^2+3x+1,这时:
F(x)=A(x^2)+xB(x^2)
这时候由于大部分函数都有自变量 x 的平方,使得带入一对相反数容易想到,比如带入 a 和 -a,有:
F(a)=A(a^2)+aB(a^2)
F(-a)=A(a^2)-aB(a^2)
容易发现基本是一样的数字,只是变了一下符号而已。
那么我们为何不递归下去,每次都分治,虽然具体操作和复杂度可能还是很懵,但是总归感觉好像确实有些用处?
我们不妨以七次多项式为例,不妨称递归到第 i 层生成的第 j 个函数为 F_{i,j}(x):
那么 F_{1,1}(x) 是七次多项式,需要带入 8 个点值;
$F_{3,i}(x)$ 是一次多项式,需要带入 $2$ 个点值(本层有四个多项式)($i\in [1,4]\cap\mathbb Z$);
$F_{4,i}(x)$ 是零次多项式(常值多项式),需要带入 $1$ 个点值(本层有八个多项式)($i\in [1,8]\cap\mathbb Z$)。
看起来没啥毛病,但是我们带入点值逐层减半的条件是上一层带入的数全是成对的相反数。
当然还需要保证每一次带入的点值都是 $2$ 的幂次,这样才能保证不断减半,当然这好维护,我们不必一定就带入 $n+1$ 个点值,而是带入不小于 $n+1$ 的最小 $2$ 的次幂个点值。
当然,为了在将点值转换为系数表示时为了能够有足够多的点,我们需要带入不小于 $n+m+1$ 的最小 $2$ 的次幂个点值。
这(指成对相反数这一条件)好像与我们每一层要计算的数是上一层数的平方向违背,既然是平方数,而且不都是零,怎么可能有产生成对的相反数?
是啊,除非......在复数领域。
### 复数的插手
你别说,复数,不是不能试,计算原理和实数毕竟一样啊。
什么是复数?
先定义复数单位 $i=\sqrt{-1}$,比如 $\sqrt{-4}=2i$,复数都可以写成 $a+bi$ 的形式($a$、$b\in\mathbb R$),其中 $a$ 为实部,$b$ 为虚部。
特殊地,实数可以看做虚部为 $0$ 的复数。
复数更神奇的是,他可以在平面直角坐标系上表示,这个坐标系横坐标单位长度为 $1$,纵坐标单位长度为 $i$,即 $a+bi$ 对应点 $(a,b)$,这个平面称为复平面。
复数的运算也较为简单,我们重点讲解加减法和乘法。
计算法则如下:
$$(a+bi)\pm(c+di)=(a\pm c)+(b\pm d)i$$
$$\left(\text{即实部和虚部分别相加减}\right)$$
$$\begin{aligned}(a+bi)(c+di)&=ac+bdi^2+adi+bci\\&=(ac-bd)+(ad+bc)i&(i^2=-1)\end{aligned}$$
另外我们规定复数的模长 $r=\sqrt{a^2+b^2}$,也就是复数对应的点在复平面到原点的距离。
我们不妨再讨论一下复数的几何意义,首先每一个复数 $z$ 都能写为这样的形式:
$$z=r(\cos(\theta)+i\sin(\theta))$$
其中我们将 $\theta$ 称为 $z$ 的辐角,一般的我们取 $\theta\in(0,2\pi]$,这时称 $\theta$ 为 $z$ 的辐角主值,记为 $\arg z$。
对于两个复数 $z_1=r_1(\cos(\theta_1)+i\sin(\theta_1))$ 和 $z_1=r_2(\cos(\theta_2)+i\sin(\theta_2))$ ,相乘的结果为:
$$z'=r_1r_2(\cos(\theta_1+\theta_2)+i\sin(\theta_1+\theta_2))$$
相关证明直接展开乘法运算即可,但我想强调的是复数乘法代表一个复数逆时针旋转另一个复数辐角主值的角度,模长变为两复数模长乘积。
即复数乘法的几何意义为复平面上旋转。
了解了复数的基本知识,我们是时候回过头想一想我们为什么要引入复数了。
对!我们要保证平方后任存在相反数。
我们不妨引入复数中最常用的一类数:单位根。
$n$ 次单位根即 $x^n=1$ 在复数域内的所有解,有 $n$ 个。
可是,为啥有 $n$ 个?
首先辐角主值为 $2\pi$ 的 $1$ 是一个可以瞪出来的解,其他的解我们可以联想复数的几何意义,我们在复平面内画单位圆,圆上的点对应的复数模长都是 $1$,取其中辐角主值为 $\dfrac{2\pi}{n}$ 的点对应的复数记为 $w_{n}$。
(tips:单位根最准确写法的应该是 $\omega_n^i$,这里为了书写方便,统一用 $w$ 代替 $\omega$,请见谅。)
由于乘法时旋转,$(w_n)^n$ 即从 $x$ 轴旋转了 $\dfrac{2\pi}{n}\times n$ 的角度,又回到了原点,即 $w_n^n=1$,同理 $w_n^k$ 也是相应的解,即:
$$\{1(w_{n}^0\text{或}w_n^n),w_n,w_n^2...w_n^{n-1}\}$$
被称为 $n$ 次单位根,根据复数的几何意义,不难知道(单位根的定义式):
$$w_{n}^k=\cos(\frac{2k\pi}{n})+i\sin(\frac{2k\pi}{n})$$
一个重要的性质是:
$$w_{n}^{k}=-w_{n}^{k+\frac{n}{2}}$$
其中负号代表实部和虚部全部取相反数,这条性质在几何意义和单位根的定义式中皆能体现。
对于例子来说:
不考虑乘法后点值表示法转换为系数表示法的过程,我们对于 $7$ 次多项式,只需要带入所有 $8$ 次单位根即可。
具体地,对于第一层的一个函数我们需要计算自变量取 $w_{8}^0\sim w_{8}^{7}$ 这 $8$ 个值时得到的函数值。
而正好又存在 $w_8^0$ 和 $w_{8}^4$、$w_{8}^1$ 和 $w_{8}^5$...... 这四对相反数,使得第二层的 $F_{2,1}(x)$ 和 $F_{2,2}(x)$ 只需要计算自变量为 $w_{8}^0,w_{8}^2,w_8^4,w_8^6$ 这四个值时的函数值,又存在两对相反数。
以此类推,第三层四个函数只需要计算自变量为 $w_8^0,w_8^4$ 时的函数值,第四层八个函数只需要计算自变量为 $w_8^0=1$ 时的函数值。
此时,皆已明朗,一共需要递归 $\mathcal O(\log n)$ 层,每一层虽然函数个数不同,需要带入的自变量个数不同,但乘积都是 $n+1$(准确来说是不小于 $n+1$ 的最小 $2$ 的幂次),而且层间函数值的传递都可以 $\mathcal O(1)$ 计算,即 FFT 的时间复杂度为 $\mathcal O(n\log n)$。
具体地,可以采用递归算法直接实现。
### 迭代 FFT
递归算法虽然较为易懂,但是其运行效率确实不敢恭维,我们急需将递归的过程利用直接顺推迭代的方法写出,从而达到优化的目的。
迭代的思路还是很清晰的,先粗略地盘算一下,我们将第 $i$ 层的第 $j$ 个函数值设为 $t_{i,j}$,递推关系式的寻找只是时间问题。
那我们先要找到对于每一层来说,这些函数值谁排在先,谁排在后的问题,即确定编号。
当然这个东西不能反人类,第一层不反人类的排法怕只有一种,就是:
(tips:仍以 $7$ 次多项式为例):
$$F_{1,1}(w_8^0),F_{1,1}(w_8^1),F_{1,1}(w_8^2)...F_{1,1}(w_8^7)$$
从前往后依次为 $t_{1,0},t_{1,1},t_{1,2}...t_{1,7}$。
对于最后一层,当然也只有一种不反人类的排法,即:
$$F_{4,1}(w_{8}^0),F_{4,2}(w_{8}^0),F_{4,3}(w_{8}^0)...F_{4,8}(w_{8}^0)$$
从前往后依次为 $t_{4,0},t_{4,1},t_{4,2}...t_{4,7}$。
当然,最后一层的 $8$ 个多项式函数都是常值函数,常值就是其对应的系数,因此 $t_{4,i}$ 的值只需要找到相应的第 $i$ 个位置系数就是得到。
我们不妨复盘一下分治的过程,引用一张图:
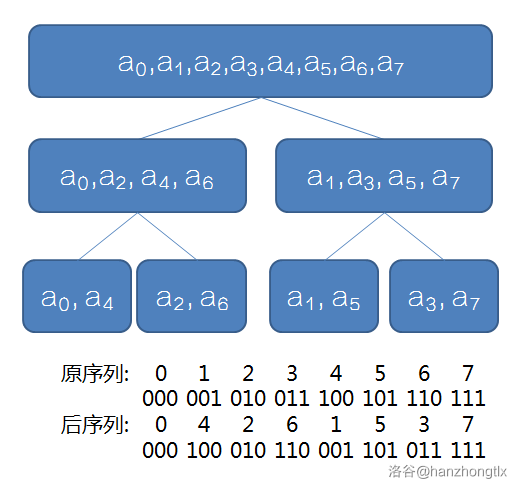
其中每一个方格都代表分治后,系数对应的项在一个函数里,注意没有画出最后一层。
不妨以 $F(x)=7x^7+6x^6+5x^5+4x^4+3x^3+2x^2+x-1$ 为例,其中令 $y=x^2$、$z=y^2=x^4$。
于是有:
$$\begin{aligned}F(x)&=7x^7+6x^6+5x^5+4x^4+3x^3+2x^2+x-1 \\&=(6y^3+4y^2+2y-1)+x(7y^3+5y^2+3y+1)\\&=[(4z-1)+y(6z+2)]+x[(5z+1)+y(7z+3)]\\&=[(-1+z\times4)+y(2+z\times6)]+x[(1+z\times5)+y(3+z\times7)]\end{aligned}$$
按之前的定义,比如 $F_{3,3}(x)=5x+1$、$F_{2,2}(x)=7x^3+5x^2+3x+1$......
递推的关系也有,比如:
$$F_{2,2}(x)=F_{_{3,3}}(x^2)+xF_{3,4}(x^2)$$
$$F_{2,2}(-x)=F_{_{3,3}}(x^2)-xF_{3,4}(x^2)$$
可以看到只要我们严格按照将偶数项放到前、奇数项放到后的原则,最后得到的最后一层的数字分别为:
$$a_0,a_4,a_2,a_6,a_1,a_5,a_3,a_7$$
这也是图中所揭示的,并且这些数字对应 $0,1,...7$ 这些数字的二进制反转。
也就是说我们只要求出 $0\sim 7$ 的二进制反转序列,将对应的数字赋值到 $t_{4,0}\sim t_{4,7}$,就能比较容易的递推了。
### 二进制反转序列的求解
我们虽然可以暴力记录每一位,然后暴力对应反转,但这还是慢了一些,我们可以借用递推的方式(dp),来解决问题。
考虑一个二进制串(位数足够且确定,比如对于 $0\sim 7$ ,只需要每个数 都使用 $3$ 位二进制就可以了),假如他有 $l$ 位,对应数字 $i$。
如果已知 $\left\lfloor\dfrac{i}{2}\right\rfloor$(相当于右移一位) 的二进制反转序列即 $i$ 二进制从前往后数前 $l-1$ 位的反转,那么其实只用将这 $l-1$ 位的反转放到二进制的 $2\sim l$ 位,再把原来的最后一位放到第一位就可以了,可以初始化 $0$ 的反转序列是 $0$,然后开始递推。
具体实现一行代码就够了:
```
for(int i=0;i<n;i++) res[i]=(res[i>>1]>>1)|((i&1)<<(l-1));//这样可以避免初始化,想想为什么
```
或运算前代表将前 $l-1$ 位放到后 $l-1$ 位,或运算后代表把最后一位放到反转序列的第一位,两部分之间也可以用加号连接。
### 空间的优化
我们按之前的思路来做,空间复杂度即 $t$ 数组的大小,可以知道是 $\mathcal O(n\log n)$,虽然还不错,但能不能更好?
容易想到一种滚动数组的方式,因为一层的更新只需要上一层的数据,这样空间复杂度就变为 $\mathcal O(n)$。
但好像又添加了一些繁琐的代码,有没有更好的方式?
关键就是选择一种合理的编号规则。
比较合理的有两种,我们不妨以 $7$ 次多项式的第三层为例,第一种是带入同一自变量的值放到一起,即:
$$F_{3,1}(w_8^0),F_{3,2}(w_8^0),F_{3,3}(w_8^0),F_{3,4}(w_8^0),F_{3,1}(w_{8}^4),F_{3,2}(w_{8}^4),F_{3,3}(w_{8}^4),F_{3,4}(w_{8}^4)$$
分别对应 $t_{3,0}\sim t_{3,7}$。
另一种是同一函数计算出的值放到一起,即:
$$F_{3,1}(w_8^0),F_{3,1}(w_{8}^4),F_{3,2}(w_8^0),F_{3,2}(w_{8}^4),F_{3,3}(w_8^0),F_{3,3}(w_{8}^4),F_{3,4}(w_8^0),F_{3,4}(w_{8}^4)$$
分别对应 $t_{3,0}\sim t_{3,7}$。
乍一看似乎都可以,但我们可以画个图,将递推关系画出来(纯手画,书写不是很好,勿喷 QWQ):
(tips:下图仅以 $2$、$3$ 层之间的递推为例):

可以看到~~卷面真的很烂~~第二种编号方式显然更加美观,因为对于一组相反数代入来说,对应的上一层的编号刚好与现在的编号对等,不像第一种一样如果直接更新就有可能影响后续更新。
换言之,对于第二种数组编号方式,我们只需要分别处理每组相反数代入的递归,这样修改数组,不会对其他的相反数对代入产生影响。
因此我们就可以在避免使用滚动数组的前提下做到 $\mathcal O(n)$ 的空间复杂度。
如果还是不明白,可以停下来品味一下。
### IFFT
依鄙人之见,IFFT 记住结论似乎就够用了(。
那么我们就先放结论,至于证明想看就看,不看就算了。
对于一个 $N+M$ 次多项式 $P(x)$(待求多项式),带入了 $w_{n}^0\sim w_{n}^{n-1}$(其中 $n$ 是不小于 $N+M+1$ 的最小的 $2$ 的幂次),得到的函数值为 $b_0\sim b_n$($b_n$ 是复数),那么 $P(x)$ 的系数 $a_{0}\sim a_{n}$(当然有可能 $a_n$ 啥的是 $0$ 但依然符合规律)符合:
$$a_k=\dfrac{1}{n}\sum_{i=0}^nb_iw_n^{-ki}\ \ \ \ \ (k\in[0,n]\cap\mathbb Z)$$
也就是说 $n a_k$ 是多项式 $Q(x)=\sum\limits_{i=0}^n b_ix^i$ 带入 $w_{n}^{-k}$ 后得到的函数值。
我们惊奇的发现这像极了 FFT 的过程,也是带入复数,这些负数也理所当然地满足不断折半并产生成对相反数的特质。
于是我们可以按照像 FFT 一样的方式去解决问题,只是换了带入的数而已。
另一方面 $w_n^k$ 和 $w_n^{-k}$ 其实只是 $1$ 在单位圆上分别向逆时针和顺时针方向旋转相同角度得到的,想象一下,其实只有纵坐标是相反的,即:
$$w_n^{-k}=\cos(\frac{2k\pi}{n})-i\sin(\frac{2k\pi}{n})$$
当然直接带到定义式中或许更有助于理解。
于是 FFT 的代码就可以写出了,具体解释可以看代码,如果再看不懂,可以翻翻前面,自己想想:
```
#include"iostream"
#include"cstdio"
#include"cmath"
using namespace std;
#define MAXN 1000005
int N,M,n=1,l;
int res[MAXN*3];
const double pi=acos(-1.0);
struct com
{
double x,y;
com(double xx=0,double yy=0){x=xx,y=yy;}
}w[MAXN*3],a[MAXN*3],b[MAXN*3];
//开3倍空间是因为N+M是2倍的,而不小于N+M+1的2的幂次很可能大于N+M的最大值
//但这个2的幂次(代码中为n)不会超过3倍的MAXN
com operator +(com a,com b){return com(a.x+b.x,a.y+b.y);}
com operator -(com a,com b){return com(a.x-b.x,a.y-b.y);}
com operator *(com a,com b){return com(a.x*b.x-a.y*b.y,a.x*b.y+a.y*b.x);}
//重载复数运算
void FFT(com *a,int unit)
{
w[0]=com(1,0),w[1]=com(cos(2.0*pi/n),unit*sin(2.0*pi/n));
for(int i=2;i<n;i++) w[i]=w[i-1]*w[1];
//预处理单位根,unit为1代表FFT,为-1代表IFFT,乘到虚部正好符合公式
for(int i=0;i<n;i++) if(i<res[i]) swap(a[i],a[res[i]]);
//i<res[i] 的特判是因为要避免一对二进制反转数被交换两次
//如果交换两次,结果和不交换一模一样
for(int i=2;i<=l+1;i++)//枚举层数
{
//这属于从最下面一层向上枚举,如i=2代表一次函数那一层
int t=n>>(i-1);//函数种类数
for(int j=1;j<=t;j++)//枚举函数
{
int s=n/t;//需带入的自变量的数量
for(int k=1;k<=(s>>1);k++)//枚举自变量
{
//因为成对处理,所以枚举一半
int op=s*(j-1)+k-1;
//函数个数等于角度单位倍数,因此对应w[(k-1)*t];
com g=w[(k-1)*t]*a[op+(s>>1)];
a[op+(s>>1)]=a[op]-g;
a[op]=a[op]+g;
//这里的编号是比较复杂度,建议看一看画出的编号示意图
}
}
}
}
int main()
{
scanf("%d%d",&N,&M);
for(int i=0;i<=N;i++) scanf("%lf",&a[i].x);
for(int i=0;i<=M;i++) scanf("%lf",&b[i].x);
while(n<=N+M) l++,n<<=1;
//寻找那个2的幂次
for(int i=0;i<n;i++) res[i]=(res[i>>1]>>1)|((i&1)<<(l-1));
FFT(a,1),FFT(b,1);
for(int i=0;i<n;i++) a[i]=a[i]*b[i];
//点值表示法意义下的乘法,直接对应相乘即可
FFT(a,-1);//IFFT
for(int i=0;i<=N+M;i++) printf("%d ",(int)(a[i].x/n+0.5));
//这里+0.5是保证精度的做法,而我们要输出的显然是实部
return puts(""),0;
}
```
### IFFT 结论的推导
我们首先知道 $b_i$ 得出的原理即:
$$b_k=\sum_{i=0}^n a_{i}w_{n}^{ki}$$
因此:
$$\begin{aligned}\sum_{i=0}^n b_iw_n^{-ki}&=\sum_{i=0}^n\sum_{j=0}^na_{j}w_{n}^{ij}\times w_n^{-ki}\\&=\sum_{j=0}^na_j\sum_{i=0}^nw_{n}^{i(j-k)}\end{aligned}$$
(tips:注意求和符号的交换是关键)
接下来我们稍微分一下类:
$1.$ 当 $j=k$ 时,有 $w_{n}^{i(j-k)}=w_{n}^0=1$,因此:
$$\sum_{i=0}^n w_n^{i(j-k)}=n\times 1=n$$
$2.$ 当 $j\not=k$ 时,我们利用等比数列求和公式可以得到:
$$\begin{aligned}\sum_{i=0}^n w_n^{i(j-k)}&=\frac{1\times\left(1-(w_n^{j-k})^n\right)}{1-w_n^{j-k}}\\&=\frac{1-w_n^{n(j-k)}}{1-w_n^{j-k}}\\&=\frac{1-(w_n^n)^{j-k}}{1-w_n^{j-k}}\\&=\frac{1-1^{j-k}}{1-w_n^{j-k}}\\&=0\end{aligned}$$
因此当且仅当 $j=k$ 时,$a_j$ 的因数才是 $n$ 而非零,因此:
$$\begin{aligned}\sum_{i=0}^n b_iw_n^{-ki}&=\sum_{i=0}^n\sum_{j=0}^na_{j}w_{n}^{ij}\times w_n^{-ki}\\&=\sum_{j=0}^na_j\sum_{i=0}^nw_{n}^{i(j-k)}\\&=a_k\times n\\&=na_k\end{aligned}$$
这样我们就证明了 IFFT 的合理性,当然这个推导过程其实就是大名鼎鼎的“单位根反演”。
### 常数上的优化
FFT 虽然实现了从递归到迭代的蜕变,但常数仍然不小,我们可以使用经典的“三次变两次”的方法优化常数。
原理就是完全平方公式:
$$\left(F(x)+iG(x)\right)^2=F^2(x)-G^2(x)+2iF(x)G(x)$$
因为我们其实本来就利用的是复数多项式,只是一开始让虚部都是 $0$,实际上确实造成了一定程度上的浪费,所以我们直接将 $F(x)+iG(x)$ 这个复数多项式平方,取虚部的一半就行了,因为 FFT 的过程只需要对一个多项式操作,所以常数就会小不少。
那这个算法是怎么想到的呢?
~~别问我啊,又不是我想到的~~,可能是为了减小 FFT 的操作次数好像也就只能想到平方了,~~所以就瞎构造了一通发现这个好像不错~~。
代码如下:
```
#include"iostream"
#include"cstdio"
#include"cmath"
using namespace std;
#define MAXN 1000005
int N,M,n=1,l;
int res[MAXN*3];
const double pi=acos(-1.0);
struct com
{
double x,y;
com(double xx=0,double yy=0){x=xx,y=yy;}
}w[MAXN*3],a[MAXN*3];
com operator +(com a,com b){return com(a.x+b.x,a.y+b.y);}
com operator -(com a,com b){return com(a.x-b.x,a.y-b.y);}
com operator *(com a,com b){return com(a.x*b.x-a.y*b.y,a.x*b.y+a.y*b.x);}
void FFT(com *a,int unit)
{
w[0]=com(1,0),w[1]=com(cos(2.0*pi/n),unit*sin(2.0*pi/n));
for(int i=2;i<n;i++) w[i]=w[i-1]*w[1];
for(int i=0;i<n;i++) if(i<res[i]) swap(a[i],a[res[i]]);
for(int i=2;i<=l+1;i++)
{
int t=n>>(i-1);
for(int j=1;j<=t;j++)
{
int s=n/t;
for(int k=1;k<=(s>>1);k++)
{
int op=s*(j-1)+k-1;
com g=w[(k-1)*t]*a[op+(s>>1)];
a[op+(s>>1)]=a[op]-g;
a[op]=a[op]+g;
}
}
}
}
int main()
{
scanf("%d%d",&N,&M);
for(int i=0;i<=N;i++) scanf("%lf",&a[i].x);
for(int i=0;i<=M;i++) scanf("%lf",&a[i].y);
while(n<=N+M) l++,n<<=1;
for(int i=0;i<n;i++) res[i]=(res[i>>1]>>1)|((i&1)<<(l-1));
FFT(a,1);
for(int i=0;i<n;i++) a[i]=a[i]*a[i];
FFT(a,-1),n*=2;
for(int i=0;i<=N+M;i++) printf("%d ",(int)(a[i].y/n+0.5));
return puts(""),0;
}
```
### 嘤用
FFT 最直接的应用就是计算两个多项式的乘积(即卷积),另外还可以用来优化高精度乘法。
你想啊,我们将一个高精度的数当做 $x$ 取 $10$ 时的多项式的值,因此我们可以先将多项式做乘法,然后再代入 $x=10$。
当然这样说可能抽象了一些,但是你想想你在列竖式时各个数位先乘后加的计算过程,不像极了多项式做乘法时不同项之间的运算吗?
### NTT
NTT 是对 FFT 的进一步优化,与 IFFT 相同,我还是倾向于记结论,不同的是我不会证明了(哭)。
在一般的多项式题目中,模数都是 $998244353$,而 $998244352=2^{23}\times7\times 17$。
只需记住 $p=998244353$ 的**原根** $g=3$,而
$$w_n\equiv g^{\frac{p-1}{n}}\pmod{p}$$
当然 $2^{23}$ 就已经是 $\mathcal O(n\log n)$ 能承受的极限了,所以指数位置是整数一般是不必担心的。
对于需要 $w_n^{-k}$ 的 IFFT,别忘了指数上负数代表倒数,这就好办了,$g=3$ 在模 $998244353$ 意义下为 $332748118$,用它代替就好了。
啥?你问这题都没叫取模为什么要用模数?因为我们操作中有逆元的引入,取模就不可避免了,代码和 FFT 基本一致,因为省去复数运算,所以常数会大大变小,但是这样就没有“三次变两次”的优化了。
代码如下:
```
#include"iostream"
#include"cstdio"
#include"cmath"
using namespace std;
#define MAXN 1000005
#define MOD 998244353
#define ll long long
int N,M,n=1,l;
int res[MAXN*3],w[MAXN*3],a[MAXN*3],b[MAXN*3];
int quickpow(int a,int b)
{
int ans=1,base=a;
while(b)
{
if(b&1) ans=(ll)ans*base%MOD;
base=(ll)base*base%MOD;
b>>=1;
}
return ans;
}
void NTT(int *a,int unit)
{
w[0]=1,w[1]=quickpow(unit,(MOD-1)/n);
for(int i=2;i<n;i++) w[i]=(ll)w[i-1]*w[1]%MOD;
for(int i=0;i<n;i++) if(i<res[i]) swap(a[i],a[res[i]]);
for(int i=2;i<=l+1;i++)
{
int t=n>>(i-1);
for(int j=1;j<=t;j++)
{
int s=n/t;
for(int k=0;k<(s>>1);k++)
{
int op=s*(j-1)+k;
int g=(ll)w[k*t]*a[op+(s>>1)]%MOD;
a[op+(s>>1)]=(a[op]-g+MOD)%MOD;
a[op]=(a[op]+g)%MOD;
}
}
}
}
int main()
{
scanf("%d%d",&N,&M);
for(int i=0;i<=N;i++) scanf("%d",&a[i]);
for(int i=0;i<=M;i++) scanf("%d",&b[i]);
while(n<=N+M) l++,n<<=1;
for(int i=0;i<n;i++) res[i]=(res[i>>1]>>1)|((i&1)<<(l-1));
NTT(a,3),NTT(b,3);
for(int i=0;i<n;i++) a[i]=(ll)a[i]*b[i]%MOD;
NTT(a,332748118);
int inv=quickpow(n,MOD-2);
for(int i=0;i<=N+M;i++) printf("%d ",(ll)a[i]*inv%MOD);
return puts(""),0;
}
```