Splay 学习笔记
Gokix
·
·
个人记录
前置知识:二叉查找树 BST。
满足对于每个节点,其左子树的所有结点都比自己小,右子树的所有节点都比自己大。
性质:树的中序遍历相当于把所有数从小到大排序。
模板:P5076 【深基16.例7】普通二叉树(简化版)
极端情况下,二叉查找树可能成为一条链。若每次都在链的最底端做操作,那时间复杂度就退化成暴力了。
所以我们需要平衡操作来使二叉查找树“平衡”,“平衡”的二叉查找树叫做平衡树。平衡的定义因平衡树而异,但总之不会让每一次查询的深度都特别低。
本 Blog 主要复习 Splay,即伸展树,由 Daniel Sleator 和 Robert Endre Tarjan 在 1985 年发明。
模板:P3369 【模板】普通平衡树
变量声明:
$f_u$:节点 $u$ 的父节点的编号。
$w_u$:节点 $u$ 的权值。
$s_u$:节点 $u$ 的子树大小(包括自己)。
$cnt_u$:权值为 $w_u$ 的数的个数。
$rt$:树根编号。
注意到 Splay 的儿子存储方式与一般的方法不同。这么存储的原因是它在判断父子的左右关系的时候可以省略大段的 if 判断,这一点可以在下面的讲解有很好的体现。
------------
下面开始函数的讲解:
1. chk(u):返回节点 u 是 f[u] 的左儿子(0)还是右儿子(1)
```cpp
bool chk(long long x){
return c[f[x]][1]==x;
}
```
这个感觉没有什么好讲的,自己手玩一下就好了。
`chk` 函数在之后会极大地使代码变得简洁。
------------
2. refresh(u):维护 s[u] 的大小
```cpp
void refresh(long long x){
s[x]=s[c[x][0]]+s[c[x][1]]+cnt[x];
}
```
这个感觉也没什么好讲的。
------------
3. rotate(u):单旋,u 代替 f[u] 的位置
```cpp
void rotate(long long x){
long long y=f[x],z=f[y],k=chk(x);
c[y][k]=c[x][k^1],f[c[x][k^1]]=y;
c[z][chk(y)]=x,f[x]=z;
c[x][k^1]=y,f[y]=x;
refresh(y),refresh(x);
}
```
Splay 重要操作之一。
我们先看这个两个图:
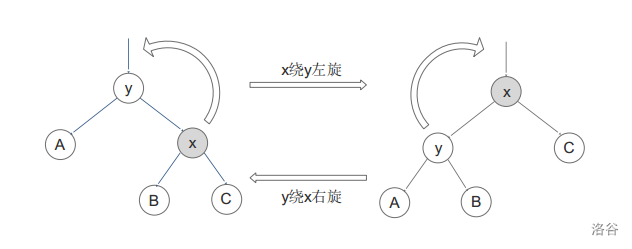
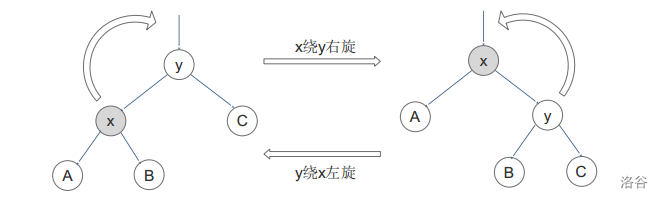
我们要把节点 $x$ 绕着节点 $y$ 左旋或右旋无非就以上这2种情况。
记 $z$ 是 $y$ 的父亲($x$ 的爷爷),其余的编号用法同上面的图。
```rotate``` 分三步:
1. $B$ 和 $y$ 建立父子关系。
2. $z$ 和 $x$ 建立父子关系。
3. $x$ 和 $y$ 建立父子关系。
说白了 ```rotate``` 其实就是 $x$ 代替了 $y$ 的位置,而在此过程中:$x$ 的与 $x$ 作为 $y$ 的儿子左右性相反的儿子($B$)要成为 $y$ 同 $x$ 作为 $y$ 的儿子左右性的儿子,$y$ 要成为 $x$ 与原 $x$ 作为 $y$ 的儿子左右性相反的儿子,$x$ 作为 $z$ 与原 $y$ 作为 $z$ 儿子的左右性相同的儿子($x$ 接替了 $y$ 的位置)。
一开始不大好理解,写的时候画个图。
```cpp
void rotate(long long x){
long long y=f[x],z=f[y],k=chk(x);
c[y][k]=c[x][k^1],f[c[x][k^1]]=y;
c[z][chk(y)]=x,f[x]=z;
c[x][k^1]=y,f[y]=x;
refresh(y),refresh(x);
}
```
------------
4.splay(u,goal):双旋(伸展),u 和 f[u] 一起转直至到 goal 的儿子
Splay 重要操作之二。
双旋是 Splay 的特有操作(你看它都以 DS 自己的名字命名了)。
双旋出现的原因是因为如果只有单旋有可能树高还是很高,如图:
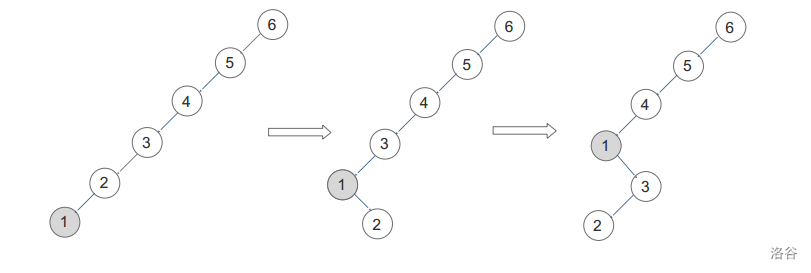
你发现单旋了很多次但是树高没变,相当于 ```rotate``` 成了废物。

所以引入双旋:在 $y$ 成为 $x$ 儿子的同时,$x$ 代替了 $z$ 的位置。
或者你可以理解为 $x$ 和 $y$ 绕着 $z$ 旋转。
双旋有两种情况:
一字形:先 `rotate(y)` 再 `rotate(x)`。
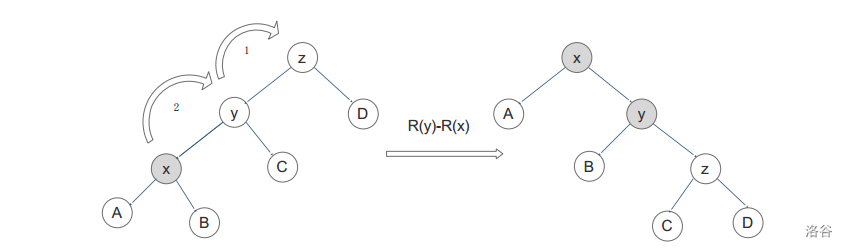
之字形:先 `rotate(x)` 再 `rotate(x)`。
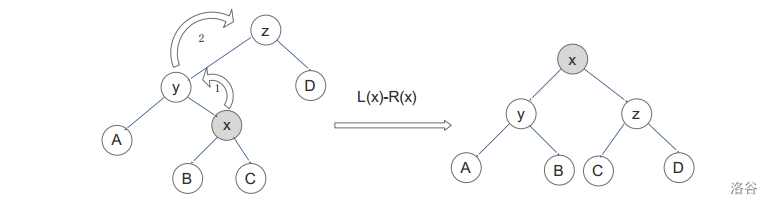
如何判断究竟是一字形还是之字形呢?
简单,一字形就是 $y$ 作为 $z$ 的儿子的左右性与 $x$ 作为 $y$ 的儿子的左右性相同,反之,之字形就是不同。
所以只需要判断 `chk(x)` $\operatorname{xor}$ `chk(y)` 的值就好了。
```cpp
void splay(long long x,long long goal){
if(!goal) rt=x;
long long y,z;
while(f[x]!=goal){
y=f[x],z=f[y];
if(z!=goal) chk(x)^chk(y)?rotate(x):rotate(y);
rotate(x);
}
}
```
还有就是如果我想把节点 $x$ 转到根上,只需要 `splay(x,0)` 即可。
------------
5.add(x):申请一个新建节点的空间,并把其权值赋值为 x
```cpp
long long add(long long x){
w[++tot]=x;
cnt[tot]=s[tot]=1;
f[tot]=c[tot][0]=c[tot][1]=0;
return tot;
}
```
没啥好讲的,至于要返回一个 $tot$ 的原因——我乐意(也就是说你可以不写,但是这样写后面可以省一些码量)。
------------
6.insert(x):在树中插入权值为 x 的节点
思路很简单。从根开始,不断决定向当前节点 $p$ 的左儿子还是右儿子走,同时记录当前节点的父亲 $fp$.如果找到与插入权值大小相同的节点,那直接 $cnt_p++$;否则新申请一个空间,把它作为 $fp$ 的儿子。
为维持平衡,把新建的节点 `splay` 到根。这一点是 Splay 很多操作的特点,或者说是 Splay 本身的特点。
```cpp
void insert(long long x){
long long p=rt,fp=f[p];
while(p && w[p]!=x){
fp=p;
p=c[p][x>w[p]];
}
if(!p){
p=add(x);
if(fp)
c[fp][x>w[fp]]=p;
f[p]=fp;
}
else cnt[p]++;
splay(p,0);
}
```
------------
7.find(x):若权值为 x 的节点存在,则把它转到根。若权值为 x 的节点不存在,则它的前驱或者后继会被转到根。
这个函数看上去非常奇怪,但它是 Splay 许多操作的基础(如:查前驱、查后继、查排名)。
实现的思路和 `insert` 差不多,这里就不再解释了。
```cpp
void find(long long x){
if(!rt) return;
long long p=rt;
while(w[p]!=x && c[p][x>w[p]])
p=c[p][x>w[p]];
splay(p,0);
}
```
------------
8.pre(x):求权值 x 的前驱节点
首先 `find(x)`。
这时候如果根比 $x$ 小,那就说明是 $x$ 的前驱被转到了根上,直接输出。
反之我们需要找根的左子树上最大的值。那么查询节点 $p$ 从 $rt$ 的左儿子开始,能向右走就向右,直至不能走为止,则此时就是答案节点。
```cpp
long long pre(long long x){
find(x);
if(w[rt]<x) return rt;
long long p=c[rt][0];
while(c[p][1]) p=c[p][1];
return p;
}
```
------------
9.suf(x):求权值 x 的后继节点
思路同 `pre(x)`,这里不再多解释。
```cpp
long long suf(long long x){
find(x);
if(w[rt]>x) return rt;
long long p=c[rt][1];
while(c[p][0]) p=c[p][0];
return p;
}
```
------------
10.del(x):删除权值为 x 的数
考虑一件事:如果某个节点是叶节点,那直接把它删了,然后 `refresh` 父节点就可以了。
然后就有了这个操作:
求出 $pr=$ `pre(x)`,$su=$ `suf(x)`。然后 `splay(pr,0),splay(su,pr)`。
上面操作干了什么事?
先把 $pr$ 转到根,再把 $su$ 转到 $pr$ 的儿子(此时一定为右儿子)。
现在我说:$su$ 的左儿子一定为叶节点,而且这个左儿子就是我们要找的 $x$。
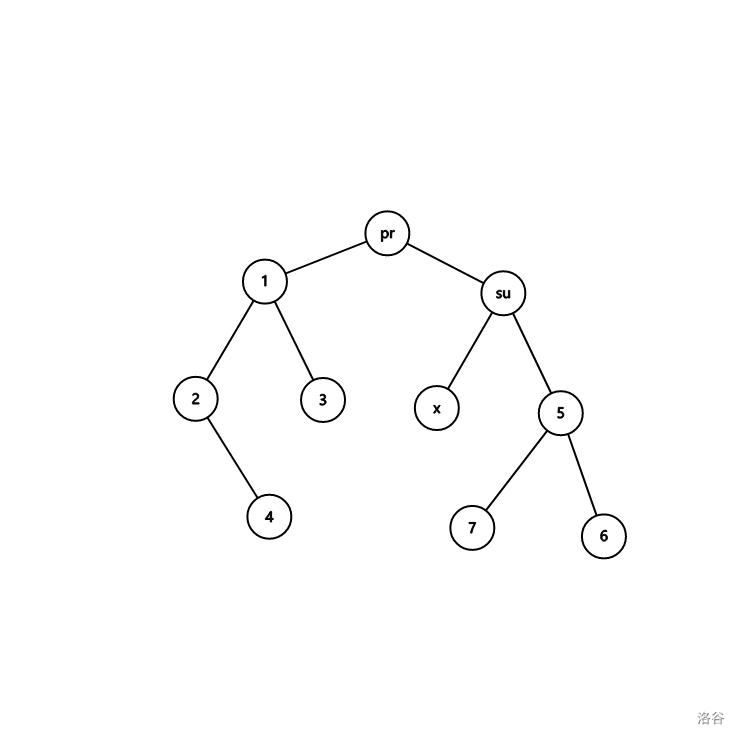
因为树中只有这个点恰介于 $pr$ 和 $su$ 之间,故 $su$ 的左儿子一定为 $x$。
如果 $x$ 有左儿子,则 $su$ 应该在 $x$ 左儿子的位置,不会在根;同理,如果 $x$ 有右儿子,则 $su$ 会在 $x$ 的右儿子。所以 $x$ 一定为叶节点。
搞完这些,我们只需要看看 $cnt_x$ 的大小。如果 $cnt_x>1$,则只需要使 $cnt_x$ 减 1;否则,直接把它删了就好了。
```cpp
void del(long long x){
long long pr=pre(x),su=suf(x);
splay(pr,0);splay(su,pr);
long long p=c[su][0];
if(--cnt[p]){
splay(p,0);
}
else{
c[su][0]=0;
}
refresh(su);refresh(pr);
}
```
但是,考虑一件事情。如果树中只有一个节点,您爆了。
所以为防止这种情况出现,我们在一开始一般会插入无穷小和无穷大的两个节点。初始化如下:(里面还包含了一些其它的初始化)
```cpp
void init(){
long long gx;
tot=0;
gx=add(-2147483647);
gx=add(2147483647);
rt=1;s[1]=2;c[1][1]=2;f[2]=1;
}
```
------------
11.kth(x):查询排名为第 x 的数
简单二分思想。
记查询节点 $p$ 从根开始,如果自己的个数加上左子树的个数比 $x$ 小,那么往右走;否则如果左子树的个数比 $x$ 小,则答案就是 $p$;否则往左跑。
```cpp
long long kth(long long k){
long long p=rt;
while(1){
if(s[c[p][0]]+cnt[p]<k){
k-=(s[c[p][0]]+cnt[p]);
p=c[p][1];
}
else{
if(s[c[p][0]]<k) return p;
else p=c[p][0];
}
}
}
```
------------
12.rnk(x):查询权值 x 的排名。
求排名,那直接求出有多少个数比它小不就是了。把 $x$ 旋到根,输出其左子树大小。由于我们之前插入过一个负无穷,所以我们输出的时候就不加 1 了。
```cpp
long long rnk(long long x){
find(x);
return s[c[rt][0]];
}
```
应注意,这个做法需要保证权值 $x$ 在树中存在。否则,我们应该先把 $x$ 插进去,查询 `rnk(x)`,然后再把它删了。比如在[**P6136 【模板】普通平衡树(数据加强版)**](https://www.luogu.com.cn/problem/P6136)中。
------------
于是我们就学会了 Splay 的所有操作了,你已经完全理解了吧!
```cpp
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
long long m,tot,rt,c[100100][2],f[100010],s[100100],cnt[100010],w[100010];
long long chk(long long x){
return c[f[x]][1]==x;
}
void refresh(long long x){
s[x]=s[c[x][0]]+s[c[x][1]]+cnt[x];
}
void rotate(long long x){
long long y=f[x],z=f[y],k=chk(x);
c[y][k]=c[x][k^1],f[c[x][k^1]]=y;
c[z][chk(y)]=x,f[x]=z;
c[x][k^1]=y,f[y]=x;
refresh(y),refresh(x);
}
void splay(long long x,long long goal){
if(!goal) rt=x;
long long y,z;
while(f[x]!=goal){
y=f[x],z=f[y];
if(z!=goal) chk(x)^chk(y)?rotate(x):rotate(y);
rotate(x);
}
}
void find(long long x){
if(!rt) return;
long long p=rt;
while(w[p]!=x && c[p][x>w[p]])
p=c[p][x>w[p]];
splay(p,0);
}
long long add(long long x){
w[++tot]=x;
cnt[tot]=s[tot]=1;
f[tot]=c[tot][0]=c[tot][1]=0;
return tot;
}
void insert(long long x){
long long p=rt,fp=f[p];
while(p && w[p]!=x){
fp=p;
p=c[p][x>w[p]];
}
if(!p){
p=add(x);
if(fp)
c[fp][x>w[fp]]=p;
f[p]=fp;
}
else cnt[p]++;
splay(p,0);
}
long long pre(long long x){
find(x);
if(w[rt]<x) return rt;
long long p=c[rt][0];
while(c[p][1]) p=c[p][1];
return p;
}
long long suf(long long x){
find(x);
if(w[rt]>x) return rt;
long long p=c[rt][1];
while(c[p][0]) p=c[p][0];
return p;
}
void del(long long x){
long long pr=pre(x),su=suf(x);
splay(pr,0);splay(su,pr);
long long p=c[su][0];
if(--cnt[p]){
splay(p,0);
}
else{
c[su][0]=0;
}
refresh(su);refresh(pr);
}
long long rnk(long long x){
find(x);
return s[c[rt][0]];
}
long long kth(long long k){
long long p=rt;
while(1){
if(s[c[p][0]]+cnt[p]<k){
k-=(s[c[p][0]]+cnt[p]);
p=c[p][1];
}
else{
if(s[c[p][0]]<k) return p;
else p=c[p][0];
}
}
}
void init(){
long long gx;
tot=0;
gx=add(-2147483647);
gx=add(2147483647);
rt=1;s[1]=2;c[1][1]=2;f[2]=1;
}
int main(){
long long i,j,u,v;
cin>>m;
init();
while(m--){
cin>>j>>u;
if(j==1){
insert(u);
}
if(j==2){
del(u);
}
if(j==3){
cout<<rnk(u)<<endl;
}
if(j==4){
cout<<w[kth(u+1)]<<endl;
}
if(j==5){
cout<<w[pre(u)]<<endl;
}
if(j==6){
cout<<w[suf(u)]<<endl;
}
}
return 0;
}
```
<https://www.luogu.com.cn/paste/tc21xjf7>