二项式定理学习笔记

二项式定理好 nan 啊...学了好久，一定是我太菜了 QWQ 这篇博客写的有点杂，主要讲证明，仅供芝士普及 ~~以及颓废娱乐~~ **顺便骗个访客量的说 [→_→](https://www.cnblogs.com/Judge/p/10549495.html)** # 二项式定理的常见形式 emmm...注意这里讲的是常见形式，其实常见形式讲完，一般形式差不多也就学会了吧... ## 课前小插曲 我们定义组合数 $C(n,m)$ 为 $\frac{n(n-1)(n-2)···(n-m+1)}{m!}$ ，这样的定义决定了下面证明的正确性... 然后我们再考虑将原式的 求和函数的 终止条件换一下： $$(x+1)^n=\sum_{i=0}^{\infty} C(n,i) x^i $$ 这时候我们可以知道这个式子和之前是等价的，因为 $i$ 大于 $n$ 的时候 $C(n,i)$ 是等于 $0$ 的 至于为什么要这样表示看到下面你就知道了 ## 一个式子 这个式子大家都见过啦，就是： $$(x+1)^n=\sum_{i=0}^{n} C(n,i) ~ x^i$$ 这个式子为什么是对的呢？（~~显然~~） 我们考虑将左边的式子写成完全形式： $$(x+1)(x+1)···(x+1)$$ 那么我们发现其实可以每次从这 $n$ 个 $(x+1)$ 中选出一个 $x$ 或者一个 $1$ ，然后将 n 个选出来的数字相乘累加进 $ANS$ 那么我们考虑从 $n$ 个 $(x+1)$ 中选出 $i$ 个 $x$ 的情况有多少种呢 这其实就是**组合数**中的 $C(n,i)$，于是乎我们发现原来的式子是正确的 ## 一个应用 我们考虑从 $n$ 个物品中选出选出 $t$ 个物品，那么有多少种选择的方案呢？ （~~既然是二项式定理的应用，那么怎么才能将二项式定理套进去呢？~~） 我们考虑用 $(x^0+x^1)$ 表示某样物品选或者不选（这里 $0$ 次项就是不选，而 $1$ 次项则是选），这两者**相互独立** 那么我们可以根据所有物品**两两独立**，满足乘法定理，于是将它们的选择方案乘起来，也就是 $(x^0+x^1)^n$ 我们考虑一下之前的问题：选出 $t$ 个物品 这里我们把 $n$ 个 $(x^0+x^1)$ 相乘之后 $x^t$ 的系数其实就是方案数了 因为在这里 $x^t$ 只可能来自 $t$ 个**不同的** $(x^0+x^1)$中的 $x^1$， 也就是说它的含义就是我们在 $n$ 个$(x^0+x^1)$中选择 $t$ 个 $x^1$ 然后每次选出一种 $x^t$ 的方案就令 $x^t$ 前的系数加一 ，否则选 $x^0$ 的话就什么也不干 然后我们把 $x^0$ 等价成 $1$，也就是二项式定理的常见形式了 ~~所以说了这么多答案到底是什么！~~ 咳咳，我们发现这里的答案就是 $C_n^t$ 丫！ $C_n^t$ 不就是代表了 n 个里面选 t 个么？ # 指数为负的二项式定理 然后我们考虑一下 $(x+1)$ 的指数推广到 **负数** 的情况 这个时候其实也有： $$(x+1)^{-n}=\sum_{i=0}^{\infty} C(-n,i) ~ x^i=\sum_{i=0}^{\infty} (-1)^i~C(n+i-1,i)~x^i$$ 这时候你可能会非常的惊讶... 组合数里还能带负数的说？！ 其实呢，组合数可以有负的，因为这里的组合数是按之前小插曲里面的定义来的 那么我们考虑怎样转移到最右边的式子： $$C(-n,m)=\frac{(-n)(-n-1)(-n-2)···(-n-m+1)}{m!}$$ 然后我们吧上面的式子里面所有项取反，也就是将他们的**负号**提取出来，就成了： $$C(-n,m)=(-1)^{(-n)-(-n-m+1)+1}\frac{n(n+1)(n+2)···(n+m-1)}{m!}$$ $$ = (-1)^{m}\frac{n(n+1)(n+2)···(n+m-1)}{m!}$$ $$ = (-1)^{m} C(n+m-1,m)$$ （或许你已经看到过上面的式子了） 把原来的式子重写一遍就是： $(x+1)^{-n}=\sum_{i=0}^{\infty}(-1)^i C_{n+i-1}^i~x^i$ # 当加号变为减号 首先的话，我们考虑将上面式子中的 $x$ 取负，那么原式就变成了： $$(1-x)^n=\sum_{i=0}^{\infty} (-1)^i~ C(n,i)~x^i$$ 这个式子...也许大家看到过的吧... 等式后面的表达式其实就是把 $x$ 的负号提了出来，没什么特别的 但是你有没有感觉这个式子有点眼熟？ 没错啊，这和 ***指数为负的二项式定理*** 中长得有点像的，组合数前面都带着个正负号 于是我们试着一下把这里的指数 n 也取负... 那么原式就变成了： $$(1-x)^{-n} =\sum_{i=0}^{\infty} C(n+i-1,i)~x^i$$ 也就是说两个正负号抵消掉了...$QWQ$ **这个式子其实非常有用，它会在你学生成函数的时候派上大用场** （至于生成函数嘛，可以戳[这里](https://www.cnblogs.com/RabbitHu/p/9178645.html)入门，然后戳[这里](https://blog.csdn.net/consciousman/article/details/77935700)深造） # 二项式定理的一般形式 其实上面讲了这么多都是二项式定理的特殊形式（但其实都是比较常见+实用的） 于是下面说说它的一般形式： $$(x+y)^n=\sum_{i=0}^{n} C(n,i) a^i·b^{n-i}$$ 这个东西可以理解为有 n 堆物品，每堆里面有两个物品，价值分别为 x 和 y ，每堆只能选一个物品，要求选择的所有方案价值总和 具体证明就毋须多言了，上面已经证了一大堆了 # 关于广义二项式定理 其实广义二项式定理就是上面的那个式子，我们只要将指数 n 的定义域改成实数就好了 也就是说，广义二项式定理对于实数也成立，也就是： $$(x+y)^α=\sum_{i=0}^{α} C(α,i) a^i·b^{α-i}$$ 而关于 $C(α,i)$ 的值通过小插曲中组合数的定义代就好了 这个真心没什么用！（起码在中学基本用不到这玩意儿）所以也不展开讲辣~ # 论二项式定理在组合数中的运用 这个部分已经跑偏了哟，但内容还是蛮有趣的 ~~(才不是拿来拉篇幅的呢)~~ 我们看到上面的二项式定理中都出现了组合数，那么他们两者之间有什么内在联系呢？或者说我们可以通过二项式定理得出组合数的一些性质么？ 答案当然是肯定的啦！ ### situation 1： 我们考虑吧二项式定理的公式中的 $x$ 、 $y$ 都变成 $1$，那么我们会得到下面这个式子： $$(1+1)^n=\sum_{i=0}^{n} C_{n}^{i}$$ 这能说明什么呢？很明显啊！ 我们考虑前面其实就是 2 的 n 次幂，后面就是 n 个物品里面选出 0~n 个物品的方案数之和，那么由二项式定理可以得知他们两者是相等的 从另一个角度证明， n 个物品里面任意选择物品的方案数等于选 0~n 个物品的方案数之和，即 $\sum_{i=0}^nC_{n}^i$，同时也等于 n 个物品中，每个物品可选可不选的方案，根据乘法定理，方案数为 $2^n$ 那么我们再考虑一下杨辉三角，杨辉三角的第 i 行 第 j 列对应着 $C_i^j$ 上面的相等关系也就说明了杨辉三角的第 i 行所有数之和等于 $2^i$ （这里我们定义杨辉三角中只有一个 1 的行为第 0 行） ### situation 2： 我们再考虑把 x 变成 1， y 变成 -1 ，这两者会产生什么样的反应呢？我们看下面的式子： $$(1-1)^n=\sum_{i=0}^{n} (-1)^i~C_{n}^{i}$$ （注意，不要认为等式左边恒等于 0 ！ 我们默认 $x^0$ 为 1 ，就算是在 x=0 的情况下） 那么我们发现这个等式说明了：除去 $n = 0$ 的情况，**$C_n^i$ 的偶数项之和** 减去 **$C_n^i$ 的奇数项之和** 等于 0 ！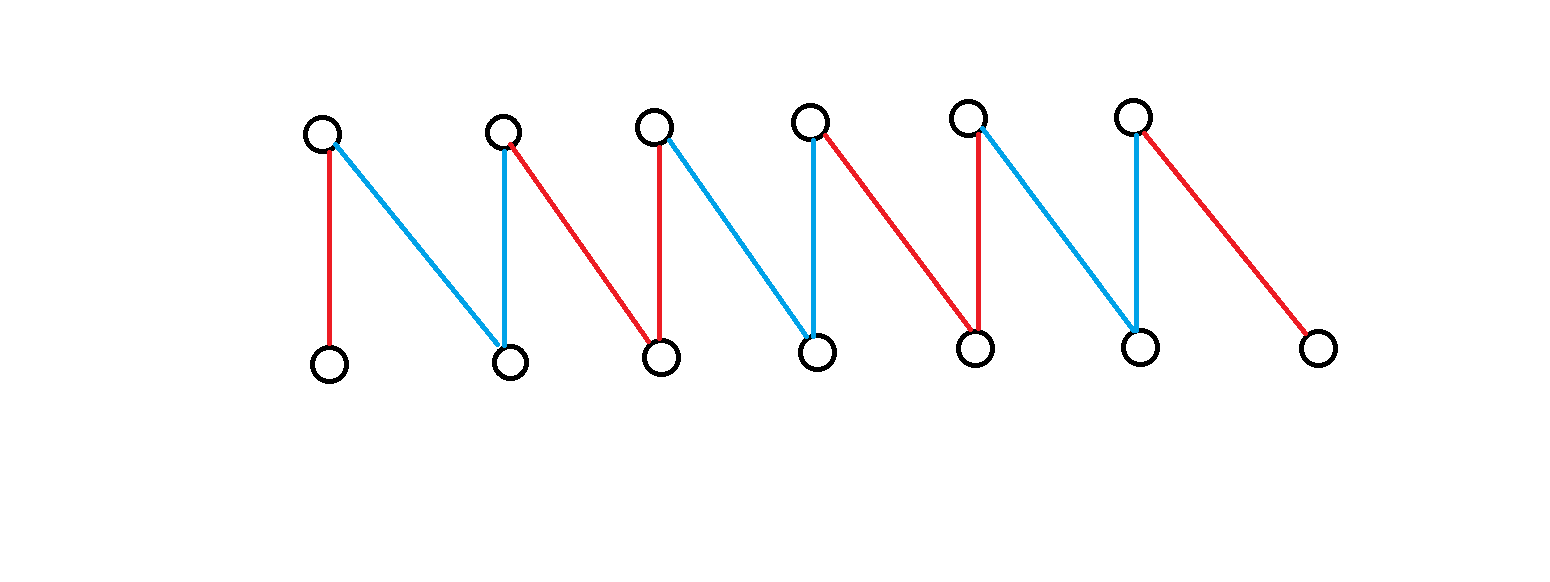 换句话说就是： **$C_n^i$ 的偶数项之和** 等于 **$C_n^i$ 的奇数项之和** 首先考虑 n 为奇数的情况：这时候由组合数的对称性（即 $C_n^i=C_n^{n-i}$）可得原式成立 其次考虑 n 为偶数的情况：每个偶数项对应了上一行所有两个相邻元素之和，那么所有的偶数项就取遍了上一行的所有元素，奇数项同理，所以它们的和都等于上一行的所有元素的和 其实这里上一张图你肯定就懂了  考虑一下杨辉三角，也就是说杨辉三角每一行的 **偶数列对应的项之和** 等于 **奇数列对应的项之和** (由上图也可以看出来) 但是别忘了考虑特殊情况，我们刚刚说过 $n=0$ 除外， $C_0^0=1$ 加上 $n=0$ 的情况，原来的式子就可以这样表达： $$(1-1)^{n}=\sum_{i=0}^{n} (-1)^i~C_{n}^{i}=[n==0]=\epsilon(n)$$ 这里的 $\epsilon$ 就是单位元函数 # 总结 二项式定理很有趣，虽说看着上面的内容貌似没什么用，但等你学到深处就经常会看到它的身影，到那时别忘了再翻开这篇博客，或许你会有新的收获~ 笔芯 $$$$ $$$$ $$$$ $$$$ $$$$ ## 参考资料 貌似都是参考印象中与二项式相关的东西的？