扩展 KMP(Z 函数) 学习笔记
chlchl
·
·
题解
前言
看到模板题里的讲解好像都不大清楚,我也是同时看着 11 篇题解相互理解才大概明白的,就想着写一篇真正通俗易懂的 Z 函数与扩展 KMP 的详解。
本篇博客将以史上最多的图和例子帮大家理解扩展 KMP 与 Z 函数(包括我自己也在进一步理解)。
算法简介
扩展 KMP 是解决 LCP(最长公共前缀)问题的。它可以像 KMP 一样,利用之前得出的信息算出当前需要的信息,可以做到 O(|s|+|t|) 的时间复杂度。
前置知识:KMP 算法(有了基础会好理解一些)。
本篇博客有以下约定:
原理概述及代码实现
以洛谷模板:P5410 【模板】扩展 KMP(Z 函数) 为例。
Part 1:z 函数(t 与 t 匹配的过程)
类似于 KMP 算法的失配数组,扩展 KMP 也具有这样的一个数组:Z 函数(记为 z_i)。它记录的是模式串 t 与 t_{i,n} 的最长公共前缀。
这个图应该对 z 函数解释得很清楚了 QwQ(图丑勿喷)。当然,电脑肯定不是这么求的。
根据这个定义,我们很容易能得到 O(m^2) 的代码:
for(int i=1;i<=m;i++){
while(t[z[i] + 1] == t[z[i] + i]) ++z[i]; //这里是超时的主要原因
}
以上代码虽然是超时的,但是给我们提供了优化思路:我们能不能利用已知的 z 值求出后面的 z 值呢(多图警告)?
假设我们已经知道了 z_1,z_2,\cdots,z_{i-1},要求 z_i。
我们定义 t_{j,j+z_j-1} 为 j(j\in \lbrack 2,i-1\rbrack) 的匹配段(也就是某些博客上的 z-box),并且记使 j+z_j-1 最大的那个 j 为 l,对应的 j+z_j-1 为 r(换言之,r 记录的是当前的信息最远能去到哪里,l 则是去到这个位置的 z 值的下标,即左端点)。
为什么不算 1 呢?因为 z_1=m,那 r=m,就跟暴力一样……
根据上述定义,我们知道 t_{1,z_l}=t_{l,r}(这是 z 函数的定义),如下图红色部分。
现在,我们要求 t_{i,m} 与 t_{1,m} 的最长公共前缀。因为红色段相等,我们可以缩一缩,得到蓝色相等,即 t_{i-l+1,z_l}=t_{i,r}。
此时,我们虽然得出了一个以 i 开头的子串的相关信息,但是却没有整个字符串的前缀,所以我们考虑取 z_{i-l+1} 来传递等量关系。
重要的事情来了:进一步推敲,我们可以得出 t_{1,\ z_{i-l+1}}=t_{i-l+1,\ i+z_{i-l+1}-1}。而又因为上面的蓝色段相等,所以又可以得出 t_{i-l+1,\ i+z_{i-l+1}-1}=t_{i,i+z_{i-l+1}-1},也就是三个绿色的部分相同。
相信这样解释,会比连等好理解一点(我就看着那个连等琢磨了好久)。
注意:上图第一个位置原本是红色,只是绿色的新区域挡住了(后面会给出多个字符串,保证大家把颜色看清楚)。
现在,我们就可以得出 z_i 的值了:
- 若 i+z_{i-l+1}-1\leq r,证明绿色段全部包含在原来的红色段以内,所有的信息都是已知的,所以 z_i=z_{i-l+1}。为什么不用再比较呢?因为如果后面的那个字符是相等的,那么 z_{i-l+1} 必然会更长,所以直接等于就好,如下图所示:
- 若 i+z_{i-l+1}-1> r,\ i\leq r,则我们只能知道 z_i 至少为 r-i+1(因为只有这一段在已知区间内)。随后,暴力从 r+1 和 r-i+1 往后扩展,直到不相同为止。
- 若 i>r,那什么都不用考虑了,全都是未知的,从 1 开始暴力伸展。
问题:这样暴力伸展跟原来复杂度有什么不一样呢?
答案:可以发现,r 是递增的。换言之,一旦 r=m,就不会再出现暴力扩展了,所以最多扩展 m 次,时间复杂度为 O(m)。
有了以上的知识,第一问就可以迎刃而解了。下面,我稍微说一下代码的细节。
先给代码:
void getz(char s[], int len){//1
int l = 0, r = 0;//2
z[1] = len;//3
for(int i=2;i<=len;i++){//4
if(i <= r) z[i] = min(z[i - l + 1], r - i + 1);//5
while(i + z[i] <= len && s[i + z[i]] == s[z[i] + 1]) ++z[i];//6
if(i + z[i] - 1 > r) l = i, r = i + z[i] - 1;//7
}
}
乍一看,这跟之前的讲解怎么如此不一样呢?你的分类呢?这样不是 O(m^2) 的嘛???
一系列的问题,都出自这份代码本身:它本来就是若干次逻辑合并之后的精华,写着很简单,但是却考验各位大佬对 z 函数的理解。
首先,前四行不用解释,分别是函数、定义、初始值和循环。
个人认为,最费解的是第 5 行。
- 对于情况 $1$,由之前的推论得出 $z_i=z_{i-l+1}$。这时,你就会发现第 $6$ 行的 ``s[i + z[i]] == s[z[i] + 1]`` 肯定不成立(之前解释过)。所以无需讨论。
- 对于情况 $2$,由之前的推论得出 $z_i\geq r-i+1$。这时,你就会发现它是有可能进入循环的(因为 $r$ 以后的未知)。
- 为什么取 $\min(z_{i - l + 1}, r - i + 1)$ 就能精准赋值呢?你们回看上面的图,情况 $1$ 时,$i+z_{i-l+1}\leq r$,变化不等式得 $r-i+1>z_{i-l+1}$;情况 $2$ 时,因为 $i+z_{i-l+1}>r$ 啊!所以变化不等式得 $r-i+1\leq z_{i-l+1}$。
第七行就是更新 $l,r$ 了,没啥好说的。
经我这么解释,各位应该理解了吧?
## Part 2:扩展 KMP($s$ 与 $t$ 匹配的过程)
想看这部分,必须对 Part 1 有深刻的理解。
~~因为这部分我不想讲……~~
可以发现,刚刚的 z 函数是两个 $t$ 在匹配。那么我们是不是把其中一个 $t$ 改成 $s$ 就可以了呢?
答案是肯定的。只要把看后缀的那个 $t$ 改成 $s$ 就可以解决。
大概原理如图:
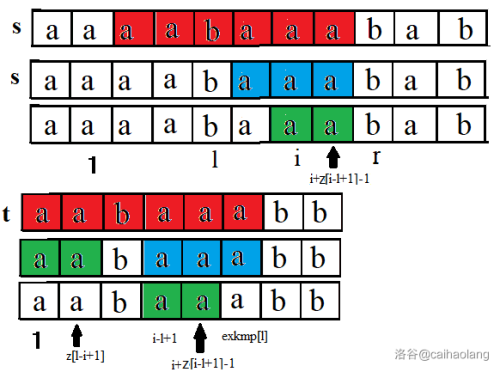
有人会问:为什么取的是 $z_{i-l+1}$ 而不是 $exkmp_{i-l+1}$ 呢?这个问题困扰了我 $10$ 秒:因为我们知道蓝色段相等之后,要找的是 $t$ 的前缀,而并非 $s$ 的前缀。而只有 $z$ 数组是和 $t$ 前缀有关的,所以我们选的是 $z$ 数组而不是 $exkmp$ 数组。
也就是说,该选哪个数组,是根据我们的目标来的。
所以,我们也能很轻松地得出代码(这个数组记为 $exkmp_i$):
```cpp
for(int i=1;i<=n;i++){
if(i <= r) exkmp[i] = min(z[i - l + 1], r - i + 1);
while(i + exkmp[i] <= n && s[i + exkmp[i]] == t[exkmp[i] + 1]) ++exkmp[i];
if(i + exkmp[i] - 1 > r) l = i, r = i + exkmp[i] - 1;
}
```
以上两段代码加个异或和就是 P5410 的正解了(~~然鹅好像有点慢,不过问题不大,不开 O2 也能过~~)。
# 总结
扩展 KMP 确实是一个高效的算法,其核心思想还是根据前面已知的信息推出后面的信息。因此,我们在做题时,可以适当运用这样的思想,进而创造出一些类似的算法。
The End。