浅谈网络流
huayucaiji
·
·
个人记录
浅谈网络流
前言
网络流算法是一个基本上只用记住模板的算法,但是其精髓就在于如何 记忆模板 建立模型,来描述当前的问题。这是网络流的一大难点,也是其最然人着迷的地方,接下来就让我们来康康如何解决网络流问题吧!
什么是网络流?
具体来讲网络流是一个就是一个带权有向图 G=(V,E), 而且对于每一条边 (u,v)\in E 都有一个流量 w(u,v) ,而且在这张图中还有两个特殊的点 s,t,也就是所谓的源点和汇点,而这连个点保证 s,t\in V,s\neq t。网络流算法就是解决计算这两个点之间,满足一系列要求的流量大小。
网络流大体上分为这几个部分:最大流,最小割,二分图匹配,费用流,下面我们来逐一讲述这四个算法。
最大流
代码讲解看这里
最大流所求解得的就是在源点和汇点之间的最大流量。最大流有许多算法,我们只详细讲述Dinic算法,Dinic算法也是我认为最大流算法中最有用的算法了。
Dinic算法
首先我们要了解一些基本概念:
残量网络
对于每一条边我们定义 f(u,v) 为目前流过了 (u,v) 这条边的流量,这条边还剩余的流量为 w'(u,v)=w(u,v)-f(u,v) 由 w'(u,v) 和 V 组成的网络 G' 即为残量网络,即为 G'=(V,{(u,v)\in E,w'(u,v)>0})
<font color=red> 注意:特别的,原图也是一张残量网络(即(u,v)\in G, f(u,v)=0) </font>
增广路
我们先来放一张图:
我们还没有解释什么叫做增广路,增广路 顾名思义 就是在一张残量网络上一条从源点到汇点的路径,比如说在这幅图中:
$S->3->4->T$ 流过流量为 $2$ 的流
$S->3->2->T$ 流过流量为 $1$ 的流
这样总流量就为 $2+2+1=5$ 的流量,也就是本图中的最大流
如果想要更好地体会这个过程,请看这里:[戳我](https://www.bilibili.com/video/av74548650)
了解了这些概念,我们就可以来了解Dinic算法啦!
#### 算法
我们还是看上面这张图,我们首先进行BFS对残量网络进行分层,对于每个点,都有一个 $level$ 值,记录的就是分层后的结果,对于这张图来说,分层结果就是这样的(每个节点的 $level$ 值在节点旁的括号中):

我们来模拟一下这个过程:
1. $S$ 入队,由于是源点, $level[S]=0$;
2. 由 $S$ 可找到 $1,3$,$level[1]=level[3]=level[S]+1=1$;$1,3$ 入队列,$S$ 出队;
3. 由 $1,3$ 可找到 $2,4$,$level[2]=level[4]=level[1]+1=2$;$2,4$ 入队列,$1,3$ 出队;
3. 由 $2,4$ 可找到 $T$,$level[T]=level[4]+1=3$;$T$ 入队列,$2,4$ 出队;
4. 由 $T$ 可找到程序结束的曙光,$T$ 出队;
如果找到了一个节点 $v$,而 $level[v]$ 已经有值了,那么就不再入队列,$level[v]$ 的值也不必再更新。
这就是BFS的全过程啦!是不是很~~简单~~好理解?
接下来我们来看DFS,DFS的作用就是来找到增广路,然后计算结果。如何找增广路呢?我们要利用跟之前的分层结果,只有当 $level[v]=level[u]+1$ 时,我们才会从 $u$ DFS道 $v$。这样保证我们找到的增广路是最短的。
但是,这一定是最优解吗?我们还是看这张图,如果我们用DFS找到的第一条增广路是 $S->3->2->T$ ,流量为 $3$,我们接下来不管怎么找都无法与我们之前提到过的答案 $5$ 大,所以这个算法的正确性是靠运气的,但是我们在考场上我们就需要一个正确性为 $100\%$ 的算法才行所以呢,我们就要研究一个方法,让这个算法变得正确。
我们发现,这个算法最大的问题就是在于如果一旦走错一步,那么我们就几乎无可救药了,所以我们要增添一个“反悔”操作,一旦我们走错了某一步,我们还有机会走回来。那么我们如何实现这个功能呢?我们的方法是建反向边。所有的反向边一开始流量都为 $0$,然后每在残量网络中找到一条增广路,从增广路里的所有边的流量扣去这条增广路上的最大流量 $c_{max}$,所有这条增广路上的边的反向边的流量要加上 $c_{max}$。注意,原图的反向边也可以进入残量网络。还是这张图,我们把原图的边的流量标在"/"前面,反向边的流量标在"/"后面,如下图:

如果我们再次碰到上面的~~坏运气~~情况,我们找到了一条增广路 $S->3->2->T$,按照上面的操作,我们可以得到下面这张图(注意,图中 $level$ 有变化,因为找到这条增广路后图中没有增广路了,所以要重新做BFS):

然后再做DFS时也只能找到一条增广路 $S->1->2->3->4->T$,最大流量为 $2$,然后我们会再得到一张图:

我们发现 $level[T]=-1$ 已经没有增广路了,这样,程序结束,得到答案 $3+2=5$ 是正确的。
为什么呢,其实反向边就是我们所说的“反悔”操作,如果我们找到的增广路里出现了原图的反向边,就相当于把之前从这里流过的流量退回去,知道已经无法“反悔”为止,也就是我们找到了最优解。真是妙哉!
#### 代码
具体代码中的细节我在注释里有讲,可以康康哦。
```cpp
#include<bits/stdc++.h>
using namespace std;
const int maxn=1e4+10;
struct edge {
int v,w,next;
}e[maxn*20];
int n,m,cnt,h[maxn];
void addedge(int u,int v,int w) {
e[cnt].v=v;
e[cnt].w=w;
e[cnt].next=h[u];
h[u]=cnt++;
}//链式前向星不多说了,不会的自己百度
int level[maxn],s,t;
bool bfs() {
memset(level,-1,sizeof(level));
queue<int> q;
q.push(s);
level[s]=0;
while(!q.empty()) {
int u=q.front();
q.pop();
for(int i=h[u];~i;i=e[i].next) {
int v=e[i].v;
if(e[i].w>0&&level[v]==-1) {//保证我们找到的边在残量网络里而且v未被更新过
level[v]=level[u]+1;
q.push(v);
}
}
}
return level[t]!=-1;//如果level[t]=-1,则没有增广路了
}
int dfs(int u,int maxflow) {//maxflow记录的是当前这条增广路上可流过最大的流量。
if(u==t) {
return maxflow;//如果我们到了汇点,则找到了一条增广路。
}
int sum=0;//sum记录当前答案
for(int i=h[u];~i;i=e[i].next) {//~i与i!=-1的效果一样。
int v=e[i].v;
if(e[i].w>0&&level[v]==level[u]+1) {//保证我们找到的边在残量网络里且满足条件。
int flow=dfs(v,min(maxflow,e[i].w));//flow就是我们找到的增广路的最大流量
if(flow>0) {
e[i].w-=flow;
e[i^1].w+=flow;//e[i^1]就是e[i]的反向边,原因可以自己上网查,这里不再赘述
maxflow-=flow;//这条增广路上的的流量要减去flow
sum+=flow;
if(maxflow==0) {
break;//如果最大可行流量为0,那么就结束程序
}
}
}
}
return sum;
}
int main()
{
cin>>n>>m>>s>>t;
fill(h,h+n+1,-1);
for(int i=1;i<=m;i++) {
int a,b,c;
scanf("%d%d%d",&a,&b,&c);
addedge(a,b,c);
addedge(b,a,0);//反向边流量一开始为0
}
long long ans=0;
while(bfs()) {//找到了在目前残量网络的增广路后,重新BFS来分层
ans+=dfs(s,2e9+10);
}
cout<<ans<<endl;
return 0;
}
```
### 应用
我们之前说过网络流的精髓在于如何对问题进行建模,下面的二分图匹配和最小割就是最大流的应用
## 二分图匹配
对于一张图 $G=(V,E)$ 来说,如果我们把点集 $V$ 分成两个无交集的集合 $V_1,V_2$,对于所有的 $(u,v)\in E$, $u,v$ 不能同时属于 $V_1,V_2$ 中的任何一个集合,这样的图,叫二分图,比如说下图:

这里 $V_1=\left\{1,2,3,4\right\},V_2=\left\{5,6,7\right\}$。这样是不是对上面的表达有了更好的理解呢?我们下面再来看一个反面例子:

无论如何分点集 $V$,都无法满足上述的概念,所以这不是二分图。
那么如何判断二分图呢?我们可以运用匈牙利算法,这里不展开说啦,因为对于二分图我们只要知道概念即可。
### [圆桌聚餐问题](http://code.qingtengbc.com/problem/36004)
我们了解了二分图后就可以来看一看题目啦,题目大意我就不概括了。
首先我们很容易想到人与人之间没有关系,桌与桌之间也没有关系,所以能够想到二分图,那么对于样例,我们可以想到这样一个二分图(左边的点代表人,右边代表桌子):
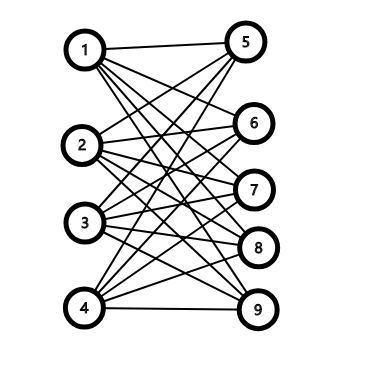
没错,每张桌子和每个人之间都有一条联线,但这有什么用呢?现在我们把源点和汇点加上,桌与人之间的边权为 $1$,人与源点之间边权为这个企业的人数,而桌与汇点的边权为桌课容纳的人数量。

这个图很复杂,然而我们现在要干什么呢。我们要求一遍最大流,然后如果与企业人数和相等,则可以安排,输出 $1$,然后下面的自己贪心搞一搞就好了,否则输出 $0$.
为什么这么做?下面我们来~~玄学地~~理解一下这张图,中间的人与桌的连线边权为 $1$ 是因为题目中要求“为了使代表们充分交流,希望从同一个单位来的代表不在同一个餐桌就餐”,所以流量为 $1$。然而这样求最大流的目的就是为了把所有的人“流到桌子里去”,然而桌子的接受量有限,所以人不能无限制地“流”。如果所有的人“都流掉了”,那么代表是可以把人们安排到桌子去同时也满足要求。
是不是很妙啊?有米有体会到网络流的~~邪恶~~乐趣呢?这个方法叫做“类”最大匹配,这不是真正的最大匹配,那什么是真正的最大匹配呢?它的定义是:对于二分图 $G$,他的一个满足条件的最大子图 $T$ 的边的数量就是最大匹配,满足的要求就是在 $T$ 中,任意两条边没有交点。最大匹配也可以用网络流来解决。这里不再赘述(作者也讲不动了QAQ)
代码:
```cpp
#include<bits/stdc++.h>
using namespace std;
const int maxn=9e4+10,INF=0x7fffffff;
int cnt,h[500],n,m,level[500],s,t;
struct edge
{
int v,w,next;
}e[maxn];
void addedge(int u,int v,int w)
{
e[cnt].v=v;
e[cnt].w=w;
e[cnt].next=h[u];
h[u]=cnt++;
}
void insert(int u,int v,int w)
{
addedge(u,v,w);
addedge(v,u,0);
}
bool bfs()
{
memset(level,-1,sizeof(level));
queue<int> q;
q.push(s);
level[s]=0;
while(!q.empty())
{
int u=q.front();
q.pop();
for(int i=h[u];~i;i=e[i].next)
{
int v=e[i].v;
if(e[i].w>0&&level[v]==-1)
{
level[v]=level[u]+1;
q.push(v);
}
}
}
return !(level[t]==-1);
}
int dfs(int u,int maxflow)
{
if(u==t)
{
return maxflow;
}
int sum=0;
for(int i=h[u];~i;i=e[i].next)
{
int v=e[i].v;
if(e[i].w>0&&level[v]>level[u])
{
int flow=dfs(v,min(maxflow,e[i].w));
if(flow>0)
{
e[i].w-=flow;
e[i^1].w+=flow;
sum+=flow;
maxflow-=flow;
if(maxflow==0) break;
}
}
if(sum==0) level[u]=-1;
}
return sum;
}
int main()
{
int ans=0;
memset(h,-1,sizeof(h));
cin>>n>>m;
s=n+m+1;t=s+1;
for(int i=1;i<=n;i++)
{
int a;
cin>>a;
ans+=a;
insert(s,i,a);
}
for(int i=1;i<=m;i++)
{
int a;
cin>>a;
insert(i+n,t,a);
}
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++)
{
insert(i,j+n,1);
}
}//建图
while(bfs()) ans-=dfs(s,INF);//板子
if(ans==0)
{
cout<<1<<endl;
for(int i=1;i<=n;i++)
{
for(int j=h[i];~j;j=e[j].next)
{
int v=e[j].v;
if(v!=s&&e[j].w==0)
{
printf("%d ",v-n);
}
}
cout<<endl;
}
}//贪心
else cout<<0<<endl;
return 0;
}
```
### [骑士共存问题](http://code.qingtengbc.com/problem/36021)
这道题首先会有人想到八皇后,比如说我。但在他们的做法完全不同。这道题是一道纯的网络流在二分图上的经典应用!首先题目中给了一个非常好的图,是那个棋盘,我们很快就可以看出,在红色格子上的骑士只能攻击黄色格子,这样就可以想到二分图,红色一边,黄的一边(我就不画图了,感觉很恐怖复杂),能互相攻击到的点建流量为 $1$ 的边,再把源点和汇点加上,就建好图了(障碍物不要弄进去)。
那我们要求什么呢?这就是所谓的最大独立集,那什么是最大独立集呢。对于一张图 $G=(V,E)$,选出一个最大的点集 $V'$,满足 $V'\in V$,是的对于任意的 $u,v\in V',(u,v)\notin E$。,具体画图可以百度一下。最大点独立集=点数-最大流。
很显然,这道题就是然我们求最大独立集,这样选出来的点才不会互相攻击。这道题就迎刃而解了。
```cpp
#include<bits/stdc++.h>
#define nc(a,b) (a-1)*n+b
using namespace std;
const int maxn=201*201;
const int dx[]={1,2,-1,-2,1,2,-1,-2};
const int dy[]={2,1,-2,-1,-2,-1,2,1};
struct edge {
int v,w,next;
}e[maxn<<4];
int n,m,cnt,h[maxn];
bool ob[201][201];
void addedge(int u,int v,int w) {
e[cnt].v=v;
e[cnt].w=w;
e[cnt].next=h[u];
h[u]=cnt++;
}
void insert(int a,int b,int w) {
addedge(a,b,w);
addedge(b,a,0);
}
int level[maxn],s,t;
bool bfs() {
memset(level,-1,sizeof(level));
queue<int> q;
q.push(s);
level[s]=0;
while(!q.empty()) {
int u=q.front();
q.pop();
for(int i=h[u];~i;i=e[i].next) {
int v=e[i].v;
if(e[i].w>0&&level[v]==-1) {
level[v]=level[u]+1;
q.push(v);
}
}
}
return level[t]!=-1;
}
int dfs(int u,int maxflow) {
if(u==t||!maxflow) {
return maxflow;
}
int sum=0;
for(int i=h[u];~i;i=e[i].next) {
int v=e[i].v;
if(e[i].w>0&&level[v]==level[u]+1) {
int flow=dfs(v,min(maxflow,e[i].w));
if(flow>0) {
e[i].w-=flow;
e[i^1].w+=flow;
maxflow-=flow;
sum+=flow;
}
}
}
if(!sum) {
level[u]=-1;
}
return sum;
}
int main()
{
//freopen("temp.in","r",stdin);
//freopen(".out","w",stdout);
cin>>n>>m;
memset(h,-1,sizeof(h));
s=0;
t=n*n+1;
for(int i=1;i<=m;i++) {
int a,b;
scanf("%d%d",&a,&b);
ob[a][b]=1;
}
for(int i=1;i<=n;i++) {//建图
for(int j=1;j<=n;j++) {
if(ob[i][j]) {
continue;
}
if((i+j)&1) {
insert(s,nc(i,j),1);
for(int k=0;k<8;k++) {
int x=i+dx[k];
int y=j+dy[k];
if(x<1||y<1||x>n||y>n||ob[x][y]){
continue;
}
insert(nc(i,j),nc(x,y),1e9);
}
}
else {
insert(nc(i,j),t,1);
}
}
}
int ans=0;
while(bfs()) {
ans+=dfs(s,2e9+10);//板子
}
cout<<n*n-m-ans<<endl;//最大点独立集
//fclose(stdin);
//fclose(stdout);
return 0;
}
```
## 最小割
### 算法
最小割就是在一个网络 $G=(V,E)$ 中,找到一张子图 $G'=(V',E')$,其中 $V'\in V,E'\in E$,使得 $\sum_{(u,v)\in E'} w(u,v)$ 最小,这个最小值就是最小割,比如说对于我们上面将最大流的图:

这张图的最小割就是 $w(S,3)+w(S,1)=3+2=5$,当然这张图有多解,这里只给出这一种了。
然而我们发现最小割的值与最大流一样,这不是一个巧合,而是一个定理,所以我们只要能证明它,我们就可以用最大流算法求解最小割了,证明如下:

来自 [OI-WIKI](https://oi-wiki.org/graph/flow/min-cut/)
所以问题就迎刃而解了。用最大流即可解决最小割。
### [方格取数](http://code.qingtengbc.com/problem/36007)
我们现在来将一道例题,这道题首先题意很简单~~虽然我看了20min才看懂qwawq~~,我们可以发现,这道题和上面讲过的骑士共存问题很类似,依然用染色法可以将图构建出来,但构完了图,有什么用呢?
我们把问题转化一下,$c_{取出的最大值}=c_总-c_{不去出的最小值}$,所以我们把问题转化为了求如何取,使得剩下的方格的和最小,这样我们用最小割可以解决问题。
我们让源点指向一个点集,流量为其方格内的点权,而其它点指向汇点,流量也为其点权,相邻的点之间建流量为 $inf$ 的边,是的最小割不会割到这些边上。然后根据之前的定理“最小割=最大流”,我们跑一边 Dinic 即可求出答案。
```cpp
#include<bits/stdc++.h>
#define nc(i,j) (i-1)*m+j
using namespace std;
const int maxn=35,inf=0x7fffffff;
const int dx[]={1,0,-1,0};
const int dy[]={0,1,0,-1};
struct edge {
int v,w,next;
}e[maxn*maxn*maxn*maxn];
int a[maxn][maxn],h[maxn*maxn],level[maxn*maxn],cnt;
int n,s,t,m;
void addedge(int u,int v,int w) {
e[cnt].v=v;
e[cnt].w=w;
e[cnt].next=h[u];
h[u]=cnt++;
}
void insert(int u,int v,int w) {
addedge(u,v,w);
addedge(v,u,0);
}
bool bfs() {
queue<int> q;
q.push(s);
fill(level,level+t+1,-1);
level[s]=0;
while(!q.empty()) {
int u=q.front();
q.pop();
for(int i=h[u];~i;i=e[i].next) {
int v=e[i].v;
if(e[i].w>0&&level[v]==-1) {
level[v]=level[u]+1;
q.push(v);
}
}
}
return level[t]!=-1;
}
int dfs(int u,int maxflow) {
if(u==t) {
return maxflow;
}
int sum=0;
for(int i=h[u];~i;i=e[i].next) {
int v=e[i].v;
if(e[i].w>0&&level[v]==level[u]+1) {
int flow=dfs(v,min(maxflow,e[i].w));
e[i].w-=flow;
e[i^1].w+=flow;
maxflow-=flow;
sum+=flow;
if(maxflow==0) {
return sum;
}
}
}
if(sum==0) {
level[u]=-1;
}
return sum;
}
int dinic() {
int ans=0;
while(bfs()) {
ans+=dfs(s,inf);
}
return ans;
}
int main()
{
//freopen(".in","r",stdin);
//freopen(".out","w",stdout);
cin>>n>>m;
int sm=0;
for(int i=1;i<=n;i++) {
for(int j=1;j<=m;j++) {
cin>>a[i][j];
sm+=a[i][j];
}
}
s=0,t=n*m+2;
fill(h,h+t+1,-1);
for(int i=1;i<=n;i++) {
for(int j=1;j<=m;j++) {
if((i+j)&1) {
insert(s,nc(i,j),a[i][j]);
for(int k=0;k<4;k++) {
int x=i+dx[k];
int y=j+dy[k];
if(x<1||y<1||x>n||y>m) {
continue;
}
insert(nc(i,j),nc(x,y),inf);
}
}
else {
insert(nc(i,j),t,a[i][j]);
}
}
}
cout<<sm-dinic()<<endl;
//fclose(stdin);
//fclose(stdout);
return 0;
}
```
## 费用流
[代码讲解看这里](https://www.bilibili.com/video/BV1tE411L7U2)
### 基本概念
嗯,这是一个新的名词与概念。那么费用流的全称就是“最小费用最大流问题”,也就是在带权有向图 $G=(V,E)$,$\forall(u,v)\in E$,都有一个流量值 $w(u,v)$,和一个费用 $c(u,v)$,这个费用表示的是在这条边上流过单位流量的费用。举个例子:在一条满足 $(u,v)\in E$ 的边 $(u,v)$ 上,当流过大小为 $f(u,v)$ 的流量时(满足 $f(u,v) < w(u,v)$),我们所需要花费的费用是 $c(u,v)*w(u,v)$。那么我们要求的就是在最大化 $\sum_{(u,v)\in E} f(u,v)$时,最小化 $\sum_{(u,v)\in E} c(u,v)$ 我们来看一张图,注意:这一次的图流量与之前的不同哦!!!(~~换图是因为之前那张不太好,最大流只有一种路径 qwawq~~):

对于这张~~水~~图来说,它的最大流很明显是 $6$,但最小费用呢?如果我们选择:
$S->3->2->T$ 费用为 $3\times 2+3 \times 1+3\times 2=15
S->1->2->T$ 费用为 $3\times 1+3 \times 3+3\times 2=18
总费用为 15+18=33。
没有在满足最大流的前提下,比 33 更小的费用了,所以 33 就s是最大流最小费用了。
算法
首先,很显然,这个算法在计算的的同时,我们也能得到最大流,所以我们来介绍一种“类Dinic”算法。
我们发现,对于一条增广路 P,其费用为
C_{total}=\sum_{(u,v)\in P} (\min_{(u,v)\in P} w(u,v))\times c(u,v)
运用乘法分配律:
C_{total}=\min_{(u,v)\in P} w(u,v)\times \sum_{(u,v)\in P} c(u,v)
所以我们以费用为边权跑一遍最短路即可。那怎么建图,我们还是运用之前的 ==“反悔”退流思想== ,如果我们要反悔,我们把费用还回来,所以反向边的费用就是其正向边的费用的相反数。
Q:这样如何保证最大流呢?
A:我们把Dinic算法的BFS部分换成了这里的最短路,因为有负边权,所以可以用SPFA,如果不放心,可以用玄学版Dijsktra把负边权变成正的。因为我们有“反悔”操作,所以就算我们贪心地找到了某一条路径,他的流量太小了,我们就“反悔”,把他的费用给还回来。然后对DFS的内容进行一下改动,这样整个算法就结束了。由于再算最大流时,我们时刻贪心,让费用最小,所以,最后算出来的费用就是最小的了。
接下来,我们就注释里具体来讲每个部分:
#include<bits/stdc++.h>
using namespace std;
const int maxn=5e3+10,inf=0x3fffffff;
struct edge{
int v,cap,cost,next;//cap代表流量,cost代表费用
}e[maxn*20];
int n,h[maxn],cnt,s,t,m,vis[maxn],dis[maxn],mincost;
void addedge(int u,int v,int w1,int w2) {
e[cnt].v=v;
e[cnt].cap=w1;
e[cnt].cost=w2;
e[cnt].next=h[u];
h[u]=cnt++;
}
void insert(int u,int v,int w1,int w2) {
addedge(u,v,w1,w2);
addedge(v,u,0,-w2);//建边
}
bool spfa() {
fill(vis,vis+n+1,0);
fill(dis,dis+n+1,inf);
queue<int> q;
q.push(s);
vis[s]=1,dis[s]=0;
while(!q.empty()) {
int u=q.front();
q.pop();
vis[u]=0;
for(int i=h[u];~i;i=e[i].next) {
int v=e[i].v;
if(e[i].cap&&dis[u]+e[i].cost<dis[v]) {//只有在残量网络里,才做松弛操作
dis[v]=dis[u]+e[i].cost;
if(!vis[v]) {
vis[v]=1;
q.push(v);
}
}
}
}
return dis[t]!=inf;//与Dinic算法里的BFS一样,判断S到T是否还有流量
}
int dfs(int u,int maxflow) {
if(u==t) {
return maxflow;
}
vis[u]=1;
int ans=0;
for(int i=h[u];~i&&ans<maxflow;i=e[i].next) {
int v=e[i].v;
if(e[i].cap&&!vis[v]&&dis[v]==dis[u]+e[i].cost) {//dis[v]=dis[u]+e[i].w就相当于分层。
int flow=dfs(v,min(maxflow,e[i].cap));
if(flow) {
maxflow-=flow;
ans+=flow;
e[i].cap-=flow;
e[i^1].cap+=flow;
mincost+=e[i].cost*flow;//这里与最大流一样,不再赘述。
if(maxflow==0) {
break;
}
}
}
}
vis[u]=0;
return ans;
}
int main()
{
memset(h,-1,sizeof(h));
cin>>n>>m;
s=1;
t=n;
for(int i=1;i<=m;i++) {
int a,b,c,d;
scanf("%d%d%d%d",&a,&b,&c,&d);
insert(a,b,c,d);//建边
}
int ans=0;//记录最大流
while(spfa()) {
ans+=dfs(s,inf);//与Dinic一样的~~~
}
cout<<ans<<" "<<mincost<<endl;
return 0;//结束的曙光
}
总结
那么讲到这里也差不多了,对于网络流的基本算法讲解都讲完了,可能还会有一些大佬会说“怎么没有预流推进啊!”之类的话。我想说的是其实这些优化偏冷门,考场上如果因为这个不会就去骂出题人吧骑士没太大关系,基本也就 20pts 左右,无伤大雅。也很感谢看完的小伙伴们。这篇也花了我5天的时间。谢谢大家啦~~~