题解 AT5142 【[AGC035E] Develop】
Solution
考虑假如
考虑建图,连边
考虑与
-
-
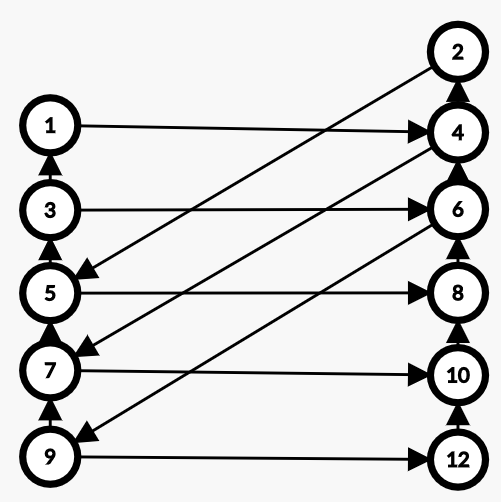
即对于每个奇数
时间复杂度
Code
int n,K,MOD;
int f[MAXN][MAXN],g[MAXN << 1][MAXN][MAXN];
void Solve1(){
K /= 2; f[0][0] = 1;
for(int i = 1;i <= n;i++){
for(int j = 0;j <= K;j++)
addmod(f[i][0],f[i - 1][j]);
for(int j = 0;j < K;j++)
addmod(f[i][j + 1],f[i - 1][j]);
}
int sum1 = 0,sum2 = 0;
for(int i = 0;i <= K;i++)
addmod(sum1,f[n / 2][i]);
for(int i = 0;i <= K;i++)
addmod(sum2,f[(n + 1) / 2][i]);
printf("%lld\n",1ll * sum1 * sum2 % MOD);
}
void Solve2(){
g[0][0][0] = 1;
int cur = 0;
for(int i = 0;i <= n + K - 2;i += 2){
cur = i + 2;
for(int j = 0;j <= n;j++){
for(int k = 0;k <= K + 1;k++)
addmod(g[i + 2][0][0],g[i][j][k]);
}
if(i + 2 <= n){
for(int j = 0;j <= n;j++){
for(int k = 0;k <= K + 1;k++)
addmod(g[i + 2][j + 1][0],g[i][j][k]);
}
}
if(i + 2 >= K + 1){
for(int j = 0;j <= n;j++){
for(int k = 1;k <= K;k++)
addmod(g[i + 2][0][k + 1],g[i][j][k]);
addmod(g[i + 2][0][0],g[i][j][0]);
}
}
if(i + 2 >= K + 1 && i + 2 <= n){
for(int j = 0;j <= n;j++){
for(int k = 0;max(k,j + 1) <= K;k++)
addmod(g[i + 2][j + 1][max(k + 1,j + 2)],g[i][j][k]);
}
}
}
int sum = 0;
for(int j = 0;j <= n;j++){
for(int k = 0;k <= K + 1;k++)
addmod(sum,g[cur][j][k]);
}
printf("%d\n",sum);
}
int main(){
scanf("%d%d%d",&n,&K,&MOD);
if(K & 1) Solve2();
else Solve1();
return 0;
}