堆优化dijkstra
三点水一个各
·
·
个人记录
我也是刚学的QAQ
最近你谷题解不能滥用标题了,那就在这里好好发泄一下。
先来复习一下dijk(明明就是不会)
$pre_{i}$ 是i的前驱(如果需要输路径的话),
蓝点是未确定最短路的点,
白点是已确定最短路的点。
首先标记$dis_{start}$为0,
$dis_{2-n}$ 为INF,
```
for(int i=1;i<=n;i++)
{
找到dis[j]最短的j;
把j变为白点;
枚举与j有边相接的蓝点;
如果当前路比原有路更短,更新;
}
```
用图片理解一下:
( _start_ =1)
开始时我们把$dis_{start}$初始化为0,其余点初始化为INF.
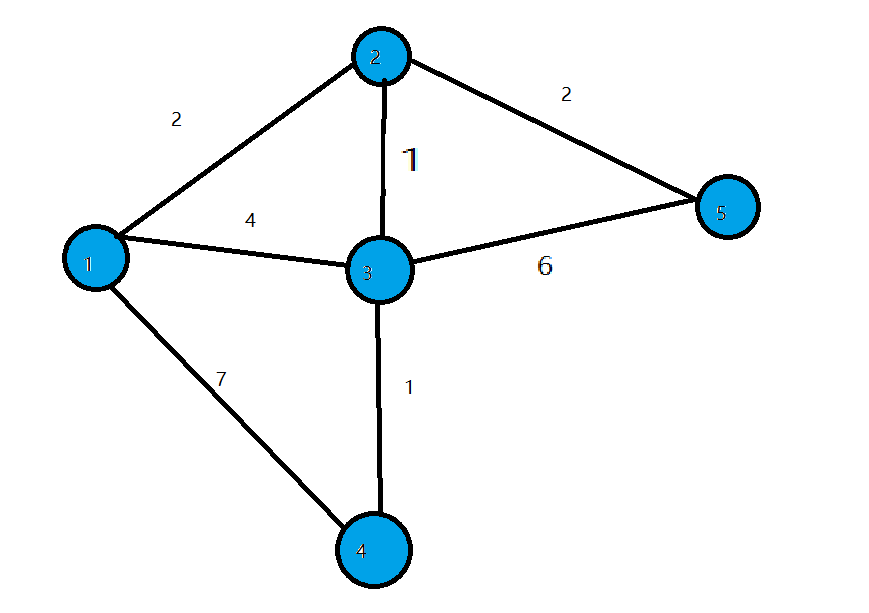
第一轮循环找到 _dis_ 值最小的点1,将1变成白点,对所有与1相连的蓝点的 _dis_ 值进行修改,使得
$dis_{2}$=2 ,$dis_{3}$=4 ,$dis_{4}$=7.
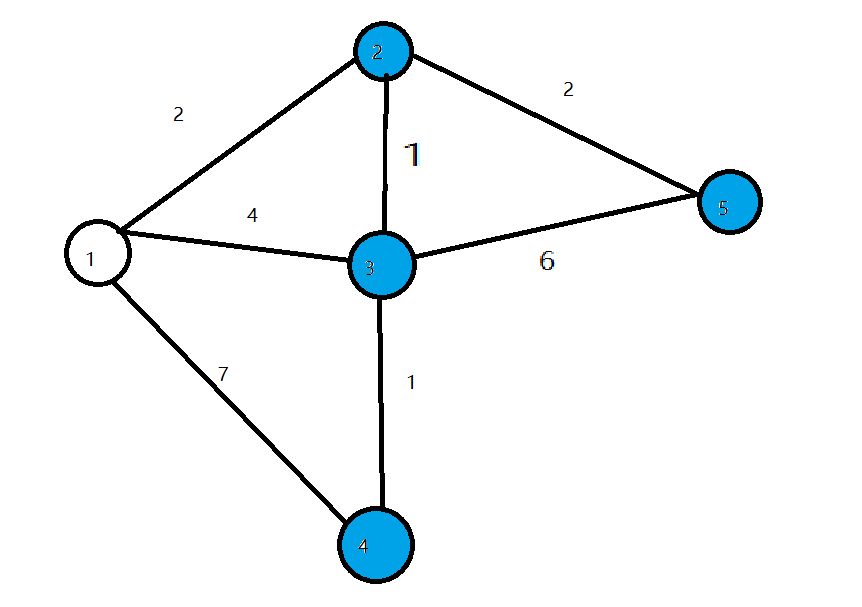
第二轮循环找到 _dis_ 值最小的点2,将2变成白点,对所有与2相连的蓝点的 _dis_ 值进行修改,使得$dis_{3}$=3 ,$dis_{5}$=4 .
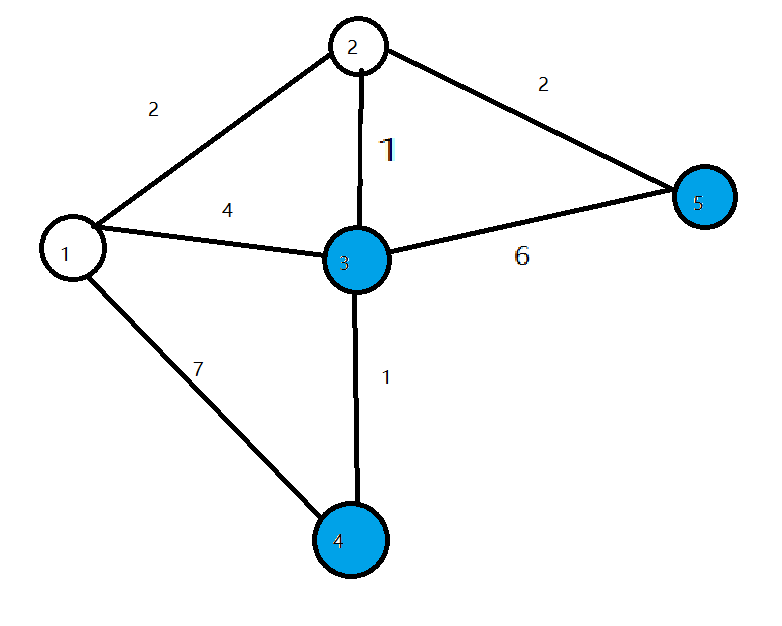
第三轮循环找到 _dis_ 值最小的点3,将3变成白点,对所有与3相连的蓝点的 _dis_ 值进行修改,使得$dis_{4}$=4.
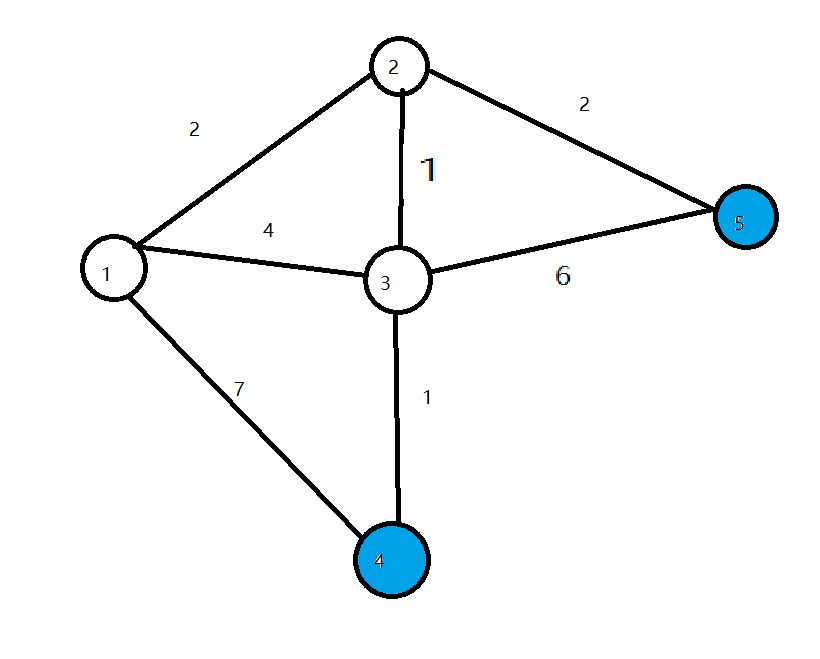
接下来两轮循环分别将4,5设为白点。
完美结束。
时间复杂度O($n^{2}$)。
代码实现:
```
今天我们讲的是堆优化dijk,所以我就不贴代码了。
```
***
## O((n+m) $log_{2}$ n)的堆优化Dijk:
嘿嘿~
STL大法好!
==
每进行`找到dis[j]最短的j;`复杂度为O(n);
但是用priority_queue(优先队列)
取出堆顶元素只需要 O($log_{2}$n) !
为了不重载操作符,
我们用 Pair,
***
### 什么是Pair
标准库函数,就是把两个数据合并成一个数据。
包含在 #include<utility> 中
类模板:template<class T1,class T2> struct pair
参数:T1是第一个值的数据类型,T2是第二个值的数据类型。
功能:pair将一对值(T1和T2)组合成一个值,
这一对值可以具有不同的数据类型(T1和T2),
### 两个值可以分别用pair的两个公有函数first和second访问。
### 操作:
### 创建:
```cpp
pair <string, string> anon;
```
### 初始化:
```cpp
pair <string, string> author("James","Joy");
```
### 赋值:
```cpp
author.first="j";
author.second="k";
```
### 生成新的pair
```cpp
next_auth=make_pair(first,last);
```
***
那么问题来了:
### 如果把pair加进优先队列后会怎么样呢?
是会采用first,还是second呢?
q.top()即是堆顶的值,
### 如果用q.top().first就不管second指按照first排。
***
priority_queue默认大顶堆,而我们要找小的,所以自然就有了
```cpp
make_pair(-dis[y],y)
```
b数组代表白点或蓝点;
to数组存储第i条边指向哪里;
v数组存储第i条边的权值;
next数组表示第i条边的中转点的上一个指向的点;
pre数组一方面作为完成next的目标的附属数组,一方面记录了x点的最后一次指向。
代码:
```cpp
#include<cstdio>
#include<cstdlib>
#include<queue>
#include<utility>
using namespace std;
int pre[100010],to[200010],next[200010],v[200010],dis[100010],n,m,s,x,y,w,l;
bool b[100010];
priority_queue<pair<int,int> >q;
int main()
{
scanf("%d%d%d",&n,&m,&s);
for(int i=1;i<=m;i++)
{
scanf("%d%d%d",&x,&y,&w);
to[i]=y; v[i]=w; next[i]=pre[x]; pre[x]=i;
}
for(int i=1;i<=n;i++)
dis[i]=1e10;
dis[s]=0;
q.push(make_pair(0,s));
while(!q.empty())
{
x=q.top().second;
q.pop();
if(b[x]) continue; b[x]=1;
for(int i=pre[x];i;i=next[i]) //i>0时执行,用以指出x所指向的所有点,也可以用while。
{
y=to[i]; l=v[i];
if(dis[y]>dis[x]+l)
{
dis[y]=dis[x]+l;
q.push(make_pair(-dis[y],y)); //默认大根堆,这里要找小的
}
}
}
for(int i=1;i<=n;i++)
printf("%d ",dis[i]);
return 0;
}
```
嘿嘿,然后你就可以过P3371和P4779了
图片及文字来源:little_sun大佬,https://blog.csdn.net/sevenjoin/article/details/81937695 , 大佬(这个大佬的名字就是空格~ UID56916),