CSP 2023 游记
Exp10re
·
·
生活·游记
前言
来点花絮:
快点端下去罢,去年体育节 cos 过 cxk 力(
CSP 2023 游记。考试当天的纯享版建议往下翻。
我也不知道为什么要写游记,估计是去集训以来的习惯罢。
而长沙集训游记没写完,难绷。
Day -35
初赛,去 SSL 玩。
和 yrj 面基失败,悲。
题目忘了。
打完和同学吹水 92.5 分,然后就和初中同学 @Tony熊孩子 以及 @覃睿 去吃饭了。
Day -21
去长沙集训,传送门。
初赛 69 pts,难评。
Day -13
开学了哎哎哎。
Day -4
学校比较开明,晚修把我们抓去写题。
模拟赛质量还行,关键是,它的主题是东方诶。
在赛时听 \texttt{Feryquitous} 的 \texttt{Arcahv},然后教练说赛时不给听歌!很不爽。
来说一下简要题意和赛时思路,就当题解写了:
T1 flandre
题意:
给出 a_{1,2,\cdots,n} 以及 b_{1,2,\cdots,n},你可以选取其中任意个数并按任意顺序构成排列 A。你需要最大化 f(A)。具体而言,对于有 m 个数的排列 A,有:
\begin{cases}
k &\ (a_{A_i} \lt a_{A_j}) \\
0 &\ (a_{A_i} = a_{A_j}) \\
-k &\ (a_{A_i} \gt a_{A_j})
\end{cases}
给出最大化后的 f(A) 并输出 A。
思路:
贪心秒了。
排序后按照枚举前 i 个数并且按从小到大的顺序放入 A 中,这样可以最大化两个和式。
第二个和式也是可求的,挺好求的,可惜忘了,反正能求。
结果:
过了。110/110 pts。
它卡常,逆天。
T2 meirin
题意:
给出 a_{1,2,\cdots,n} 以及 b_{1,2,\cdots,n},你需要维护 q 次操作:每次操作对 [l,r] 进行一次区间加 k,然后询问以下式子 \bmod\ 1e9+7 的值 :
S=\sum_{l=1}^n \sum_{r=l}^n [(\sum_{i=l}^r a_i)\times (\sum_{i=l}^r b_i)]
思路:
憋憋,我是推式子魔怔人。
记 A 表示 a 的前缀和,B 表示 b 的前缀和,那么对原式进行拆分:
S=\sum_{l=1}^n \sum_{r=l}^n [(A_r -A_{l-1})\times (B_r -B_{l-1})]
S=\sum_{l=1}^n \sum_{r=l}^n (A_r\times B_r+A_{l-1}\times B_{l-1}-A_{l-1}\times B_r-A_r\times B_{l-1})
把好算的扔到一堆,不好算的扔到一堆:
S=\sum_{l=1}^n \sum_{r=l}^n (A_r\times B_r+A_{l-1}\times B_{l-1})-\sum_{l=1}^n \sum_{r=l}^n (A_{l-1}\times B_r+A_r\times B_{l-1})
记:
M=\sum_{l=1}^n \sum_{r=l}^n (A_r\times B_r+A_{l-1}\times B_{l-1})
P=\sum_{l=1}^n \sum_{r=l}^n (A_{l-1}\times B_r+A_r\times B_{l-1})
则:
S=M-P
先尝试拆分 M:
M=\sum_{l=1}^n \sum_{r=l}^n A_r\times B_r+\sum_{l=1}^n \sum_{r=l}^nA_{l-1}\times B_{l-1}
左部仅和 r 有关,右部仅和 l-1 有关:
M=\sum_{i=1}^n i\times (A_i\times B_i)+\sum_{i=0}^{n-1} (n-i)\times(A_{l-1}\times B_{l-1})
M=n\sum_{i=1}^n A_i\times B_i
再尝试拆分 P
P=\sum_{l=1}^n \sum_{r=l}^n (A_{l-1}\times B_r+A_r\times B_{l-1})
记 \displaystyle S_A=\sum_{i=1}^n A_i,\displaystyle S_B=\sum_{i=1}^n B_i。
则
P=S_A\times S_B-\sum_{i=1}^n A_i\times B_i
合并 M+P 有
S=n(\sum_{i=1}^n A_i\times B_i)-(S_A\times S_B-\sum_{i=1}^n A_i\times B_i)
S=(n+1)(\sum_{i=1}^n A_i\times B_i)-S_A\times S_B
对于一次 b 的区间修改对于 B 的修改值总是形如
\{0,0,\cdots,0,k,2k,\cdots,(r-l)k,(r-l+1)k,\cdots,(r-l+1)k\}
的。
这部分对 S_B 的贡献有:
\Delta_B=k\times[(n-r)\times(r-l+1)+\frac {(r-l+1)(r-l+2)} {2}]
记 s 表示 A 的前缀和,S 表示 s 的前缀和。
这部分对 \displaystyle\sum_{i=1}^n A_i\times B_i 的贡献有:
\Delta_M=S_A\times k \times (r-l+1)-(S_{r-1}-S{l-2})\times k
加上即可。
结果:
被卡常了,55/100 pts。
卡大常之后 85/100 pts。
@Jonny09 95 pts,吊打我。/kk
T3 sakuya
题意:
给出一棵带边权的 n 个节点的数,钦定其中 m 个点为特殊点,记为 A_{1,2,\cdots,m}。
你需要维护 q 次询问,每次询问指定一个点 x 并将所有与 x 直接相连的边边权加上 k ,然后随机重排列 A ,求 \displaystyle\sum_{i=2}^{m}\operatorname{dist}(A_i,A_{i-1}) 的期望。
其中,\operatorname{dist}(u,v) 的含义是树上 u,v 两点的最短路径。
思路:
这个期望考虑将其转化为概率。
假定现有由 A 中节点构成的完全图,两点 A_i,A_j 之间的边权为 \operatorname{dist}(A_i,A_j),从其中找到一个遍历所有节点的环,那么每条边被选中的概率为 \frac {m} {\frac {m\times(m-1)} {2}}=\frac {2} {m-1}。
接下来任意删去其中的一条边,得到一条满足题意的路径,每条边被保留的概率就是 \frac {m-1} {m},那么总体而言对于所有情况每条边被选中的概率就是 \frac {2} {m-1}\times \frac {m-1} {m}=\frac {2} {m}。
则总期望值 =
\displaystyle\frac {m!\sum_{i=1}^{m}\sum_{j=i+1}^{m}\operatorname{dist}(A_i,A_j)\times\frac {2} {m}} {m!}
\displaystyle=\frac {2} {m}\times\sum_{i=1}^{m}\sum_{j=i+1}^{m}\operatorname{dist}(A_i,A_j)
\displaystyle=\frac {\sum_{i=1}^{m}\sum_{j=1}^{m}\operatorname{dist}(A_i,A_j)} {m}
DFS 求出 \displaystyle\sum_{i=1}^{m}\sum_{j=1}^{m}\operatorname{dist}(A_i,A_j) 的同时维护每个节点修改 1 时对答案的贡献即可。
具体而言,对于某个节点 x,记其子树个数为 p(包括其祖先及以上的节点构成的子树),每个子树所包含的特殊点个数为 d_i 记其修改 1 对答案的贡献为 f(x),则有:
\begin{cases}
2\times\sum_{i=1}^{p} (p-d_i)d_i &\ (x\notin{A}) \\
2\times(p-1+\sum_{i=1}^{p} (p-d_i-1)d_i) &\ (x\in{A}) \\
\end{cases}
每次操作对答案增加 k\times f(x) 即可。
结果:
赛时没时间打出来了。
回家改了一下,卡卡常就 100/100 pts 了。
T4 忘了
T4 不会,略。
Day -3
上午练习题很水。
中午出去吃饭了。
来写一下下午的模拟赛,很抽象。
T1 魔力屏障
题意:
现有 n 个屏障,第 i 个屏障的强度为 a_i。
你现在可以在任意位置释放强度任意的法术,具体而言,记法术强度为 q:
- 法术会不断往右移动,直到离开所有屏障右方。
- 当法术碰到第 i 个屏障时:若 a_i\leq q,那么摧毁该屏障(此后都会无视 a_i),否则该法术会残留在 a_i 左方。
- 若两个法术相遇,则会合并为一个新法术,强度为被合并的法术强度之和,无论法术在运动中或残留在屏障上。
对于 \forall i\in [1,n],你需要求出打破前 a_i 个屏障所需要的法术总强度最小值。
#### 思路:
赛时口胡 $O(n^3a_i)$ 做法,大致就是区间 $dp$,$f_{l,r,k}$ 表示范围 $[l,r]$ 之内花费 $k$ 能打破所有屏障并且残留一个向右强度为 $f_{l,r,k}$ 的法术。
然后发现不会转移,粗略估算了一下转移大致是 $O(n^5a_i)$ 的,寄,果断跳题。
#### 结果:
没打,0/100 pts。
其他打了错解的都有 55+ pts,犹豫丁真,鉴定为数据太水导致的。
顺便说一下错解:从左往右释放法术,如果不够就补全。
连样例都不能过的写法有 55 pts。/kk
### T2 诡秘之主
#### 前言:
它很迫真地配了一张图:

抽象。
#### 题意:
给定一个长度为 $n$ 的 $0/1$ 序列。
记一个长度为 $m$ 的 $0/1$ 序列权值如下:
- 使用该 $0/1$ 序列生成一个长度为 $m$ 的数列 $b$,其中:若 $0/1$ 序列的第 $i$ 位为 $0$,那么 $b_i=0$,否则,$b_i$ 可以是任意正整数。
- 将 $b$ 按顺序放入一个完全二叉树中,每个数初始位置为根节点,其中:
1. 若当前节点已经有数,若当前数大于该节点上的数,该数移动至右子树,否则移动到左子树。
1. 否则,将该节点权值赋为该数。停止移动。
- 该 $0/1$ 序列的权值为所有可能的 $b$ 数列中,全部放入二叉树后深度最大的节点的深度的最小值。
给出 $q$ 次询问,每次询问给出 $l,r$,询问 $[l,r]$ 的所有子区间的权值和。
#### 思路:
推式子。
发现一个 $0/1$ 序列的权值仅与其第一位 $k$,其中 $0$ 的个数 $cnt_0$,以及其中 $1$ 的个数 $cnt_1$ 有关。其权值 $f(l,r)$ 有:
$$f(l,r)=\displaystyle
\begin{cases}
\min(cnt_0,2+log_2 cnt_1) &\ k=0 \\
\min(cnt_0+1,1+log_2 (cnt_1-1)) &\ otherwise. \\
\end{cases}$$
然后不会了。
在推怎么算 $\displaystyle\sum_{i=l}^{r} C_{i}^{cnt_1}$,发现不好算,直接跳题。
#### 结果
其实这道题写了一半,没写完。
0/100 pts。
没有人拿这道题目的分。/tiao
### T3 Mousetrap
#### 前言:
我习惯叫它 Mousetrap。
因为和 [P4654 [CEOI2017] Mousetrap](https://www.luogu.com.cn/problem/P4654) 是一样的题目。/cf
作为写过两遍的题目当然要场切了。/tiao
#### 题意:
一个人和一只老鼠在进行博弈:
现有一颗 $n$ 个节点的树,钦定两点 $S$ 以及 $T$,老鼠的起点为 $S$。
人和老鼠交替操作,人先手。
人可以进行以下两种操作之一,或者不操作:
- **堵住**一条边。
- 修复一条**被弄脏**的边。人不能修复被自己**堵住**的边。
老鼠则**必须**以以下方式进行操作:
- 如果老鼠所在的节点周围有没被**堵住**或**被弄脏**的边,则**必须**选择一条,移动到该边另一个端点。
- 否则不能行动。
老鼠的目标是最大化人的操作次数,人的目标是最小化操作次数。假定人和老鼠的 $IQ$ 均满足:
$$\displaystyle IQ \geq 114514^{114514^{114514^{114514^{114514^\cdots}}}}$$
你需要求出他们以最优策略行动时,人的操作次数。
#### 思路:
见到两遍了,写一下题解。
这道题目也是我写出的第一道黑题。
以下均为考场思路。
------------
记 $S$ 到 $T$ 的路径为主干道,与主干道直接相连且不在主干道上的边为支路。
手玩一下发现人和老鼠的操作必定按照下面四个步骤依次进行:
1. 老鼠沿主干道移动,同时人堵住一条支路。
2. 老鼠在某个节点沿一条支路进入一个子树,然后被自己弄脏的边堵死在某个叶子结点。
3. 人在老鼠被堵死的时候堵住老鼠当前位置到 $T$ 的路径上的所有支路,然后清理老鼠当前位置到 $T$ 的路径上所有被弄脏的边。
4. 老鼠此时只能走到 $T$,游戏结束。
步骤 1 和 3 的人的操作比较难模拟,注意到操作 2 是树上操作,可以用树形 DP 来计算,那么先考虑操作 2。
记 $f_x$ 表示若老鼠进入该树根节点后,在该树内的操作数。
考虑当某个节点的所有子树都计算完毕后,老鼠进入该节点时人类的操作:
- 如果人类不堵与 $f$ 最大的子树相连的边,那么老鼠肯定会走这条边,到达 $f$ 值最大的子树。
- 否则,老鼠会进入 $f$ 值次大的子树。
显然让老鼠进入 $f$ 值次大的子树一定比老鼠进入 $f$ 值最大的子树好,那么转移就应该从 $f$ 值次大的子树进行转移。
老鼠进入该子树后,在操作 3 时还需要堵住其其他支路。可以直接在此处计算。那么转移方程显然:记 $cnt_x$ 表示 $x$ 子树个数,$son_x$ 表示 $x$ 的某个子树,则有:
$$f_x=\underset{y\in son_x}{\operatorname{2ndmax}}{f_y}+cnt_x$$
把步骤 2 考虑完之后尝试考虑步骤 3,假定老鼠在步骤 2 中从节点 $p$ 进入子树 $x$ 然后被困死,那么从 $p$ 到 $T$ 的所有支路都必须堵住。这个可以用前缀和维护,不多赘述。
步骤 1 堵路的操作比较难想,这时我们可以转换思路。注意到答案具有单调性,可以二分答案转化成判定性问题。
假定老鼠走主干道已经到达了某个节点 $p$,它得知你期望的操作次数为不大于 $m$,那么考虑老鼠会如何进入子树。
如果现在已经堵住了 $u$ 次路,对于某一个子树 $x$,老鼠只会在 $f_x+sum_p+u \gt m$ 的情况下才会钻进这个子树。
正确性证明:若 $f_x+sum_p+u \leq m$,那么老鼠进入这个子树后,人必定能用 $f_x+sum_p+u$ 次操作完成游戏,由此说明人可以在 $m$ 次操作内完成游戏。在目标明确的情况下,老鼠的目的就是证明人不可以在 $m$ 次操作内完成游戏。因此,进入该子树一定对老鼠不优。
既然对于每个子树钻或不钻对于老鼠而言是一定的,那么人的操作就显然了:人需要按照从 $S$ 到 $T$ 的顺序堵住所有老鼠可能会进入的子树与主干道的相连边。如果老鼠在到达某个节点的时候还有可钻的子树,那么说明答案大于 $m$,否则 $m$ 就是一个可行的答案。
至此,这道题的思路就明确了。
代码扔到[剪贴板](https://www.luogu.com.cn/paste/dxxn46jf)了。
题解同步于博客 [P4654 [CEOI2017] Mousetrap 题解](https://www.luogu.com.cn/blog/Exp10re/solution-p4654)。
#### 结果:
评测机吃答辩了,满分代码跑出 72/100 pts。
std 也是 72/100 pts,乐。
### T4 忘了
Exp10re 的记性远小于金鱼。
不会,略。
## Day -2
就剩两天了喂。
早上题目改不了一点,去写了会 CF 1800 分段的题目。
写了一篇题解,补全了上边 [P4654 [CEOI2017] Mousetrap](https://www.luogu.com.cn/problem/P4654) 的题解,晚上发了。
为什么 CSP 模拟赛会有这么一道题啊(
先补全 Day -2 下午的模拟赛:
没有推式子题,所以题解很短。
名字忘了。
### T1 情景剧
#### 题意:
给定一个长为 $n$ 的数列 $a$,最大化 $\max(a_{l,l+1,\cdots,r})\times\min(a_{l,l+1,\cdots,r})\times(r-l+1)$。
$1\leq n\leq 2\times10^6,1\leq a_i \leq 10^9$。
#### 思路:
赛场上没想到好的做法,直接两个 ST 表加分治水分。
可是会爆空间呃呃,调小空间水了 50 pts。
按理来说改单 st 表能有 100 pts,但是没想。
#### 结果:
没挂分,50/100 pts。
@[SilverWolf_Real](https://www.luogu.com.cn/user/286571) 写了 [情景剧题解](https://www.luogu.com.cn/blog/nngunuai/qing-ying-ju-ti-xie),吊打我。/bx/bx/bx
### T2 抽卡
#### 题意:
现有一个长度为 $n$ 的数列 $A$ 以及 $m$ 个限制,你需要在限制条件下生成一个数列 $B$。每个限制形如 $(d,A_p)$,表示限定 $B$ 的第 $d$ 位必须为 $A_p$。
现在给出 $q$ 次询问,每次询问先给出以下两种操作之一:
- `1 t` 表示删除 $B$ 的第 $d$ 位的限制。
- `2 t x` 表示限定 $B$ 的第 $t$ 位必须为 $x$。
然后你需要重新排列 $A$ 组成 $B$,使得 $B$ 满足给出的限制,并且最小化:
$$S=\sum_{i=2}^{n} [B_i \bmod 2 \ne B_{i-1} \bmod 2]$$
的值。输出这个最小化后的值。
#### 思路:
是很显然的权值线段树题目。
注意到答案仅与选用的数的奇偶性相关,那么考虑对 $A$ 中的数进行奇偶计数。
用线段树维护每个位置向左及向右的第一个限制位置,于是一次添加删除操作的时间复杂度都是 $O(n \log n)$,而且每次操作都能 $O(1)$ 计算与两边的距离。
维护部分的代码扔到[这里](https://www.luogu.com.cn/paste/l9ldxv0f)。
注意到固定一部分边之后答案只与两边奇偶性相同的空段,两端的空段以及剩余的数中奇数(偶数)数量相关。
- 在两边奇偶性相同的空段中加入任一奇偶性不同的数会使答案 +2。
- 在两端的空段中加入任一奇偶性不同的数会使答案 +1。
尝试将剩余的数填入空段中,特判两端的空段,对于奇数和偶数,考虑最多能填满多少个奇偶性相同的空段。那么问题就变为求得最大的 $p$ 满足:
$$\sum_{i=1}^{p} a_{1/0,i} \leq K_{1/0} (p \leq m_{1/0})$$
其中,$a_{1/0}$ 表示该奇偶性下的空段长度集合升序排序后的序列,$m_{1/0}$ 表示该序列长度,$K_{1/0}$ 表示还未固定的,该奇偶性的数的个数。
这个玩意显然可以用权值线段树维护!权值线段树简直就是神!
嘿嘿嘿我的线段树嘿嘿嘿。
就这样了。
#### 结果:
赛时没打出权值线段树,但是有 30/100 pts,很诡异。
### T3 0/1 序列修改
#### 题意:
给定一个 $0/1$ 序列,你需要反转其中的若干位使得其每两个相邻的 $1$ 满足其距离(距离定义为 $|r-l+1|$,其中 $r$ 和 $l$ 是两个相邻的 $1$ 的下标)均为 $d$ 的倍数。求最小操作次数。
#### 思路:
很简单的余数计数。
对下标 $\bmod\ d$ 的余数进行计数,保留余数计数最大的一个,删除其他 $1$ 即可。
签到题啊啊啊。
#### 结果:
100/100 pts。
好像是这几天唯一一道签到题?
### T4 虚树
忘了,略。
## Day -1
早上一直在写博客,写完了游记去写了 [同余最短路笔记](https://www.luogu.com.cn/blog/Exp10re/mod-shortest-path)。
非常好博客,使我的脑子旋转。/tiao
不写了,休息一天半。
## Day 0
$$\texttt{So that's the day.}$$
没吃早餐。
早上复习了一下 tarjan,然后出门吃了饭。
中午尝试睡觉,结果没睡着。/tiao
紧张?倒没有。
其实睡不着的原因更多可能因为睡前下了一把国际象棋,天胡局不知道为什么被对面升变了一个后(
下午一点坐校车去 SSL。
车上睡不着,和 @[nczxjiangyihao](https://www.luogu.com.cn/user/600774) 打了若干把 KARDS。K 牌好玩。
入场前教练给我们一整个学校拍了照,然后我们都在猜照片里最高分 $\times$ 最低分 $\times$ 人数等于多少。
鉴定为写情景剧写的。/kk
没什么可说的了,就复盘一下赛时思路吧:
### #0 开赛 14:30
开赛前半小时一直在看题。
给隔壁的哥们吓傻了。
顺便说一下:对 PDF 密码很不满,那个 $z$ 写的跟个 $2$ 一样。
他的密码比我的用户名都阴间。/tiao
### #1 开赛半小时 15:00
当时的情况大致是这样:
整理了一下思路,发现 T3 完全不会。
猜做法:
T1 暴力 100 pts。
T2 括号匹配 不知道多少 pts。
T3 不会。大模拟能不能爬出 CSP。/kk
T4 一眼二分 + 树形 DP,但是具体怎么做还不是很明朗。
所以先开 T1:
------------
### T1 密码锁
#### 题意:
现有一个五位数密码。
可以进行一次操作,操作为:指定一个数 $x\in[1,9]$,然后将其某一位或连续两位的数均加上 $x$,然后对 $10$ 取模。
给定 $n$ 个操作后产生的数,你需要求出原密码的可能情况数。
#### 思路:
注意到操作可逆。
对于每个新的密码再根据操作规则再逐个旋转一遍,对产生的新数进行计数。
显然有 $n$ 个计数的都是可能的原密码,统计一遍即可。
时间复杂度 $O(81n+1\times 10^5)$。理论而言能省去 $O(1\times 10^5)$,但是既然稳过了那么就不优化了,浪费时间。
------------
给 T1 加了点注释。我喜欢注释。
### #2 开赛 45 分钟 15:15
T4 瞪眼没瞪出来,所以先开 T2。
然而体感觉得 T4 比 T2 简单,令人感叹。
------------
### T2 消消乐
#### 题意:
现有一个长度为 $n$ 且仅由小写字母组成的字符串 $S$。
记每次操作可以从字符串中删除两个相邻的相同字符,操作后剩余字符串会拼接在一起。
我们称一个字符串是可消除的,当且仅当可以对这个字符串进行若干次操作,使之成为一个空字符串。
求这个字符串的所有非空连续子串中,有多少个是可消除的。
#### 思路:
首先是 $O(n^3)$ 做法:暴力枚举子串的左右端点,然后 $O(n)$ 进行括号匹配,计数,结束。
$O(n^3)$ 做法难以优化。
考虑 $O(n^2)$ 做法:注意到可消除的串有若干个性质:
- 对于某一位 $i$ 的字母 $S_i$,若能找到后面某一位 $j$ 满足 $S_j=S_i$ 且 $S_{i+1,\cdots,j-1}$ 为可消除的串,那么显然 $S_{i,i+1,\cdots,j-1,j}$ 也为可消除的串。
- 若 $S_{i,i+1,\cdots,j-1,j}$ 以及 $S_{j+1,\cdots,k-1,k}$ 均为可消除的串,那么 $S_{i,i+1,\cdots,k-1,k}$ 也为可消除的串。
记 $r_i$ 表示以 $i$ 开头往后的最短的可消除的串的结尾位置之后的一个位置。即:记 $K$ 是满足 $S_{i,i+1,\cdots,k-1,k}$ 为可消除的串的最小的 $k$,那么 $r_i=K+1$。特殊的,如果没有 $k$ 满足 $S_{i,i+1,\cdots,k-1,k}$ 为可消除的串,则 $r_i=i$。
记“跳一次”表示在 $i$ 进行一次操作,使得 $i\leftarrow r_i$,“跳一次失败”表示尝试在 $i$ 进行一次操作,但 $r_i=i$,此时显然跳一次不会改变 $i$。
根据上述性质,有:若当前尝试枚举由 $l$ 开始的所有可消除串,那么可以由以下方式计算得出:
- 从 $l+1$ 开始跳若干次,直到当前达到的位置 $k$ 满足 $S_l=S_k$,此时显然 $r_l=k+1$。
- 如果找不到满足条件的 $k$ 或者跳若干次后跳一次失败了,那么 $r_l=l$,即由 $l$ 开始的可消除串个数为 $0$。
- 否则,计算出从 $l$ 开始成功跳一次的次数,这个次数就是由 $l$ 开始的可消除串个数。
时间复杂度大致为 $O(n^2)$,确切而言为 $O(ans)$。
那么 $O(n)$ 做法不难得出:对于每个位置 $i$ 维护跳的过程中的位置的字母计数,记从 $i$ 开始跳的过程中字母 $c$ 出现了 $cnt_{i,c}$ 次,则有优化:
- 对于当前位置 $l$,若 $cnt_{l+1,S_l}=0$,那么显然从 $l+1$ 开始跳一定无法找到 $k$ 满足 $S_l=S_k$。直接设 $r_l=l$ 即可,此时 $l$ 显然不产生计数,$cnt_{l}$ 仅 $S_l$ 有一次计数。
- 否则,由 $l$ 开始的可消除串个数 $=\displaystyle1+\sum_{i='a'}^{'z'} cnt_{r_l.i}$。转移将 $cnt_{r_l}$ 直接复制到 $cnt_{l}$,然后使 $cnt_{l,S_l}$ 计数 $+1$ 即可。
时间复杂度 $O(26n)$,能过。
------------
切这道题的时候上了两次厕所。
先想了一个小时的 $O(n^2)$ 不会,然后发现能优化。
最后打了两个小时。
### #3 开赛 2 小时 16:30
剩下的时间开 T3 一定悬。
T3 还是没看懂题目。
然后有这么一瞬间发现 T4 答案满足单调性!
直接开一手 T4。
------------
### T4 种树
#### 题意:
题意开摆了,不简化了。
------------
你是一个森林养护员,有一天,你接到了一个任务:在一片森林内的地块上种树,并养护至树木长到指定的高度。
森林的地图有 $n$ 片地块,其中 $1$ 号地块连接森林的入口。共有 $n-1$ 条道路连接这些地块,使得每片地块都能通过道路互相到达。最开始,每片地块上都没有树木。
你的目标是:在每片地块上均种植一棵树木,并使得 $i$ 号地块上的树的高度生长到不低于 $a_i$ 米。
你每天可以选择一个未种树且**与某个已种树的地块直接邻接**(**即通过单条道路相连**)的地块,种一棵高度为 $0$ 米的树。如果所有地块均已种过树,则你当天不进行任何操作。特别地,第 $1$ 天你只能在 $1$ 号空地种树。
对每个地块而言,从该地块被种下树的当天开始,该地块上的树每天都会生长一定的高度。由于气候和土壤条件不同,在第 $x$ 天,$i$ 号地块上的树会长高 $\max(b_i + x \times c_i, 1)$ 米。注意这里的 $x$ 是从整个任务的第一天,而非种下这棵树的第一天开始计算。
你想知道:最少需要多少天能够完成你的任务?
------------
#### 思路:
考虑将森林视为以 $1$ 为根的树。
显然,对于每一个地块,在确定其生长至 $a_i$ 的时间之后一定可以唯一确定其最晚被种下的时间。暂时记为 $d_i$。
于是问题就分为了三步:
- 二分可能的结束时间,对结束时间进行正确性证明。
- 计算对于当前的结束时间每个地块的 $d_i$ 值。
- 判定对于计算出的 $d_i$ 是否有满足条件的种植方案。
第一步进行基础二分即可。
第二步不是很会,在场上我是又套用了一个二分进行计算的。破一元二次不等式谁想算谁算(
第三步的话可以考虑贪心 + 树形 DP。
具体的,对于树上某个地块,对于其每某个个儿子,最晚被种下的时间为 $d_y$ ,那么其本身最晚被种下的时间就最小为 $d_y-1$。
则有:对于某个地块 $x$,转移方程为:
$$d_x=\max{(d_x,\underset{y\in son_x}{\max}{d_y}-1)}$$
那么从 $1$ 开始,将其每个儿子的 $d$ 值扔进单调栈中,然后每次往单调栈栈顶所表示的节点位置走即可。
时间复杂度 $O(n\log^2 n)$。
------------
然而最后还是没推出来第二步的计算方法,令人感叹。
二分应该没假。
输出的时候发现输出 $\frac {Ans} {2}+1$ 正好能过三个大样例,但过不了小样例,无所谓直接交了。/kk
最后没时间了,交卷。
------------
于是 CSP 2023 结束了。
无论结果如何,希望大家都能在 OI 这条路上一直走下去。
------------
## 后记
和初中同学 @[Tony熊孩子](https://www.luogu.com.cn/user/545902) 以及 @[覃睿](https://www.luogu.com.cn/user/311649) 去吃饭了。前后呼应属于是。
比完赛和同学口嗨估分,我估的是 $Score\in[200,300]$。部分分大致就是 $100+100+0+40=240$ 左右。
最后在其他平台测试,有两个的估分都是 $200$,你谷估分 $215$。谷好闪,拜谢谷。
------------
在 T3 代码写了如下内容:
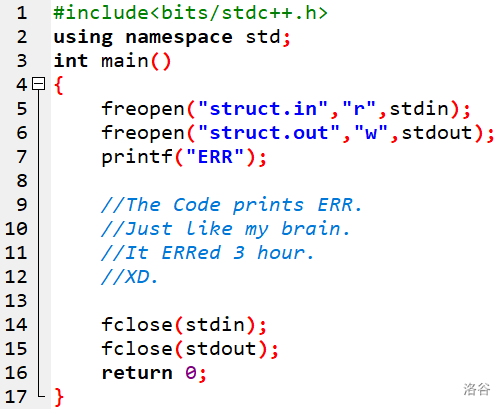
令人感叹的、
------------
代码被选入 [GD CSP 2023 迷惑行为大赏](https://www.luogu.com.cn/blog/Lotuses/csp-2023-mi-huo-xing-wei-tai-shang) 了。大致就是这么几行:
```cpp
//I'm Exp10re, Luogu UID is 403069, subscribe me :).
//Wait, how do you know segtree is cute.
```
为什么都关注我打的广告,线段树难道不可爱吗。/fn
所以,加入 [线段树同好会](https://www.luogu.com.cn/team/64778) 和我一起发电罢!
------------
然后就要写 [NOIP 2023 游记](https://www.luogu.com.cn/blog/Exp10re/noip-2023) 了,不知道算不算半场开香槟。
那么祝各位好运。再见。
------------
$$\color{#ff0001}\texttt{咕}\color{#996600}\texttt{者}\color{#669900}\texttt{,鸽}\color{#55aa00}\texttt{也。}$$
$$\textcolor{green}{\small\text{\color{#ff0001}{\texttt{哦}}}\huge\text{\color{#ff0000}{其}}_{\small\text{\color{#aa5500}{\texttt{已}}}^{\large\text{\color{#996600}{经}\color{#996600}{快}}\small\texttt{\color{#887700}{被}\color{#778800}{写}\color{#669900}{完}}}}^{\large\text{\color{#ee1100}{}}{\small\texttt{\color{#dd2200}{ 实}\color{#cc3300}{这}}\large\texttt{\color{#cc3300}{游}\color{#bb4400}{记}}}}\huge\text{\color{#55aa00}{了}}}$$
$$\color{#ff0001}\texttt{咕}\color{#996600}\texttt{咕}\color{#669900}\texttt{咕}\color{#55aa00}\texttt{咕!}$$