QOJ 5507. Investors
2huk
·
·
题解
快进到重点:
给定 a_1 \dots a_n。将去划分成 k + 1 段,使得每段的逆序对数量之和最小。0 \le k \le n \le 6000。
直接 DP。设 w_{i, j} 表示 a_i \dots a_j 的逆序对数量,f(i, j) 表示 1 \sim j 被划分了 i 段的答案。那么:
f(i, j) = \min \{f(i-1,k-1) + w_{k, i}\}
- 为什么满足四边形不等式?
我们考虑四个点 $a < b < c < d$。如果 $(i, j)$ 是一个逆序对,我们分类讨论它们的位置,以及对交叉和包含两种情况的贡献:
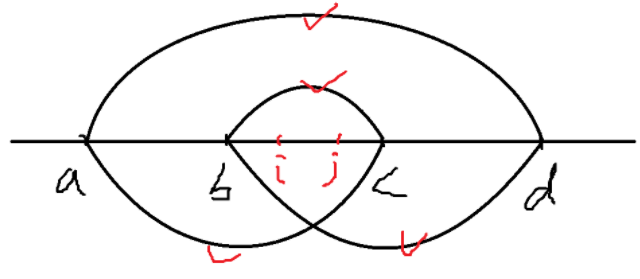
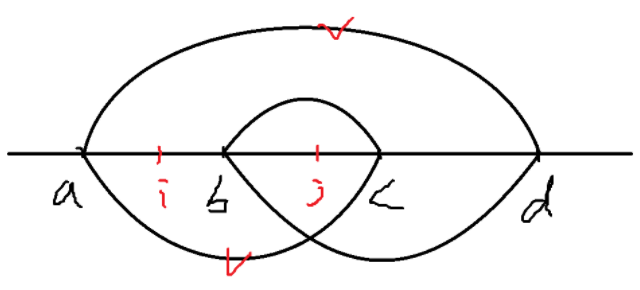
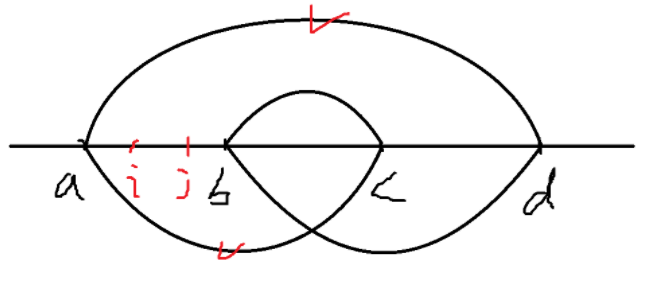
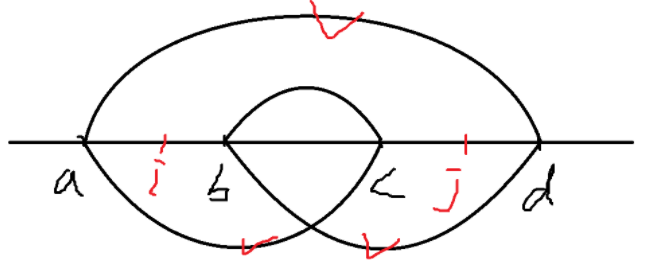
打勾表示对这个区间有贡献。当然还有一些对称的情况没列举。
不难发现交叉优于包含。
- 怎么分治转移?
首先按层求解,即先求解 $i - 1$ 的所有状态再算 $i$ 的所有状态。
定义函数 $\text{solve}(l, r, ql, qr)$ 表示,我们希望用 $ql \sim qr$ 这些决策点,求解出 $f_{i,l}\dots f_{i,r}$ 的值。
首先暴力求出 $mid = \lfloor \frac {l+r}2 \rfloor$ 的状态值,以及决策点 $M$。然后执行 $\text{solve}(l,mid-1,ql,M)$ 和 $\text{solve}(mid+1,r,M,qr)$ 即可。
```cpp
#include <bits/stdc++.h>
using namespace std;
const int N = 6010;
typedef long long ll;
int n, k, a[N];
ll w[N][N]; // [l, r] 内的逆序对数
ll f[N][N];
void solve(int k, int l, int r, int ql, int qr) {
if (l > r) return;
int mid = l + r >> 1;
int M = -1;
for (int i = ql; i <= qr && i < mid; ++ i )
if (M == -1 || f[k][mid] > f[k - 1][i] + w[i + 1][mid]) {
f[k][mid] = f[k - 1][i] + w[i + 1][mid];
M = i;
}
solve(k, l, mid - 1, ql, M);
solve(k, mid + 1, r, M, qr);
}
void add(int x_0, int y_0, int x_1, int y_1) {
++ w[x_0][y_0];
-- w[x_0][y_1 + 1];
-- w[x_1 + 1][y_0];
++ w[x_1 + 1][y_1 + 1];
}
int solve() {
cin >> n >> k;
k ++ ;
for (int i = 1; i <= n; ++ i ) cin >> a[i];
for (int i = 0; i <= n; ++ i )
for (int j = 0; j <= n; ++ j ) {
w[i][j] = 0;
f[i][j] = 1e9;
}
for (int i = 1; i <= n; ++ i )
for (int j = i + 1; j <= n; ++ j )
if (a[i] > a[j]) {
add(1, j, i, n);
}
for (int i = 1; i <= n; ++ i )
for (int j = 1; j <= n; ++ j )
w[i][j] += w[i - 1][j] + w[i][j - 1] - w[i - 1][j - 1];
for (int i = 1; i <= n; ++ i ) f[1][i] = w[1][i];
for (int i = 2; i <= k; ++ i ) {
solve(i, 1, n, 0, n - 1);
}
return f[k][n] == 1e9 ? 0 : f[k][n];
}
int main() {
int T;
cin >> T;
while (T -- ) cout << solve() << '\n';
return 0;
}
```