概率与期望

· · 个人记录

零. 目录

一. 概率的理论

二. 概率的例题

三. 期望的理论

四. 期望的例题

五. 期望的特殊题型——后效性期望

一. 概率的理论

1.事件的概念

（1）样本点（单位事件）：

一个随机现象中可能发生的不能再细分的结果被称为样本点 或 单位事件。

（2）样本空间：

在随机试验中可能发生的所有单位事件的集合称为样本空间 或 事件空间。
通常用符号 \Omega 或大写字母 S 来表示样本空间。

（3）随机事件：

一个随机事件是样本空间 \Omega 的子集，它由若干样本点构成，用大写字母A, B, C, \cdots表示。
对于一个随机现象的结果 \omega 和一个随机事件 A，我们称事件 A 发生了当且仅当 \omega \in A。

例子：
在掷一次骰子的随机试验中，如果用掷出的点数作为单位事件，那么样本空间 \Omega=\{1,2,3,4,5,6\}。
设随机事件 A=\{5,2\}，如果某次掷骰子掷出了点数 6，由于 6\notin A，故事件 A 没有发生。

（4）事件域

定义略。常用记号 \mathcal{F} 表示。

2.事件的运算

可以将事件间的运算看作是集合间的计算，符号与集合间运算符号保持一致。
（1）和事件
相当于并集。对于事件 A 与 B 的和事件，记作 A+B 或 A\cup B。
（2）积事件
相当于交集。对于事件 A 与 B 的积事件，记作 A* B 或 AB 或 A\cap B。
（3）事件的包含
如果发生了 A 事件就一定发生了 B 事件，那么我们称事件 A 包含于 事件 B，记作 A\subseteq B。
（4）对立事件
对于事件 A 的对立事件，即事件 A 不发生也是一种事件，记作 \overline{A}。
（5）事件的差
相当于差集。对于事件 A 之于 B 的差事件，即 A 发生但 B 不发生也是一种事件，记作 A-B。
（6）事件的运算律
都可以将 + 视为 \cup，* 视为 \cap，按照集合间的运算去做即可。

$$A+B=B+A$$ $$A*B=B*A$$ $(II)$ 结合律 $$(A+B)+C=A+(B+C)$$ $$(A* B)* C=A* (B* C)$$ $(III)$ 分配律 $$A* (B+C)=(A* B) + (A* C)$$ $$A+(B* C)=(A+B)* (A+C)$$ $(IV)$ 对偶律 $$\overline{A+ B}=\overline{A}* \overline{B}$$ $$\overline{A* B}=\overline{A}+ \overline{B}$$ #### 3.概率的概念 （1）概率 > 设 $E$ 为随机试验，$\Omega$ 为它的样本空间。对于 $E$ 的每一个事件 $A$ 赋予了一个实数成为事件 $A$ 的概率，记为 $P(A)$。 （2）概率的性质 > $(I)$ 非负性 对于任意事件 $A$，都有 $0\le P(A)\le1$。 $(II)$ 规范性 对于样本空间 $\Omega$ 恒有 $P(\Omega)=1$。 $(III)$ 可数可加性 若一列事件 $A_1,A_2...$ **两两不交**，则 $P(\bigcup_{i\ge1}A_i)=\sum_{i\ge1}P(A_i)

（3）概率空间

我们将一个三元组 (\Omega , \mathcal{F} , P) 称为一个概率空间。

（4）古典试验与古典概率

如果一个试验满足两个条件：

$(II)$ 试验的每个基本结果出现的**可能性一样**。 那么我们就将这样的试验称为**古典试验**。 对于古典试验中的事件 $A$，它的概率定义为： $$P(A)=\dfrac{\#(A)}{\#(\Omega)}=\dfrac{m}{n}$$ 其中 $\#(\cdot)$ 表示对随机事件（一个集合）大小的度量， $n$ 表示该试验中所有可能出现的基本结果总数目，$m$ 表示事件 $A$ 包含的试验基本结果数。

4.概率的运算性质及事件的独立性

（1）广义加法公式

对于任意两个事件 A,B，都有：

P(A\cup B)=P(A)+P(B)-P(A\cap B)

本质上就是容斥。

（2）事件的独立性

若同一概率空间中的事件 A,B 满足：

P(AB)=P(A)P(B)

那么我们就称事件 A 和事件 B 是独立的。
对于多个事件 A_1,A_2,...A_n，我们称其独立的，当且仅当对于任意一组事件 \{A_{i_k}:1\le i_1<i_2<...<i_k\le n\}都有：

P(A_{i_1}A_{i_2}\cdots A_{i_r})=\prod_{k=1}^rP(A_{i_k})

文字表述即为：
一般地，设 A_1,A_2,\cdots ,A_n 是 n(n\ge 2) 个事件，如果对于其中任意 i(2\le i\le n) 个事件的积事件的概率，都等于各事件概率的乘积，则称 A_1,A_2,\cdots ,A_n 相互独立。

需要注意的是，多个事件相互独立一定能推出两两独立；
但多个事件两两独立不一定能推出相互独立。

例如： 有一个正四面体骰子，其中三面被分别涂成红色、绿色、蓝色，另一面则三色皆有。现在扔一次该骰子，令事件 A,B,C 分别表示与桌面接触的一面包含红色、绿色、蓝色。
不难计算 P(A)=P(B)=P(C)=\dfrac{1}{2}，P(AB)=P(BC)=P(CA)=P(ABC)=\dfrac{1}{4}。
显然 A,B,C 两两独立，但由于 P(ABC)\ne P(A)P(B)P(C)，故 A,B,C 不独立。

5.条件概率

（1）条件概率的定义

若已知事件 A 发生，在此条件下事件 B 发生的概率称为条件概率，记作 P(B|A)。
若 P(A)\ne 0，那么有：

P(B|A)=\dfrac{P(AB)}{P(A)}

（2）条件概率的乘法公式

P(AB)=P(A)P(B|A)=P(B)P(A|B)

（3）全概率公式

在概率空间(\Omega , \mathcal{F} , P)中若一组事件 A_1,A_2,\cdots ,A_n 两两不交且和为 \Omega（一组完备事件），则对于任意事件 B 有：

P(B)=\sum_{i=1}^nP(A_i)P(B|A_i)

证明：
由条件概率的乘法公式，有：

P(B)=\sum_{i=1}^nP(A_i)P(B|A_i)=\sum_{i=1}^nP(A_iB)

又因为A_1,A_2,\cdots ,A_n 两两不交且和为 \Omega，故 B 与所有 A_i 交起来即为 B 与 \Omega 交起来 即为 P(B)。
证毕。

这个公式告诉了我们，想要求一个事件 B 的概率 P(B)，可以求该概率空间中完备事件的概率 P(A_i) 以及条件概率 P(B|A_i)。

（4）Bayes 公式（贝叶斯公式）

对于一组完备事件 A_1,A_2,\cdots ,A_n，若 \forall i\in [1,n],P(A_i)>0，则：

P(A_i|B)=\dfrac{P(A_iB)}{P(B)}=\dfrac{P(A_i)P(B|A_i)}{\sum_{j=1}^n P(A_j)P(B|A_j)}

二. 概率的例题

有时间了再慢慢补。
不要急急国王。

三. 期望的理论

1.随机变量及其独立性

（1） 随机变量

高中选修三定义：
一般地，对于随机试验样本空间 \Omega 中的每个样本点 \omega，都有唯一的实数 X(\omega) 与之对应，我们称 X 为随机变量。

给定概率空间 $(\Omega,\mathcal{F},P)$，定义在样本空间 $\Omega$ 上的函数 $X:\Omega \to \mathbb{R}$ 若满足： 对于任意 $t\in \mathbb{R}$ 都有： $$\{\omega \in \Omega : X(\omega)\le t\}\in \mathcal{F}$$ 则称 $X$ 为**随机变量**。

（2） 离散型随机变量

可能取值为有限个或者有无限个取值，但可以一一列举出来（可列无穷大）的随机变量，我们称它为离散型随机变量。

（3） 分布列

一般地，设离散型随机变量 X 的可能取值为 x_1,x_2,\cdots x_n，我们称 X 取每一个值 x_i 的概率

P(X=x_i)=p_i,i=1,2,\cdots ,n

为 X 的概率分布列，简称分布列。

（4）随机变量的独立性

仿照事件的独立性中的定义：
若随机变量 X,Y 满足 P((X=x)\cap (Y=y))=P(X=x)P(Y=y) ，那么我们称这两个随机变量独立。
类似的，若多个随机变量相互独立，则两两独立。
若多个随机变量两两独立，它们不一定相互独立。

（Tips. 其实这里的定义是针对于离散型随机变量的，若涉及连续型随机变量，最正确的定义应该用连续函数定义，但这个不重要，暂不作讨论，感兴趣可以去 OI\ Wiki 上翻阅。）

（5）示性函数
对于样本空间 \Omega 上的事件 A，定义随机变量

1,&\omega\in A \\ 0,&\omega\notin A \end{matrix}\right.

称 I_A 是事件 A 的示性函数。

2.期望的概念

（Tips. 除特殊说明外，对于此处及本文中所有的期望均指代的是离散型随机变量的数学期望）。
一般地，对于离散型随机变量 X 的分布列 P(X=x_i)=p_i,i=1,2,\cdots ,n，我们称

E(X)=\sum_{i=1}^n x_ip_i

为随机变量 X 的 均值 或 数学期望，数学期望又简称 期望。

期望可以理解成是随机变量可能取值关于取值概率的加权平均数，它综合了随机变量的取值和取值的概率，反映了随机变量取值的平均水平。

3.期望的性质

（1）期望的线性性

性质1 对于随机变量 X 与任意实数 a,b，若随机变量 X 的期望存在，则：

E(aX+b)=aE(X)+b

证明：
先考虑证明 E(X+b)=E(X)+b。
根据离散型随机变量的期望的定义有：

E(X+b)&=\sum_{i=1}^n(x_i+b)p_i \\ &=\sum_{i=1}^nx_ip_i\ +\sum_{i=1}^nbp_i \\ &=\sum_{i=1}^nx_ip_i\ +b\sum_{i=1}^np_i \\ &=E(X)+b \end{aligned}

证明成立。

再考虑证明 E(aX)=aE(X)。
根据离散型随机变量的期望的定义有：

E(aX)&=\sum_{i=1}^nax_ip_i \\ &=a\sum_{i=1}^nx_ip_i \\ &=aE(X) \end{aligned}

证明成立。

因此，E(aX+b)=E(aX)+b=aE(X)+b
证毕。

性质2 对于任意两个离散型随机变量 X,Y，若其期望存在，则：

E(X+Y)=E(X)+E(Y)

证明：
（建议先将下面的条件期望和全期望公式阅读完后来看这个证明）
根据离散型随机变量的期望的定义有：

E(X+Y)&=\sum_{i=1}^n\sum_{j=1}^m(x_i+y_j)P((X=x_i)\cap (Y=y_j))\\ &=\sum_{j=1}^m\sum_{i=1}^nx_iP((X=x_i)\cap (Y=y_j))+\sum_{i=1}^n\sum_{j=1}^my_jP((X=x_i)\cap (Y=y_j))\\ &=\sum_{j=1}^m\sum_{i=1}^nP(Y=y_j)\dfrac{x_iP((X=x_i)\cap (Y=y_j))}{P(Y=y_j)}+\sum_{i=1}^n\sum_{j=1}^mP(X=x_i)\dfrac{y_jP((X=x_i)\cap (Y=y_j))}{P(X=x_i)}\\ &=\sum_{j=1}^mP(Y=y_j)\sum_{i=1}^n\dfrac{x_iP((X=x_i)\cap (Y=y_j))}{P(Y=y_j)}+\sum_{i=1}^nP(X=x_i)\sum_{j=1}^m\dfrac{y_jP((X=x_i)\cap (Y=y_j))}{P(X=x_i)}\\ &=\sum_{j=1}^mP(Y=y_j)E(X|(Y=y_j))+\sum_{i=1}^nP(X=x_i)E(Y|(X=x_i)) \end{aligned}

由全期望公式可知，\sum_{j=1}^mP(Y=y_j)E(X|(Y=y_j))=E(X)，\sum_{i=1}^nP(X=x_i)E(Y|(X=x_i))=E(Y)
故 E(X+Y)=E(X)+E(Y)。
证毕。
这个公式很常用，利用这个性质，可以将一个变量拆分成若干个变量，分别求这些变量的期望值，最后相加得到所求变量的期望值。

推论1 对于任一常数 a，有

E(a)=a

推论2

E(\sum_{i=1}^na_iX_i)=\sum_{i=1}^na_iE(X_i)

两个推论都比较显然，证明略去。

性质3 对于两个独立的离散型随机变量 X,Y，若其期望存在，则：

E(XY)=E(X)E(Y)

证明：
根据离散型随机变量的期望及其独立性的定义有：

E(XY)&=\sum_{i=1}^n\sum_{j=1}^mx_iy_jP((X=x_i)\cap(Y=y_j))\\ &=\sum_{i=1}^n\sum_{j=1}^mx_iy_jP(X=x_i)P(Y=y_j)\\ &=\sum_{i=1}^n\sum_{j=1}^mx_iy_jp_ip_j\\ &=\sum_{i=1}^nx_ip_i\sum_{j=1}^my_jp_j\\ &=E(X)E(Y) \end{aligned}

（2）期望的单调性

对于任意两个随机变量（包括连续型随机变量）X,Y，若 X\le Y，则 E(X)\le E(Y)，\ge也同理。
由于证明涉及密度函数上的不定积分，故此处不做讨论。

4.条件期望

（1）条件期望的定义

对于任意两个随机变量 X,Y，那么在已知条件 Y=y 下 X 的期望为此条件下 X 的条件期望，记作 E(X|Y=y)。
由定义易知：

E(X|Y=y)&=\sum_{i=1}^nx_iP(X=x_i|Y=y)\\ &=\sum_{i=1}^nx_i\dfrac{P((X=x_i)\cap (Y=y))}{P(Y=y)} \end{aligned}

（2）全期望公式

对于任意两个随机变量 X,Y，若其期望存在，则有：

E(X)=E(E(X|Y))=\sum_{i=1}^nE(X|(Y=y_i))P(Y=y_i)

给出一种不太严谨的证明：
根据条件期望的定义有：

E(E(X|Y))&=\sum_{i=1}^nE(X|Y=y_i)P(Y=y_i)\\ &=\sum_{i=1}^n\sum_{j=1}^m(x_j\dfrac{P((X=x_j)\cap (Y=y_i))}{P(Y=y_i)} )P(Y=y_i)\\ &=\sum_{i=1}^n\sum_{j=1}^mx_jP((X=x_j)\cap (Y=y_i))\\ &=\sum_{j=1}^m\sum_{i=1}^nx_jP((X=x_j)\cap (Y=y_i))\\ &=\sum_{j=1}^mx_j\sum_{i=1}^nP((X=x_j)\cap (Y=y_i))\\ &=\sum_{j=1}^mx_jP(X=x_j)\\ &=E(X) \end{aligned}

5.期望与概率的转化

对于随机事件 A，考虑其示性函数 I_A：

1,&\omega\in A \\ 0,&\omega\notin A \end{matrix}\right.

根据定义可以求得其期望 E(I_A)=P(A)。这一转化在实际应用中非常常见。

例子：假设对于一个长为 n 的序列 \{ a_i \}，其中 a_k 以 p_k 的概率取 k，以 1 - p_k 的概率取 0。考虑如何求 S = \sum_{i=1}^{n} a_i 的期望。
法一\quad 设 I_k 表示随机事件 a_k=k 的示性函数，则：

S=\sum_{k=1}^nkI_k

故：

E(S)&=E(\sum_{k=1}^nkI_k)\\ &=\sum_{k=1}^nkE(I_k)\\ &=\sum_{k=1}^nkp_k \end{aligned}

法二\quad 由期望的线性性及其定义可知：

E(S)&=E(\sum_{i=1}^na_i)\\ &=\sum_{i=1}^nE(a_i)\\ &=\sum_{i=1}^n(i\times p_i+0\times (1-p_i))\\ &=\sum_{i=1}^nip_i \end{aligned}

6.方差的定义

对于离散型随机变量 X 的分布列 P(X=x_i)=p_i,i=1,2,\cdots ,n，若期望 E(X) 存在，则我们称

D(X)=\sum_{i=1}^n(x_i-E(X))^2p_i=E((X-E(X))^2)

为随机变量 X 的方差，记作 D(X) 或 Var(X)。
特别地，我们将方差的算术平方根 \sigma(X)=\sqrt{D(X)} 称作随机变量 X 的标准差。

7.方差的性质

（1）方差定义式的等价式：

D(X)=E(X^2)-E^2(X)

证明：

D(X)&=E((X-E(X))^2)\\ &=E(X^2-2E(X)X+E^2(X))\\ &=E(X^2)-E(2E(X)\cdot X)+E(E^2(X))\\ &=E(X^2)-2E(X)E(X)+E^2(X)\\ &=E(X^2)-E^2(X) \end{aligned}

证毕。

这个玩意其实是跟选修三上的这个式子等价的：（从这可以知道 E(X^2) 的含义）

D(X)=\sum_{i=1}^nx_i^2p_i-E^2(X)

（2）方差的部分线性性

性质1 对于任意常数 a,b 与离散型随机变量 X，有：

D(aX+b)=a^2D(X)

证明：
先考虑证明 D(X+b)=D(X)。
根据方差的定义式有：

D(X+b)&=E(((X+b)-E(X+b))^2)\\ &=E(((X+b)-E(X)-b)^2)\\ &=E((X-E(X))^2)\\ &=D(X) \end{aligned}

证明成立。

再考虑证明 D(aX)=a^2D(X)。
根据方差定义式的等价式有：

D(aX)&=E((aX)^2)-E^2(aX)\\ &=a^2E(X^2)-E(aX)\cdot E(aX)\\ &=a^2E(X^2)-aE(X)\cdot aE(X)\\ &=a^2(E(X^2)-E^2(X))\\ &=a^2D(X) \end{aligned}

证明成立。

因此，D(aX+b)=D(aX)=a^2D(X)。
证毕。

性质2 若离散型随机变量 X,Y 独立，则：

D(X+Y)=D(X)+D(Y)

证明：
根据方差定义式的等价式有：

D(X+Y)&=E((X+Y)^2)-E^2(X+Y)\\ &=E(X^2+2XY+Y^2)-(E(X)+E(Y))^2\\ &=E(X^2)+E(Y^2)+E(2XY)-E^2(X)-E^2(Y)-2E(X)E(Y)\\ &=(E(X^2)-E^2(X))+(E(Y^2)-E^2(Y))+E(2XY)-2E(X)E(Y)\\ &=(E(X^2)-E^2(X))+(E(Y^2)-E^2(Y))+2E(XY)-2E(X)E(Y)\\ &=(E(X^2)-E^2(X))+(E(Y^2)-E^2(Y))+2E(X)E(Y)-2E(X)E(Y)\\ &=D(X)+D(Y)+0\\ &=D(X)+D(Y) \end{aligned}

证毕。

（3）其它性质

对于离散型随机变量 X 以及常数 c，有：

D(X)\le E((X-c)^2)

证明：
令函数 f(c)=E((X-c)^2)=E(X^2)-2cE(X)+c^2。
可以看出 f(c) 是凹函数。
对其求导有：

故当 $f'(c)=2c-2E(X)=0$ 即 $c=E(X)$ 时 $g(c)$ 取得最小值。 故 $D(X)=E((X-E(X))^2)\le E((X-c)^2)

四. 期望的例题

前言：题目有点小多，就只点出关键思路，些许直言片语耳。

例题 1 Shooting Gallery
假期望，真 dp。
由期望的线性性告诉我们，可以分别计算每一个靶子得分的期望。
而每一个靶子得分的期望为 1\times p_i+0\times (1-p_i)=p_i。
所以题目的意思便是让你求能击中的靶子概率总和最大是多少。
一眼 dp。
设 dp[i] 表示只考虑前 i 个靶子，能击中的最大概率总和。
发现不好转移，第 i 个靶子能否被打击会取决于上一个被打击的靶子。
所以改变 dp 状态，将后效性去掉。
设 dp[i] 表示按照时间排序后只考虑前 i 个靶子，且第 i 个靶子必须打击的最大概率总和。
由于对时间排了序，且题干中也说了第 k 个靶子在 t_k 秒出现并立刻消失，
所以这样设 dp 状态是正确的。
转移就简单了。

dp[i]=Max_{j<i,check(j,i)}\{dp[j]\}+p[i]

其中 check(j,i) 表示是否能从 j 靶子移动到 i 靶子，即 t[i]-t[j]\ge \sqrt{(x[i]-x[j])^2+(y[i]-y[j])^2}。
所以说这道题难在 dp。
时间复杂度 \mathcal{O}(n^2)。
code

例题 2 Second price auction
这道题还有点重要。
想直接求第二高价格期望？
做梦吧。
对于形如 第 k 大 的期望，常有这种转换：

将 第 k 大 \to 至少 k 个。

比如这道题。
设 p[i] 表示第二高出价恰好为 i 的概率。
那么答案就是 \sum_{x=minw}^{maxw}p[x]\times x。
考虑 p[i] 如何求。
恰好是不好求解的，所以使用上面提到的 Trick：

那么 $p[i]=f[i]-f[i+1]$。 所以现在重点便是如何求 $f[i]$ 了。 设 $dp[i][j]$ 表示前 $i$ 个人中**恰好**有 $j$ 个人**至少**出价 $x$ 的概率，枚举 $x$； 那么 $f[x]=\sum_{j=2}^ndp[n][j]$。 然后就只用考虑求 $dp$ 了。 $dp$ 的转移是显然的，分类讨论即可。 只是代码上细节可能有点多，其它就没什么了。 本题中同理可以求出第 $k$ 大出价的期望，只需要将 $f[x]=\sum_{j=k}^ndp[n][j]$ 即可。 像是这种常见的 $Trick$ 还是多积累的好，建议反复食用。 时间复杂度 $\mathcal{O}(n^3)$。 [code](https://www.luogu.com.cn/paste/ditfl6qd) **例题 $3$** [Maxim and Restaurant](https://www.luogu.com.cn/problem/CF261B) 一拿到题感觉无从下手。 还是考虑从期望题常用技巧入手。 由期望的定义，想求期望，需要求出每种方案的进入人数和这种方案的概率。 不难知道每种方案的概率都是 $\dfrac{1}{n!}$。 所以问题便转化为了求**所有方案中能进入的人数总和**。 再次思考，发现关键在于那个**恰好到他就进不去的被“卡住”的人**。 所以考虑枚举被卡住的人 $x$。 设 $dp_x[i][j][k]$ 表示在 $x$ 是被卡住的人的前提下，前 $i$ 个人中选 $j$ 个人（组合意义）共占空间 $k$ 的方案数。 转移方程很显然，$dp_x[i][j][k]=dp[i-1][j][k]+dp[i-1][j-1][k-a[i]]$ 。 发现第一维可以滚动掉。 那么就是一个裸的 $dp$ 了。 初始状态 $dp_x[0][0][0]=1$。 唯一需要注意的点是，由于当前枚举的是第 $x$ 个人被卡住，所以当 $i=x$ 时转移应为 $dp_x[i][j][k]=dp_x[i-1][j][k]$。 然后再考虑满足第 $x$ 个人恰好卡住的方案中的总人数。 不难得知，对于第 $x$ 个人前面进去了的人所占的空间 $k$ 要满足： $$p\ge k,k+a[x]> p\Rightarrow p\ge k\ge p-a[x]+1$$ 枚举前面进去的人数 $j$，由于第 $x$ 个人能否进去和前面 $j$ 个人的进入顺序无关，故还要乘上排列数 $j!\times (n-j-1)!

因此，答案为：

ans=\dfrac{\sum_{x=1}^n \sum_{j=1}^{n-1}\sum_{k=max(p-a[x]+1,0)}^p j\times (dp_x[n][j][k]\times j!\times (n-j-1)!)}{n!}

注意每次枚举 x 时 dp 都要清空重算。
交上去后发现 WA 了一个点。
发现当 sum_a\le p 即所有人都能进去时转移会出错。
这种情况特判就行了。
时间复杂度 \mathcal{O}(n^4)。
code

例题 4 Random Query
水题。
套路化地，将期望拆开，分别计算每一个位置对答案的贡献。
易知当 l\neq r 时选到每一个区间的概率都是 \dfrac{2}{n^2}。
而当 l=r 时选到的每一个区间的概率都是 \dfrac{1}{n^2}。
为了方便，默认所有区间的概率都是 \dfrac{2}{n^2}，统计答案时只需要将所有 l=r 的区间减去 \dfrac{1}{n^2} 即可。
概率知道了，考虑贡献。
直接去看区间的贡献是 \mathcal{O}(n^2) 的，无法通过本题。
所以考虑每个位置对答案的贡献，只需要看哪些区间包含了这个位置的贡献即可，那么就是 O(n) 的，可以通过。
对于一个区间内一个数字出现了多个，我们只考虑它最左边的那个数字的贡献。
记数字 x 上一次出现的位置为 pre[x]。
那么对于位置 i 上的数字 a[i]，当且仅当一个区间 [l,r] 满足 pre[a[i]]<l\le i\le r\le n 时 i 上的数字对这个区间有 1 的贡献。
那么对于位置 i 对答案的贡献就应该是 \dfrac{2\times (i-pre[a[i]])\times (n-i+1)}{n^2}。
最后减去多余贡献 \dfrac{n}{n^2}=\dfrac{1}{n} 即可。
即：

ans=-\dfrac{1}{n}+\sum_{i=1}^n \dfrac{2\times (i-pre[a[i]])\times (n-i+1)}{n^2} [code](https://www.luogu.com.cn/paste/nw0cl1hi) **例题 $5$** [Let's Play Osu!](https://www.luogu.com.cn/problem/CF235B) ~~音游人狂喜。~~ 两句话概括题意：有 $n$ 个字符，第 $i$ 个字符有 $p_i$ 的概率是 ‘$O$’，$1-p_i$的概率是 ‘$X$’。总得分为每一连续极大 ‘$O$’ 段的长度平方之和，求得分的期望。 拿到题没思路？ 还是按照期望题的套路来。 首先总的期望直接求不好求，怎么办？ 拆开统计每一位的贡献。 每一位的贡献怎么求？ 期望 $dp$。 $dp$ 状态怎么设才没问题？ > **一个小技巧： 在期望$dp$ 中，常常将 $dp$ 状态设为从 $1$ ~ $i$ 或者是从 $i$ ~ $n$ 的某结果。 如果有后效性，为了避免后效性，常强制性令 $i$ 必选。** 这个 $Trick$ 在期望 $dp$ 中很常用，比如本题和后面的例题 $7$。 回到本题上，沿用上述 $Trick$，设 $dp[i]$ 表示以 $i$ 结尾的连续段 ‘$O$’ 期望长度。 所以只需要考虑前 $i$ 位且只用考虑含 $i$ 的这一段。 先考虑如果已知 $dp[i]$ 如何求答案。 为方便起见，设 $s[i]$ 表示第 $i$ 位对答案的得分贡献。 这时有些同学（~~比如我~~）可能就会想着哎这还不好求，这不就是 $dp[i]^2\times p[i]$ 吗？ 然鹅当你将样例带进去算时你会发现样例都是错的$\cdots\cdots$ 你发现答案远小于正确答案。 问题在哪？ 问题就在于**不能对均值平方得到平方的均值**，即 $E^2(X)\ne E(X^2)$。 由于期望 $E$ 本身衡量的便是长度的均值，本来正确的得分期望应该是每种长度的平方乘上相应的概率再求和。 而你直接平方去算的话就相当于是先将长度取了均值后再平方，答案是不一样的。 举个栗子： 比如 $n=2$，考虑 $s[2]$。 假设每个字符的概率都为 $p_i=0.5$。 发现 $s[2]$ 只有两种情况： "$XO$" 或 "$OO$"。两种情况的概率均为 $0.25$。 正确的做法应是 $s[2]=1^2\times 0.25+2^2 \times 0.25=1.25

而错误的做法是

那么该如何求 $s[i]$？ **整体考虑**。 由于第 $i$ 位必须是 ‘$O$’ （若不是的话这一段的贡献就是 $0$ ，不需要考虑）， 那么 $s[i]$ 之于 $s[i-1]$ 而言相当于是**第 $i-1$ 位往左的所有含第 $i-1$ 位的连续段长度全部 $+1$** 。 而对于长度由 $x\to x+1$，得分会变化 $(x+1)^2-x^2=2x+1$。 而由于 $i-1$ 的所有长度的都会加 $1$，所以整体的期望得分就会增加 $2dp[i-1]+1$。（注意：这里直接用 $dp[i-1]$ 是因为 $2x-1$ 是线性的所以才可以，不然是不行的。） 即 $s[i]=p[i]\times (2dp[i-1]+1)$。**（还要乘上 $p[i]$ 是因为第 $i$ 位得是 ‘$O$’ 才有贡献）**。 因此答案便是 $\sum_{i=1}^np[i]\times (2dp[i-1]+1)$。 ~~桥豆麻袋~~ $dp$ 还没求呢！ 其实 $dp$ 转移是最简单的。 由于第 $i$ 位必须是 ‘$O$’，所以不难得知 $dp[i]=p[i]\times (dp[i-1]+1)$。 时间复杂度 $\mathcal{O}(n)$。 [code](https://www.luogu.com.cn/paste/8sxtwddo) 还没完。 > 拓展：[「BZOJ4318」OSU!](https://www.luogu.com.cn/problem/P1654) 这道题上面这道几乎一样，只不过将得分从 平方 变为了 三次方。 沿用上述套路，设 $dp[i]$ 表示以 $i$ 结尾的连续段 ‘$O$’ 期望长度，$s[i]$ 表示第 $i$ 位对答案的得分贡献。 还是考虑长度从 $i$ 变为 $i+1$ 对得分的贡献，$\Delta=(i+1)^3-i^3=3i^2+3i+1$。 重点来了，这里出现了平方项，怎么办？ **令 $x=i^2$，那么 $3i^2=3x$ 就是线性的了**。 换句话说，**要分别维护长度的期望和长度的平方的期望**。 长度的期望和上面一样，$dp_1[i]=p_i\times(dp_1[i-1]+1)$。 长度平方的期望和长度的期望求法是一样的，$dp_2[i]=p_i\times (dp_2[i-1]+1)^2$。 真的是这样吗？ 成功地连样例都过不了。 为什么呢？ 还是那句老话，**$E(X^2)\ne E^2(X)$ ！！！** 长度 $+1$ 后，长度的期望确实是加了 $1$，但长度的平方呢？ 应为 $(dp[i]+1)^2=dp_2[i]+2dp_1[i]+1$。 因此，$dp_2[i]=p_i\times (dp_2[i-1]+2dp_1[i-1]+1)$。 这一点**尤其注意**。 怎样做才不易出错呢？ 介绍一种**不容易出错的通用方法**： 设离散型随机变量 $X_i$ 表示以 $i$ 结尾的连续段 ‘$O$’ 的期望长度，$s_i$表示第 $i$ 位的得分期望，那么： $$s_i=p_i\times (E((X_{i-1}+1)^3)-E(X_{i-1}^3))=p_i\times(3E(X_{i-1}^2)+3E(X_{i-1})+1)$$ > **分别维护** $E(X^2)$ 和 $E(X)$。 $X_i=X_{i-1}+1$，故 $E(X_i)=p_i\times (E(X_{i-1})+1)$； $X_i^2=(X_{i-1}+1)^2=X_{i-1}^2+2X_{i-1}+1$，故 $E(X_i^2)=p_i\times E(X_{i-1}^2+2X_{i-1}+1)=p_i\times(E(X_{i-1}^2)+2E(X_{i-1})+1)$。 答案即为 $\sum_{i=1}^n p_i\times(3E(X_{i-1}^2)+3E(X_{i-1})+1)$。 即 $\sum_{i=1}^n p_i\times (3dp_2[i-1]+3dp_1[i-1]+1)$。 这种思想可以扩展到任意次数。 ~~所以可以自己出一道拓展后的题了？~~ [code](https://www.luogu.com.cn/paste/j210op8r) （后记：我不知道这道题我有没有讲清楚，写得有点乱。 乱是因为写着写着就会产生新的疑惑，等想明白后就写上来，相当于呈现了我的思路历程，所以写的有点冗长。 希望能多消化消化尽量弄清楚吧。） （后后记：自己的题出出来了：[清夏？乐园？大秘境！](https://www.luogu.com.cn/problem/U317301)） **例题 $6$** [Third Month Insanity](https://www.luogu.com.cn/problem/CF859D) 期望 $dp$ 与树 $dp$ 结合的好题。 不难发现，比赛过程是一颗**满二叉树**。 出于习惯，不妨令 $1$ 和 $2$，$3$ 和 $4\cdots 2^{n-1}$ 和 $2^n$ 比赛。 考虑在二叉树上统计答案。 同样将期望拆开到每一个节点上，也就是说，只需要求出每一个节点上的最大期望。 而要求出每一个节点上的最大期望需要知道猜对的概率和所得分值。 所得分值很好求，即为 $2^{i-1}=$ $\dfrac{r-l+1}{2}$，其中 $l,r$ 当前节点的区间。 那就只需要求猜对的概率了。 明显的树上 $dp$。 设 $g[u][i]$ 表示子树 $u$ 内 $i$ 胜出的概率，$f[u][i]$ 表示 $g[u][i]$ 状态下的最大期望。 那么 $g[u][i]$ 就是节点 $u$ 猜对的概率了。 正确性很显然，因为你的猜测覆盖了所有的合法情况。 转移方程也不难写出。 $g[u][i]$ 的转移显然，枚举获胜者 $i$ 和它的对手 $j$ 即可： $$\sum_{i=l}^{mid}g[u][i] =\sum_{j=mid+1}^r g[u<<1][i]\times g[u<<1|1][j]\times p[i][j]$$ $$\sum_{i=mid+1}^{r}g[u][i] =\sum_{j=l}^{mid} g[u<<1|1][i]\times g[u<<1][j]\times p[i][j]$$ 至于 $f[u][i]$ 的转移，同样是枚举猜测的获胜者 $i$，但要注意，要将所有与 $i$ 对战的对手的期望加上取 $Max$： $$\sum_{i=l}^{mid}f[u][i]=Max_{j=mid+1}^r\{f[u][i],\dfrac{r-l+1}{2}\times g[u][i]+f[u<<1][i]+f[u<<1|1][j]\}$$ $$\sum_{i=mid+1}^{r}f[u][i]=Max_{j=l}^{mid}\{f[u][i],\dfrac{r-l+1}{2}\times g[u][i]+f[u<<1|1][i]+f[u<<1][j]\}$$ 由于不知道最终谁获胜，故最终的答案就是在根节点处取最大值： $$ans=Max_{i=1}^n f[1][i]$$ 时间复杂度 $\mathcal{O}(n4^n)$。 [code](https://www.luogu.com.cn/paste/9bv6m5i1) **例题 $7$** [Beautiful Mirrors](https://www.luogu.com.cn/problem/CF1265E) 一道非常经典的**可列无穷大**类型的期望 $dp$，建议反复食用。 还记得例题 $5$ 中提到的 $Trick$ 吗？ 直接求一头雾水，想 $dp$ 无从下手。 那，不妨先套路化地写个 $dp$ 状态出来再进行修改？ 设 $dp[i]$ 表示问到第 $i$ 面镜子的期望天数。 发现这里有歧义，因为第 $i$ 面镜子可能问到多次，所以修改一下 $dp$ 状态。 设 $dp[i]$ 表示**第一次**问到第 $i$ 面镜子且第 $i$ 面镜子回答“美”的期望天数。 其实这里就充分体现了那个 $Trick$：从 $1$ ~ $i$ 镜子都回答“美”的期望天数。 然后可列无穷大的 $dp$ 式子就很套路化了，需要理解透彻。 对于第 $i$ 面镜子： 如果它回答“美”，那么概率是 $p_i$，期望天数是 $dp[i-1]+1$； 如果它回答“不美”，那么概率是 $1-p_i$，期望天数是 $dp[i-1]+1+dp[i]$（这里便是这道题的**关键所在**）。 所以，转移方程为：$dp[i]=p_i\times (dp[i-1]+1)+(1-p_i)\times (dp[i-1]+1+dp[i])$。 化简后可得到真正的转移方程： $$dp[i]=\dfrac{dp[i-1]+1}{p_i}$$ 答案即为 $dp[n]$。 时间复杂度 $\mathcal{O(n)}$。 还有一点要注意的是： 结果要对分式取模。 >**分数取模**： 比如对于 $\dfrac{a}{b}(mod\ p,p\in prime)$，其中 $prime$ 表示质数集。 那么这个式子就等价于 $a\times inv(b)=a\times b^{p-2}$，其中 $inv$ 是逆元。 原理便是费马小定理。 之后很多题也有这个注意点，不再赘述。 [code](https://www.luogu.com.cn/paste/i3ucfomo) **例题 $8$** [Wish I Knew How to Sort](https://www.luogu.com.cn/problem/CF1753C) 前言：这道题难度感觉有点......因人而异？ 先不谈正解，先看看我刚开始是怎么做的。 设 $f[i][0/1]$ 表示第 $i$ 位是 $0$ 最终应该为 $0/1$ 的期望操作数，$g[i][0/1]$ 表示第 $i$ 位是 $1$ 最终应该为 $0/1$ 的期望操作数。 那么 $f[i][0]=\dfrac{1}{n}(g[i][0]+1),f[i][1]=\dfrac{1}{n}(g[i][1]+1)+\dfrac{n-1}{n}(f[i][1]+1)

同理 g[i][1]=\dfrac{1}{n}(f[i][1]+1),g[i][0]=\dfrac{1}{n}(f[i][0]+1)+\dfrac{n-1}{n}(g[i][0]+1)
然后进行化简，最终有：

f[i][0]=\dfrac{n+1}{n-1},g[i][0]=\dfrac{n^2+1}{n-1} 然后发现样例一个都过不去。 错在何处？ 错便错在了只考虑了一边。 当交换两个数字时，对两边都会有影响，且有后效性。 我这样考虑相当于是对第 $i$ 位异或 $1$ ，而非交换两个位置。 有后效性怎么办？ **整体考虑**。 考虑最终的序列会长成什么样子。 举个例子： 对于序列 $0\ 1\ 1\ 0\ 0\ 1$，最终序列应该为 $0\ 0\ 0\ 1\ 1\ 1$。 可以看出实际上就是要将左边的 $1$ 全部移到右边，右边的 $0$ 全部移到左边。 设这个序列中 $0$ 的数量为 $cnt_0$，那么可以发现： 对于一个交换 $(l,r)$，**当且仅当 $l\in[1,cnt0]$ 且 $a[l]=1,a[r]=0$ 时这个交换才是有用的**。 这条性质不难看出，但很关键。 如果在 $[1,cnt0]$ 或 $[cnt0+1,n]$ 内部交换不会对结果做出任何贡献，单单是增加了操作次数。 如果 $1\le l\le cnt0,cnt0+1\le r\le n $，不管 $a[l]$ 和 $a[r]$ 是什么，由题目，都会交换失败，也不会对结果做出任何贡献，单单是增加了操作次数。 所以考虑**将 $[1,cnt0]$ 内的 $1$ 的个数作为状态**。 设 $dp[k]$ 表示 $[1,cnt0]$ 内的 $1$ 的个数为 $k$，要将它变为 $dp[0]$（排好序）的期望操作次数。 显然 $dp[0]=0$。 考虑转移。 正着想不好想，所以倒着考虑。 考虑如何将 $dp[k]$ 转移到 $dp[k-1]$。 容易发现的是，如果 $[1,cnt0]$ 中有 $k$ 个 $1$，那么 $[cnt0+1,n]$ 中就有 $k$ 个 $0$。 总选择的方案数为 $C_n^2=\dfrac{n(n-1)}{2}$，对于所有方案分类进行讨论： 如果该选择是有效选择，即 $a[l]=1,a[r]=0$，那么概率是 $\dfrac{k^2}{(\dfrac{n(n-1)}{2})}=\dfrac{2k^2}{n(n-1)}$，期望步数是 $1+dp[k-1]$； 如果该选择是无效选择，那么概率是 $1-\dfrac{k^2}{(\dfrac{n(n-1)}{2})}=1-\dfrac{2k^2}{n(n-1)}$，期望步数是 $1+dp[k]$。 因此，转移方程式为： $$dp[i]=\dfrac{2k^2}{n(n-1)}(1+dp[k-1])+(1-\dfrac{2k^2}{n(n-1)})(1+dp[k])$$ 最后化简可得到真正的转移方程式： $$dp[i]=dp[i-1]+\dfrac{n(n-1)}{2k^2}$$ 设 $[1,cnt0]$ 中有 $cnt1$ 个 $1$，那么答案即为 $dp[cnt1]$。 这个式子就可以直接算了，但如果题目数据范围很大，内存不够的话可以将这个递推式展开。 由于 $dp[0]=0$，故展开后的结果为： $$ans=\sum_{i=1}^{cnt1}\dfrac{n(n-1)}{2i^2}$$ 不管展不展开，时间复杂度均为 $\mathcal{O}(n)$。 还有一点要注意，这道题数据很大，很容易爆 $long\ long$，在 $quick\_pow$ 函数中建议一来便将底数 $x$ 和指数 $k$ 取模。 就是因为我没有在这额外取模，导致一直 $WA$。 只能说，能取模的地方就尽可能地取模。 [code](https://www.luogu.com.cn/paste/4yjo6wlh) **** 总结： 期望的题目从以下方面思考： 1. 由期望的定义，**转换成概率或着是具体的数值和**。 2. 由期望的线性性**拆开**求，最后合在一起。 3. 常与**期望 $dp$，概率 $dp$** 等挂钩，多往这方面考虑。 **** ### 五. 期望的特殊题型——后效性期望 以一道例题引入： > 给定一颗 $n$ 个节点的树，每次操作等概率的选择一个点将它和它的子树全部从树上删掉，求删完整棵树的操作次数的期望值。（$n$ 很大） - 穿过烟帷与暗林： 初步思考后，不难发现这类题与上述四中的传统期望题的区别： 其富有**后效性**。 换句话说，每一次的操作都对之后的选择有影响，后面的操作依托于前面的操作。 当一个点被删去后，其子树内的点在之后的操作中就没法被选中删去了。 这就是所谓的**后效性期望**。~~（名字我瞎取的）~~ - 进一步深入： 直接考虑删掉哪一个点然后考虑对后面操作的影响显然是困难的，想了老久也没能想出来。 怎样避免思考后效性呢？ 考虑一个点**怎样出现在操作序列中**。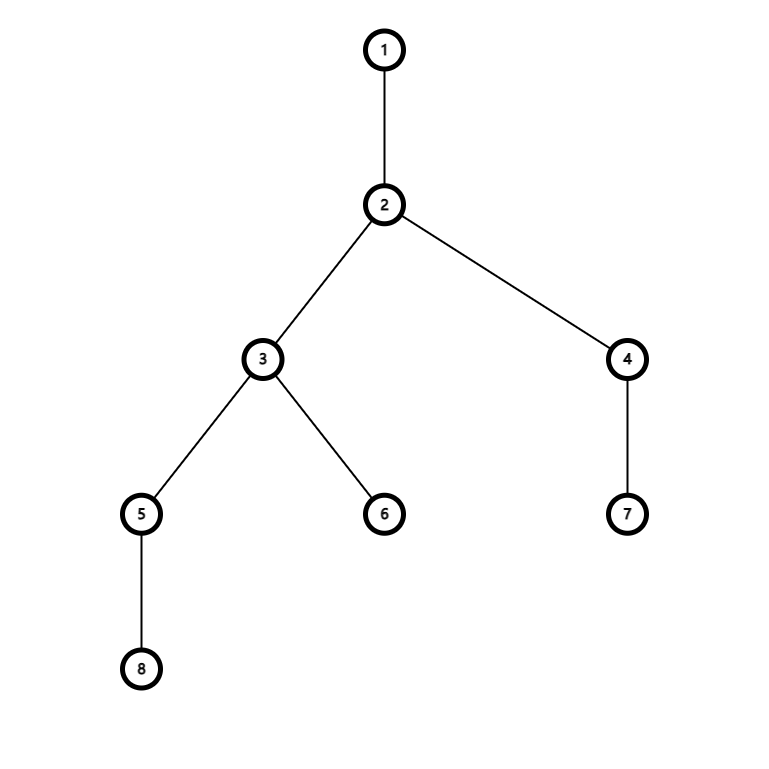 如下图： ![](https://cdn.luogu.com.cn/upload/image_hosting/w32olmxb.png) 比如要让点 $5$ 出现在操作序列里面。 不难发现删 $5$ 子树里的点对其是没有影响的。 而删其兄弟节点等也是没有影响的。 **只有当删掉它到根路径上的点会对它在操作序列中的出现有影响**。 所以考虑 $5\to 1$ 路径上的节点的删点顺序。 先不考虑这些点能不能被删除，先写一组操作序列如： $2,3,5,1

然后再将其中不合法的操作删去就会得到合法的一组操作序列：

2,1

发现 5 没有出现在操作序列中。
再写一组操作序列：

5,1,2,3

然后重复上述操作，得到的合法操作序列为：

5,1

发现 5 出现在了操作序列中。
看出规律了吗？
一般地，如果想让某个点 i 出现在操作序列中， 只有当操作序列的开头是这个点，后面任意时，这个点才会出现在操作序列中。
而在这段操作序列中，以点 i 开头的操作序列占总的 \dfrac{1}{deep[i]}。 （deep[1]=1）
而 5 若出现在操作序列中，则会对操作次数贡献 1\times \dfrac{1}{deep[i]}=\dfrac{1}{deep[i]}。
故 E(i)=\dfrac{1}{deep[i]}+0\times (1-\dfrac{1}{deep[i]})=\dfrac{1}{deep[i]}。
因此由期望的线性性可知：

ans=\sum_{i=1}^n \dfrac{1}{deep[i]}

然后我们就巧妙地解决了这道题。

类似的套路，如果上面的例题明白了，那么这道题也应该不难了。

ans=\sum_{i=1}^n \dfrac{1}{size[i]}

其实这道题可以改一改：
“每次操作等概率的选择一个白点将它到根路径上的所有点染成黑色” 改为
“每次操作等概率的选择一个白点和一个黑点将它们之间的最短路径上的所有点染成黑色”
答案还是一样的。