曲线系
Querainy
·
·
个人记录
把之前的删了,都放一块吧(
蝴蝶定理
这个是非常经典的问题对吧!但是我查到的好像都不是很能讲的明白,所以还是自己处理一下这个问题。
圆O,取任意弦AB,其中点C,再取过C的任意两条弦DE,FG,记EF,DG分别交AB于P,Q,则蝴蝶定理断言C是PQ中点。
我们以C为原点,BA为x轴正方向建系,设\odot O: x^2+(y-y_0)^2=r^2,DE:y-k_1x=0,FG:y-k_2x=0,那么我们断言\odot O+\lambda DE\cdot FG就是所有过D,E,F,G的二次曲线(除了DE\cdot FG)。由于直线对(EF,DG)也是二次曲线,所以必然有一个\lambda使得这个方程表示这个直线对,所以此时我们代入y=0就得到P,Q。整理得到(1+\lambda k_1k_2)x^2+y_0^2-r^2=0。然后使用韦达定理,这两个点横坐标之和是0,所以它们的中点就是C。
为什么这就是所有过D,E,F,G的二次曲线了??哎呀这个我不会证啊。
不过我们也可以证明一个更弱的结论,存在一个\lambda表示直线对(EF,DG),这对这个题就够用了。我们只需证明存在一个\lambda使得(1+\lambda k_1k_2)x^2+y_0^2-r^2=0的一个根是x_P,那么既然它过五个点就确定了一个二次曲线,而我们可以画出一个二次曲线,也就是直线对(EF,DG),它就必然是那个被确定的了啦。然后它是x^2=\frac{r^2-y_0^2}{1+\lambda k_1k_2},显然下面我们可以随便调,所以就结束了。
经典问题
这题是我们数学老师不知道从哪找的,本来是任意抛物线的,但是因为抛物线都相似所以没锤子用嘛。
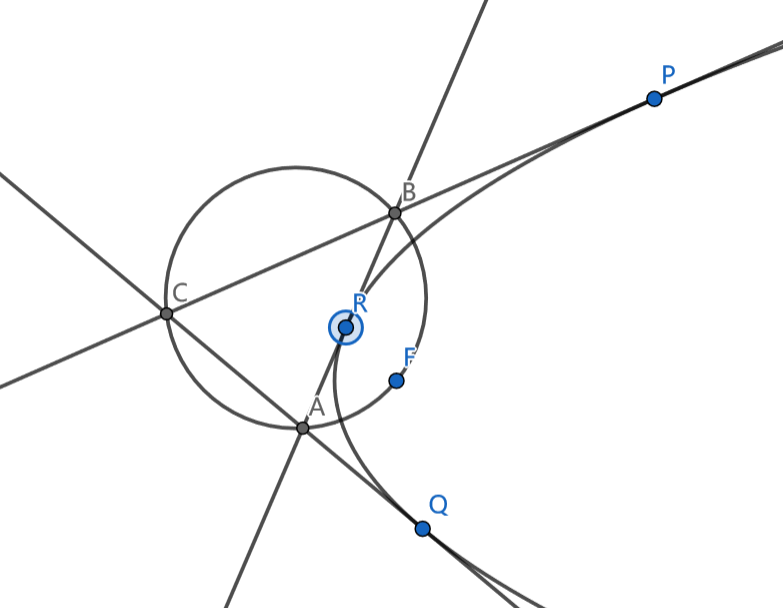
设$P(p^2,2p),Q(q^2,2q),R(r^2,2r)$,那么$BC:py-x-p^2=0,AB:ry-x-r^2=0,AC:qy-x-q^2=0$。我们直接算出这个圆,根据曲线系的结论必然存在$a,b,c$满足圆是$aAB\cdot AC+bAB\cdot BC+cAC\cdot BC$,不过我们不会这么说,我们会先猜存在然后算出$a,b,c$对吧。
我们知道如果它是圆那么必然能写成$(x-x_0)^2+(y-y_0)^2-k^2=0$的形式(这也是为啥我们齐次地设了$a,b,c$而非$1,\frac{b}{a},\frac{c}{a}$,如果是后一种设法$x^2$的系数就不一定是$1$了,所以前一种比较好看),所以开始狂暴比对系数,不过这里只有两个变量$\lambda,\mu$所以肯定很多等价的条件对吧。我们尽量不引入更多变量,所以先不管那些带$x_0,y_0,k$的项。看$x^2$项,我们得到$a+b+c=1$。$y^2$项是$aqr+bpr+cpq=1$。交叉项是$a(q+r)+b(p+r)+c(p+q)=0$,这样已经可以解了。虽然我用了wolframalpha,但是还是解得$a=\frac{1+p^2}{(p-q)(p-r)},b=-\frac{1+q^2}{(p-q)(q-r)},c=\frac{1+r^2}{(p-r)(q-r)}$。哎这个题真不是人算的......
然后说明$F$在圆上,代入$F(1,0)$,得$a(1+q^2)(1+r^2)+b(1+p^2)(1+r^2)+c(1+p^2)(1+q^2)=\frac{(1+p^2)(1+q^2)(1+r^2)((q-r)-(p-r)+(p-q))}{(p-q)(p-r)(q-r)}=0$,这就结束了。实际上这一步应该先做以观察目标的性质,比如蝴蝶定理那里根本不需要算出这几个参数。
看起来曲线系技巧多数时候只是让我们表示各种东西的时候更直接一点,比如这里就是不需要先算出点来再插出圆来,而可以直接这么表示圆对吧,然后下一个题是不需要算出点再插直线这样的。然后其实也不太需要用什么结论,因为你都解出来了嘛,说明它是圆(没有交叉项并且平方项系数都为$1$)并且过这三个点(从构造的曲线系方程可以直接看出)就好啦!
题外话:推荐阅读 https://zhuanlan.zhihu.com/p/680226805 ,感觉很有水平。
-----
另一个经典问题
(17全国I) 椭圆$C:\frac{x^2}{4}+y^2=1$及其上的$P(0,1)$,证明若直线$AB$交椭圆于$A,B$,且$PA,PB$斜率和为$-1$,则$AB$过定点。
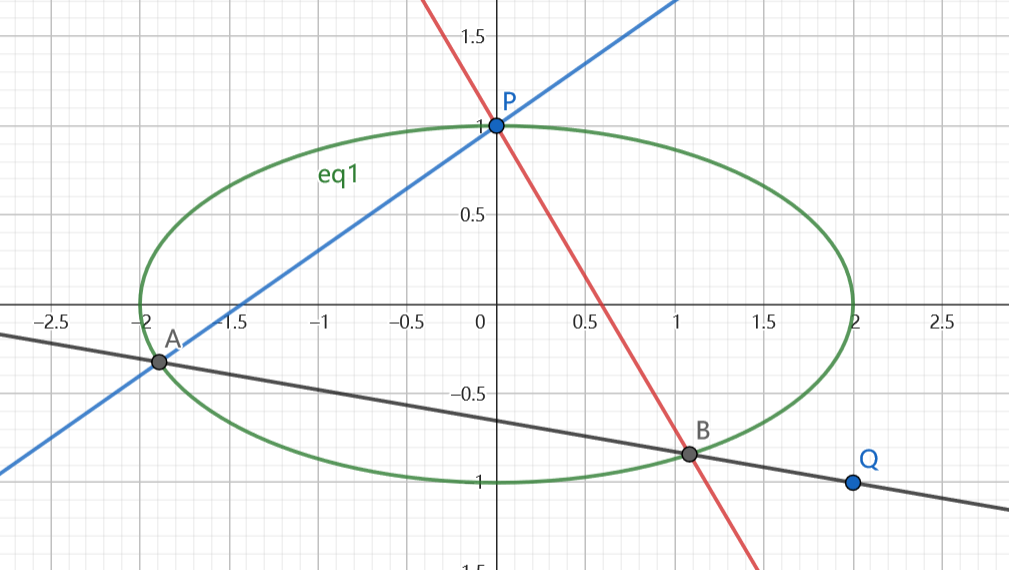
其中$Q(2,-1)$是那个定点。
设$PA:y-kx-1=0,PB:y+(k+1)x-1=0$,我们要凑出$AB$本身是不太可能的,因为消不掉所有二次项系数。还是考虑$4C+\lambda PA\cdot PB=(1-\lambda k(k+1))x^2+(\lambda+4)y^2+\lambda xy-\lambda x-2\lambda y+\lambda-4$,$A,B,P$满足这个方程,但是好像我们有点亏的,因为这里$P$出现了两次,但是关系不大,有结论是必然存在一个$\lambda$给出$(y-1)(y+mx+n)=0$,$y-1=0$是$P$处的切线,正如偶重根给出切线,这个嗯猜也能猜到对吧!!
为了证明它还是把它算出来,反正这个题本来就要把它算出来,我们要消去$x^2$项的系数,那么取$\lambda=\frac{1}{k(k+1)}$,得到$(\lambda+4)y^2+\lambda xy-\lambda x-2\lambda y+4\lambda-4=0\Leftrightarrow y^2+\frac{\lambda}{\lambda+4} xy-\frac{\lambda}{\lambda+4} x-\frac{2\lambda}{\lambda+4} y+\frac{\lambda-4}{\lambda+4}=0$,可以注意到所有$k$都消掉了,那么既然$\lambda$比较任意的所以就保留它而不要$k$好了。我们已经猜出可以分解为$(y-1)(y+mx+n)$,解得$m=\frac{\lambda}{\lambda+4},n=\frac{4-\lambda}{\lambda+4}$。那么由于这个式子是二次的,它过$P,A,B$,$y-1=0$只过$P$,所以$y+mx+n=0$必然过$A,B$,那么算一下$(\lambda+4)y+\lambda x+4-\lambda=0$过的定点就是$(2,-1)$。
-----
可能持续更新。