平衡树学习笔记
cppcppcpp3
·
·
算法·理论
引入
平衡树是一类支持高效进行以下操作的数据结构:
- 插入/删除一个数 x。
- 查询 x 的排名。
- 查询 x 的前驱/后继(最大的小于它的数/最小的大于它的数)
- 快速合并/分裂。
- 区间修改/查询/翻转。
- 维护其他信息。
前置:二叉搜索树
定义:二叉搜索树(BST)是一种二叉树的数据结构,每个节点都有一个附加权值,满足对于任何一棵子树,左子树所有点的权值小于根节点的权值,右子树所有点的权值都大于根节点的权值。
BST 的遍历:对 BST 进行中序遍历,得到的权值序列是非降序列,时间复杂度 O(n)。
时间复杂度:BST 上的基本操作的时间复杂度为 O(h),其中 h 表示树高。随机构造一棵 BST 的树高期望为 O(\log n)。当权值序列非降时,依次插入构造出的 BST 树就是一条链,树的高度达到最大,对应最坏复杂度 O(n)。
为了保证优秀的时间复杂度,我们需要使用一些手段维持树高(树的平衡性),由此引出各种平衡树。反过来看即平衡树满足 BST 的一切性质。下面介绍三种平衡树:替罪羊树、旋转 Treap 和 Splay 伸展树。所有模板代码对应题目 P3369 【模板】普通平衡树。
替罪羊树
替罪羊树使用一种简单粗暴的方法维持 BST 的平衡性:在插入/删除操作的时候,对于途经的节点,若发现某个子树不平衡,直接将其摧毁并重构出一棵平衡的子树。
重构不平衡子树的具体步骤如下:
- 中序遍历子树,得到权值序列(拍平)。实现时用一个栈维护节点的分配和回收。
- 以中间元素为根,仿照建立线段树的方式建树(拎起来)。
替罪羊树的基本操作(插入/删除/查找等),平摊时间复杂度为 O(\log n)。
最后需要解决的问题是对一棵子树是否平衡的判定,这里通过设定不平衡率 \alpha 解决:对于一棵子树,若它左子树或/右子树的大小占整棵树大小的比例超过 \alpha,就评定它不平衡,需要重构。
$\alpha$ 的选取直接影响到树的平衡性和重构次数,进而影响效率。在保证 BST 一定程度上的平衡同时要尽量减少重构次数。一般取 $\alpha=0.7$ 或 $0.75$ 的效率较高。
此外,删除操作时我们采用惰性删除,只对需要删除的节点打标记。过多的应删除节点也会降低效率,因此考虑未被删除的子树大小占比小于 $\alpha$ 的情况也重构子树。
概括替罪羊树的方法:设定适当的不平衡率 $\alpha$,依据这个判定标准暴力重构子树。
```cpp
#include<bits/stdc++.h>
using namespace std;
typedef double db;
const int N=1e5+5;
const db alpha=0.75;
static char buf[1000000],*p1=buf,*p2=buf;
#define getchar() p1==p2&&(p2=(p1=buf)+fread(buf,1,1000000,stdin),p1==p2)?EOF:*p1++
inline int wrd(){int x=0,f=1;char c=getchar();while(c<'0' || c>'9'){if(c=='-') f=-1;c=getchar();}while(c>='0' && c<='9') {x=(x<<3)+(x<<1)+c-48;c=getchar();}return x*f;}
inline void write(int x){static char buf[20];static int len=-1;if(x<0)putchar('-'),x=-x;do buf[++len]=x%10,x/=10;while(x);while(len>=0)putchar(buf[len--]+48);}
int n,m,rt,st[N],tp;
int od[N],len;
struct node{
int ls,rs,w,sz,tot;
bool rem; // 是否保留的标记,删除时置为 0
void init(){ls=rs=0,sz=tot=1,rem=1;}
}s[N];
#define ls(x) s[x].ls
#define rs(x) s[x].rs
#define w(x) s[x].w
#define sz(x) s[x].sz
#define tot(x) s[x].tot
#define rem(x) s[x].rem
bool isbad(int x){return alpha*sz(x)<=max(sz(ls(x)),sz(rs(x)));}
// maintain 只适用于 rebld,此时不存在应删的节点
void maintain(int x){sz(x)=sz(ls(x))+sz(rs(x))+1,tot(x)=tot(ls(x))+tot(rs(x))+1;}
void fla(int x){if(x) fla(ls(x)),(rem(x)?od[++len]:st[++tp])=x,fla(rs(x));}
int bld(int l,int r){
if(l>r) return 0;
int md=(l+r)>>1,x=od[md];
s[x].init();
ls(x)=bld(l,md-1),rs(x)=bld(md+1,r);
maintain(x); return x;
}
void rebld(int &x){len=0,fla(x),x=bld(1,len);}
void ins(int &x,int w){
if(!x){
x=st[tp--],s[x].init(),w(x)=w;
return;
}
++sz(x),++tot(x);
ins(w<=w(x)?ls(x):rs(x),w);
if(isbad(x)) rebld(x);
}
int rnk(int x,int w){ // +1 -> rank
if(!x) return 0;
return w<=w(x)?rnk(ls(x),w):sz(ls(x))+rem(x)+rnk(rs(x),w);
}
int kth(int x,int k){
if(!x) return -1;
if(rem(x) && sz(ls(x))+1==k) return w(x);
return k<=sz(ls(x))?kth(ls(x),k):kth(rs(x),k-sz(ls(x))-rem(x));
}
void del_kth(int x,int k){
if(!x) return;
--sz(x);
if(rem(x) && sz(ls(x))+1==k){rem(x)=0;return;}
k<=sz(ls(x))?del_kth(ls(x),k):del_kth(rs(x),k-sz(ls(x))-rem(x));
}
void del(int w){
del_kth(rt,rnk(rt,w)+1);
if(sz(rt)<=alpha*tot(rt)) rebld(rt);
}
int pre(int x){return kth(rt,rnk(rt,x));}
int nxt(int x){return kth(rt,rnk(rt,x+1)+1);}
signed main(){
n=1e5,m=wrd();
for(int i=1;i<=n;++i) st[++tp]=i;
while(m--){
int o=wrd(),x=wrd();
if(o==1) ins(rt,x);
else if(o==2) del(x);
else if(o==3) write(rnk(rt,x)+1),puts("");
else if(o==4) write(kth(rt,x)),puts("");
else if(o==5) write(pre(x)),puts("");
else if(o==6) write(nxt(x)),puts("");
}
return 0;
}
```
# 旋转 Treap
Treap 树的每个节点除了所有 BST 都有的键值 $w$ 外还拥有一个优先级 $priority$。Treap 同时满足 BST 的性质和堆的性质:
- (BST 性质)左子树的 $w$ 小于子树根节点的 $w$,右子树的 $w$ 大于根节点的 $w$。
- (大/小根堆性质)父节点的 $priority$ 大于/小于子节点的 $priority$。
Treap 的一个性质:若每个节点的键值和优先级已经确定且不同,建出的 BST 形态唯一。那么可以考虑通过赋予节点合适的优先级,并分别对 $w$ 和 $priority$ 维护 BST 和堆的性质,从而保证树的平衡。
实际上对于每个节点的 $priority$ 随机生成即可,可以认为是在维护堆性质时调整树的形态,效果相当于随机打乱了节点的插入顺序。这样期望的树高为 $O(\log n)$,也就保证了基本操作的时间复杂度正确。
最后解决采用什么手段维护 Treap 形态的问题,旋转 Treap 采用对节点的旋转实现各种操作。旋转分为左旋和右旋两种:
- 左旋(zag):把右儿子向左旋转成根节点。根节点成为原先右儿子的左儿子。原先右儿子的左儿子成为原先根节点现在的右儿子。
- 右旋(zig):与左旋对称,把左儿子向右旋转成跟你节点。根节点成为原先左儿子的右儿子,原先左儿子的右儿子成为原先根节点的左儿子。
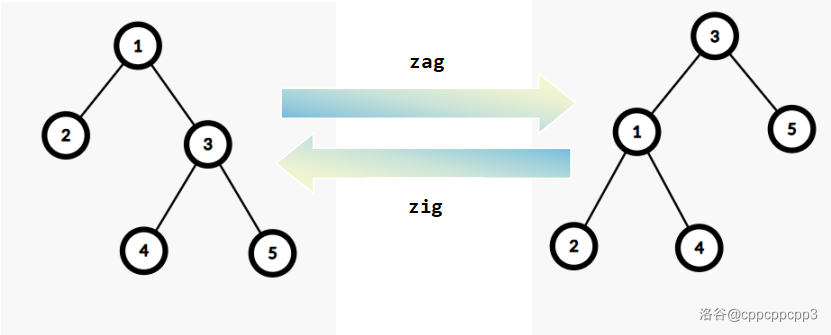
容易发现旋转操作仍然维持了 BST 的性质,且节点信息依然正确。
那么插入/删除时考虑是否把当前节点的左/右儿子旋转上来即可,查询操作与一般 BST 相同。
```cpp
#include<bits/stdc++.h>
using namespace std;
const int N=1e5+5;
static char buf[1000000],*p1=buf,*p2=buf;
#define getchar() p1==p2&&(p2=(p1=buf)+fread(buf,1,1000000,stdin),p1==p2)?EOF:*p1++
inline int wrd(){int x=0,f=1;char c=getchar();while(c<'0' || c>'9'){if(c=='-') f=-1;c=getchar();}while(c>='0' && c<='9') {x=(x<<3)+(x<<1)+c-48;c=getchar();}return x*f;}
inline void write(int x){static char buf[20];static int len=-1;if(x<0)putchar('-'),x=-x;do buf[++len]=x%10,x/=10;while(x);while(len>=0)putchar(buf[len--]+48);}
mt19937 rnd(time(0));
int m,rt,idx;
struct node{
int ls,rs,w,pr,sz,cnt;
void init(){ls=rs=0,sz=cnt=1,pr=rnd();}
}s[N];
#define ls(x) s[x].ls
#define rs(x) s[x].rs
#define w(x) s[x].w
#define pr(x) s[x].pr
#define sz(x) s[x].sz
#define cnt(x) s[x].cnt
void maintain(int x){sz(x)=sz(ls(x))+sz(rs(x))+cnt(x);}
// rotate(root,d) : ls/rs -> root
void rotate(int &x,bool d){
int k;
// d=0/1 -> left/right rotate
if(!d) k=rs(x),rs(x)=ls(k),ls(k)=x;
else k=ls(x),ls(x)=rs(k),rs(k)=x;
sz(k)=sz(x),maintain(x),x=k;
}
void ins(int &x,int w){
if(!x){
x=++idx,s[x].init(),w(x)=w;
return;
}
++sz(x);
if(w==w(x)) ++cnt(x);
else ins(w<w(x)?ls(x):rs(x),w);
if(ls(x) && pr(ls(x))>pr(x)) rotate(x,1);
if(rs(x) && pr(rs(x))>pr(x)) rotate(x,0);
}
void del(int &x,int w){
if(!x) return;
if(w==w(x)){
if(cnt(x)>1){--cnt(x),--sz(x);return;}
// 删除根节点,把 ls/rs 推上来
if(!ls(x) || !rs(x)) x=ls(x)|rs(x);
else if(ls(x) && pr(ls(x))>pr(rs(x))) rotate(x,1),del(rs(x),w);
else rotate(x,0),del(ls(x),w);
maintain(x); return;
}
del(w<w(x)?ls(x):rs(x),w),maintain(x);
}
int rnk(int x,int w){ // = rank
if(!x) return 1;
if(w==w(x)) return sz(ls(x))+1;
return w<w(x)?rnk(ls(x),w):rnk(rs(x),w)+sz(ls(x))+cnt(x);
}
int kth(int x,int k){
if(!x) return -1;
if(sz(ls(x))<k && k<=sz(ls(x))+cnt(x)) return w(x);
return k<=sz(ls(x))?kth(ls(x),k):kth(rs(x),k-sz(ls(x))-cnt(x));
}
int pre(int x){return kth(rt,rnk(rt,x)-1);}
int nxt(int x){return kth(rt,rnk(rt,x+1));}
signed main(){
m=wrd();
while(m--){
int o=wrd(),x=wrd();
if(o==1) ins(rt,x);
else if(o==2) del(rt,x);
else if(o==3) write(rnk(rt,x)),puts("");
else if(o==4) write(kth(rt,x)),puts("");
else if(o==5) write(pre(x)),puts("");
else if(o==6) write(nxt(x)),puts("");
}
return 0;
}
```
# Splay 树
Splay 树通过基于旋转的伸展(splay)操作维护平衡的 BST,其各种基本操作的时间复杂度也为均摊的 $O(\log n)$。
记整棵树的根节点为 $rt$,$x$ 的父节点为 $fa(x)$,下文记 $y=fa(x),z=fa(y)$。
**旋转(rotate)操作**:分为左旋 zag 和右旋 zig,与旋转 Treap 相同。下文中“对节点 $x$ 做旋转”指把 $x$ 旋转到父节点的位置。
**伸展(splay)操作**:借助旋转操作将节点 $x$ 提至根节点,每个步骤使 $x$ 上升一个位置。步骤有三类(六种)情况:
1. zig:当 $y=rt$ 时对 $x$ 进行左旋/右旋,使 $x$ 成为根节点。
2. zig-zig:$y\neq rt$ 且 $x,y$ 均为左/右儿子(即 $x,y,z$ 三点共线)时进行,先旋转 $y$ 再旋转 $x$。
3. zig-zag:$y\neq rt$ 且 $x,y$ 其一左其一右时执行,先旋转 $x$ 到 $y$,再旋转一次 $x$ 到 $z$ 处。
注意到 2/3 类步骤(双旋)每次可以将 BST 的层数减少 $1$,有效保证了树的平衡性。
Splay 树规定每次将访问到的节点通过伸展操作提至根处。
```cpp
#include<bits/stdc++.h>
using namespace std;
const int N=1e5+5;
static char buf[1000000],*p1=buf,*p2=buf;
#define getchar() p1==p2&&(p2=(p1=buf)+fread(buf,1,1000000,stdin),p1==p2)?EOF:*p1++
inline int wrd(){int x=0,f=1;char c=getchar();while(c<'0' || c>'9'){if(c=='-') f=-1;c=getchar();}while(c>='0' && c<='9') {x=(x<<3)+(x<<1)+c-48;c=getchar();}return x*f;}
inline void write(int x){static char buf[20];static int len=-1;if(x<0)putchar('-'),x=-x;do buf[++len]=x%10,x/=10;while(x);while(len>=0)putchar(buf[len--]+48);}
int n;
struct Splay{
int rt,idx,fa[N],ch[N][2],w[N],cnt[N],sz[N];
void maintain(int x){sz[x]=sz[ch[x][0]]+sz[ch[x][1]]+cnt[x];}
void clr(int x){fa[x]=ch[x][0]=ch[x][1]=w[x]=cnt[x]=sz[x]=0;}
bool get(int x){return x==ch[fa[x]][1];}
void rotate(int x){
int y=fa[x],z=fa[y],k=get(x);
ch[y][k]=ch[x][k^1];
if(ch[x][k^1]) fa[ch[x][k^1]]=y;
fa[y]=x,ch[x][k^1]=y;
fa[x]=z;
if(z) ch[z][y==ch[z][1]]=x;
maintain(y),maintain(x);
}
void splay(int x,int goal){ // 把 x 旋转成 goal 的儿子
if(!goal) rt=x;
while(fa[x]^goal){
int y=fa[x],z=fa[y];
if(z^goal) rotate(get(x)==get(y)?y:x);
rotate(x);
}
}
void ins(int k){
if(!rt){
rt=++idx,w[rt]=k,++cnt[rt];
maintain(rt); return;
}
int x=rt,y=0;
while(1){
if(w[x]==k){
++cnt[x],maintain(x);
splay(x,0); return;
}
y=x,x=ch[x][w[x]<k];
if(!x){
x=++idx,w[x]=k,++cnt[x],fa[x]=y,ch[y][w[y]<k]=x;
maintain(x),maintain(y);
splay(x,0); return;
}
}
}
int rnk(int k){
int as=0,u=rt;
while(1){
if(k<w[u]) u=ch[u][0];
else{
as+=sz[ch[u][0]];
if(!u) return as+1;
if(k==w[u]){splay(u,0);return as+1;}
as+=cnt[u],u=ch[u][1];
}
}
}
int kth(int k){
int u=rt;
while(1){
if(ch[u][0] && k<=sz[ch[u][0]]) u=ch[u][0];
else{
k-=(cnt[u]+sz[ch[u][0]]);
if(!u) return -1;
if(k<=0){splay(u,0);return w[u];}
u=ch[u][1];
}
}
}
int pre(){ // 先插入 x 并把 x 提至根,此时左儿子不断向右走就是前驱
int u=ch[rt][0];
if(!u) return u;
while(ch[u][1]) u=ch[u][1];
splay(u,0); return u;
}
int nxt(){ // 同理
int u=ch[rt][1];
if(!u) return u;
while(ch[u][0]) u=ch[u][0];
splay(u,0); return u;
}
void del(int k){
rnk(k);
if(cnt[rt]>1){
--cnt[rt],maintain(rt);
return;
}
if(!ch[rt][0]){
int u=rt; rt=ch[rt][1],fa[rt]=0;
clr(u); return;
}
if(!ch[rt][1]){
int u=rt; rt=ch[rt][0],fa[rt]=0;
clr(u); return;
}
int u=rt,x=pre();
fa[ch[u][1]]=x,ch[x][1]=ch[u][1];
clr(u); return;
}
}T;
signed main(){
n=wrd();
for(int i=1;i<=n;++i){
int o=wrd(),x=wrd();
if(o==1) T.ins(x);
else if(o==2) T.del(x);
else if(o==3) write(T.rnk(x)),puts("");
else if(o==4) write(T.kth(x)),puts("");
else if(o==5) T.ins(x),write(T.w[T.pre()]),puts(""),T.del(x);
else if(o==6) T.ins(x),write(T.w[T.nxt()]),puts(""),T.del(x);
}
return 0;
}
```
Splay 支持提根操作,因此可以提取区间,用来解决序列问题。
在维护序列的 Splay 上,位置 $i$ 对应的节点权值 $w$ 即为 $i$,通过查询第 $k$ 大可以 $O(\log n)$ 找到某一位置对应的节点。如果查找区间 $[l,r]$,把 $l-1$ 旋转到根,$r+1$ 旋转成 $l-1$ 的右儿子,此时 $r+1$ 的左子树就对应 $[l,r]$。
实现时预先插入位置 $0$ 和 $n+1$ 作为哨兵节点防止越界。注意不要忘记 splay 操作。
**区间翻转**
[P3391 【模板】文艺平衡树](https://www.luogu.com.cn/problem/P3391)
提取翻转区间的子树,需要按照子树的中序遍历顺序翻转。显然暴力递归交换左右儿子不可行,考虑引入线段树的 lazy tag。给根节点打上翻转懒标记并交换左右儿子,之后遍历到某个节点时下传标记。
```cpp
// Problem: P3391 【模板】文艺平衡树
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P3391
// Memory Limit: 125 MB
// Time Limit: 1000 ms
//
// Powered by CP Editor (https://cpeditor.org)
#include<bits/stdc++.h>
using namespace std;
const int N=1e5+5;
const int inf=1e9+7;
static char buf[1000000],*p1=buf,*p2=buf;
#define getchar() p1==p2&&(p2=(p1=buf)+fread(buf,1,1000000,stdin),p1==p2)?EOF:*p1++
inline int wrd(){int x=0,f=1;char c=getchar();while(c<'0' || c>'9'){if(c=='-') f=-1;c=getchar();}while(c>='0' && c<='9') {x=(x<<3)+(x<<1)+c-48;c=getchar();}return x*f;}
inline void write(int x){static char buf[20];static int len=-1;if(x<0)putchar('-'),x=-x;do buf[++len]=x%10,x/=10;while(x);while(len>=0)putchar(buf[len--]+48);}
int n,m,a[N];
struct Splay{
int rt,idx,fa[N],ch[N][2],sz[N],lz[N],w[N];
void maintain(int x){sz[x]=sz[ch[x][0]]+sz[ch[x][1]]+1;}
bool get(int x){return x==ch[fa[x]][1];}
void mdf(int x){swap(ch[x][0],ch[x][1]),lz[x]^=1;}
void pd(int x){if(lz[x]) mdf(ch[x][0]),mdf(ch[x][1]),lz[x]=0;}
void rotate(int x){
int y=fa[x],z=fa[y],k=get(x);
pd(y),pd(x);
ch[y][k]=ch[x][k^1];
if(ch[x][k^1]) fa[ch[x][k^1]]=y;
fa[y]=x,ch[x][k^1]=y;
fa[x]=z;
if(z) ch[z][y==ch[z][1]]=x;
maintain(y),maintain(x);
}
void splay(int x,int goal){
if(!goal) rt=x;
while(fa[x]^goal){
int y=fa[x],z=fa[y];
if(z^goal) rotate(get(x)==get(y)?y:x);
rotate(x);
}
}
int bld(int l,int r,int f){
if(l>r) return 0;
int md=(l+r)>>1,u=++idx;
w[u]=a[md],fa[u]=f;
ch[u][0]=bld(l,md-1,u),ch[u][1]=bld(md+1,r,u);
maintain(u); return u;
}
int kth(int k){
int u=rt;
while(1){
pd(u);
if(ch[u][0] && k<=sz[ch[u][0]]) u=ch[u][0];
else{
k-=(sz[ch[u][0]]+1);
if(k<=0){splay(u,0);return u;}
u=ch[u][1];
}
}
}
void reverse(int l,int r){
int L=kth(l),R=kth(r+2); // [0,n+1]: l(-th)=l-1,(r+2)(-th)=r+1
splay(L,0),splay(R,L),mdf(ch[R][0]);
}
void dfs(int x){
pd(x);
if(ch[x][0]) dfs(ch[x][0]);
if(w[x] && w[x]<=n) write(w[x]),putchar(' ');
if(ch[x][1]) dfs(ch[x][1]);
}
}T;
signed main(){
n=wrd(),m=wrd();
for(int i=0;i<=n+1;++i) a[i]=i;
T.rt=T.bld(0,n+1,0);
while(m--){
int l=wrd(),r=wrd();
T.reverse(l,r);
}
T.dfs(T.rt);
return 0;
}
```
**区间修改**
如区间加减,沿用 lazy tag 即可。
**区间插入/删除**
设在位置 $pos$ 后插入,提取 $pos$ 对应节点为根节点,$pos+1$ 对应节点为其右儿子,以 $pos+1$ 对应节点的左儿子为根仿照线段树递归建一棵平衡的树。
删除区间 $[l,r]$,提取出子树并清除根节点的信息。
[Problem](https://www.luogu.com.cn/problem/P4008)
Splay 维护序列的模板题,代码如下:
```cpp
#include<bits/stdc++.h>
using namespace std;
const int N=3e6+5;
int m,loc;
char op[10],A[N];
struct Splay{
int rt,idx,fa[N],ch[N][2],sz[N];
char w[N];
void maintain(int x){sz[x]=sz[ch[x][0]]+sz[ch[x][1]]+1;}
void clr(int x){fa[x]=ch[x][0]=ch[x][1]=sz[x]=w[x]=0;}
bool get(int x){return x==ch[fa[x]][1];}
int addnew(char v,int f){
int x=++idx;
fa[x]=f,w[x]=v,sz[x]=1;
return x;
}
void init(){
rt=loc=1,idx=2;
sz[1]=2,ch[1][1]=2,w[1]='\n';
sz[2]=1,fa[2]=1,w[2]='\n';
}
void rotate(int x){
int y=fa[x],z=fa[y],k=get(x);
ch[y][k]=ch[x][k^1];
if(ch[x][k^1]) fa[ch[x][k^1]]=y;
fa[y]=x,ch[x][k^1]=y;
fa[x]=z;
if(z) ch[z][y==ch[z][1]]=x;
maintain(y),maintain(x);
}
void splay(int x,int goal){
if(!goal) rt=x;
while(fa[x]^goal){
int y=fa[x],z=fa[y];
if(z^goal) rotate(get(x)==get(y)?y:x);
rotate(x);
}
}
int bld(int l,int r,int f,char *A){
int md=(l+r)>>1,x=addnew(A[md],f);
if(l<md) ch[x][0]=bld(l,md-1,x,A);
if(md<r) ch[x][1]=bld(md+1,r,x,A);
maintain(x); return x;
}
int kth(int k){
int u=rt;
while(1){
if(ch[u][0] && k<=sz[ch[u][0]]) u=ch[u][0];
else{
k-=(sz[ch[u][0]]+1);
if(k<=0){splay(u,0);return u;}
u=ch[u][1];
}
}
}
void ins(int len,char *A){
int l=kth(loc),r=kth(loc+1);
splay(l,0),splay(r,l);
ch[ch[rt][1]][0]=bld(0,len-1,ch[rt][1],A);
maintain(ch[rt][1]),maintain(rt);
}
void del(int len){ // delete [loc+1,loc+len]
int l=kth(loc),r=kth(loc+len+1);
splay(l,0),splay(r,l);
clr(ch[ch[rt][1]][0]);
maintain(ch[rt][1]),maintain(rt);
}
void dfs(int u){
if(ch[u][0]) dfs(ch[u][0]);
if(w[u]>=32&&w[u]<=126) putchar(w[u]);
if(ch[u][1]) dfs(ch[u][1]);
}
void write(int len){
int l=kth(loc),r=kth(loc+len+1);
splay(l,0),splay(r,l);
dfs(ch[ch[rt][1]][0]);
}
}T;
signed main(){
scanf("%d",&m),T.init();
while(m--){
int len;
scanf("%s",op);
if(op[0]=='M'){
scanf("%d",&loc),++loc; // 开头插入了哨兵
}else if(op[0]=='P'){
--loc;
}else if(op[0]=='N'){
++loc;
}else if(op[0]=='I'){
scanf("%d",&len),strcpy(A,"");
for(int i=0,fl=0;i<len;++i){
char c=getchar();
fl|=(c>=32&&c<=126);
if(!fl||c<32||c>126) --i;
else A[i]=c;
}
T.ins(len,A);
}else if(op[0]=='D'){
scanf("%d",&len);
T.del(len);
}else if(op[0]=='G'){
scanf("%d",&len);
T.write(len),puts("");
}
}
return 0;
}
```
# 树套树
[P3380 【模板】树套树](https://www.luogu.com.cn/problem/P3380)
本题需要区间查询,考虑线段树套平衡树,每个节点维护一棵平衡树(动态开点)。外层将区间划分成 $O(\log n)$ 段,内层处理每段区间的基本操作。
- 单点修改:对所有线段树上包含该位置的节点,在平衡树上删除、加入,$O(\log^2n)$。
- 查询前驱/后继:在每段区间上查前驱/后继,全部取 max/min,$O(\log^2n)$。
- 根据值查排名:在每段区间上查比它小的数的个数,加和再加 $1$ 即为排名,$O(\log^2n)$。
- 根据排名查值:二分答案,再根据二分的值查到的排名来调整这个值。$O(\log^3n)$。
时间复杂度劣于树状数组套主席树的 $O(\log^2 n)$。树套树的空间复杂度巨大,可以考虑其它的替代方案如块状链表或离线算法。
```cpp
// Problem: P3380 【模板】树套树
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P3380
// Memory Limit: 512 MB
// Time Limit: 2000 ms
//
// Powered by CP Editor (https://cpeditor.org)
#include<bits/stdc++.h>
using namespace std;
const int N=5e4+5;
const int inf=INT_MAX;
static char buf[1000000],*p1=buf,*p2=buf;
#define getchar() p1==p2&&(p2=(p1=buf)+fread(buf,1,1000000,stdin),p1==p2)?EOF:*p1++
inline int wrd(){int x=0,f=1;char c=getchar();while(c<'0' || c>'9'){if(c=='-') f=-1;c=getchar();}while(c>='0' && c<='9') {x=(x<<3)+(x<<1)+c-48;c=getchar();}return x*f;}
inline void write(int x){static char buf[20];static int len=-1;if(x<0)putchar('-'),x=-x;do buf[++len]=x%10,x/=10;while(x);while(len>=0)putchar(buf[len--]+48);}
int n,m,a[N],MX,MN=inf;
struct seg_splay{
int idx,rt[N<<2],fa[N*50],w[N*50],ch[N*50][2],cnt[N*50],sz[N*50];
void maintain(int x){sz[x]=sz[ch[x][0]]+sz[ch[x][1]]+cnt[x];}
bool get(int x){return x==ch[fa[x]][1];}
void clr(int x){fa[x]=w[x]=ch[x][0]=ch[x][1]=cnt[x]=sz[x]=0;}
void rotate(int x){
int y=fa[x],z=fa[y],k=get(x);
ch[y][k]=ch[x][k^1];
if(ch[x][k^1]) fa[ch[x][k^1]]=y;
fa[y]=x,ch[x][k^1]=y;
fa[x]=z;
if(z) ch[z][y==ch[z][1]]=x;
maintain(y),maintain(x);
}
void splay(int o,int x,int goal){
if(!goal) rt[o]=x;
while(fa[x]^goal){
int y=fa[x],z=fa[y];
if(z^goal) rotate(get(x)==get(y)?y:x);
rotate(x);
}
}
void ins(int o,int k){
if(!rt[o]){
rt[o]=++idx,w[rt[o]]=k,++cnt[rt[o]];
maintain(rt[o]); return;
}
int x=rt[o],y=0;
while(1){
if(k==w[x]){
++cnt[x],maintain(x),maintain(y);
splay(o,x,0); return;
}
y=x,x=ch[x][w[x]<k];
if(!x){
x=++idx,w[x]=k,++cnt[x];
fa[x]=y,ch[y][w[y]<k]=x;
maintain(x),maintain(y);
splay(o,x,0); return;
}
}
}
int rnk(int o,int k){
int u=rt[o],as=0;
while(1){
if(k<w[u]) u=ch[u][0];
else{
as+=sz[ch[u][0]];
if(!u) return as+1;
if(k==w[u]){splay(o,u,0);return as+1;}
as+=cnt[u],u=ch[u][1];
}
}
}
int kth(int o,int k){
int u=rt[o];
while(1){
if(ch[u][0] && k<=sz[ch[u][0]]) u=ch[u][0];
else{
k-=(cnt[u]+sz[ch[u][0]]);
if(k<=0){splay(o,u,0);return w[u];}
u=ch[u][1];
}
}
}
int pre(int o){
int u=ch[rt[o]][0];
if(!u) return u;
while(ch[u][1]) u=ch[u][1];
splay(o,u,0); return u;
}
int nxt(int o){
int u=ch[rt[o]][1];
if(!u) return u;
while(ch[u][0]) u=ch[u][0];
splay(o,u,0); return u;
}
void del(int o,int k){
rnk(o,k);
if(cnt[rt[o]]>1){
--cnt[rt[o]];
maintain(rt[o]); return;
}
if(!ch[rt[o]][0] && !ch[rt[o]][1]){
clr(rt[o]),rt[o]=0; return;
}
if(!ch[rt[o]][0]){
int u=rt[o];
rt[o]=ch[rt[o]][1],fa[rt[o]]=0;
clr(u); return;
}
if(!ch[rt[o]][1]){
int u=rt[o];
rt[o]=ch[rt[o]][0],fa[rt[o]]=0;
clr(u); return;
}
int u=rt[o],x=pre(o);
fa[ch[u][1]]=x,ch[x][1]=ch[u][1];
clr(u),maintain(x);
}
#define ls (t<<1)
#define rs (t<<1|1)
#define md ((l+r)>>1)
void add(int l,int r,int t,int x,int k){
ins(t,k);
if(l==r) return;
x<=md?add(l,md,ls,x,k):add(md+1,r,rs,x,k);
}
void upd(int l,int r,int t,int x,int k){
del(t,a[x]),ins(t,k);
if(l==r) return;
x<=md?upd(l,md,ls,x,k):upd(md+1,r,rs,x,k);
}
int gt(int l,int r,int t,int x,int y,int k){ // +1 -> rank
if(l>y || r<x) return 0;
if(l>=x&&r<=y) return rnk(t,k)-1;
return gt(l,md,ls,x,y,k)+gt(md+1,r,rs,x,y,k);
}
int pre(int l,int r,int t,int x,int y,int k){
if(l>y || r<x) return -inf;
if(l>=x&&r<=y){
ins(t,k); int as=pre(t); del(t,k);
return !as?-inf:w[as];
}
return max(pre(l,md,ls,x,y,k),pre(md+1,r,rs,x,y,k));
}
int nxt(int l,int r,int t,int x,int y,int k){
if(l>y || r<x) return inf;
if(l>=x&&r<=y){
ins(t,k); int as=nxt(t); del(t,k);
return !as?inf:w[as];
}
return min(nxt(l,md,ls,x,y,k),nxt(md+1,r,rs,x,y,k));
}
int Kth(int ql,int qr,int k){
int l=MN,r=MX,as=MN;
while(l<=r){
int mid=(l+r)>>1;
if(gt(1,n,1,ql,qr,mid)+1<=k) as=mid,l=mid+1;
else r=mid-1;
}
return as;
}
}T;
signed main(){
n=wrd(),m=wrd();
for(int i=1;i<=n;++i){
a[i]=wrd(),T.add(1,n,1,i,a[i]);
MX=max(MX,a[i]),MN=min(MN,a[i]);
}
while(m--){
int o=wrd(),l=wrd(),r=wrd(),k;
if(o==3){
T.upd(1,n,1,l,r),a[l]=r;
MX=max(MX,r),MN=min(MN,r);
continue;
}
k=wrd();
if(o==1) write(T.gt(1,n,1,l,r,k)+1),puts("");
else if(o==4) write(T.pre(1,n,1,l,r,k)),puts("");
else if(o==5) write(T.nxt(1,n,1,l,r,k)),puts("");
else write(T.Kth(l,r,k)),puts("");
}
return 0;
}
```