斜率/四边形不等式优化 笔记

# 斜率优化DP ## 前置姿势 ### 1. 单调队列，DP，以及单调队列优化DP 单调队列用来维护一个滑动区间的最大值，因为最多滑动不超过2n次，复杂度O(n). [P1886 滑动窗口](https://www.luogu.org/problem/P1886)是单调队列的模板题。 在线性DP很常用 [P3957 跳房子](https://www.luogu.org/problem/P3957) 就是一道经典的单调队列优化动归... （当时在考场上遇到这道题毫无头绪，现在却变成了简单题....想起来感慨很深啊... 设$f_i$为到第$i$的花费，依次遍历$i$ 因为每个点是由一个区间转移过来的，而这个区间随着i的右移也右移，所以满足单调队列优化的条件，优化后可达到$O(n)$ [P3572 [POI2014]PTA-Little Bird](https://www.luogu.org/problem/P3572) 与上道题基本一样... ### 2.一次函数 初中基本知识不谈 ## 正文 这里有一个经典的问题 有一个长度为n的正整数序列，要求划分成若干段，每一段的代价为这段的和的平方+m，求划分序列的最小代价 考虑m=0，显然划分越多次越好，直接划成n段 但是有了m，划分多一段，代价就会多m，划分成n段是不划算的 先考虑$O(n^2)$的DP做法 设$s_i$为原序列前缀和，$f_i$ 为划分前k个数最小代价，显然有 $f_i=min\{f(k)+(s_i-s_k)^2\}+m$ 对于每一个$i$，枚举断点$k$即可，时间复杂度$O(n^2)$ 斜率优化要对上面这个式子进行优化 首先复读一遍式子 $f_i=min\{f(k)+(s_i-s_k)^2\}+m$ 用完全平方公式展开 $f_i=min\{f(k)+s_i^2-2s_is_k+s^2_k\}+m$ 发现$k$怎么取值，$s_i^2$都一定不变 $f_i=min\{f(k)-2s_is_k+s^2_k\}+m+s_i^2$ 移项，得 $f_k+s_k^2=2s_i^2s_k^2+f_i+s_i^2-m$（取一个k，使得$f_i$最小） 将上面的式子转为一次函数 令$Y_k=f_k+s_k^2,X_k=s_k,B=f_i+s_i^2-m$ 有$Y_k=2s_iX_k+B$ 那么$B=f_i+s_i^2-m$即为一条过$(X_k,Y_k)$，斜率为$2s_i$的直线，在y轴上的截距，因为$s_i^2$ 和$m$都是常量，所以当$f_i$最小，$B$即最小 那么对于每个点i，前面就有$i-1$个断点，我们要在这$i-1$个点钟找到一个点，使得截距最小（也就是$f_i$最小） 再公式化地表述 就是有一条过$(s_k,f(k)+s^2_k)$，斜率为$2s_i$的直线，截距为$f(i)-s_i^2-m$，找一个点$k$使得截距最小 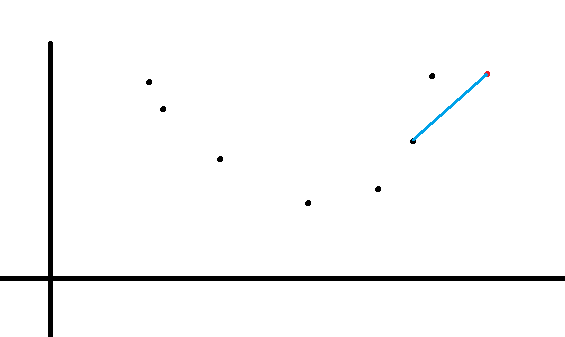如果有三个点$A,B,C(x_A<x_B<x_C),x$表示横坐标，且$B$在直线$AC$的上方，那么B肯定不是最优决策  红色线为最优决策，蓝色线为选B时的决策 发现选B永远不如选A或C好（截距较大、注意截距可以为负数） 那么所有的有可能对答案有贡献的点，会形成一个下凸壳 （下凸壳就是对于任意三点$i,j,k$(按横坐标排序)，$j$不在$i$与$k$的连线上方） 类比于单调队列，我们每次加入一个可能可以转移的状态，就可以删掉一些无用的状态 我们发现，我们每次的$X_k=s_k$，即横坐标，是单调上升的（因为$s_k$是正整数序列的前缀和），所以我们加入的决策点一个比一个偏右 这就类似于单调队列，下面模拟一下删点的过程 这是我们原来的图，红色为新加的点  连线，发现我们倒数第二个点不满足下凸壳，删去  继续连线  发现下一个点也不满足下凸壳，删去   最后连一次线，发现满足  最后的形状  另外，我们可以证明，若第$i$个点满足下凸壳，则$1,2,3,\dots,i-1$这些点全部满足下凸壳。 我们发现这个过程和单调队列几乎完 全 一 致，类似于单调队列，这个过程也可以用deque来维护，每个点至多进队一次，出队一次，这样扫过去的复杂度是$O(n)$的 以上就是加点的过程，接下来我们来看如何找到最小截距 我们发现，在这道题中我们加入的点的横坐标和直线的斜率都是递增的 再重新看一下我们的任务吧... 有一条过$(s_k,f(k)+s^2_k)$，斜率为$2s_i$的直线，截距为$f(i)-s_i^2-m$，找一个点$k$使得截距最小 接下来我们要找一个点使得截距最小 我们的方法是把队首弹出直至队首两个点的斜率大于等于$2s_i$，此时队首就是最优决策点 按上面的步骤做即可 ### P2900 [[UASACO08MAR]土地征用Land Acquisition](https://www.luogu.org/problem/P2900) 给n个长方形 有长和宽，每次选一组土地一起购买，代价为最长的长乘上最长的宽 求最小代价 显然如果存在$x_j\leq x_i,y_j<y_i$，那么这个$j$对答案没有贡献 那么我们把长方形按长从小到大排序，可以发现每次购买的肯定是连续一段 （如果不连续肯定不是最优） 还是考虑最原始的DP，设$f_i$为买前i块的最小代价，那么有 $f_i=min\{f_j+w_ih_{j+1}\}$ 仍然移项 $f_j=-w_ih_{j+1}+f_i$，答案为一个$j$使得$f_i$（也就是截距）最小 类似于上一道例题，点是$(-h_{j+1},f_i)$，斜率是$w_i$ 用上面的方法做即可 ```cpp #include<bits/stdc++.h> using namespace std; const int INF=(1<<30); const int maxn=100010; typedef long long ll; typedef double db; inline int read() { int res=0,fh=1; char ch=getchar(); while((ch>'9'||ch<'0')&&ch!='-')ch=getchar(); if(ch=='-')fh=-1,ch=getchar(); while(ch>='0'&&ch<='9')res=res*10+ch-'0',ch=getchar(); return fh*res; } int n,q[maxn],head,tail; ll f[maxn]; db k[maxn]; struct node{ ll h,w; }sq[maxn]; inline bool cmp(node a,node b){return a.h==b.h?a.w>b.w:a.h>b.h;} inline db work(int x,int y){return (f[x-1]-f[y-1])/(sq[y].h-sq[x].h);} int main() { n=read(); for(int i=1;i<=n;i++) sq[i]=(node){read(),read()}; sort(sq+1,sq+1+n,cmp); int cnt=1; for(int i=1;i<=n;i++) if(sq[cnt].w<sq[i].w)sq[++cnt]=sq[i]; n=cnt,head=1,tail=0; for(int i=1;i<=n;i++){ while(head<tail&&k[tail-1]>=work(i,q[tail]))tail--; k[tail]=work(i,q[tail]);q[++tail]=i; while(head<tail&&k[head]<sq[i].w)++head; f[i]=f[q[head]-1]+sq[q[head]].h*sq[i].w; } return printf("%lld\n",f[n]),0; } ``` ## 总结 我们发现我们的斜率dp式子，都是知道斜率和点值，使得截距最小 我们对暴力的DP式子移项，让我们要取的最小量（或者最大量）成为截距，决策点为下凸壳，可以由单调队列维护，也要使得斜率固定，这样的式子就可以用斜率优化+单调队列优化。 大概就是满足$f_i=min/max\{f_j+w(i,j)\}$的式子 # 四边形不等式优化 update on 19/08/16 因为我在写下这行东西的时候还不会四边形不等式优化，所以这篇文章也是学习笔记2333 [P4767 [IOI2000]邮局](https://www.luogu.org/problemnew/solution/P4767) ~~听说这题可以wqs二分...~~ 给定一个数轴，数轴上有n个关键点，要设立p个邮局，使得关键点到最近邮局的距离之和最小 如果p=1，那么根据常识，建在中间最好 其他的情况，设$f_{i,j}$为前i个关键点，设立j个邮局的最小花费 显然有 $$f_{i,j}=min\{f_{i,j},f_{k,j-1}+dis(k+1,i)\}$$ $dis_{l,r}$ 表示我们在l和r之间设立邮局后对答案产生的贡献 根据常识，放在中间最小 考虑如何$O(1)$计算$dis_{l,r}$ 先记录$s_{l,r}$为$l$到$r$坐标前缀和 ```cpp for(int i = 1; i <= n; i++) for (int j = i; j <= n; j++) s[i][j] = s[i][j - 1] + a[j]; ``` 则有 ``` dis[l][r] += (mid - l) * a[mid] - s[l][mid - 1]; dis[l][r] += s[mid + 1][r] - (r - mid) * a[mid]; ``` 对于每个$i$，枚断点$k$和$j$得到答案，时间复杂度$O(n^2m)$ 接下来是四边形不等式的结论 若决策单调，且满足 $$f_{a,c}+f_{b,d} \leq f_{a,d}+f_{b,c}(a\leq b\leq c\leq d)$$ 则$f_{i,j}$可以只由$f_{i,j-1},f{i+1,j}$中的一个状态的最优决策点（共四个）转移得。（这个点我刚刚理解错了...需要看代码...） 不知道听哪个老哥说网上的所有证明都是假的...但是我还是随便抄一个证明感性理解一下吧 其中决策单调指对于每个$i$，考虑到的最优决策点为$j$，那么$i+1$的最优决策点大于等于$j$ 这个在这题显然成立，对于$f_{a,c}+f_{b,d} \leq f_{a,d}+f_{b,c}$，在考场上一般通过打表得出...