三角函数入门
_LHF_
·
·
个人记录
三角函数
如果大家不知道三角函数的话可以看一看这里。
第一阶段
正弦函数
用\sin来表示正弦函数,是sine的缩写,先说说狭义的三角函数
根据相似三角形可以知道,在直角三角形内,若一个锐角是定值,那么它的对边和斜边的比是一个定值。
如果你连相似都不会的话……
例如,在一个等腰直角三角形中,两个锐角都是45°,如图:
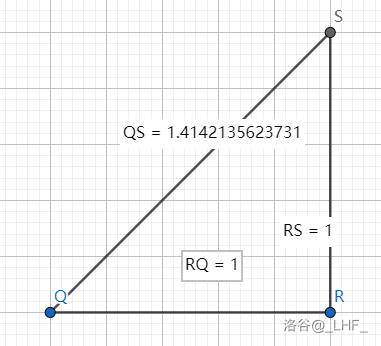
那么可以得出,$\displaystyle\sin 45^\circ=\frac{1}{\sqrt 2}=\frac{\sqrt 2}{2}
再举个栗子。
小奥学过,含30°的直角三角形对边是斜边的一半,那么\displaystyle\sin30^\circ=\frac{1}{2}
余弦函数
用cos来表示余弦函数。
注意,cos其实是cosine的缩写,但仍念作cosine
同样的,\cos x^\circ表示在一个直角三角形内一个度数为x的锐角的邻边和斜边的比值。
例如,由等腰三角形的性质可得,\displaystyle\cos 45^\circ=\frac{\sqrt 2}{2}
再比如,\displaystyle\cos 60^\circ=\frac{1}{2},\cos 30^\circ=\frac{\sqrt3}{2}
结合一下
我们会发现一条十分有趣的性质:\sin^2α+\cos^2α=1
正切函数
正切函数英文为tangent(简写\tan,旧为tg)
现在的教材通常都用\tan来表示
例如,$\tan 45^\circ=1,\tan30^\circ=\frac{\sqrt3}{3},\tan60^\circ=\sqrt3
结合一下
我们又会发现一条十分有趣的性质:\displaystyle\frac{\sin\alpha}{\cos\alpha}=\tan\alpha
余切函数
用cot表示余切函数
全称是cotangent。
例如,$\displaystyle\cot 45^\circ=1,\cot60^\circ=\frac{\sqrt3}{3},\cot30^\circ=\sqrt3
再结合一下
我们又会发现一条有趣的性质:\displaystyle\tan α=\frac{1}{\cot α}
正(余)割函数
用sec来表示正割函数,其全程为secant
用csc来表示余割函数,其全程为cosecant
例如,$\sec 45^\circ=\sqrt2 ,\csc60^\circ=2
当然,这两种函数并不在初中的教材上,也不再高中的教材上,但高等数学书上有。
总结一下
我们可以得到以下几条结论
\sin^2α+\cos^2α=1
\tan α=\frac{1}{\cot α}
\sec α=\frac{1}{\sin α}
\csc α=\frac{1}{\cos α}
第二阶段
先来说一说任意角的概念以及弧度制吧
在我们初中数学中,我们只见过锐角、直角、钝角、平角、周角。
在这里,我们要学习任意角。
例如181^\circ,-32^\circ这样的角。
比如像这幅图:
然后是弧度制。
聪明的小朋友可能会发现,我在写\sin 30^\circ=\frac{1}{2}这类式子的时候加了个^\circ,但是在写结论的时候没有加,这是为什么呢?看完就知道了。
其实角度还有一种表示方式,叫做弧度制,也就是那个角度对应的一个半径为1的扇形的弧长,比如这幅图,阴影部分的扇形弧长就是这里的弧度。
弧度前面通常不加字母。在计算机上,你可以看到RAD,这就表示使用弧度制。
如\displaystyle180^\circ=\pi,90^\circ=\frac{\pi}{2},60^\circ=\frac{\pi}{3},360^\circ=2\pi,-270^\circ=-\frac{3\pi}{2}
然后就是运用到三角函数中。
\displaystyle\sin\frac{\pi}{4}=\frac{\sqrt2}{2}
这时就发现了,三角函数在之前必须是锐角才行啊。
于是数学家便补了一个坑。
如图,在坐标原点画一个单位圆(即边长为1的圆),如图。
设∠CAB=a,C(x,y)
那么\sin a=y,\cos a=x
所以当a\in(\pi,2\pi),\sin a为负数
当a=k\pi,k\in Z时,\sin a=0
再比如当a为锐角的时候\cos a为正,当a为钝角的时候\cos a为负,当a为直角时\cos a=0。
这样子还可以得到:\tan a=\frac{y}{x}
所以\tan\frac{\pi}{2}不存在。
顺便给一下三角函数的图像以及性质:
这里引用一张比较好的图来说明正余弦函数的构造(如果看不到多刷新几次就可以了)
和差角公式
\sin(α\pmβ)=\sinα\cosβ\pm\cosα\sinβ
\cos(α\pmβ)=\cosα\cosβ\mp \sinα\sinβ
这是基本的和差角公式。
推导过程:略。
有兴趣的可以自己去了解一下。
利用这些东西,可以研究出许多新东西:
第三阶段
刚才一直在讲三角函数在代数中的运用,现在讲一下在几何中的应用。
首先,先画出一个美丽的三角形,如图。
面积
\displaystyle S_{\triangle ABC}=\frac{1}{2}ab\sin C=\frac{1}{2}ac\sin B=\frac{1}{2}bc\sin A
很简单,可以直接用作高+死套定义得出。
正弦定理:
### 余弦定理:
$c^2=a^2+b^2-2ab\cos C
顺便补充一个跟垂心有关的定理
如图,在非直角{\triangle ABC}中,G为垂心。
那么:\frac{AG}{|\cos A|}=\frac{BG}{|\cos B|}=\frac{CG}{|\cos C|}=2R
杂题
例一:
求函数y=\sin x+\cos x的值域。
注意了!这里十分关键。
我们知道:
所以\displaystyle\cos(x-\frac{\pi}{2})=\frac{\sqrt2}{2}\sin x+\frac{\sqrt2}{2}\cos x
嗯嗯,那么\displaystyle\sqrt 2\cos(x-\frac{\pi}{2})=\sin x+\cos x
所以:该函数的值域是[-\sqrt2,\sqrt2]
例二:
求证:tan^2a+1=\sec^2a(a≠\frac{(2k+1)\pi}{2},k\in Z)
用普通的方法做,的确挺麻烦的,但我们可以从基本定义出发。
可以得到:\displaystyle\tan^2a=\frac{y^2}{x^2}
所以\displaystyle\tan^2a+1=\frac{x^2+y^2}{x^2}
因为是在一个单位圆的边上,由勾股定理得:x^2+y^2=1
所以tan^2a+1=\frac{1}{x^2}=\sec^2x
例三:
求\displaystyle\frac{2\cos^25^\circ-1}{\sin40^\circ\cos40^\circ}
先补充点东西:
\cos2a=2\cos^2a-1,\sin2a=2\sin a\cos a
那么原式\displaystyle=\frac{cos 10^\circ}{\frac{1}{2}\sin80^\circ}=\frac{2\cos10^\circ}{\cos10^\circ}=2
例四:
尺规作图:做一个正五边形
看到题目的第一眼:这跟三角函数有什么关系
但我告诉你:这真的有关
先引入一个东西:\cos 3x=4\cos^3x-3\cos x,这东西可以用和差角公式证明。
然后开始:
如果我们能够构造出一个角,度数为108^\circ的因数的话,那就好办多了。
然后我们发现:\cos 54^\circ=\sin36^\circ
然后我们又发现:54=3\times18,36=2\times18
所以得到了:
4\cos^318^\circ-3\cos18^\circ=2\sin18^\circ\cos18^\circ
同时消掉一个\cos18^\circ得到:
4\cos^218^\circ-3=2\sin18^\circ
然后得到
4(1-sin^218^\circ)-3=2\sin18^\circ
\sin18^\circ=\frac{\sqrt5-1}{4}
然后因为
\cos2a=2\cos^2a-1
变形一下得:
\cos2a=1-2\sin^2a
得到:\displaystyle\cos36^\circ=\frac{1+\sqrt5}{4}
给出一种做法(仅供参考)
例五
来一道几何题
如图,在平行四边形ABCD中,作AE\perp CD,AF\perp BD,H是{\triangle AEF}的垂心,求证:AH^2+EF^2=AD^2
这一题可以用三角函数秒杀掉。
首先可以得到:A,E,F,D四点共圆,并且AD是{\triangle AEF}外接圆半径的两倍。所以\frac{AH}{|\cos∠EAF|}=CD,\frac{EF}{\sin∠EAF}=CD,因为这里∠EAF是锐角,所以可以去掉绝对值,得到AH=CD\times\cos∠EAF,EF=CD\times\sin∠EAF,所以AH^2+EF^2=AD^2。
例六
来一道跟信息学有关的。
区间加区间sin和
其实并不难,我们知道
\sin(α\pmβ)=\sinα\cosβ\pm\cosα\sinβ
\cos(α\pmβ)=\cosα\cosβ\mp \sinα\sinβ
然后……做完了。
线段树简单的维护一下就可以了。
总结一下
三角函数是一个很好的东西,在许多方面它都发挥着巨大的作用。
所以作者希望大家能够学好三角函数。
彩蛋
下面给出几个东西的证明
1.正弦定理
我们知道,\displaystyle S_{\triangle ABC}=\frac{1}{2}ab\sin C=\frac{1}{2}ac\sin B=\frac{1}{2}bc\sin A,然后同时除以\displaystyle\frac{abc}{2}即可。
但如何证明\displaystyle\frac{a}{\sin A}=2R呢?
如图,
设BD是\triangle ABC的外接圆半径,连接CD。
得到∠CDB=∠CAB
又因为BD\times\sin∠CDB=CB=a
所以\displaystyle BD=\frac{a}{\sin∠BCD}=\frac{a}{\sin A}
补充一个东西:向量,请认真看完链接之后继续往下看。
2.余弦定理
如图,在\triangle ABC中,有\vec{a}-\vec{b}=\vec c
两边同时平方,得\vec c^2=(\vec a-\vec b)^2
然后根据向量乘法法则,得到c^2=a^2+b^2-2ab\cos C
3.和(差)角公式
如图,作一个单位圆,设∠BOC=\alpha,∠BOD=\beta
所以C(\cos\alpha,\sin\alpha),D(\cos\beta,\sin\beta)
然后得到\vec{OC}·\vec{OD}=\cos(\alpha-b)=\cosα\cosβ+ \sinα\sinβ
然后就根据这个公式推导出其他公式了。
完美撒花
update 2021.4.14 感谢 @zhy137036 指出了一处错误