解二维不可压缩流体的 NS 方程
cancan123456
·
·
个人记录
首先我们略过一堆一堆的推导,直接上方程:
\begin{cases}\nabla\cdot\vec u=0\\\frac{\partial\vec u}{\partial t}+\vec u\cdot\nabla\vec u=-\frac1\rho\nabla p+\nu\nabla^2\vec u\end{cases}
我们展开写一下:
$$\begin{cases}\frac{\partial u}{\partial t}+u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}=-\frac1\rho\frac{\partial p}{\partial x}+\nu\frac{\partial^2u}{\partial x^2}+\nu\frac{\partial^2u}{\partial y^2}\\\frac{\partial v}{\partial t}+u\frac{\partial v}{\partial x}+v\frac{\partial v}{\partial y}=-\frac1\rho\frac{\partial p}{\partial y}+\nu\frac{\partial^2v}{\partial x^2}+\nu\frac{\partial^2v}{\partial y^2}\\\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}=0\end{cases}$$
我们采取这样的交错网格:
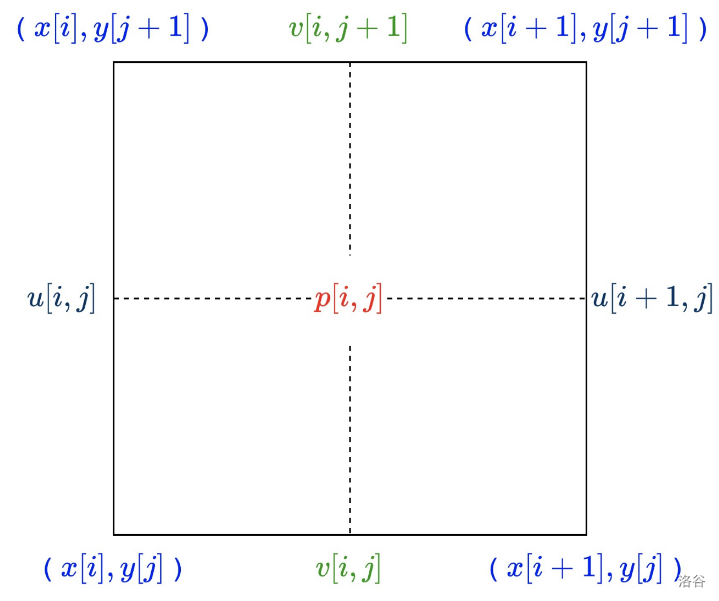
我们采取前向 Euler 格式:
$$\frac{\vec u^{n+1}-\vec u^n}{\Delta t}=-\frac1\rho\nabla^2p^{n+1}-\vec u^n\cdot\nabla\vec u^n+\nu\nabla^2\vec u^n$$
我们不知道压力 $p$ 是什么东西,所以先假设 $p$ 全是 $0$,先得到一个 $\vec u^\ast$:
$$\frac{\vec u^\ast-\vec u^n}{\Delta t}=-\vec u^n\cdot\nabla\vec u^n+\nu\nabla^2\vec u^n$$
这一步称为预测步。
然后考虑压力 $p$ 的影响:
$$\frac{\vec u^{n+1}-\vec u^\ast}{\Delta t}=-\frac1\rho\nabla p^{n+1}$$
显然,$u^{n+1}$ 应满足 $\nabla\cdot u^{n+1}=0$,所以我们对上式同时点乘 $\nabla$:
$$\nabla\cdot\frac{\vec u^{n+1}-\vec u^\ast}{\Delta t}=-\frac1\rho\nabla^2p^{n+1}$$
$$\nabla^2p^{n+1}=\frac\rho{\Delta t}\nabla\cdot\vec u^\ast$$
解出 $p^{n+1}$ 后代回去就可以得到 $\vec u^{u+1}$ 了。
这一步称为矫正步。
还有一个问题:知道 $\nabla^2p^{n+1}$ 后怎么求 $p^{n+1}$ 呢?
我们先离散,然后就变成了一个线性方程组,直接求解即可。
当然这个东西有亿点点小细节,我来说一下实现细节:
1. $L_x,L_y$ 表示模拟的范围是 $2\times2$ 的。
2. $n_x,n_y$ 表示有 $n_x\times n_y$ 个单元格。
3. $x_i$ 表示第 $i$ 列单元格的左边的横坐标。
4. $xm_i$ 表示第 $i$ 列单元格的中心的横坐标。
5. $y_j$ 表示第 $j$ 行单元格的底边的纵坐标。
6. $ym_j$ 表示第 $j$ 行单元格的中心的纵坐标。
7. $u_{i,j}$ 表示 $(x_i,ym_j)$ 处 $x$ 方向流速。
8. $v_{i,j}$ 表示 $(xm_i,y_j)$ 处 $y$ 方向流速。
9. $p_{i,j}$ 表示 $(xm_i,ym_j)$ 处的压强。
当然你不需要存 $xm_i,ym_i$。
然后照着上面的算就行了。
还有一种方法。
我们考虑一个函数 $f(x,v,t)$,表示位置 $x$,速度 $v$,时间 $t$ 的粒子密度,显然我们有:
$$\rho(x,t)=\int f(x,v,t)$$
$$\rho(x,t)u(x,t)=\int vf(x,v,t)$$
好,那么我们似乎应该有:
$$\frac{\partial f}{\partial t}+v\nabla f=0$$
但是,这个方程没有考虑粒子的碰撞,所以我们在右边再加一个碰撞项:
$$\frac{\partial f}{\partial t}+v\nabla f=\Omega[f]$$
这个东西叫 Boltzmann 方程,那么碰撞项 $\Omega[f]$ 是什么呢?我们给出 BGK 模型。
我们考虑,各种速度的粒子密度分布应该符合高斯分布,所以我们有:
$$f^{eq}(v)=\frac\rho{2\pi c_s^2}\exp\left(-\frac{|v-u|^2}{2c_s^2}\right)$$
其中 $u$ 是宏观速度,就是用上面 $$\rho(x,t)u(x,t)=\int vf(x,v,t)$$ 计算出来的速度。
那么我们就可以定义碰撞项了:
$$\Omega[f]=-\frac1\tau(f-f^{eq})$$
其中 $\tau$ 叫做弛豫时间。
那么显然,如果 $\tau$ 降低,动粘滞率就越小,实际上,我们有:
$$\mu=c_s^2\left(\tau-\frac12\right)$$
那么我们就需要对上式进行离散。
速度和时间我们就不说了,关键是速度。
我们在二维平面上选 $9$ 个方向:
$$c_0=c\begin{bmatrix}0\\0\end{bmatrix}$$
$$c_1=c\begin{bmatrix}1\\0\end{bmatrix}$$
$$c_2=c\begin{bmatrix}0\\1\end{bmatrix}$$
$$c_3=c\begin{bmatrix}-1\\0\end{bmatrix}$$
$$c_4=c\begin{bmatrix}0\\-1\end{bmatrix}$$
$$c_5=c\begin{bmatrix}1\\1\end{bmatrix}$$
$$c_6=c\begin{bmatrix}-1\\1\end{bmatrix}$$
$$c_7=c\begin{bmatrix}-1\\-1\end{bmatrix}$$
$$c_8=c\begin{bmatrix}1\\-1\end{bmatrix}$$
其中 $c$ 是格子边长。
这样我们需要更改一下 $f^{eq}(v)$:
$$f^{eq}(c_i)=\omega_i\rho\left[1+\frac{c_i\cdot u}{c_s^2}+\frac{(c_i\cdot u)^2}{2c_s^4}-\frac{u^2}{2c_s^2}\right]$$
其中 $\omega_i=\begin{cases}\frac49&|c_i|=0\\\frac19&|c_i|=c\\\frac1{36}&|c_i|=\sqrt2c\end{cases}$。
边界怎么处理?有两种情况。
一种是固定的边界,比如这个:
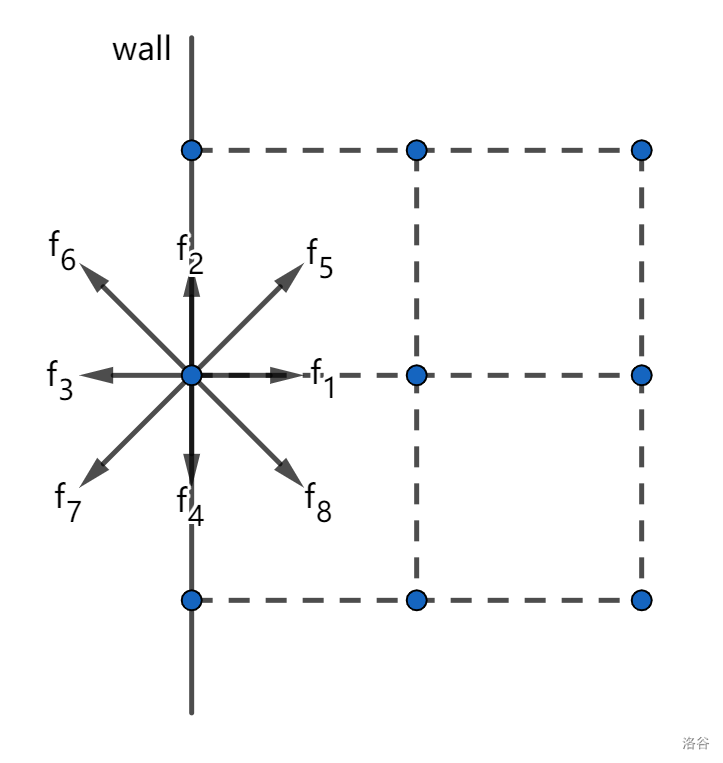
我们一般的假设就是一个粒子碰到边界会原路返回(别问我为什么不是反射),所以我们就有对于这个点 $f_5=f_7,f_1=f_3,f_8=f_6$。
lingyizhonh
那么就可以给出算法流程了:
1. 初始化:$f(x)=f^{eq}(x),\rho(x)=1,u(x)=0$。
2. 迭代过程:
3. 计算宏观量、平衡态 $f^{eq}$。
4. 计算碰撞(collision)。
5. 计算传播(streaming)。
6. 处理边界。
Code:
```cpp
#include <cstdio>
using namespace std;
const int Nx = 40;
const int Ny = 40;
const double Lx = 2;
const double Ly = 2;
const double dx = Lx / Nx;
const double dy = Ly / Ny;
const double dt = 0.001;
const double rho = 1;
const double nu = 0.1;
double x[Nx + 2], y[Ny + 2];
double u[Nx + 2][Ny + 2], v[Nx + 2][Ny + 2];
double us[Nx + 2][Ny + 2], vs[Nx + 2][Ny + 2];
double p[Nx + 1][Ny + 1];
void update_u() {
for (int i = 0; i < Nx + 2; i++) {
for (int j = 0; j < Ny + 2; j++) {
us[i][j] = u[i][j];
}
}
double delta;
for (int i = 2; i <= Nx; i++) {
for (int j = 1; j <= Ny; j++) {
delta = 0;
delta += nu * (u[i - 1][j] - 2 * u[i][j] + u[i + 1][j]) / (dx * dx);
delta += nu * (u[i][j - 1] - 2 * u[i][j] + u[i][j + 1]) / (dy * dy);
delta += -u[i][j] * (u[i + 1][j] - u[i - 1][j]) / (2 * dx);
delta += -(v[i][j] + v[i - 1][j] + v[i - 1][j + 1] + v[i][j + 1]) / 4 * (u[i][j + 1] - u[i][j - 1]) / (2 * dy);
us[i][j] += delta * dt;
}
}
}
void update_v() {
for (int i = 0; i < Nx + 2; i++) {
for (int j = 0; j < Ny + 2; j++) {
vs[i][j] = v[i][j];
}
}
double delta;
for (int i = 1; i <= Nx; i++) {
for (int j = 2; j <= Ny; j++) {
delta = 0;
delta += nu * (v[i - 1][j] - 2 * v[i][j] + v[i + 1][j]) / (dx * dx);
delta += nu * (v[i][j - 1] - 2 * v[i][j] + v[i][j + 1]) / (dy * dy);
delta += -v[i][j] * (v[i][j + 1] - v[i][j - 1]) / (2 * dy);
delta += -(u[i][j] + u[i + 1][j] + u[i + 1][j - 1] + u[i][j - 1]) / 4 * (v[i + 1][j] - v[i - 1][j]) / (2 * dx);
vs[i][j] += delta * dt;
}
}
}
double abs(double x) {
return x < 0 ? -x : x;
}
void correct() {
for (int i = 2; i <= Nx; i++) {
for (int j = 1; j <= Ny; j++) {
u[i][j] = us[i][j] - dt / rho * (p[i][j] - p[i - 1][j]) / dx;
}
}
for (int i = 1; i <= Nx; i++) {
for (int j = 2; j <= Ny; j++) {
v[i][j] = vs[i][j] - dt / rho * (p[i][j] - p[i][j - 1]) / dx;
}
}
}
double L[Nx * Ny][Nx * Ny], L_inv[Nx * Ny][Nx * Ny], R[Nx * Ny], pv[Nx * Ny];
int get_id(int i, int j) {
return i * Ny + j;
}
int get_i(int id) {
return id / Ny;
}
int get_j(int id) {
return id % Ny;
}
void swap(double & a, double & b) {
static double t;
t = a;
a = b;
b = t;
}
void init_L_inv() {
for (int i = 0; i < Nx; i++) {
for (int j = 0; j < Ny; j++) {
if (i == 0) {
L[get_id(i, j)][get_id(i, j)] += -1 / dx / dx;
L[get_id(i, j)][get_id(i + 1, j)] += 1 / dx / dx;
} else if (i == Nx - 1) {
L[get_id(i, j)][get_id(i - 1, j)] += 1 / dx / dx;
L[get_id(i, j)][get_id(i, j)] += -1 / dx / dx;
} else {
L[get_id(i, j)][get_id(i, j)] += -2 / dx / dx;
L[get_id(i, j)][get_id(i - 1, j)] += 1 / dx / dx;
L[get_id(i, j)][get_id(i + 1, j)] += 1 / dx / dx;
}
if (j == 0) {
L[get_id(i, j)][get_id(i, j + 1)] += 1 / dy / dy;
L[get_id(i, j)][get_id(i, j)] += -1 / dy / dy;
} else if (j == Ny - 1) {
L[get_id(i, j)][get_id(i, j - 1)] += 1 / dy / dy;
L[get_id(i, j)][get_id(i, j)] += -1 / dy / dy;
} else {
L[get_id(i, j)][get_id(i, j)] += -2 / dy / dy;
L[get_id(i, j)][get_id(i, j - 1)] += 1 / dy / dy;
L[get_id(i, j)][get_id(i, j + 1)] += 1 / dy / dy;
}
}
}
int n = Nx * Ny;
for (int i = 0; i < n; i++) {
L_inv[i][i] = 1;
}
for (int i = 0; i < n; i++) {
int main = i;
for (int j = i + 1; j < n; j++) {
if (abs(L[j][i]) > abs(L[main][i])) {
main = j;
}
}
if (abs(L[main][i]) < 1e-6) {
return;
}
for (int j = 0; j < n; j++) {
swap(L[main][j], L[i][j]);
swap(L_inv[main][j], L_inv[i][j]);
}
double temp = L[i][i];
for (int j = 0; j < n; j++) {
L[i][j] /= temp;
L_inv[i][j] /= temp;
}
for (int j = 0; j < n; j++) {
if (i != j && abs(L[j][i]) > 1e-6) {
temp = L[j][i];
for (int k = 0; k < n; k++) {
L[j][k] -= L[i][k] * temp;
L_inv[j][k] -= L_inv[i][k] * temp;
}
}
}
}
}
void calc_p() {
for (int i = 1; i <= Nx; i++) {
for (int j = 1; j <= Ny; j++) {
R[get_id(i - 1, j - 1)] = rho / dt * ((us[i + 1][j] - us[i][j]) / dx + (vs[i][j + 1] - vs[i][j]) / dy);
}
}
int n = Nx * Ny;
for (int i = 0; i < n; i++) {
p[get_i(i) + 1][get_j(i) + 1] = 0;
for (int j = 0; j < n; j++) {
p[get_i(i) + 1][get_j(i) + 1] += L_inv[i][j] * R[j];
}
}
}
void boundary_condition() {
for (int j = 0; j <= Nx; j++) {
u[1][j] = 0;
u[Nx + 1][j] = 0;
}
for (int i = 1; i <= Nx + 1; i++) {
u[i][0] = -u[i][1];
u[i][Ny + 1] = 2 - u[i][Ny];
}
for (int i = 0; i <= Nx + 1; i++) {
v[i][1] = 0;
v[i][Nx + 1] = 0;
}
for (int j = 1; j <= Ny; j++) {
v[0][j] = -v[1][j];
v[Nx + 1][j] = -v[Nx][j];
}
}
int main() {
freopen("output.txt", "w", stdout);
init_L_inv();
fprintf(stderr, "init_L_inv() done.\n");
for (int i = 0; i <= Nx; i++) {
x[i + 1] = Lx * i / Nx;
}
for (int j = 0; j <= Ny; j++) {
y[j + 1] = Ly * j / Ny;
}
for (int t = 0; t < 500; t++) {
boundary_condition();
update_u();
update_v();
calc_p();
correct();
fprintf(stderr, "t = %d done.\n", t);
}
for (int i = 0; i <= Nx + 1; i++) {
for (int j = 0; j <= Ny + 1; j++) {
printf("%lf ", u[i][j]);
}
printf("\n");
}
printf("\n");
for (int i = 0; i <= Nx + 1; i++) {
for (int j = 0; j <= Ny + 1; j++) {
printf("%lf ", v[i][j]);
}
printf("\n");
}
printf("\n");
for (int i = 0; i <= Nx + 1; i++) {
for (int j = 0; j <= Ny + 1; j++) {
printf("%lf ", p[i][j]);
}
printf("\n");
}
printf("\n");
return 0;
}
```