字符串
yzy4090
·
2023-07-18 11:53:17
·
个人记录
字符串本质上就是多了点数位的数字。反过来,数字就是少了点字母的字符串。
KMP 模式匹配
引入
KMP 模式匹配可以对于两个字符串 A,B ,在 O(|A|+|B|) 的时间复杂度下判断 A 是否是 B 的子串,并求出 A 在 B 中每次出现的位置。B 的每个位置,检查 B 的一个子串与 A 的哈希值是否相同。这个做法的时间复杂度也是线性的,但无法获得更多信息,因为哈希时已经将字符串模糊化为一个数字了。此处不详细介绍)O(|A||B|) 。它的主要问题是每次失败后都要重新进行匹配。
可以发现,当暴力还在计算 P_1 与 T_2 的关系时(此处下标从 1 开始),KMP 算法已经从第一轮枚举中知道 P_{1-2}=T_{3-4} ,并且 P_1\ne T_2 ,所以 KMP 可以直接从 P_3 和 T_5 处开始比对。那么如何做到知道接下来应该比对哪里呢?这就是 next 数组要做的事情了。
步骤
KMP 算法分为如下两步:
对 A 自我匹配,求出 next 数组,其中 next_i 表示 A 中以 i 结尾的非前缀子串与 A 的前缀能够匹配的最长长度。
对 A 和 B 匹配,求出 f 数组,其中 f_i 表示 B 中以 i 结尾的子串与 A 的前缀能够匹配的最长长度。
这个算法看似治标不治本,因为暴力算 next 数组的时间复杂度还是 O(|A|^2) 的。但是 next 数组决定了下次应该回退到哪里,具体来说是回退到失配位之前最长公共前后缀对应的前缀后一位的地方。如图:
当发现 \tt c 与 \tt a (\tt a 也可以是模式串 P 的 P_3 )失配后,KMP 知道 \tt beabe 的最长公共前后缀(不包括自身)是 \tt be ,所以下次从 \tt be 后的 \tt a 开始比对。
在匹配前后缀时,如果扩展失败,就让指针 j 跳回 next_j ,直至 j=0 ;否则指针 j 加 1 。更新 next_i 的值,它的值即为 j 。代码如下:
for(int i=2,j=0;i<=nd;i++){
while(j>0&&d[i]!=d[j+1])j=Next[j];
if(d[i]==d[j+1])++j;
Next[i]=j;
}
```cpp
for(int i=1,j=0;i<=nc;i++){
while(j>0&&(j==nd||c[i]!=d[j+1]))j=Next[j];
if(c[i]==d[j+1])++j;
if(j==nd)ans[++all]=i-nd+1;//完全匹配
}
```
## [最小表示法](https://www.luogu.com.cn/problem/P1368)
对于这样的环上问题,第一步是环断为链,复制成两倍长度。观察比较两个表示法的过程:
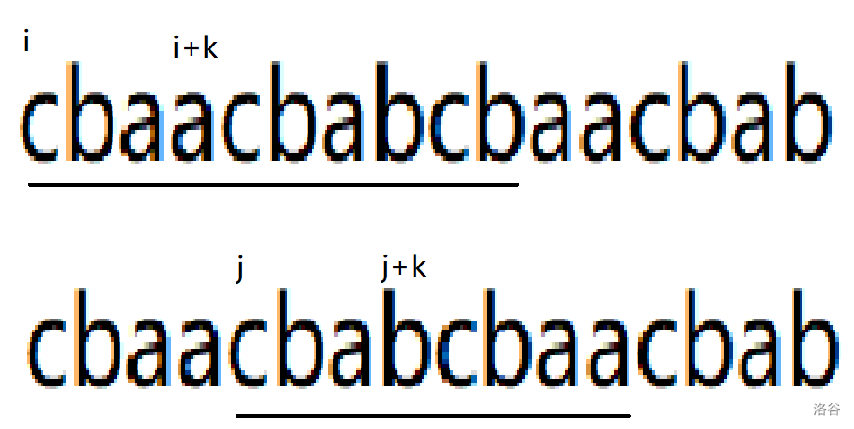
当 $S'_{i+k}>S'_{j+k}$ 时,则说明 $b_{i-i+k}$ 均不是 $S$ 的最小表示(证明比较浅显,可以看[此处](https://wenku.baidu.com/view/0e1a6013a216147917112820.html?_wkts_=1689658585795))。当 $S'_{i+k}<S'_{j+k}$ 时同理。于是有如下代码:
```cpp
#include<bits/stdc++.h>
using namespace std;
int n,a[600005];
int main() {
scanf("%d",&n);
for(int i=1; i<=n; i++)
scanf("%d",&a[i]),a[n+i]=a[i];
int i=1,j=2,k;
while(i<=n&&j<=n) {
for(k=0; k<n&&a[i+k]==a[j+k]; k++);
if(k==n)break;
if(a[i+k]>a[j+k]) {
i=i+k+1;//跳过不优的表示法
if(i==j)i++;
} else {
j=j+k+1;//同理
if(i==j)j++;
}
}
for(int ans=min(i,j),i=0; i<n; ans++,i++)
printf("%d ",a[ans]);
return 0;
}
```
该算法的时间复杂度为 $O(n)$。
------------
巧妙字符串。
字符串哈希,不要使用模 $2^k$ 意义下的哈希,也尽量不要使用知名模数。
对于第一种,底数为奇数使用 `abbabaabbaababba`,偶数使用 $64$ 个 `a`,还可以拼在一起,奇偶兼卡;第二种,出题人想卡就卡,随机一个字符串,挑出哈希值相同的,放到 hack 数据中。详情见[此处](https://blog.csdn.net/m0_46209312/article/details/105635114)。
不想被卡的话,应使用多模哈希(双模其实足矣),而不是模 $2^k$ 意义下的多底哈希,底数也应该神奇一些。
ACAM 和 PAM,后面的 AM 指的是自动机,就是一个指针在有向图上走,走到最后如果停在好位置就接受了。理论上来说,trie 和 KMP 也可以称作自动机。
比如 PAM 中向前走的边组成两棵 trie,因为奇偶回文串要分开(或者像 Manacher 合到一起),走回去的边是最长回文后缀,也就是 fail 指针。
fail 指针是说明“如果不能向前走了,去哪里的价值最大”的东西,和 KMP 中的 Border 数组很类似。
KMP 和 ACAM 的匹配是中途走到好位置,最后的位置用处不大。
PAM 最后的位置的深度指的是以当前字符为结尾的回文串个数(顺序插入)。
求以一个字符结尾最长的回文串长度除了可以直接使用 PAM 外,还可以用 Manacher+线段树解决。
字典树的最直观用处是对多个字符串同时比较,不同的今后就不再讨论。于是就有了 Apollo 一题和 ACAM,使之可以同时处理多个字符串。
Manacher 和 Z 函数的代码很像,这是因为它们都使用到了之前计算出的最有价值(或者说涵盖的东西最多)的东西。
```cpp
void Z(string str,int len){
int l=0,r=0;//未来最有价值的区间
z[1]=len;
for(int i=2;i<=len;i++){
if(i<=r)z[i]=min(z[i-l+1],r-i+1);
while(i+z[i]<=len&&str[z[i]+1]==str[i+z[i]])++z[i];
if(i+z[i]-1>r)l=i,r=i+z[i]-1;
}
}
```
在匹配什么上可以做些手脚,比如 Antisymmetry 是 0 匹配 1,1 匹配 0。
失配树上求 LCA 是对跳 Border 的改进。似乎 fail 指针也可以。
对于求 SA,我知道的有四种算法:倍增+基排,[DC3](https://wenku.baidu.com/view/5b886b1ea76e58fafab00374.html),SA-KA,SA-IS([1](https://riteme.site/blog/2016-6-19/sais.html) [2](https://vcode28629.github.io/SA-IS/))。
第一种其实是对朴素做法的一点改进:从逐个比较转变为 1 个,2 个,4 个......跳着比,如果有相同的就继续。
后面三种都是先算一小部分 SA,然后推出其它的东西。SA-KA 在算小部分时使用基排,SA-IS 使用诱导排序,差距并不大,但性能上以 SA-IS 为优。DC3 是算 2/3 推 1/3,常数大。
关于 height 数组,有巧妙引理:$height_{rk_i}\ge height_{rk_{i-1}}-1$。证明可见[此处](https://oi-wiki.org/string/sa/#on-%E6%B1%82-height-%E6%95%B0%E7%BB%84%E9%9C%80%E8%A6%81%E7%9A%84%E4%B8%80%E4%B8%AA%E5%BC%95%E7%90%86)。
[模板代码](https://www.luogu.com.cn/paste/vj4lf3r2)
[此处](https://wenku.baidu.com/view/0dc03d2b1611cc7931b765ce0508763230127479.html?_wkts_=1708222555033)证明了一些有关 height 数组的优美性质。