高中数学笔记 - 其他知识

· · 学习·文化课

数学笔记全文

修订

平面几何

Menelaus 梅涅劳斯定理

\frac{AF}{FB}\frac{BD}{DC}\frac{CE}{EA}=1

第一角元形式：\frac{\sin\angle ACF}{\sin\angle FCB}\frac{\sin\angle BAD}{\sin\angle DAC}\frac{\sin\angle CBE}{\sin\angle EBA}=1

第二角元形式：\frac{\sin\angle AOF}{\sin\angle FOB}\frac{\sin\angle BOD}{\sin\angle DOC}\frac{\sin\angle COE}{\sin\angle EOA}=1

Ceva 塞瓦定理

\frac{AF}{FB}\frac{BD}{DC}\frac{CE}{EA}=1

第一角元形式：\frac{\sin\angle ACF}{\sin\angle FCB}\frac{\sin\angle BAD}{\sin\angle DAC}\frac{\sin\angle CBE}{\sin\angle EBA}=1

第二角元形式：\frac{\sin\angle AOF}{\sin\angle FOB}\frac{\sin\angle BOD}{\sin\angle DOC}\frac{\sin\angle COE}{\sin\angle EOA}=1

Stewart 定理

AD^2=\frac{AC^2\cdot BD+AB^2\cdot DC}{BC}-BD\cdot DC

中线长公式：m_a^2=\frac{1}{2}AB^2+\frac{1}{2}AC^2-\frac{1}{4}BC^2

角平分线长公式：t_a=AB\cdot AC-BD\cdot DC=\frac{2}{AB+AC}\sqrt{AB\cdot AC\cdot p\cdot(p-BC)},p=\frac{AB+BC+CA}{2}

调和点列

定义：若 \displaystyle\frac{AC}{CB}=\frac{AD}{DB}，则称 (A,B,C,D) 为调和点列，C,D 调和分割线段 A,B。

性质：以下设 M 为 AB 中点。

  2. AB\cdot CD=2AD\cdot BC=2AC\cdot DB
  3. CA\cdot CB=CM\cdot CD$，$DA\cdot DB=DM\cdot DC
  4. MA^2=MB^2=MC\cdot MD

内切圆和调和点列

由梅涅劳斯定理得 \frac{AF}{FB}\frac{BG}{GC}\frac{CE}{EA}=1，又因为 AF=AE,BF=BD,CE=CD，

得 \frac{BD}{CD}=\frac{BG}{CG}\implies(B,D,C,G) 为调和点列。

极线和调和点列

# 线性规划 ### 例题 1 $$\begin{cases}5x-11y \geq -22 \\ 2x+3y \geq 9 \\ 2x \leq 11\end{cases}$$ $z = 10x + 10y, \max{z} = \ ?

基本概念

  1. 约束条件：变量 x,y,\dots 满足的一组条件，上述二元一次不等式组就是对 x,y 的约束条件。
  2. 线性约束条件：由变量 x,y,\dots 的一次不等式 / 方程组成的不等式组就称为线性约束条件，如上述二元一次不等式。
  3. 目标函数：欲求最大值或最小值所涉及的变量 x,y,\dots 的解析式，如上述 z。
  4. 线性目标函数：目标函数关于变量 x,y,\dots 的一次解析式，如上述 z。
  5. 线性规划问题：在线性约束条件下求线性目标函数的问题。
  6. 可行解：满足线性约束条件的解 (x,y)。
  7. 可行域：由所有可行解组成的集合。
  8. 最优解：使目标函数取得 \max 或 \min 的可行解。

解法

  1. 画图，数形结合。

    \begin{cases}5x-11y \geq -22 & \implies y \leq \frac{5}{11}x + \frac{1}{2} & \implies & y = \frac{5}{11}x + \frac{1}{2}\ 图像的下边 \\ 2x+3y \geq 9 & \implies y \geq -\frac{2}{3}x + 3 & \implies & y = -\frac{2}{3}x + 3\ 图像的上边 \\ 2x \leq 11 & \implies x \leq \frac{11}{2} & \implies & x=\frac{11}{2}\ 图像的左边 \end{cases}

    在平面直角坐标系上画出对应的平面区域 （ 可行域 ），再把目标函数 z=ax+by 变形为 y=-\frac{a}{b}x + \frac{z}{b}，\\ 所以求 z 的最值可看成是求直线 y=-\frac{a}{b}x + \frac{z}{b} 在 y 轴上截距的最值。以这题为例，\\ z=10x+10y \implies y= -x + \frac{z}{10} 容易证明，当 z=85 时 y 轴上截距取最值，所以 \max{z}=85.

  2. 仔细观察，可以发现最优解非常容易出现在可行域构成的多面体的顶点处。

例题 2

\begin{cases}y \geq x \\ x + y \leq 2 \\ x \geq a\end{cases} (2x+y)_{\mathrm{max}}=4(2x+y)_{\mathrm{min}},\ a=\ ?

例题 3（ 2024 九省联考 T14 ）

\begin{cases} 0<a<b<c<1 \\ b\geq 2a \ \ \ \mathrm{or}\ \ \ a+b\leq 1 \end{cases} \max{\set{b-a,c-b,1-c}}$ 的最小值 $=\ ? \max{\set{b-a,c-b,1-c}}\geq\max{\set{b-a,\frac{1-b}{2}}} $$\begin{cases}0<x \\ x<y \\ y<1 \\ y\geq 2x\ \ \ \mathrm{or}\ \ \ x+y\leq 1\end{cases}$$ - 作出可行域：$\mathrm{and}$ 连接的区域之间取交，$\mathrm{or}$ 连接的区域之间取并。阴影部分即为可行域。 $\ \ \ \ \ \ \text{}$ 图中 $y\geq 2x\ \ \ x+y\leq 1$ 两条解析式用红色标出。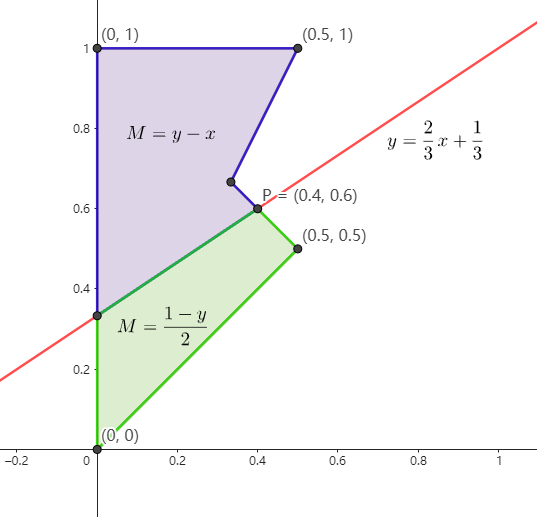 ![](https://cdn.luogu.com.cn/upload/image_hosting/0uvhhx28.png) - 回到题目，要求 $M=\max{\set{y-x,\frac{1-y}{2}}}$，我们需要知道何时 $M=y-x$，何时 $M=\frac{1-y}{2} ![](https://cdn.luogu.com.cn/upload/image_hosting/0hyhebem.png) - 因为最终要求的是 $M$ 的最小值，所以对蓝色区域而言，$y$ 尽量小，$x$ 尽量大，根据例题 1 的经验，这样的极值点通常出现在多边形的顶点处，经过比较后 $P$ 点是极值点，此时 $M=0.2$。对绿色区域而言，只需满足 $y$ 尽量大，显然，$P$ 点也是极值点。 - 综上所述，$\max{\set{b-a,c-b,1-c}}$ 的最小值 $=\frac{1}{5}$。 # 数论 因为这里是数学笔记，不是 OI 笔记，因此只有一些简要的定理。 ## 质数 - 定义：一个正整数无法被除了 $1$ 和它自身之外的任何自然数整除，则成为质数，否则为合数。 - 数量：对于一个足够大的整数 $N$，不超过 $N$ 的质数有 $\pi(x)\approx\frac{N}{\ln N}$ 个，所以第 $n$ 个质数约为 $n\ln n$。 - 判定：试除法，若 $N$ 为合数，则存在一个能整除 $N$ 的数 $T$ 且 $2 \leq T \leq \sqrt{N}$。 - 算数基本定理：$N = p_1^{c_1}p_2^{c_2}\dots p_n^{c_n}$，$N$ 的正约数个数 $=\displaystyle\prod_{i=1}^{n}(c_i+1)$， $N$ 的所有正约数的和 $=\displaystyle\prod_{i=1}^{n}(\displaystyle\sum_{j=0}^{c_i}(p_i)^j)$。 一个正整数 $N$ 的约数个数上界为 $2\sqrt{N}$，$1$ ~ $N$ 每个数的约数个数的总和大约为 $N\log N$。 ## 因数 ### 整除 若 $b$ 能整除 $a$，则记为 $a\mid b$，如 $2\mid 12$。若 $b$ 不能整除 $a$，则记为 $a\nmid b$，如 $5\nmid 12$。 若 $a\nmid b$，则 $b\div a$ 存在余数 $r$ 且 $0<r<a$，记 $r=a\ \mathrm{mod}\ b$。例如，$3\ \mathrm{mod}\ 2=1$。 整除具有以下性质： 1. 若 $a\mid b$ 且 $a\mid c$，则 $\forall x,y$，有 $a\mid xb+yc$。 2. 若 $a\mid b$ 且 $b\mid c$，则 $a\mid c$。 3. 若 $a\mid b$ 且 $b\mid a$，则 $a=\pm b$。 4. 设 $m\neq 0$，则 $a\mid b$，当且仅当 $ma\mid mb$。 ### 最大公因数与最小公倍数 设 $a,b$ 是两个不为 $0$ 的整数，能使 $d\mid a$ 和 $d\mid b$ 成立的最大整数 $d$，称为 $a,b$ 的最大公因数，记作 $\gcd(a,b)$。 设 $a,b$ 是两个不为 $0$ 的整数，能使 $a\mid d$ 和 $b\mid d$ 成立的最小整数 $d$，称为 $a,b$ 的最小公倍数，记作 $\mathrm{lcm}(a,b)$。 - $\forall a,b\in\N,\ \gcd(a,b)\cdot\mathrm{lcm}(a,b)=ab

证明：设 d=\gcd(a,b),a_0=\frac{a}{d},b_0=\frac{b}{d}。根据最大公因数的定义，有 \gcd(a_0,b_0)=1。\\\ \ \ \ \ \ \ \ \ \text{} 再根据最小公倍数的定义，有 \mathrm{lcm}(a,b)=a_0\cdot b_0。\\\ \ \ \ \ \ \ \ \ \text{} 于是 \mathrm{lcm}(a,b)=\mathrm{lcm}(a_0\cdot d,b_0\cdot d)=\mathrm{lcm}(a_0,b_0)\cdot d=a_0\cdot b_0\cdot d=\frac{a\cdot b}{d}，原命题得证。

证明：d\mid a,d\mid b\implies d\mid(a-b)。

证明：分类讨论。

  1. 若 a<b，则有 \gcd(b,a\ \mathrm{mod}\ b)=\gcd(b,a)=\gcd(a,b)。
  2. 若 a\geq b，不妨设 a=q\cdot b+r\ (0\leq r<b)。显然 r=a\ \mathrm{mod}\ b。对于 a,b 的任意公因数 d，\\ 因为 d\mid a,d\mid q\cdot b，故 d\mid (a-q\cdot b)，即 d\mid r。因此 d 也是 b,r 的公因数，反之亦成立。\\ 故 a,b 的公因数集合与 b,a\ \mathrm{mod}\ b 的公因数集合相同。于是它们的最大公因数也相等。

欧拉函数

若 $N = p_1^{c_1}p_2^{c_2}\dots p_n^{c_n}$，则 $\varphi(N)=N\times\frac{p_1-1}{p_1}\times\frac{p_2-1}{p_2}\times\dots\times\frac{p_n-1}{p_n}=N\cdot\displaystyle\prod_{质数p|N}(1-\frac{1}{p})

证明：设 p,q 为 N 的不同质因子，1 ~ N 中 p 的倍数有 N\over p 个，q 的倍数有 N \over q 个。若把 \frac{N}{p}+\frac{N}{q} 个数去掉，则 \frac{N}{pq} 被计算了 2 次（ 容斥原理 ）。因此， 1 ~ N 中不与 N 含有相同质因子的 p 或 q 数量为 \\ N-\frac{N}{p}-\frac{N}{q}+\frac{N}{pq}=N(1-\frac{1}{p})(1-\frac{1}{q})，对 N 的全部质因子继续容斥即可得到公式。

n 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
\varphi(n) 1 1 2 2 4 2 6 4 6 4 10 4 12 6 8

欧拉函数的性质：

  2. 若 a,b 互质，则 \varphi(ab)=\varphi(a)\varphi(b)。
  3. 设 p 为质数，\varphi(p)=p-1。
  4. 设 p 为质数，k\in\N^*,\varphi(p^k)=p^{k-1}\times(p-1)=p^k-p^{k-1}。
  5. 设 p 为质数，若 p\mid n 且 p^2\mid n，则 \varphi(n)=\varphi(\frac{n}{p})\times p。
  6. 设 p 为质数，若 p\mid n 但 p^2\nmid n，则 \varphi(n)=\varphi(\frac{n}{p})\times (p-1)。
  7. 若 n 为奇数，则 \varphi(2n)=\varphi(n)。
  9. 欧拉反演：\displaystyle\sum_{d\mid n}\varphi(d)=n。

证明：

  1. 因为 \gcd(n,x)=\gcd(n,n-x)，所以与 n 不互质的数 x,n-x 成对出现，平均值为 \frac{n}{2}。\\ 因此与 n 互质的数的平均值也是 \frac{n}{2}，进而得到性质 1。
  2. 根据欧拉函数的计算式可直接获得性质 2。
  3. 根据欧拉函数的定义可直接获得性质 3。
  4. 从 1 ~ p^{k} 中的所有数，除了 p^{k-1} 个 p 的倍数外都与 p^k 互素。
  5. 若 p\mid n 且 p^2\mid n，则 n,\frac{n}{p} 包含相同的质因子，只是 p 的指数不同。\\ 按照欧拉函数的计算公式，\frac{\varphi(n)}{\varphi(\frac{n}{p})}=\frac{n}{\frac{n}{p}}=p，得到性质 5。
  6. 若 p\mid n 且 p^2\mid n，则 n,\frac{n}{p} 互质。因为 \varphi(n)=\varphi(\frac{n}{p})\varphi(p)，而 \varphi(p)=p-1，得到性质 6。
  9. 设 f(n)=\displaystyle\sum_{d\mid n}\varphi(d)，利用 \varphi 是积性函数，得到：\\若 n,m 互质，则 f(nm)=\displaystyle\sum_{d\mid nm}\varphi(d)=\displaystyle\sum_{d\mid n}\varphi(d)\cdot\displaystyle\sum_{d\mid m}\varphi(d)=f(n)f(m)，即 f(n) 是积性函数。\\ 对于单个质因子有：\begin{aligned}f(p^m)&=\displaystyle\sum_{d\mid p^m}\varphi(d)=\displaystyle\sum_{i=0}^{m}\varphi(p^i)=\varphi(1)+\varphi(p)+\varphi(p^2)+\varphi(p^3)+\dots+\varphi(p^m)\\&= 1+(p-1)+(p-1)p+(p-1)p^2+\dots+(p-1)p^{m-1}\\&=1+(p-1)+(p^2-p)+(p^3-p^2)+\dots+(p^m-p^{m-1})=p^m\end{aligned} \\ 所以 f(n)=\displaystyle\prod_{i=1}^{m}f(p_i^{c_i})=\displaystyle\prod_{i=1}^{m}p_i^{c_i}=n

积性函数与完全积性函数

若函数 f(x) 满足 f(1)=1 且 \forall x,y\in\N^{*},\gcd(x,y)=1 都有 f(xy)=f(x)f(y)，则 f(x) 是积性函数。

若函数 f(x) 满足 f(1)=1 且 \forall x,y\in\N^{*} 都有 f(xy)=f(x)f(y)，则 f(x) 是完全积性函数。

性质：

  1. 若 f(x) 和 g(x) 均为积性函数，则以下函数也为积性函数： \begin{aligned}h(x)&=f(x^p) \\ h(x)&=f^p(x) \\ h(x)&=f(x)g(x) \\ h(x)&=\displaystyle\sum_{d\mid x}f(d)g(\frac{x}{d})\end{aligned}

  2. 设 x=\displaystyle\prod p_i^{c_i}，

    若 f(x) 为积性函数，则 f(x)=\displaystyle\prod f(p_i^{c_i})。

    若 f(x) 为完全积性函数，则 f(x)=\displaystyle\prod f^{c_i}(p_i)。

例子：

积性函数：\varphi(n),\sigma _k(n)=\displaystyle\sum_{d\mid n}d^k,\sigma _0(n) 通常简记为 d(n) 或 \tau(n)，\sigma _1(n) 通常简记为 \sigma(n)。

完全积性函数：\varepsilon(n)=[n=1],\text{id}_k(n)=n^k,\text{id}_1(n) 通常简记为 \text{id}(n),f(n)=1。

同余

费马小定理与欧拉定理

若整数 a 和整数 b 除以正整数 m 的余数相等，则称 a,b 模 m 同余，记为 a\equiv b\ (\mathrm{mod}\ m)。

并且注意到 k\ \mathrm{mod}\ i=k-\lfloor\frac{k}{i}\rfloor\cdot i，且同余满足同加性、同乘性、同幂性，但不满足同除性。

对于 \forall a \in [0, m - 1]，集合 \set{a+km\ (k\in\Z)} 的所有数模 m 同余，余数都是 a。该集合称为一个模 m 的同余类，简记为 \overline{a}。

模 m 的同余类一共有 m 个，分别为 \overline{0},\overline{1},\overline{2},\dots,\overline{m-1}。它们构成 m 的完全剩余系。

若从某个非空数集中任选两个元素（ 同一元素可重复选出 ），选出的这两个元素通过某种（ 或几种 ）运算后的得数仍是该数集中的元素，那么，就说该集合对于这种（ 或几种 ）运算是封闭的。$\\$例如若一个集合中的元素，如果能够做到做加法运算的结果还在这个集合中，就说这个集合对加法运算封闭。$\\$ 例如 $\N$ 对加法、乘法运算是封闭的；$\Z$ 对加、减、乘法运算是封闭的；$\mathbb{Q}, \mathbb{C}$ 对四则运算是封闭的。 简化剩余系关于模 $m$ 乘法封闭。这是因为若 $a,b\ (1\leq a,b\leq m)$ 与 $m$ 互质，则 $ab$ 也与 $m$ 互质。$\\$由余数的定义得 $ab\ \mathrm{mod}\ m$ 也与 $m$ 互质，即 $ab\ \mathrm{mod}\ m$ 也属于 $m$ 的简化剩余系。 - 费马小定理：若 $p$ 是质数，则对于任意整数 $a$，有 $a^p\equiv a\ (\mathrm{mod}\ p)$。 - 欧拉定理：若正整数 $a,n$ 互质，则 $a^{\varphi(n)}\equiv 1\ (\mathrm{mod}\ n)$。 证明：设 $n$ 的简化剩余系为 $\set{\overline{a_1},\overline{a_2},\dots,\overline{a_{\varphi(n)}}}$。$\forall a_i,a_j$，若 $a\cdot a_i\equiv a\cdot a_j\ (\mathrm{mod}\ n)$，则 $a\cdot(a_i-a_j)\equiv 0\\$ 因为 $a,n$ 互质，所以 $a_i\equiv a_j$。故当 $a_i\neq a_j$ 时，$aa_i,aa_j$ 也代表不同的同余类。 又因为简化剩余系关于模 $m$ 乘法封闭，故 $\overline{aa_1}$ 也在简化剩余系集合中。因此，集合 $\set{\overline{a_1},\overline{a_2},\dots,\overline{a_{\varphi(n)}}}$ 与集合 $\set{\overline{aa_1},\overline{aa_2},\dots,\overline{aa_{\varphi(n)}}}$ 都能表示 $n$ 的简化剩余系。综上所述： $$a^{\varphi(n)}a_1a_2\dots a_{\varphi(n)}\equiv(aa_1)(aa_2)\dots(aa_{\varphi(n)})\equiv a_1a_2\dots a_{\varphi(n)}\ (\mathrm{mod}\ n)$$ 因此 $a^{\varphi(n)}\equiv 1\ (\mathrm{mod}\ n)$。当 $p$ 为质数时，满足 $\varphi(p)=p-1$，两边同乘 $a$ 即可得到费马小定理。 另外，当 $a$ 是 $p$ 的倍数，费马小定理显然成立。 --- - 欧拉定理的推论：若正整数 $a,n$ 互质，则对于任意正整数 $b$，有 $a^b\equiv a^{b\ \mathrm{mod}\ \varphi(n)}\ (\mathrm{mod}\ n)

证明：设 b=q\cdot \varphi(n)+r，其中 0\leq r<\varphi(n)，即 r=b\ \mathrm{mod}\ \varphi(n)。于是有：

a^b\equiv a^{q\cdot\varphi(n)+r}\equiv (a^{\varphi(n)})^q\cdot a^r\equiv 1^q\cdot a^r\equiv a^r\equiv a^{b\ \mathrm{mod}\ \varphi(n)}\ (\mathrm{mod}\ n)

证毕。面对 a+b,a-b,a\cdot b 这样的算式，可以在计算前先把 a,b 对 p 取模。面对 a^b 这样的乘方算式，可以先把底数对 p 取模、指数对 \varphi(p) 取模，再计算乘方。

即 a^b\equiv (a\ \mathrm{mod}\ p)^{b\ \mathrm{mod}\ \varphi(p)}\ (\mathrm{mod}\ p)

反证法，假设满足 a^x\equiv 1\ (\mathrm{mod}\ n) 的最小正整数 x_0 不能整除 \varphi(n)。

设 \varphi(n)=qx_0+r\ (0<r<x_0)，因为 a^{x_0}\equiv 1\ (\mathrm{mod}\ n)，所以 a^{qx_0}\equiv 1\ (\mathrm{mod}\ n)。根据欧拉定理 a^{\varphi(n)}\equiv 1\ (\mathrm{mod}\ n)，所以 a^r\equiv 1\ (\mathrm{mod}\ n)。这与 x_0 最小矛盾。故假设不成立，原命题成立。

中国剩余定理

设 m_1,m_2,\dots,m_n 是两两互质的整数，m=\displaystyle\prod_{i=1}^n m_i,M_i=\frac{m}{m_i},t_i 是线性同余方程 M_it_i\equiv 1\ (\mathrm{mod}\ m_i) 的一个解。对于任意的 n 个整数，方程组

\begin{cases}x\equiv a_1\ (\mathrm{mod}\ m_1) \\ x\equiv a_2\ (\mathrm{mod}\ m_2)\\ \ \ \ \ \ \ \ \ \ \ \ \ \vdots\\ x\equiv a_n\ (\mathrm{mod}\ m_n)\end{cases}

有整数解，解为 x=\displaystyle\sum_{i=1}^{n}a_iM_it_i，通解可以表示为 x+km(k\in\Z)，最小非负整数解为 x\ \mathrm{mod}\ m。

证明：因为 M_i=\frac{m}{m_i} 是除了 m_i 之外所有模数的倍数，所以 \forall k\neq i,a_iM_it_i\equiv 0\ (\mathrm{mod}\ m_i)，\\ \ \ \ \ \ \ \ \ \ \ \text{}所以代入 x=\displaystyle\sum_{i=1}^{n}a_iM_it_i，原方程组成立。

威尔逊定理

证明：

  1. 充分性

    对于 p 不是素数的情况，有 \begin{cases} p=1 & (1-1)!\equiv 0\ (\mathrm{mod}\ 1) \\ p=4 & (4-1)!\equiv 2\ (\mathrm{mod}\ 4) \\ p>4 & 分类讨论得出\ (p-1)!\equiv 0\ (\mathrm{mod}\ p) \end{cases}

    (a) 当 p 为完全平方数。

    则 p=k^2 且 k>2，用相减法比较 2k 与 p 的大小得 2k<p，于是有

    \begin{aligned}(p-1)!&=1\times 2\times\dots\times k\times\dots\times 2k\times\dots\times (p-1)\\ &=2nk^2\\&=2np\end{aligned}

    所以 (p-1)!\equiv 0\ (\mathrm{mod}\ p) 且 p 为完全平方数。

    (b) 当 p 不为完全平方数。

    则 p 可以表示为两个不相等的数 a 和 b 的乘积，设 a<b，则有 p=ab,1<a<b<p

    \begin{aligned}(p-1)!&=1\times 2\times\dots\times a\times\dots\times b\times\dots\times (p-1)\\&=a\times b\times n\\ &=np\end{aligned}

    所以 (p-1)!\equiv 0\ (\mathrm{mod}\ p) 且 p 不为完全平方数。

  2. 必要性

    当 p 为素数时，考虑二次剩余式 x^2\equiv 1\ (\mathrm{mod}\ p)，化简得 (x-1)(x+1)\equiv 0\ (\mathrm{mod}\ p)

    于是 x\equiv 1\ (\mathrm{mod}\ p) 或 x\equiv p-1\ (\mathrm{mod}\ p)。现在先抛开 1 和 p-1 不管，

    \forall a\in [2,p-2]$，必然存在一个和它不相等的逆元 $a^{-1}\in[2,p-2]$，满足 $aa^{-1}\equiv 1\ (\mathrm{mod}\ p)

    所以必然有 \frac{p-3}{2} 对数相乘的乘积为 1，即 (p-2)!\equiv 1\ (\mathrm{mod}\ p)

    等式两边同时乘 p-1 就得到威尔逊定理。

例题：n\in\N^* 且 n\leq 10^6，求 S_n。

S_n=\displaystyle\sum_{k=1}^{n}\lfloor\frac{(3k+6)!+1}{3k+7}-\lfloor\frac{(3k+6)!}{3k+7}\rfloor\rfloor

令 d=3k+7，原式化简为

S_n=\displaystyle\sum_{k=1}^{n}\lfloor\frac{(d-1)!+1}{d}-\lfloor\frac{(d-1)!}{d}\rfloor\rfloor

由威尔逊定理，当 d 为素数时，\frac{(d-1)!+1}{d} 必然是整数，而 \lfloor\frac{(d-1)!}{d}\rfloor 必然比 \frac{(d-1)!+1}{d} 小 1，于是有：

\begin{cases}p\ 为素数 & \lfloor\frac{(d-1)!+1}{d}-\lfloor\frac{(d-1)!}{d}\rfloor\rfloor=1 \\ p\ 为合数 & \lfloor\frac{(d-1)!+1}{d}-\lfloor\frac{(d-1)!}{d}\rfloor\rfloor=0\end{cases}

所以只需统计 [1,3\times 10^6+7] 中的素数即可得出答案。

牛顿迭代

对于在 [a,b] 上连续且单调的函数 f(x)，牛顿迭代法可用于求解方程 f(x)=0 的近似解。

初始时先从给定的 f(x) 和近似解 x_0 开始，x_0 可以是随机数。然后我们可以得到 f(x_0)。

接着，画出与 f(x) 切于点 (x_0,f(x_0)) 的直线 l_0，将 l_0 与 x 轴的交点横坐标记为 x_1，x_1 就是更优的近似解。

重复这个迭代过程，可以得到：

f'(x_i)=\frac{f(x_i)}{x_i-x_{i+1}} \implies x_{i+1}=x_i-\frac{f(x_i)}{f'(x_i)}

优点：收敛率是平方级别的，这意味着每次迭代后近似解的精确数位会翻倍。

缺点：不能处理重复的根；解可能在拐点附近发散；解可能在局部极小值或最大值附近振荡；当斜率接近于零时，解可能发散或到达不同的根。

拉格朗日插值法

由 n 个点可以唯一确定一个多项式 y=f(x)（不含 \log, a^x）, 当已知这 n 个点的坐标要求 f(k) 有：

f(k)=\displaystyle\sum_{i=1}^{n}y_i(\displaystyle\prod_{i\neq j}^{1\leq j\leq n}\frac{k-x_j}{x_i-x_j})

如果已知 f(1),f(2),\dots,f(n),f(n+1)，要求 f(x) 有：

f(x)=\displaystyle\sum_{i=1}^{n+1}(-1)^{n+1-i}\cdot y_i\cdot\frac{\displaystyle\prod_{j=1}^{n+1}(x-j)}{(i-1)!(n+1-i)!(x-i)}