高精度
luckydrawbox
·
·
算法·理论
头文件
此模板涉及的头文件较多,建议用 <bits/stdc++.h> 库。
强制转换
此模板支持两种转换:
定义
定义时直接用强制转换类型赋值即可。
设置变量类型
第一行是这样的一个代码:
#define T long long
请根据情况选择,类型将会影响接下来的压位。
## 设置压位
在 $\text{BigInteger}$ 类的 $\text{private}$ 部分中有这个代码:
```cpp
static const T base = 10000;
static const int width = 4;
```
设你需要压的位为 $x$ 位,把 ``base = 10000`` 中的 $10000$ 改成 $10^x$,把 ``width = 4`` 中的 $4$ 改成 $x$。
当然位数也是有限制的,你要保证 $10^{2x}$ 不超过 $T$ 的范围,例如 $\text{long long}$ 最多只能有 $9$ 位。
## 操作
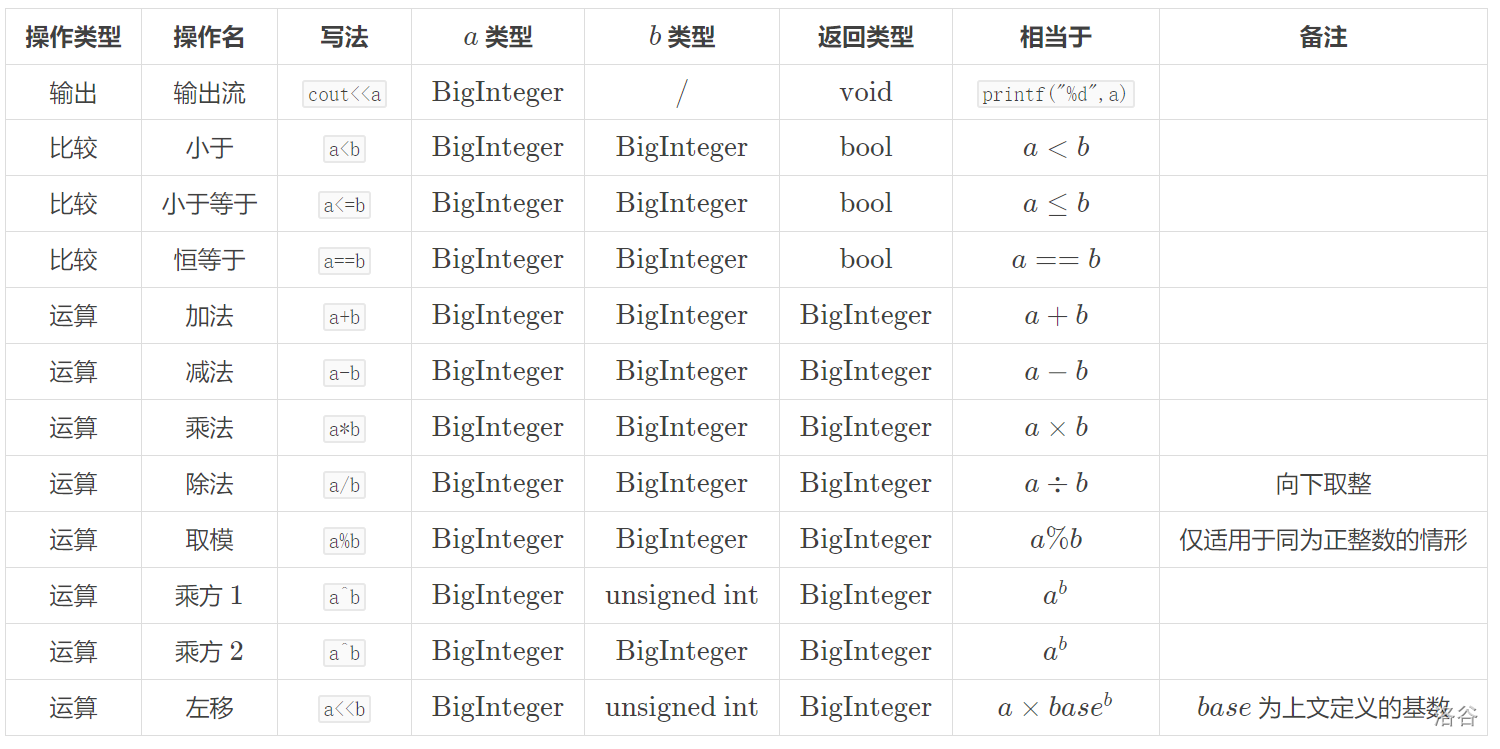
输出流和左移运算可能会造成歧义,如果你想输出 $a\times base^b$,不能这么写:
```cpp
cout<<a<<b;
```
应该加上括号:
```cpp
cout<<(a<<b);
```
## 代码
```cpp
#define T long long
// 常量,分别表示正数、负数、相等。
const int POSITIVE = 1, NEGATIVE = -1, EQUAL = 0;
class BigInteger
{
// 重载输出符号。
friend ostream& operator<<(ostream&, const BigInteger&);
// 比较操作。
friend int compare(const BigInteger&, const BigInteger&);
friend bool operator<(const BigInteger&, const BigInteger&);
friend bool operator<=(const BigInteger&, const BigInteger&);
friend bool operator==(const BigInteger&, const BigInteger&);
// 相关运算的实现:加法、减法、乘法、除法、模、乘方、左移。
friend BigInteger operator+(const BigInteger&, const BigInteger&);
friend BigInteger operator-(const BigInteger&, const BigInteger&);
friend BigInteger operator*(const BigInteger&, const BigInteger&);
friend BigInteger operator/(const BigInteger&, const BigInteger&);
friend BigInteger operator%(const BigInteger&, const BigInteger&);
friend BigInteger operator^(const BigInteger&, const unsigned int&);
friend BigInteger operator^(const BigInteger&, const BigInteger&);
friend BigInteger operator<<(const BigInteger&, const unsigned int&);
public:
BigInteger() {};
// 将长整型及字符串转换为高精度整数的构造函数。
BigInteger(const T&);
BigInteger(const string&);
// 获取高精度整数的最后一个数位值。
T lastDigit() const { return digits.front(); }
~BigInteger() {};
private:
// 清除运算产生的前导零。
void zeroJustify(void);
static const T base = 1000000;
static const int width = 6;
// 符号位和保存数位的向量。
T sign;
vector<T> digits;
T stoi(string s)
{
T ans=0;
int l=s.size();
for(int i=0;i<l;i++){
ans*=10;
ans+=s[i]-'0';
}
return ans;
}
};
// 移除无效的前导零。
void BigInteger::zeroJustify(void){
for (int i = digits.size() - 1; i >= 1; i--)
{
if (digits[i] > 0)
break;
digits.erase(digits.begin() + i);
}
if (digits.size() == 1 && digits[0] == 0)
sign = POSITIVE;
}
// 重载输出符号以输出大整数。
ostream& operator<<(ostream& os, const BigInteger& number){
os << (number.sign > 0 ? "" : "-");
os << number.digits[number.digits.size() - 1];
for (int i = (int)number.digits.size() - 2; i >= 0; i--)
os << setw(number.width) << setfill('0') << number.digits[i];
return os;
}
// 将长整型数转换为大整数。
BigInteger::BigInteger(const T& value){
if (value == 0)
{
sign = POSITIVE;
digits.push_back(0);
}
else
{
// 不断模基数取余得到各个数位。
sign = (value >= 0 ? POSITIVE : NEGATIVE);
T number = abs(value);
while (number)
{
digits.push_back(number % base);
number /= base;
}
}
// 移除前导零。
zeroJustify();
};
// 将十进制的字符串转换为大整数。
BigInteger::BigInteger(const string& value){
if (value.length() == 0)
{
sign = POSITIVE;
digits.push_back(0);
}
else
{
// 设置数值的正负号。
sign = value[0] == '-' ? NEGATIVE : POSITIVE;
//转换为整数存储到数位数组中。
string block;
for (int index = value.length() - 1; index >= 0; index--)
{
if (isdigit(value[index]))
block.insert(block.begin(), value[index]);
if (block.length() == width)
{
digits.push_back(stoi(block));
block.clear();
}
}
if (block.length() > 0)
digits.push_back(stoi(block));
}
// 移除前导零。
zeroJustify();
}
// 比较两个高精度整数的大小。
// x 大于 y,返回 1,x 小于 y,返回-1,x 等于 y,返回 0。
// 为了后续除法的需要调整了实现,使得对于未经前导零调整的整数也能够得到正确的处理。
int compare(const BigInteger& x, const BigInteger& y){
// 符号不同,正数大于负数。
if (x.sign == POSITIVE && y.sign == NEGATIVE ||
x.sign == NEGATIVE && y.sign == POSITIVE)
return (x.sign == POSITIVE ? 1 : -1);
// 确定 x 和 y 的有效数位个数,前导零不计入有效数位。
int xDigitNumber = x.digits.size() - 1;
for (; xDigitNumber && x.digits[xDigitNumber] == 0; xDigitNumber--) ;
int yDigitNumber = y.digits.size() - 1;
for (; yDigitNumber && y.digits[yDigitNumber] == 0; yDigitNumber--) ;
// 符号相同,同为正数,数位个数越多则越大,同为负数,数位个数越多则越小。
if (xDigitNumber > yDigitNumber)
return (x.sign == POSITIVE ? 1 : -1);
// 符号相同,同为正数,数位个数越少则越小,同为负数,数位个数越少则越大。
if (xDigitNumber < yDigitNumber)
return (x.sign == NEGATIVE ? 1 : -1);
// 符号相同,数位个数相同,逐位比较。
for (int index = xDigitNumber; index >= 0; index--)
{
if (x.digits[index] > y.digits[index])
return (x.sign == POSITIVE ? 1 : -1);
if (x.digits[index] < y.digits[index])
return (x.sign == NEGATIVE ? 1 : -1);
}
// 两数相等。
return 0;
}
// 等于比较运算符。
bool operator==(const BigInteger& x, const BigInteger& y){
return compare(x, y) == 0;
}
// 小于比较运算符。
bool operator<(const BigInteger& x, const BigInteger& y){
return compare(x, y) < 0;
}
// 小于等于比较运算符。
bool operator<=(const BigInteger& x, const BigInteger& y){
return compare(x, y) <= 0;
}
// 高精度整数加法。
BigInteger operator+(const BigInteger& x, const BigInteger& y){
BigInteger z;
// 如果两个加数的符号不同,转换为减法运算。
if (x.sign == NEGATIVE && y.sign == POSITIVE)
{
z = x;
z.sign = POSITIVE;
return (y - z);
}
else if (x.sign == POSITIVE && y.sign == NEGATIVE)
{
z = y;
z.sign = POSITIVE;
return (x - z);
}
// 确保 x 的位数比 y 的位数多,便于计算。
if (x.digits.size() < y.digits.size())
return (y + x);
// 两个加数的符号相同时才进行加法运算。预先为结果分配存储空间。
z.sign = x.sign + y.sign >= 0 ? POSITIVE : NEGATIVE;
z.digits.resize(max(x.digits.size(), y.digits.size()) + 1);
fill(z.digits.begin(), z.digits.end(), 0);
// 逐位相加,考虑进位。
int index = 0;
T carry = 0;
for (; index < x.digits.size(); index++)
{
// 获取对应位的和。
T sum = x.digits[index] + carry;
sum += index < y.digits.size() ? y.digits[index] : 0;
// 确定进位。
carry = sum / z.base;
// 将和保存到结果的相应位中。
z.digits[index] = sum % z.base;
}
// 保存最后可能产生的进位。
z.digits[index] = carry;
// 移除前导零。
z.zeroJustify();
return z;
}
// 高精度整数减法。
BigInteger operator-(const BigInteger& x, const BigInteger& y){
BigInteger z;
// 当 x 和 y 至少有一个是负数,转换为加法运算。
if (x.sign == NEGATIVE || y.sign == NEGATIVE)
{
z = y;
z.sign = -y.sign;
return x + z;
}
// 都为正数,确保 x 大于 y,便于计算。
if (x < y)
{
z = y - x;
z.sign = NEGATIVE;
return z;
}
// 设置符号位并预先分配存储空间。
z.sign = POSITIVE;
z.digits.resize(max(x.digits.size(), y.digits.size()));
fill(z.digits.begin(), z.digits.end(), 0);
// 逐位相减,考虑借位。
int index = 0;
T borrow = 0;
for (; index < x.digits.size(); index++)
{
// 获取对应位的差。
T difference = x.digits[index] - borrow;
difference -= index < y.digits.size() ? y.digits[index] : 0;
// 确定是否有借位。
borrow = 0;
if (difference < 0)
{
difference += z.base;
borrow = 1;
}
// 保存相应位差的结果。
z.digits[index] = difference % z.base;
}
// 移除前导零。
z.zeroJustify();
return z;
}
// 高精度整数乘法。
BigInteger operator*(const BigInteger& x, const BigInteger& y){
BigInteger z;
// 设置符号位并预先分配存储空间。
z.sign = x.sign * y.sign;
z.digits.resize(x.digits.size() + y.digits.size());
fill(z.digits.begin(), z.digits.end(), 0);
// 一行一行相乘然后相加。
for (int i = 0; i < y.digits.size(); i++)
for (int j = 0; j < x.digits.size(); j++)
{
z.digits[i + j] += x.digits[j] * y.digits[i];
z.digits[i + j + 1] += z.digits[i + j] / z.base;
z.digits[i + j] %= z.base;
}
// 移除前导零。
z.zeroJustify();
return z;
}
// 高精度整数除法,为整除运算。
BigInteger operator/(const BigInteger& x, const BigInteger& y){
// z 表示整除得到的商,r 表示每次试除时的被除数。
BigInteger z, r;
// 设置商和被除数的符号位。
z.sign = x.sign * y.sign;
r.sign = POSITIVE;
// 为商 z 和表示被除数的 r 预先分配存储空间。
z.digits.resize(max(1,(int)(x.digits.size() - y.digits.size() + 1)));
r.digits.resize(y.digits.size() + 1);
// 初始化值。
fill(z.digits.begin(), z.digits.end(), 0);
fill(r.digits.begin(), r.digits.end(), 0);
// 从高位到低位逐位试除得到对应位的商。
for (int i = x.digits.size() - 1; i >= 0; i--)
{
// 获取被除数,将上一次未被除尽的余数的移到高位加上当前数位继续除。
r.digits.insert(r.digits.begin(), x.digits[i]);
// 通过二分试除法得到对应位的商。
T low = 0, high = z.base - 1, middle = (high + low + 1) >> 1;
while (low < high)
{
if ((y * BigInteger(middle)) <= r)
low = middle;
else
high = middle - 1;
middle = (high + low + 1) >> 1;
}
// 执行减法,从被除数中减去指定数量的 y。
for (int index = 0; index < y.digits.size(); index++)
{
T difference = r.digits[index] - middle * y.digits[index];
// 确定是否有借位产生。
T borrow = 0;
if (difference < 0)
borrow = (z.base - 1 - difference) / z.base;
// 高位减去借位数量。
r.digits[index + 1] -= borrow;
// 低位加上借位。
difference += z.base * borrow;
r.digits[index] = difference % z.base;
}
// 将对应位的商存入结果中。
z.digits.insert(z.digits.begin(), middle);
}
// 移除前导零。
z.zeroJustify();
return z;
}
// 高精度整数求模运算。适用于同为正整数的情形。
BigInteger operator%(const BigInteger& x, const BigInteger& y){
return (x - (x / y) * y);
}
// 高精度整数乘方运算,乘法次数为内置整数类型。
BigInteger operator^(const BigInteger& x, const unsigned int& y){
if (y == 0)
return BigInteger(1);
if (y == 1)
return x;
if (y == 2)
return x * x;
if (y & 1 > 0)
return ((x ^ (y / 2)) ^ 2) * x;
else
return ((x ^ (y / 2)) ^ 2);
}
const BigInteger ZERO = BigInteger(0), ONE = BigInteger(1), TWO = BigInteger(2);
// 高精度整数乘方运算,乘方次数为高精度整数。
BigInteger operator^(const BigInteger& x, const BigInteger& y){
if (y == ZERO)
return BigInteger(1);
if (y == ONE)
return x;
if (y == TWO)
return x * x;
if (y.lastDigit() & 1 > 0)
return ((x ^ (y / 2)) ^ 2) * x;
else
return ((x ^ (y / 2)) ^ 2);
}
// 高精度整数左移运算,左移一位相当于将此数乘以基数。
BigInteger operator<<(const BigInteger& x, const unsigned int& shift){
BigInteger z;
// 设置符号位,复制向量中的数据。
z.sign = x.sign;
z.digits.resize(x.digits.size());
copy(x.digits.begin(), x.digits.end(), z.digits.begin());
// 移动指定位数,补零。
for (int i = 0; i < shift; i++)
z.digits.insert(z.digits.begin(), 0);
// 移除前导零。
z.zeroJustify();
return z;
}
```
[back](https://www.luogu.com.cn/article/dltjrzaa)