CSP 初赛计算机科学部分的知识总结

MilkyCoffee · 2020-08-08 20:27:36 · 个人记录

update on 6-13 : 搭配提高组初赛通过指南食用味道更佳！

update on 6-16 : 更名为，初赛计算机科学部分的知识总结与整理。

大家好呀，本博文是为了要冲省一的奆老们写的，很多奆老OI水平很高，但是普及组初赛会考一些其他的知识，而且这些知识零零散散的，让我们来整理一下。

在 CSP 或 NOIp 中，选择题会进行计算机科学方面的考察。本文之前

这篇博文只是列举了知识点，如果要练习的话，按照下面的顺序：

从 2020 年初赛开始倒序刷题
如果嫌题不够，可以去刷信息学奥赛一本通--初赛篇（不建议弱省的同学进行练习，因为弱省初赛过有手就行（？）
初赛不计入最后的算分和评分之内，所以初赛包过就行，最重要的还是复赛刷题。

注意！请不要认为初赛只考这些，与 OI 相关的会考很多。

计算机常识

IT : Information Technology 信息技术

代别	年代	逻辑（电子）原件
第一代	1946~1958	电子管
第二代	1959~1964	晶体管
第三代	1965~1970	集成电路
第四代	1971~至今	大规模、超大规模集成电路

根据性能指标来分类，可以将计算机分成：巨型机、大型机、中型机、小型机、微型机和工作站

巨型机：超级计算机，运算快，容量大，主要用于顶尖科研领域（银河、顶点（美）、山脊（美）、神威•天湖之光、天河二）

大、中型机：国家级科研机构、中点院校使用。

小型机：一般科研机构、学校使用

微型机：家用计算机（PC机、个人计算机）运用最为广泛，70年代之后开始普及。

工作站：性能更高的微型机，主要用于图形、图像处理、计算机辅助设计。

计算机应用：

计算机拥有快速性、通用性、准确性和逻辑性等特点。

科学计算：在科研、工程等领域完成大量复杂的计算。计算机的基本应用
信息处理：对数据进行收集、存储、整理、分类、统计、加工、利用、传播等活动。计算机主要应用
自动控制：利用计算机及时采集、检测数据，按照最优值迅速控制对象进行自动调节、自动控制。
计算机辅助技术：利用计算机帮助人们设计、处理
人工智能：利用计算机模拟人类的智能活动
网络应用：利用计算机进行网络相关活动

关于空间转换

$1024B = 1KB

1024KB = 1MB

1024MB = 1GB

1024GB = 1TB

这点要记牢，基本每年都会考，没啥好说的，背就是了。

关于计算机的常识性问题

第一台计算机：ENIAC

第一位程序猿：Ada Lovelace

艾伦•图灵（英），是计算机科学之父，冯•诺依曼（美籍匈牙利），是计算机之父，千万要记牢，考场上不能忘。有一项以图灵命名的奖项：图灵奖，这是计算机领域最高的奖项，1948年，克劳德·香农将热力学中的熵引入信息通信领域，标志着信息论研究的开端。

提出存储程序控制原理的人是冯诺依曼

关于硬件的“常识性”问题

计算机构成：运算器、控制器、存储器、输入设备、输出设备

CPU由运算器（算数、逻辑运算）、控制器（指挥系统）和一些寄存器构成。

CPU为微型计算机的核心部件。

存储器：保存各类程序的数据信息，包括主存储器（内存储器）和辅助存储器

主存储器（内存储器）：简称内存，和CPU一起构成的部分可以被CPU直接访问。

RAM：内容根据需要随时输入输出，也可以随时重新写入，但是一旦停电，RAM里的信息会全部丢失

ROM：只能读出而不能写入和修改，断电后信息不会消失

CPU历史：出现于 20 世纪 70 年代，字长 4-8-16-32-644−8−16−32−64 位。

CPU访问速度：寄存器>高速缓存>内存>外存断电后保留数据于 ROM和外存这一点有可能考，哪个不是CPU的主要性能指标。 - 扩展名 .jpeg .png 等为图像存储方式 .mp4 等为视频存储方式 .mp3 等为音频存储方式 - 关于计算机语言的常识性问题机器语言：计算机最早的语言，计算机能直接识别的语言。用二进制数来编写，所以又被成为二进制语言。优点：速度快。缺点：难度大汇编语言：开始用符号代替二进制数，比机器语言简单。但是计算机不能直接识别，需要特殊软件进行翻译。汇编语言仍属于低级语言，依旧难写，现在已经很少被人使用。高级语言：现在人们使用的OI语言（Basic、Pascal、PHP、C、C++、C#、python等） 1. 编译方式：先将代码交给翻译程序翻译成机器语言，然后连接可执行程序。 2. 解释方式：边扫描边解释，扫描一句解释一句，不再同一翻译。（PHP、Basic、python等）编码：计算机除了处理数值数据之外，还要处理符号、图形、图像、声音等数据。由于计算机智能识别0和1，所以需要将这些信息转化为0和1。这一过程就是编码（"翻译"的意思）。数据：能被计算机接收并处理的符号的集合被称为数据。比特：一个二进制数，计算机表示信息的数据编码中的最小单位。字节：八个比特构成一个字节。存储系统中的最小单位。 - 关于ASCII的常识性问题 ACSII码是美国国家交换标准代码（现为世界交换代码标准）。一种7位二进制编码（**占用一个字节**），用于表示128个国际通用字符。 1. 数字'0'~'9'（48~57） 2. 26个英文字母（大写：65~90；小写：97~122） 3. 通用符号如 +-*/ 等32个 4. 控制符号（空格、回车等） - 关于字符排序方式。汉字交换码：使用类似于ACSII码的方式，一级汉字拼音排序，二级汉字部首排序。字形存储码：使用点阵来表示汉字图形（$16*16*24*24$） - 关于病毒的常识性知识计算机病毒（主要针对软件系统）在计算机运行过程中，能把自身精确拷贝到或有修改的拷贝到其他程序体内的程序。特征：隐蔽性、潜伏性、传播性、激发性、破坏性、危害性。传播方式：网络和硬盘 - 关于机器数与真值在计算机中，表示数值的符号只有0和1，我们规定最高位为符号位，并用0表示正号，1表示负号，这样，计算机中的数值和符号就都全“数码化”。例如：-0000001 -> 10000001 01010101 -> 101010101 为了简化机器中数据的运算字符，人们采用原码、反码和补码等方法对数值和数字同一编码。原码：直接用符号和真值表示。例如：x=01010101，$[x]_{yuan}$ = 001010101 反码：正数的反码就是正数本身（符号位为0），负数的反码对符号位以外的数字“求反”（0变1，1变0）例如：x=-1100110 $[x]_{fan}$ = 10011001 补码：正数的补码就是正数本身（符号位为0），负数的补码是符号位为1，数值各取其反，最低位+1 - 关于IP的尝试 1. IPv4 点分十进制，每部分取值 $0 $~$255$，注意，这里IPv4的结构大概是： 12.35.185.54 注意，每个都不能大于255（除了主机ID（第一位）其他都能是0或255）， 2. IPv6 冒号十六进制，共128位二进制。这个是为了防止IPv4不够用了，只需要知道这一点就行了。 - 计算机网络利用通信线路和设备，将不同地方的计算机连接起来。 TCP/IP:用于网络的一组通信协议。网络的主要功能：资源共享、信息传输、分布处理、综合信息服务。 - 关于一些缩写注：之前有几年考过哪个缩写所对应的释义是正确的。局域网 -- LAN // LAN和MAN一般都由多个LAN构成（一种在小范围内实现的计算机网络，一般在1km的范围内，局域网内传输效率极高，误码率低，结构简单容易实现）城域网 -- MAN （城域网的范围大概在几千米至几十千米内）广域网 -- WAN （广域网的范围大概几十千米到几千千米以上） - 从网络的拓扑来看，域网一共可分为以下五类：星形、总线形、环形、树形、网状性（不规则性）其中星形结构最为简单容易管理维护，但可靠性较低。一般广域网使用网状性。随机存储器 -- RAM 只读存储器 -- ROM 因特网 -- Internet 万维网 -- WWW 文件传输协议 -- LFTP 远程登录 -- Telnet 超文本标记语言 -- HTML 超文本传输协议 -- HTTP 简单邮件传输协议 -- SMTP 邮局协议第三版 -- POP3 交互邮件访问协议 -- IMAP 传输控制协议 -- TCP 网际协议 -- IP 域名系统 -- DNS 统一资源定位器 -- URL - 关于 NOIp 考试本身 NOIp，全国青少年信息学奥林匹克联赛（省级），开办于1995年，截止2018已举办24届，2019年暂停，2020年恢复。 CSP 没有那么久远的历史自己考自己，所以没有列举。复赛使用C、C++、Pascal，2022年后只能使用C++。复赛评测系统：NOI Linux 广告：[本人写的NOI Linux系统介绍QAQ](https://www.luogu.com.cn/blog/317198/noi-linux-shi-yong-ji-tong-jie-shao) NOI，全国青少年计算机程序设计竞赛，开办于1984年，现更名全国青少年信息学奥林匹克竞赛。第37届NOI（2020年）在长沙举行。 APIO 亚洲与太平洋地区信息学奥林匹克竞赛 IOI 国际信息学奥林匹克竞赛 - 计算机软件语言分类（从低级——高级排列）：机器语言——汇编语言——高级语言。 ![](https://cdn.luogu.com.cn/upload/image_hosting/vob651gw.png) - 区间： [3, 5) : 大于等于3，小于5。 - 数学问题。建议复习，排列组合，进制问题（如进制的转换），方程还有最小公倍数、因数这方面的知识。 - 分辨率显示分辨率（屏幕分辨率）是屏幕图像的精密度，是指显示器所能显示的像素的多少。由于屏幕上的点、线和面都是由像素组成的，显示器可显示的像素越多，画面就越精细，同样的屏幕区域内能显示的信息也越多，所以分辨率是个非常重要的性能指标。显示分辨率一定的情况下，显示屏越小图像越清晰，反之，显示屏大小固定时，显示分辨率越高图像越清晰。比如说，设一台数码相机中CCD芯片的像素数目为300万，300万就是横着的像素×竖着的像素。 $x * y == 3000000$ （他的意思就是x\*y<=3000000），然后求出x和y（约等于多少，）就行了。也有给你图片的大小让你算出这个图片的KB、MB的。比如说，某张图片的分辨率为1024\*1024，是24位真彩色，要你算出这张图片占了多少MB。 $1024 * 1024 * 24 = 25165824$（bit） $25165824 / 1024 / 1024 / 8 = 3$（MB）也就是说这张图片占了3MB。 XX位真彩色（如24位真彩色）表示存储一个像素点需要24位bit。 ### 注：以下是 CSP-J / NOIp 普及组初赛考过的关于 OI 的常识性问题，一些想去考普及组的小朋友可以继续看，需要考 CSP-S / NOIp 的同学们可以去 [这里](https://www.luogu.com.cn/blog/317198/ti-gao-zu-chu-sai-tong-guo-zhi-na) 查看更多与 OI 相关的知识。 - 关于集合运算的常识（大部分人可略过） - 交 A $\cap$ B ![](https://cdn.luogu.com.cn/upload/image_hosting/smpwqnfu.png) 若一个元素在集合A中，也在集合B中，就激发条件A $\cap$ B - 并 A $\cup$ B ![](https://cdn.luogu.com.cn/upload/image_hosting/6vpc2jue.png) 若一个元素要么在A中，要么在B中，称为A $\cup$ B - 补 ~A或者 $\overline{A}

    ![](https://cdn.luogu.com.cn/upload/image_hosting/65bk0dds.png)

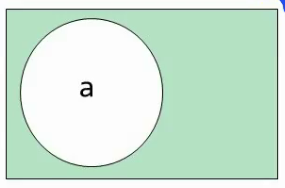
    不在A中，但是在A外面的所有元素都在A的补集中。

- 差

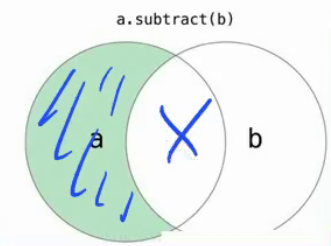
    ![](https://cdn.luogu.com.cn/upload/image_hosting/kiun0mp9.png)

    在A中而不能在B中，称为A的差集。

- 容斥原理

    对于有限集合S，用 |S| 表示 S 的元素个数

    设A，B为有限集合，则

    $$|A\ \cup B| = |A| + |B| - |A \ \cap B|$$

    设A，B，C为有限集合，则

    $$|A\ \cup B \cup C| = |A| + |B| + |C| - |B \ \cap C| - |A\ \cap B| - |A\ \cap C| + |A\ \cap B\ \cap C|$$

关于树的常识

结点的度 = 子结点个数

度 = 一个点的分叉个数

一个树的度 = max(所有结点的度)

总结点数 = 线的数 + 1
- 二叉树
  
  二叉树的定义：每个结点最多（注意）有两个结点（两个结点分别为，左子树和右子树）（俗名左儿子和右儿子）
  
  二叉树的遍历：
```
1. 先序遍历：根->左->右
2. 中序遍历：左->根->右
3. 后序遍历：左->右->根

这里会考，比如说给出先序遍历和中序遍历，让你求后序遍历
```
  - 满二叉树
    
    每个根有两个子树。
  - 完全二叉树
    
    每个根有两个子树，最后一行可以没有子树。
关于图
- 基本
  
  顶点(V) + 边(E) = 图(V, E)
  
  最基本的图（无向图）：
- 有向边
  
  如上图，若只能从A走到C而不能从C走到A，那么这条边为有向边
- 有向图
  
  define：全部为有向边的图为有向图
  
  入度：有向图中，以一个顶点为终点的有向边的数目。
  
  出度：有向图中，以一个顶点为起点的有向边的数目。
  
  有向图中每个顶点的度等于该顶点的入度与出度之和
- 无向图
  
  度：无向图中，与一个顶点相连的边的数目。
- 一些概念
  
  边权：边的价值，一般指边的长度。
  
  回路/环：起点与终点相同的路径。
  
  简单图：图中没有重边和自环
  
  顶点A到顶点B联通（无向）：直接或间接地经过若干条边，使得顶点A通向顶点B。
  
  顶点A到顶点B联通（有向）：直接或间接地经过若干条边（均为一个方向的有向边），使得顶点A通向顶点B。
  
  完全图：任意两个顶点之间存在边直达，完全无向图有n*(n-1)÷2条边，有向图有(n-1)*n条边。
  
  有向图中每个点的度是入度与出度之和。
  
  连通图：图中任意两个结点都是联通的。
- 遍历方式
  - 广度优先遍历。
    
    逐步入队相邻的所有未访问过的点。
  - 深度优先遍历
    
    从一个点出发，访问与之所有相连的点。
补充：
链表

插入删除不需要移动元素，不必事先估计存储空间，所需空间与线性表长度成正比

不可随机访问任一元素

后记

对于本文出现的学术性问题，本人十分抱歉。如果您发现了其中之一，请在下方留言告诉我。