学术社区
静静是他的,
·
·
个人记录
学习了 出题人题解
题意
每个消息有 $s_1, s_2, s_3$ 三个字符串。
- 楼下型消息:对于消息 $i$, 满足 $s_3 = \text{louxia}$,$s_{i, 2} = s_{i - 1, 1}$。
- 楼上型消息:对于消息 $i$, 满足 $s_3 = \text{loushang}$, $s_{i, 2} = s_{i + 1, 1}$。
每一个在帖子中发过言的人都一定会在帖子中发出至少一条学术消息。
#### 特殊性质 ABC
##### 特殊性质 A: 很好理解,只用考虑楼下型消息。
现在有只有 **学术消息** 和 **楼下型消息**。
对于楼下型消息 $(A, B, \text{louxia})$,能发现一个明显的指向关系。
对于多个楼下型消息,就是一串相连的关系。
因此,考虑把这些关系抽象成**有向图**,每一条关系可以将图上 $B$ 连向 $A$。
**经过一条边**的意义是选择这个消息,**停留在某点**的意义就是当前最后说话的人,**楼下型消息连边**的意义就是现在 $A$ 可以说话,下一个说话的人是 $B$, 才能选择当前消息。
##### 特殊性质 B: 每条楼下型消息得用。
求题目要求的最多消息个数,这里显然就是要把图中每条边都走一遍。
对于重排后的答案的样子,应该是:
- 学术消息 -> 楼下 -> 楼下 ... 学术消息 -> 楼下 ...
问题可以转化为,在图上任选一条路径 $(u, v)$, 并且 $u$ 点前还要有学术消息,在 $v$ 时停止,最后要把所有边覆盖。
##### 欧拉回路
覆盖所有边,可以考虑 **欧拉回路** 的算法。
- 合法的欧拉回路要满足: 任意点的 **入度等于出度**。
1. 首先对于学术消息 $(A, B,C)$。
建虚点 $T$, 并且 $T$ 向 $A$ 连一条边,表示当前最后说话的是 $A$。
2. 实际上,每个点的 **入度大于等于出度**。
这里**出度**可以理解为有多少条楼下消息,而**入度**理解为出度中的楼下消息可以选择的楼上,并且有这些能选。
性质B保证每个消息都有的选楼上。
3. 对于点 $A$, 出度小于入度,就连 $A$ 到 $T$ 的边,直到出度等于入度。
最后得到的路径方案就是合法方案。
随手画了个图:

两条红边就是加入的虚边。
可以发现选出来的,都是 $T \to A \to B ... \to T \to C ... \to T$ 这样的回路。
#### 特殊性质 AC
和 特殊性质ABC 的分析一样,但是没有保证楼下型消息都有用。
在图中出现的情况是:存在点 $A$ 的 **入度小于出度**。
按照上面的理解:
- **入度**理解为出度中的楼下消息可以选择的楼上。
那么就会有楼上型消息选不到它要求的楼上。
为了满足欧拉回路的要求,那么就从 $T$ 向 $A$ 连边,直到入度等于出度。
对于答案中的一段回路, 例如: $... \to T \to A \to B \to T \to ...$。
如果 $T \to A$ 是补充的虚边,那么 $A \to B$ 这条关系就不满足,因为 $A$ 并未发言。
图:

如图, $T \to D$ 是补充的虚边, 而 $D \to C$ 的不符合实际。
#### 特殊性质 BC
这时加入了楼上型消息。
对于一条楼上型消息 $(A, B, \text{loushang})$, 此时应该将 $A$ 连向 $B$。
因为和楼下型消息连边的意义差不多,当前 $A$ 可以说话,只有下一个人是 $B$ 这个消息才合法。
用一个图难以表示两种不同的类型,考虑分层图。
对于楼上型消息的图,称之为 $G_0$, 对于楼下型消息的图,称之为 $G_1$。
- 楼下型消息 $(A, B, \text{louxia})$, 在 $G_0$ 连 $B \to A$。
- 楼上型消息 $(A, B, \text{loushang})$, 在 $G_1$ 连 $A \to B$。
这时的学术消息可以在楼上型和楼下型消息之间做桥梁连接。
- 学术消息 $(A, B,C)$,在 $G_1$ 的 $A$ 连向 $G_0$ 的 $A$,简称 $A_1 \to A_0$。
特殊性质 B 保证:
- 在 $G_0$ 中 **入度大于等于出度**。
- 在 $G_1$ 中 **出度大于等于入度**。
$G_0$ 中, $A$ 连 **入度减出度** 条 $A -> T$。
$G_1$ 中, $A$ 连 **出度减入度** 条 $T -> A$。
这样就可以跑欧拉回路了。
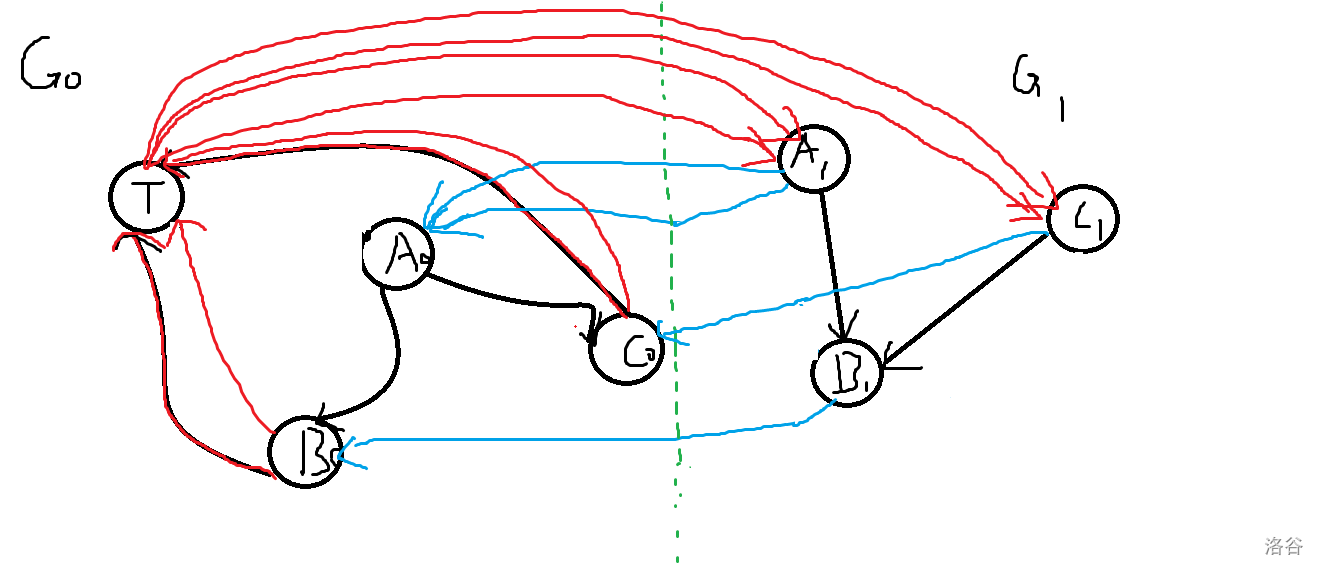
红边是补充边,蓝边是学术消息。
可以发现路径是 $T \to A_1 \to B_1 \to ... \to C_1 \to A_0 \to B_0 \to T \to ...
特殊性质 C
少了特殊性质 B, 就会有楼上型消息或楼下型消息配不上它要的楼上或楼下。
- 在 G_0 中表现为,存在点 A 的 入度小于出度。
- 在 G_1 中表现为,存在点 A 的 入度大于出度。
那么还不如当成学术消息利用,问题是怎么选出那些要变成学术消息?
-
在 G_0 中,如果存在点 A 的入度小于出度,那么有 出度-入度 条边用不上。
假设边是楼下型消息 B_0 \to A_0, 那么改成学术消息后就是 A_1 \to A_0。
这里的变化是 B_0 的出度减小 1, A_1 的出度增加 1。
对于点 B_0 和 A_1 用不到的消息都各自减少 1。
-
对于 G_1 也同理:
假设边是楼上型消息 A_1 \to B_1, 那么改成学术消息后就是 A_1 \to A_0。
这里的变化是 B_1 的入度减小 1, A_0 的入度增加 1。
对于点 A_0 和 B_1 用不到的消息都各自减少 1。
这就可以表示成一个网络流模型:
-
-
-
对于楼下型消息 (A, B, \text{louxia}), A_1 \to B_0, 流量是 1。
-
对于楼上型消息 (A, B, \text{loushang}), B_1 \to A_0, 流量是 1。
求最大流,网络流中剩余流量为 0的边表示的楼下楼上型消息,会变成学术消息。
但是仍然可能出现 G_0 入度小于出度的情况,就像特殊性质 AC 一样解决即可。
正解
发现特殊性质 C 没了后,楼上型消息 (A, B, \text{louxia}), 其实可以和楼下型消息 (B, A, \text{louxia}) 组合在一起, 这样总是不劣的。
这样的组合也能像学术消息一样在楼上型消息和楼下型消息之间。
可以在图中连 A_1 \to B_0。
这些组合就可以不用考虑了。
采用 特殊性质 C 的解法即可。
代码
每个子任务的代码都有, 由于太长了就放在剪贴板。
代码