【图论】树上差分 & 树上问题类
Audrey_Hall
·
·
算法·理论
例题
给定一棵 n 个节点的树,树有边权,有 m 次操作,每次查询给出两个节点,求他们在树上的距离。
Solution
当我们求出 x 和 y 的 LCA 后,发现可以把这个距离看做两段:
即 x 到 LCA和 y 到 LCA 的距离,
计算出 dep[i] 表示 i 节点的深度,
则 dep[x]-dep[lca] 可表示 x 到 LCA 的距离,
输出 dep[x]-dep[lca]+dep[y]-dep[lca] 即可。
树上差分
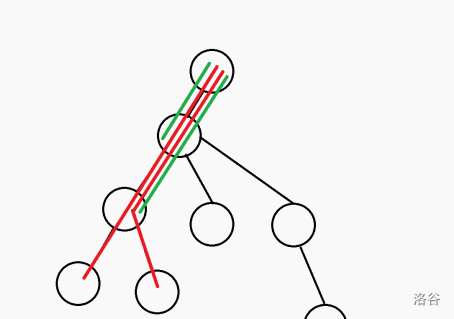
把 x 到 y 在树上的路径差分为:
$+y$ 到根的路径
$-$ LCA 到根的路径
$-$ LCA 的父亲到根的路径
***
**静态树上问题类**
dfs 序以及树上差分的思想非常重要,
这些树上问题一般离线后都会又快又好写,建议使用离线的写法,
难点主要在于分析问题的具体性质,难以概括,
如果查询是树上的路径信息,可以使用树上差分的方法。
**例题**
给定一个 $n$ 个点的树,有 $m$ 次查询,每次查 $x$ 到 $y$ 路径上的点权和。
Q:序列上没有修改的时候我们怎么求区间和呢?
A:利用前缀和差分。
Q:那树上呢?
A:利用树上前缀和差分即可。
总时间复杂度 $\text{O}(n+m)
给定一个 n 个点的树,有 m 次查询,每次给两个点 x,y,求 x,y 之间的距离。
考虑预处理出 dep[x] 表示 x 到根的距离,
则利用树上差分的方法,
$x$ 到 LCA 的距离就是 `dep[x]-dep[lca]`
总时间复杂度 $\text{O}(n+m)
给一个 n 个点的树,有 m 次查询,每次给两个点 x,y,求 x 是否为 y 的祖先。
dfs 序可以用来表示子树关系,
如果 y 的 dfs 序位置被 x 的 dfs 序区间包含,
则 x 为 y 祖先。
总时间复杂度 \text{O}(n+m)
动态树上问题类
需要掌握:
单点修改+链求和
链修改+单点求值
DFS 序很重要,处理子树时关注 DFS 序
例题
给定一棵 n 个节点的树,有点权,
有 m 次操作,每次会修改 x 点的权值,或者查询 x 所在子树的点权和。
A:
使用 DFS 序的转换,则一个点的子树可以通过 DFS 序转换成一段连续的区间,
问题变为单点修改 + 区间求和,使用树状数组即可解决。
总时间复杂度 \text O(n+m\log n)
给定一棵 n 个节点的树,有点权,
有 m 次操作,每次会修改 x 点的权值,或者查 x 到 y 的路径的点权和。
A:
通过树上差分,将路径和变为查询 x 到根的路径和,
考虑每次修改 x 时影响哪些点到根的路径和,
影响范围为 x 的子树内答案,
则问题转换为单点查询 + 子树加,
使用 DFS 序的方法,变成单点查询 + 区间加
总时间复杂度 \text O(n+m\log n)
给定一棵 n 个节点的树,有点权,
有 m 次操作,每次会把 x 到 y 路径上所有点的权值加上 z,或者查询点 x 的权值。
A:
通过树上差分,将路径和变为查询 x 到根的路径和,
考虑每次修改 x 时影响哪些点到根的路径和,
影响范围为 x 的子树内答案,
于是我们将 x 到根加的时候,实际上将 x 点权进行修改,
查询 x 的值时,实际上查询 x 的子树和,
通过 DFS 序的方法变为单点修改 + 区间求和。
总时间复杂度 \text O(n+m\log n)