初升高数学摸底测试

1. 下列运算正确的是$(\qquad)$ A.$a^2\cdot a^3=a^6$ B.$(ab)^2=a^2b^2$ C.$(a^2)^3=a^5$ D.$a^2+a^2=a^4$ 2. 对于实数$x$，我们规定$\lfloor x\rfloor$表示不大于$x$的最大整数，例如$\lfloor1.2\rfloor=1$，$\lfloor3\rfloor=3$，$\lfloor-2.5\rfloor=-3$。若$\displaystyle\left\lfloor\frac{x+4}{10}\right\rfloor=5$，则$x$的取值可以是$(\qquad)$ A.$40$ B.$45$ C.$51$ D.$56$ 3. $A$、$B$两地相距$160$千米，甲车和乙车的平均速度之比为$4:5$，两车同时从$A$地出发到$B$地，乙车比甲车早到$30$分钟。若求甲车的平均速度，设甲车平均速度为$4x$千米／时，则所列方程是$(\qquad)$ A.$\displaystyle\frac{160}{4x}-\frac{160}{5x}=30$ B.$\displaystyle\frac{160}{4x}-\frac{160}{5x}=\frac12$ C.$\displaystyle\frac{160}{5x}-\frac{160}{4x}=\frac12$ D.$\displaystyle\frac{160}{4x}+\frac{160}{5x}=30$ 4. 已知关于$x$的方程$x^2-(k+2)x+2k+1=0$的俩实数根为$x_1^{}$、$x_2^{}$，若$x_1^2+x_2^2=11$，则实数$k$的值为$(\qquad)$ A.$-3$ B.$3$ C.$±3$ D. 无解 5. 如图所示，$AB$是$\odot O$的切线，$B$为切点，$AC$经过点$O$，与$\odot O$分别相交于点$D$、$C$。若$∠ACB=30\degree$，$AB=\sqrt3$，则阴影部分的面积是$(\qquad)$  A.$\displaystyle\frac{\sqrt3}2$ B.$\displaystyle\fracπ6$ C.$\displaystyle\frac{\sqrt3}2-\fracπ6$ D.$\displaystyle\frac{\sqrt3}3-\fracπ6$ 6. 二次函数$y=ax^2+bx+c$的图像如图所示，反比例函数$\displaystyle y=\frac{ac}x$与正比例函数$y=bx$在同一坐标系内的大致图像是$(\qquad)$  A.  B.  C.  D.  7. 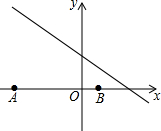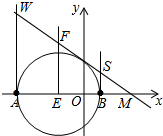如图，已知点$A\;(-8,0)$和点$B\;(2,0)$，点$C$在直线$\displaystyle y=-\frac34x+4$上，则使$\triangle ABC$是直角三角形的点$C$的个数为$(\qquad)$  A.$1$ B.$2$ C.$3$ D.$4$ ## 解析： >  > 如图， > ① 当$∠A$为直角时，过点$A$作垂线与直线交于$W\;(-8,10)$； > ② 当$∠B$为直角时，过点$B$作垂线与直线交于$S\;(2,2.5)$； > ③ 当$∠C$为直角时，则点$C$在以线段$AB$为直径、$AB$中点$E\;(-3,0)$为圆心的圆与直线$\displaystyle y=-\frac34x+4$的交点上。 > 过点$E$作垂线与直线交于$\displaystyle F\left(-3,\frac{25}4\right)$，则$\displaystyle EF=\frac{25}4$。 > $∵$直线$\displaystyle y=-\frac34x+4$与$x$轴的交点$M$为$\displaystyle\left(\frac{16}3,0\right)$， > $∴\displaystyle EM=\frac{25}3$，$\displaystyle EF=\sqrt{\left(\frac{16}3+3\right)^2+\left(0-\frac{25}4\right)^2}=\frac{125}{12}$。 > $∵E$到直线$\displaystyle y=-\frac34x+4$的距离$\displaystyle d=\frac{\displaystyle\frac{25}3×\frac{25}4}{\displaystyle\frac{125}{12}}=5$， > $∴$以线段$AB$为直径、$E\;(-3,0)$为圆心的圆与直线$\displaystyle y=-\frac34x+4$恰好有一个交点， > $∴$直线$\displaystyle y=-\frac34x+4$上有一点$C$满足$∠C=90\degree$。 > 综上所述，使$\triangle ABC$是直角三角形的点$C$的个数为$3$。 8. 如图，$AC=BC$，$∠ACB=90\degree$，点$D$在边$BC$上$($与$B$、$C$不重合$)$，四边形$ADEF$为正方形，过点$F$作$FG\bot AC$，交$CA$的延长线于点$G$，连接$BF$，交$DE$于点$Q$。给出以下结论：①$AC=FG$；②$S_{\triangle BAF}^{}:S_{\text{\tiny矩形}BCGF}^{}=1:2$；③$∠ABC=∠ABF$；④$AD^2=AC\cdot FQ$。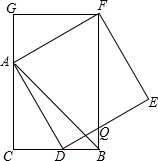其中正确结论的个数是$(\qquad)$  A.$1$ B.$2$ C.$3$ D.$4$ ## 解析： > $∵$四边形$ADEF$为正方形， > $∴∠FAD=90\degree$，$AD=AF=EF$， > $∴∠CAD+∠FAG=90\degree$， > $∵FG\bot CA$， > $∴∠C=90\degree=∠ACB$， > $∴∠CAD=∠AFG$， > 在$\triangle FGA$和$\triangle ACD$中，$\begin{cases}∠G=∠C\\∠AFG=∠CAD\\AF=AD\end{cases}$， > $∴\triangle FGA\cong\triangle ACD\;(AAS)$， > $∴AC=FG$，①正确； > $∵BC=AC$， > $∴FG=BC$， > $∵∠ACB=90\degree$，$FG\bot CA$， > $∴FG\:\!/\!\!/\:\!BC$， > $∴$四边形$CBFG$是矩形， > $∴∠CBF=90\degree$，$\displaystyle S_{\triangle FAB}^{}=\frac12FB\cdot FG=\frac12S_{\text{\tiny四边形}CEFG}^{}$，②正确； > $∵CA=CB$，$∠C=∠CBF=90\degree$， > $∴∠ABC=∠ABF=45\degree$，③正确； > $∵∠FQE=∠DQB=∠ADC$，$∠E=∠C=90\degree$， > $∴\triangle ACD∽\triangle FEQ$， > $∴AC:AD=FE:FQ$， > $∴AD\cdot FE=AD^2=FQ\cdot AC$，④正确。 9. 如图，抛物线$\displaystyle y=-\frac1{12}x^2+\frac23x+\frac53$与$x$轴交于$A$、$B$两点，与$y$轴交于点$C$。若点$P$是线段$AC$上方的抛物线上的一动点，当$\triangle ACP$的面积取得最大值时，点$P$的坐标是$(\qquad)$  A.$(4,3)$ B.$\displaystyle\left(5,\frac{35}{12}\right)$ C.$\displaystyle\left(4,\frac{35}{12}\right)$ D.$(5,3)$ ## 解析： > 连结$PC$、$PO$、$PA$，设点$P$的坐标为$\displaystyle\left(m,-\frac1{12}m^2+\frac23m+\frac53\right)$。 >  > 令$x=0$，则$\displaystyle y=\frac53$，点$C$的坐标为$\displaystyle\left(0,\frac53\right)$， > 令$y=0$，则$\displaystyle-\frac1{12}x^2+\frac23x+\frac53=0$，解得$x_1^{}=-2,\;x_2^{}=10$， > $∴$点$A$的坐标为$(10,0)$，点$B$的坐标为$(-2,0)$，$\displaystyle\begin{aligned}S_{\triangle PCA}^{}&=S_{\triangle PCO}^{}+S_{\triangle POA}^{}-S_{\triangle AOC}^{}\\&=\frac12×\frac53×m+\frac12×10×\left(-\frac1{12}m^2+\frac23m+\frac53\right)-\frac12×\frac53×10\\&=-\frac5{12}(m-5)^2+\frac{125}{12}\;\footnotesize\text{，}\end{aligned}$ > $∴$当$x=5$时，$\triangle PAC$面积的最大值为$\displaystyle\frac{125}{12}$，此时点$P$的坐标为$\displaystyle\left(5,\frac{35}{12}\right)$。 10. 已知直线$y=-\sqrt3x+3$与坐标轴分别交于点$A$、$B$，点$P$在抛物线$\displaystyle y=-\frac13\left(x-\sqrt3\right)^2+4$上，能使$\triangle ABP$为等腰三角形的点$P$的个数为$(\qquad)$ A.$3$ B.$4$ C.$5$ D.$6$ ## 解析： > 以点$B$为圆心、线段$AB$为半径作圆，交抛物线于点$C$、$M$、$N$，连结$AC$、$BC$。 >  > 令$y=-\sqrt3x+3$中的$x=0$，则$y=3$， > $∴$点$A$的坐标为$(0,3)$； > 令$y=-\sqrt3x+3$中的$y=0$，则$x=\sqrt3$， > $∴$点$B$的坐标为$\left(\sqrt3,0\right)$， > $∴AB=2\sqrt3$。 > $∵$抛物线的对称轴为$x=\sqrt3$， > $∴$点$C$的坐标为$\left(2\sqrt3,3\right)$， > $∴AC=2\sqrt3=AB=BC$， > $∴\triangle ABC$是等边三角形。 > 令$\displaystyle y=-\frac13\left(x-\sqrt3\right)^2+4$中的$y=0$，则$\displaystyle-\frac13\left(x-\sqrt3\right)^2+4=0$，解得$x_1^{}=-\sqrt3,\;x_2^{}=3\sqrt3$， > $∴$点$M$的坐标为$\left(-\sqrt3,0\right)$，点$N$的坐标为$\left(3\sqrt3,0\right)$。 > 若$\triangle ABP$是等腰三角形： > ① 当$AB=BP$时，以点$B$为圆心、$AB$为半径作圆，与抛物线交于$C$、$M$、$N$三点； > ② 当$AB=AP$时，以点$A$为圆心、$AB$为半径作圆，与抛物线交于$C$、$M$两点； > ③ 当$AP=BP$时，作线段$AB$的垂直平分线，与抛物线交于$C$、$M$两点； > 综上所述，能使$\triangle ABP$为等腰三角形的点$P$的个数为$3$。