#include <queue>
#include <cstdio>
#include <cstring>
#define rr register
struct point {
int x, y;
point() {}
point(int x_, int y_) : x(x_), y(y_) {}
};
const int MAXN = 50 + 5;
int n, m, t, a[MAXN][MAXN];
const int dx[4] = {1, 0, 0, -1};
const int dy[4] = {0, 1, -1, 0};
bool f[MAXN][MAXN];
void BFS(point st)
{
std::queue <point> q;
q.push(st);
t += (f[st.x][st.y] = true);
int pre = -1;
while (!q.empty())
{
point u = q.front();
q.pop();
for (int i = 0; i < 4; ++i)
{
point v(u.x + dx[i], u.y + dy[i]);
if (v.x < 1 || v.x > n || v.y < 1 || v.y > m) continue; //是否合法
if (a[v.x][v.y] < a[u.x][u.y]) continue; //是否能倒流
if (i + pre == 3) continue; //是否在回退
if (f[v.x][v.y]) continue; //是否已访问
q.push(v);
t += (f[v.x][v.y] = true);
}
}
}
int main()
{
int arr;
scanf("%d", &arr);
for (int cnt = 0; cnt < arr; ++cnt)
{
scanf("%d%d", &n, &m);
memset(a, 0, sizeof(a));
for (rr int i = 1; i <= n; ++i)
{
char c = getchar();
for (; c < 'a' || c > 'z'; c = getchar());
for (rr int j = 1; j <= m; ++j)
{
a[i][j] = c - 'a';
c = getchar();
}
}
memset(f, 0, sizeof(f));
int ans = 0;
for (t = 0; t < n * m; ++ans)
{
int minv = 0x7f7f7f7f;
point minc(0, 0);
for (rr int i = 1; i <= n; ++i)
for (rr int j = 1; j <= m; ++j)
if (!f[i][j] && minv > a[i][j]) {
minv = a[i][j];
minc = point(i, j);
}
BFS(minc);
}
printf("%d\n", ans);
}
return 0;
}
T4 cowtract (网络)
题目地址
题意概括 。有一个 n 条边、m 条边的无向图,每条边有一个权值。现要从中选取若干条边建图,并且要求图 必须连通 ,而且 不能有环 ,求权值和最大的方案。
**分析** 。注意到上面我加粗的八个黑字,懂一点图论常识都会立马想到,“这不就是树吗?” 确实,本题的题意概括起来,其实就是 “最 "大" 生成树” ,那是不是可以直接用 ```Kruskal``` 或者 ```Prim``` 来做呢?真的可以!
本题就是一个最 “小” 生成树的模板,但有一个值得注意的地方 —— 图不能连通的情况要特殊判断。如果你和我一样莽撞,可能就直接想 “它一开始给的边不满 $n-1$ 条边,就肯定无法连通了吧?” 但实际上还有另外一种情况,见下图。
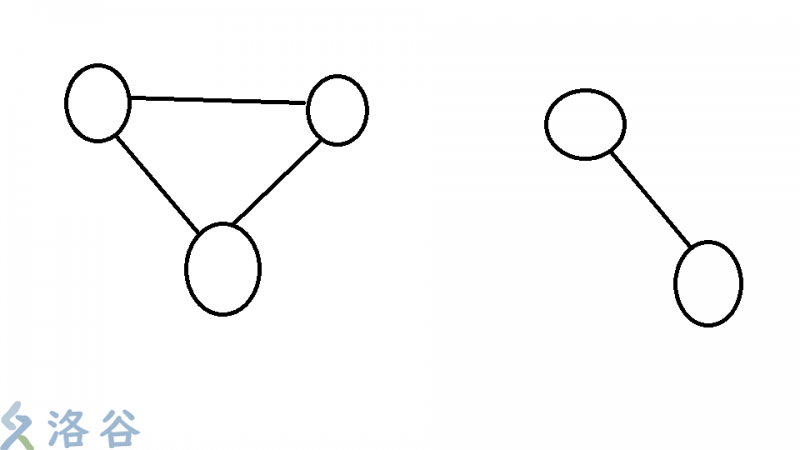
显然,这个图有 $n-1$ 条边,但它无法连通,所以没法直接用初始的边数来判断。
但是,利用最小生成树算法的性质,我们有更轻松的方式来解决这个疑难问题 —— 只看最后算法选出的边数是否等于 $n-1$ 条边即可。显然,当图像上面一样分成几 “块” 时,没法选出 $n-1$ 条边。
**代码** 。下面使用了 ```Kruskal```。
```cpp
#include <cstdio>
#include <cstring>
#include <algorithm>
//Templete
int readint() {
int x = 0;
char c = getchar();
for (; c < '0' || c > '9'; c = getchar());
for (; c >= '0' && c <= '9'; c = getchar()) x = (x << 3) + (x << 1) + (c ^ '0');
return x;
}
void outpint(int x) {
if (x > 9) outpint(x / 10);
putchar(x % 10 + '0');
}
//Global
const int MAXN = 1000 + 5;
const int MAXM = 20000 + 5;
int n, m;
//Graph
int tot;
struct edge {
int from, to, cost;
edge() {}
edge(int _from, int _to, int _cost) {
from = _from;
to = _to;
cost = _cost;
}
} e[MAXM];
bool cmp(edge x, edge y) {
return x.cost > y.cost;
}
//Union Find
int root[MAXN];
int getRoot(int x) {
return root[x] == -1 ? x : root[x] = getRoot(root[x]);
}
int main()
{
n = readint();
m = readint();
for (int i = 1; i <= m; ++i) {
int u = readint();
int v = readint();
int w = readint();
e[i] = edge(u, v, w);
}
std::sort(e + 1, e + m + 1, cmp);
memset(root, -1, sizeof(root));
int ans = 0;
int tot = 0;
for (int i = 1; i <= m; ++i) {
int uRoot = getRoot(e[i].from);
int vRoot = getRoot(e[i].to);
if (uRoot != vRoot) {
root[uRoot] = vRoot;
ans += e[i].cost;
++tot;
}
}
if (tot != n - 1) puts("-1");
else outpint(ans);
return 0;
}
```
# 比赛总结
### 总结题目的推导过程
### 概括今天收获的重点