如何科学的上课传纸条

· · 算法·理论

0. 导论

众所周知，在较为无趣的历史政治音乐美术课上，传纸条都是重要的交流方式。

然鹅，这种方式有一个极大的劣势：容易在传递过程中受到拦截。而且光是拦截了还不要紧，关键是在纸条上传递的信息要是被别人看到泄露了就不好了（x

于是，加密就这样华丽丽地出世了！

1. 太单纯啦！

为了剧情（雾）的连贯性，我们先称这两位同学为 Alice 和 Bob（密码学老常客了

在意识到纸条内容可能被别人（就称之为 Cathy 吧）阅读之后，Alice 同学率先想出了一个绝妙的办法：只要双方的发信息时，都将每个字母向后推一位就可以啦！例如：原句 "I'm fine, thanks, and you?" 就会被转换为 "J'n gjof, uibolt, boe zpv?"。

如果心情好，可以额外再多推几位，只要在消息开头标上推了几位就可以，比如 "7, P't mpul, aohurz, huk fvb?"。

这样，发送的消息在别人眼中都是乱码，只有接收方知道要通过往回移动指定位数获得原本的消息。

于是乎又开始大肆传纸条。

但是，此时的 Alice 和 Bob 都太单纯了，Cathy 作为钻研拦截纸条技术数年的专家，只消看一眼，就知道这就是传说中的“凯撒密码”！名字听着很高大上，然而并没有什么用，仍然轻轻松松被 Cathy 破解了。。。。。。其实方法非常简单，就和 Bob 接收的方法一模一样（

2. 新发现！

在信息又被 Cathy 破译了之后，Bob 痛定思痛，总结了上一次的失败经验。他发现，主要问题是解密用的信息（移动了几位）本身也需要写在明面上传过来，不然连接收方都看不懂了（

于是他下定决心苦苦钻研一种不需要这样做的加密方式，他想了很久。

很久很久很久很久很久很久很久很久很久很久很久很久很久很久很久很久很久很久很久很久很久很久很久很久很久很久很久很久很久很久很久很久很久很久很久很久很久很久很久。

最终，功夫不负有心人，Bob 研发出来一种绝无仅有的新型炒鸡无敌霹雳爆炸人见人爱花见花开车见车爆胎加密大法，加密方式如下：

  1. Alice 和 Bob 每人随机选一个很大的数，称之为 k_a 和 k_b（不要跟化学的那个电离平衡常数搞混了）
  2. Alice 随机再选一个数 P，并且在班里广播：“P=63872357536” （这里 63872357536 代指 Alice 随机选的数）
  3. 接下来，Alice 将 k_a\times P 得到 R_a 并再次在班里广播扰民，Bob 将 k_b\times P 得到 R_b 并且也在班里广播也是扰民。
  4. 那么，现在 Alice 和 Bob 都可以计算出同一个数 C = k_b \times R_a = k_a \times R_b。
  5. 接下来就比较简单啦，比如说还是用上文的向后推字母的方式，但是改成第 i 个字母向后推 C 的第 i 位的值的次数（这样的话每个字母向后推的次数不同， Cathy 也就不知道怎么还原了，但是 Bob 知道 C 的值，所以可以准确还原信息）

在你为这个充满了清澈的愚蠢的加密方式开怀大笑前，我需要先声明一下，Bob 还没有学乘除法（

那么，大家自然就会有一个疑问：Bob 是如何计算这么复杂的乘法的呢？

这就不得不提到 Bob 的（又一个）新发明，他称之曰『快速乘』。

首先，既然他不会乘法，那么把乘法写成 k_a\times P 的形式就是不合理的，正确的写法应该是 \sum\limits_{i=1}^{k_a}P，也就是说，把 P 连加 k_a 次。

那么，考虑这一系列加法：2P=P+P，4P=2P+2P，8P=4P+4P，......P 叠加的效率在不断提高！（加一次相当于加了很多次了）于是乎只要这样算乘法，就能比直接连加 k_a-1 次要快很多了！

当然啦，Bob 只是“觉得”这样算乘法会比较快，但是学过 『时间复杂度分析』之术的你则一定知道，这么计算的时间复杂度是 \Theta(\log k_a)（对于没有接触过时间复杂度这个概念的同学，可以简单认为这个表达的含义是：通过这种方式计算所需要的操作数与 \log k_a 成正比）。读者自证不难，这里留作习题（雾

所以，有了快速乘秘诀的 Bob 自然可以轻松算出 k_b\times P、k_b \times R_a 之类的值了。

但他也知道，如果 Cathy 知道了 k_a 和 k_b 中的任何一个数，这个加密就会无效，毕竟这时 Cathy 也可以算出 C = k_b \times R_a 了。

那么他为什么不担心被破解呢？这是因为虽然乘法有『快速乘』，但是如果不会乘除法却要算“几乘以 P 等于 R_a”的话，就真的得一个一个试了。作为现代人的我们知道，\Theta(\log k_a) 的增长率是远小于 \Theta(k_a) 的，所以 Bob 可以有恃无恐地不断增加 k_a、k_b 的大小，毕竟对自己的计算量没多大影响，却可以把 Cathy 算死。

......

然而 Bob 绝妙的加密方式被一个东西阻挡了。

除法。

3. 现在是我 Alice 的回合！

书接上回，Bob 研究出『新型炒鸡无敌霹雳爆炸人见人爱花见花开车见车爆胎加密大法』后，当天下午他就决定讲给 Alice 听。不料 Alice 曾在课外班提前学过乘除法，没等他讲完就绷不住了。

“有没有一种可能，自然数间有一种东西叫除法？”，Alice 写下一串咒语：

设 X \times P = R_a，X = \sum\limits_{i=0}^{l}x_i\times 10^i，其中 \forall x_i, x_i\in [0,9]\cap\mathbb{N}。

$\therefore$ 每一个 $x_i$ 的值都不受之后数位的干扰，或者说 $0\le R_a-\sum\limits_{j=i+1}^{l}x_j\times 10^j\times P-x_{i}\times 10^{i} \times P\le\sum\limits_{j=0}^{i-1}9\times 10^j\times P$。这就意味着，可以考虑从最高位开始，在每一个 $x_i$ 上依次尝试 $[0,9]\cap\mathbb{N}$ 的值直到满足不等式要求，从而在 $\Theta(l)$ 时间内求出 $X$ 的值。 “现在除法时间复杂度是 $\Theta(\log R_a)$ 了”，Alice 用这句话结束了讲解。 Bob 沉默了。他在深思。~~而且作者要求他在这段时间内赶紧学习一下什么是对数以保证剧情前后 Consistent。~~ 在漫长的思考~~和学习复杂度分析~~后，Bob 再度开口道：“考虑到 $k_a\times P$、$k_a \times R_b$ 的计算使用了快速乘后复杂度都是 $\Theta(\log k_a)$ 的，似乎如果把 $P$ 改的很大就可以阻止 $\Theta(\log R_a)$ 的除法了” Alice 向后靠了靠，轻推一下眼镜，说：“那是因为你计算时间复杂度的时候默认了加法是 $\Theta(1)$ 的操作，假如放任 $R_a$ 增大的话，快速乘的复杂度会随之膨胀至 $\Theta(\log R_a\log k_a)$，使得加密不可行。” Bob 听罢，知道自己的方法已然无效，不由得掩面而泣。 Alice 正要起身，见 Bob 精神状态这么糟糕，安慰道：“但是你的思路还挺有价值的，我想想能不能改造改造。” “真的吗？” ## 4. 其实这时 Alice 真正的回合才到 又是一天晚上，又有一只 Alice 在~~为了某个乱七八糟的承诺~~而在半夜做研究。 除法除法，为什么会有除法呢...... Alice 仔细思考，最终意识到了。之所以可以每一个 $x_i$ 的值都不受之后数位的干扰依次求解，就是因为自然数本身有一个明确的偏序关系，而且当他们同时乘以 $P$ 的时候偏序关系不发生改变，使得 $0\le R_a-\sum\limits_{j=i+1}^{l}x_j\times 10^j\times P-x_{i}\times 10^{i} \times P\le\sum\limits_{j=0}^{i-1}9\times 10^j\times P$ 得到保证。 换句话说，只要让 $P$ 不再是一个越累加越“多”的东西就可以了......最好是个连偏序关系都没有的东西...... 此时，Alice 恰好看向了自己无意在 desmos 中输入的一个椭圆曲线图像。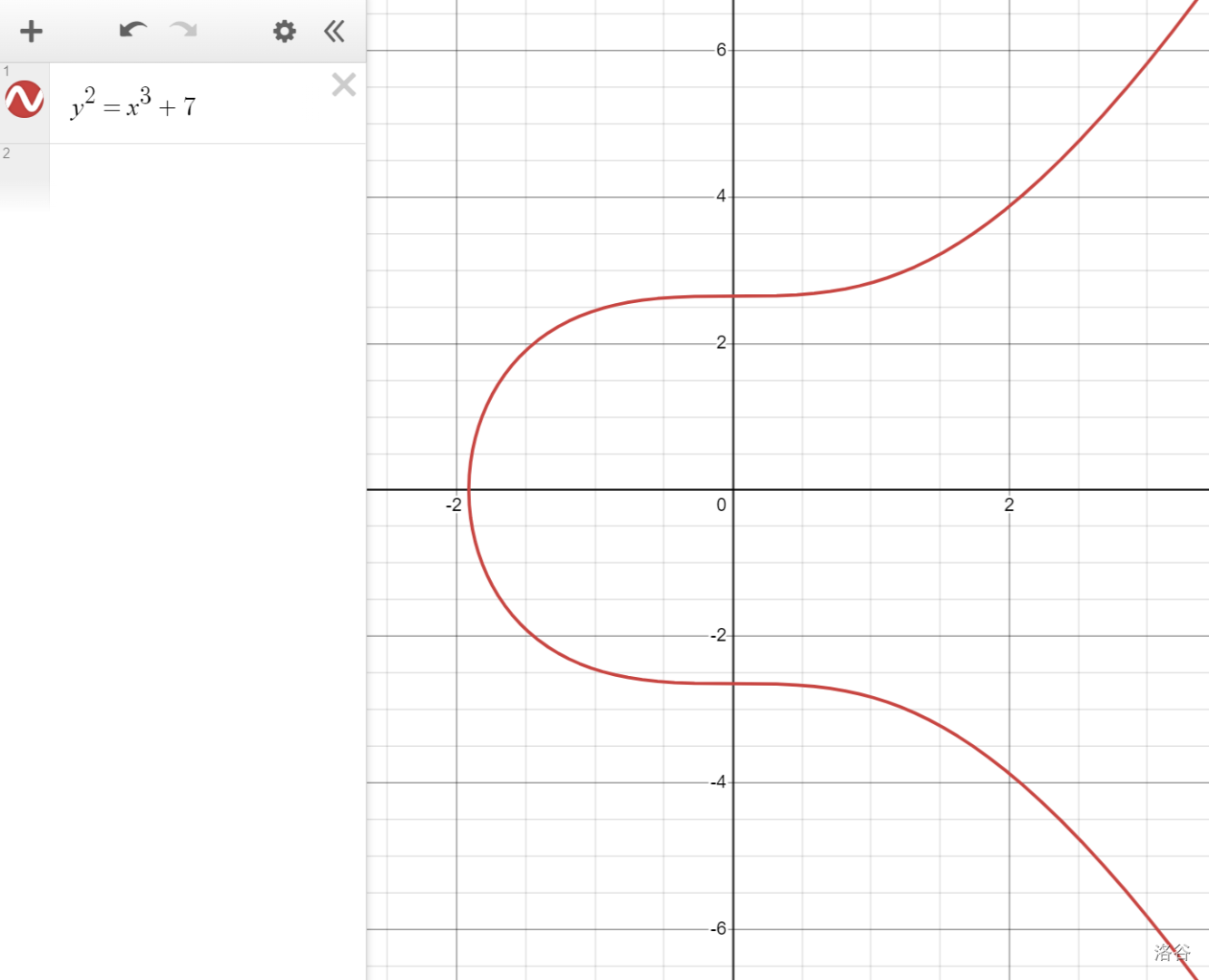 ![](https://cdn.luogu.com.cn/upload/image_hosting/axhmz6o7.png) 对了，直接让 $P$ 是这个图像上的一个点（即 $P\in\{(x,y)\mid y^2=x^3+7\}$）就可以了，毕竟这样肯定是没办法互相比大小了（ 接下来就是要发明出一种新的加法，这样就可以在其基础上扩展出数乘。 一个简单的想法是，对于任意两点 $P$、$Q$，定义其连线（小声：$P=Q$ 的话就用切线）与椭圆曲线的第三个交点 $R:=P+Q$。这样的定义显然满足交换律。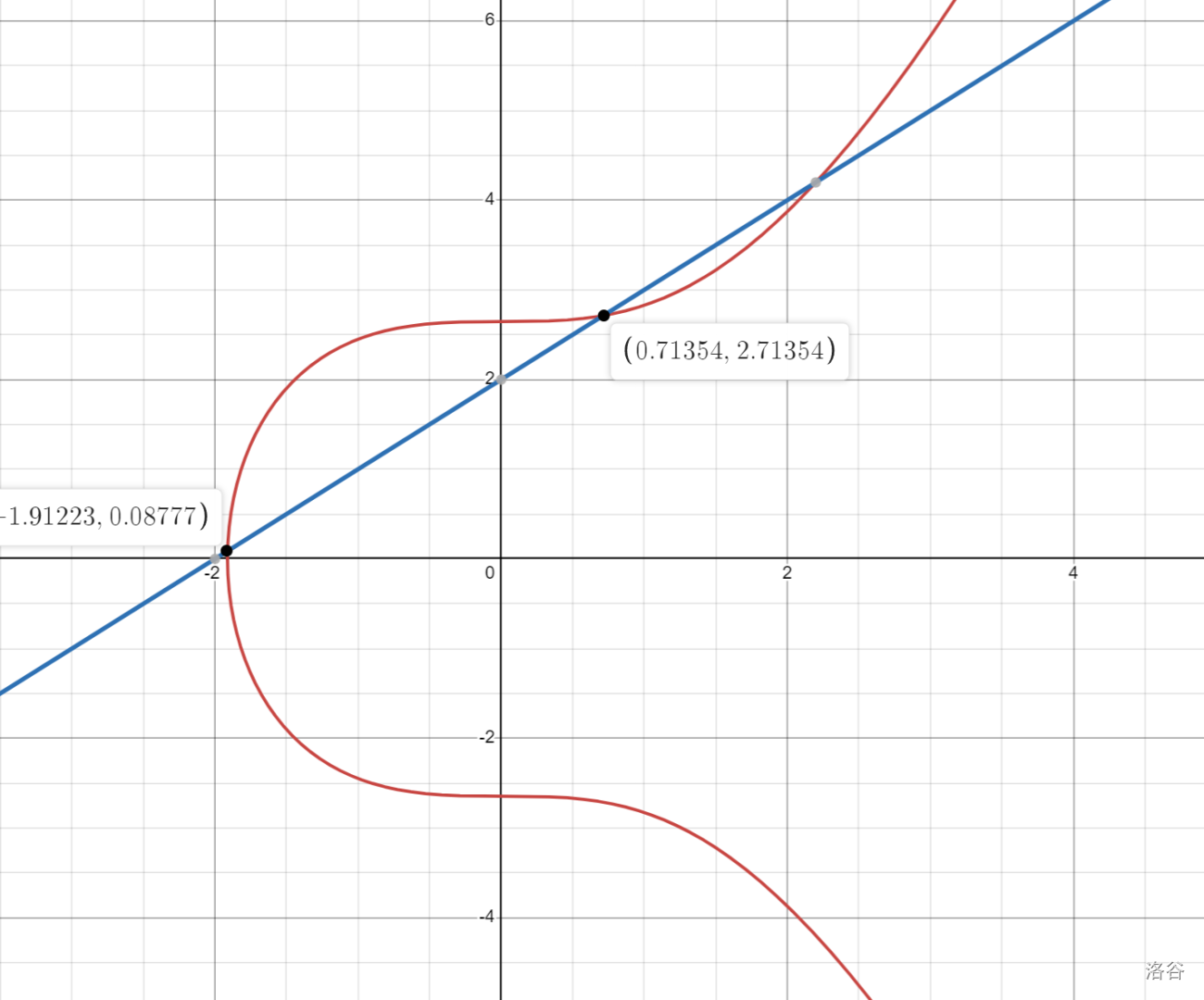 ![](https://cdn.luogu.com.cn/upload/image_hosting/qbbfte61.png) 但这就导致了一个问题：$P+Q=R$ 中 $R$ 的地位与 $P$ 和 $Q$ 不同了，但在图像上$P$、$Q$、$R$ 是轮换对称的，所以有 $P+R=Q$，$R+Q=P$，进而能推出 $P+P+R=R$ 之类的结论，加法直接彻底崩坏了。 为了使 $P$、$Q$、$R$ 在加法的定义式中也是地位平等的，试图改为定义 $P+Q=-R$。 其中，一个点的逆 $-R$ 被定义为这个点关于横轴的对称点，这样可以保证任意的点 $R$ 都有一个确定的逆。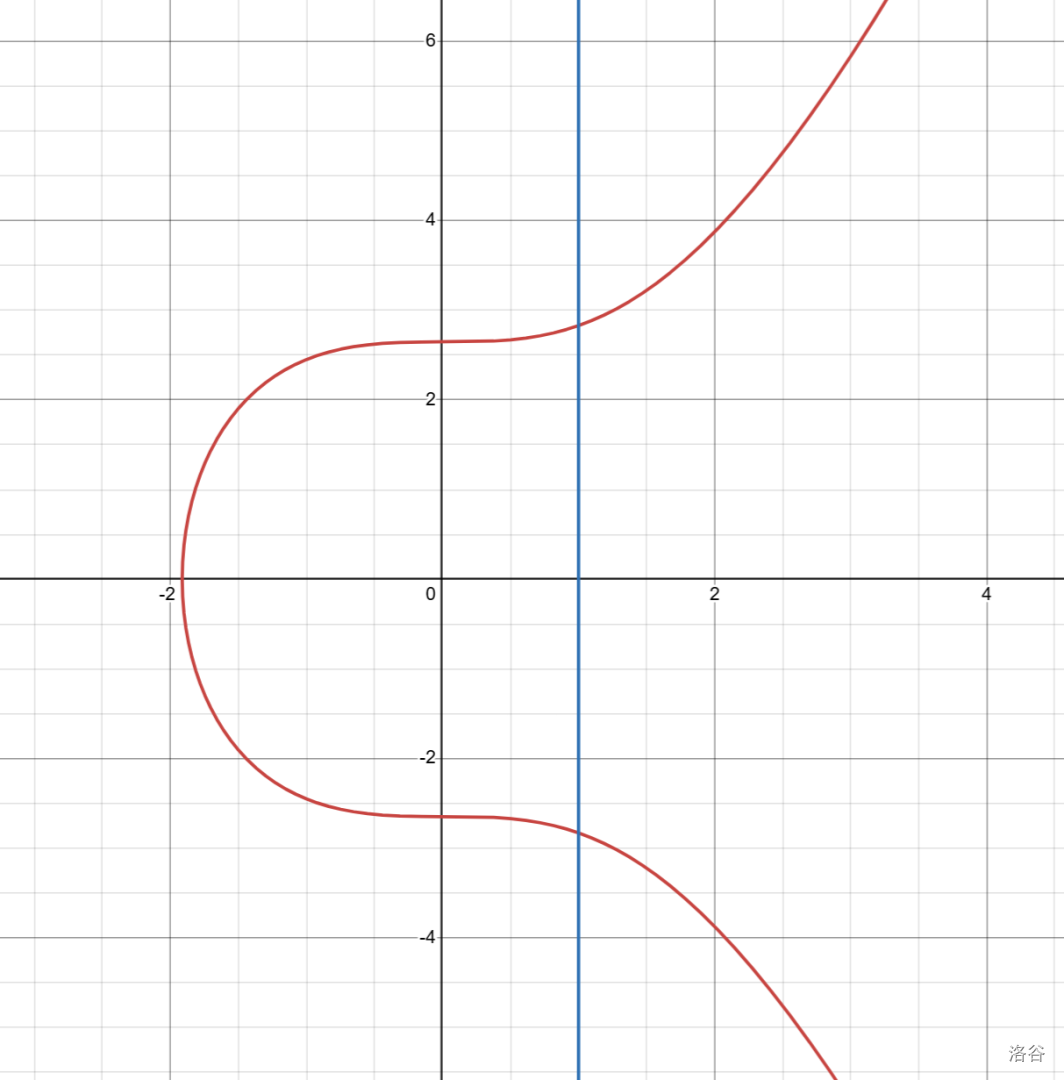 正常来说，$R+(-R)$ 应该等于 $0$，但是不出意外的话又要出意外了（ ![](https://cdn.luogu.com.cn/upload/image_hosting/rensv4xw.png) 这样的直线与椭圆曲线肯定是没有第三个交点的，或者.....干脆定义 $0$ 点为无穷远处，~~众所周知什么都是在无穷远处相交的。~~ 这样就也一起解决了以下这种切线垂直以至于没有第三个交点的情况。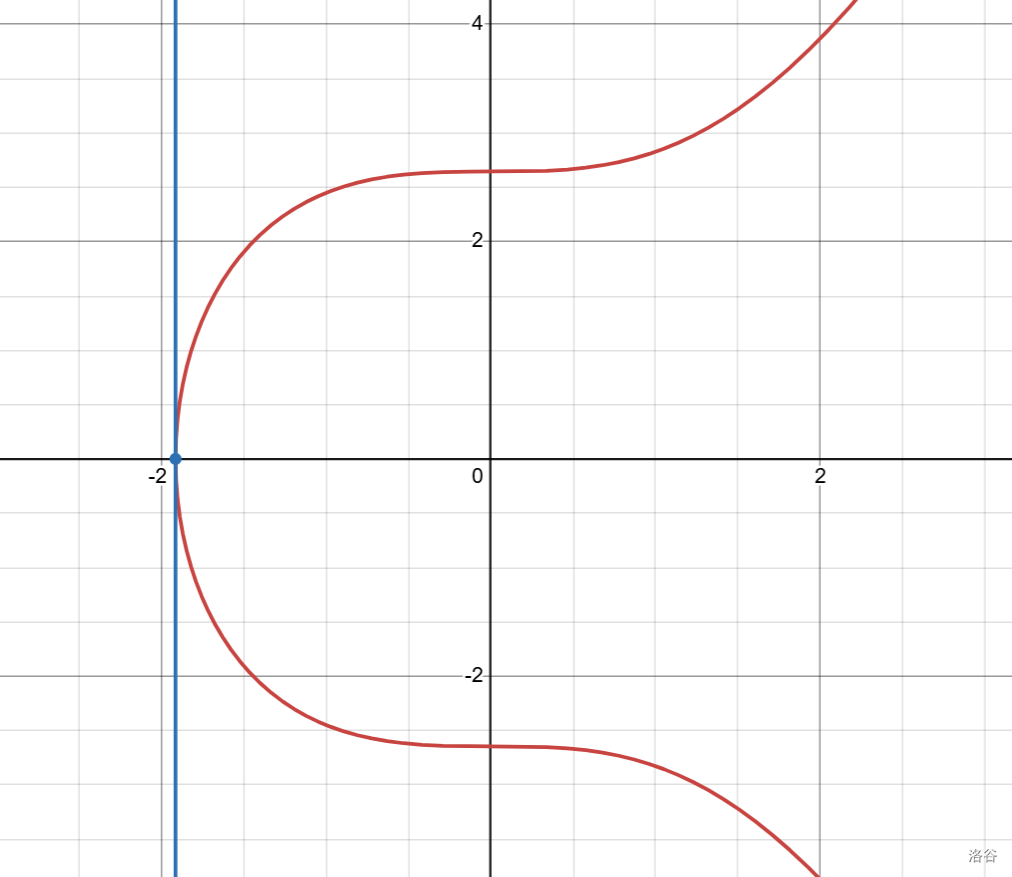 ![](https://cdn.luogu.com.cn/upload/image_hosting/pl9fuuei.png) 此时认为 $P+P=0$。 （聪明的你可能会发现：哎？$Q(0,\sqrt7)$ 处切线不也是只有一个交点吗？但实际上是“第三个交点”与点 $Q$ 重合了，也就是说此时 $Q+Q=-Q$。） 于是乎加法就这样（草率地）定义好了，可是......还需要数乘呢！ Alice 琢磨了一会儿，意识到如果需要数乘，这种加法一定要有『结合律』。不然的话，鬼知道 $P+P+P+P$、$P+P+(P+P)$、$P+(P+P+P)$ 和 $P+(P+P)+P$ 之中谁才是 $4 \times P$ 啊喂！ 为此，Alice 一整夜都在研究椭圆曲线，可惜实在是没什么进展。（至于这里为什么没什么进展，那想必是因为 Alice 没有学过 Cayley-Bacharach 定理）怀着一定不能让 Bob 失望的心情，Alice 在第二天凌晨便下定决心开始暴算，终于通过暴力的代数方法证明了结合律。 ## 5. 终局 每一个作者都是不愿意描写好结局的，所以我就也略过吧，总而言之，Alice 第二天把自己伟大的发明告诉了 Bob，二人欣喜若狂，并创造了以下的加密方式： 1. Alice 和 Bob 每人随机选一个很大的数，称之为 $k_a$ 和 $k_b$。 2. Alice 随机在曲线 $y^2=x^3+7$ 上选一个点 $P$，并且在班里广播 $P$ 的坐标。 3. 接下来，Alice 将 $k_a\times P$（至于乘法怎么算，请看『快速乘』） 得到 $R_a$ 并再次在班里广播坐标，Bob 将 $k_b\times P$ 得到 $R_b$ 并且也在班里广播坐标（~~广播纪元说是~~）。 4. 那么，现在 Alice 和 Bob 都可以计算出同一个点 $C = k_b \times R_a = k_a \times R_b$。 5. 接下来就比较简单啦，比如说还是用上文的向后推字母的方式，但是改成第 $i$ 个字母向后推 $y_C$ 的第 $i$ 位的值的次数（这样的话每个字母向后推的次数不同，Cathy 也就不知道怎么还原了，但是 Bob 知道 $y_C$ 的值，所以可以准确还原信息） 于是，他们过上了幸福的传纸条生活（雾 ## 6. 一些疑惑 读完这个小故事，你可能有一些疑惑。 - Bob 的快速乘到底是怎么做的？ 众所周知每个十进制数都可以被改写成二进制数，设 $k_b$ 的二进制数表示为 $c$，长度为 $l$，$c_i$ 表示 $c$ 的第 $i$ 位，则有 $k_b=\sum\limits_{1}^l{2^{i-1}\times c_i}$，而 $k_b\times P=(\sum\limits_{1}^l{2^{i-1}\times c_i})\times P=\sum\limits_{1}^l{2^{i-1}\times P\times c_i}$。我们可以使用“$2P=P+P$，$4P=2P+2P$，$8P=4P+4P$，......”的方式计算出 $2^1\times P$，$2^2\times P$，$2^3\times P$，......，$2^{l-1}\times P$ 的结果，然后把 $c_i\neq 0$ 那些加起来即可。（而 $l$ 正比于 $\log k_a$） - Alice 的那种邪门加法到底怎么算？（即，给定两点 $P (x_1, y_1)$ 和 $Q (x_2, y_2)$，计算 $P + Q = R (x_3, y_3)$） 这里直接对一般的椭圆曲线方程进行计算：$ y^2 = x^3 + ax + b $。 设连接 $P$ 和 $Q$ 的直线 $l: y = kx + c $。 对于 $P\neq Q$ 的情况： ，$ k = \frac{y_2 - y_1}{x_2 - x_1} $，$ c = y_1 - k x_1 $。 对于 $P=Q$ 的情况： $ y^2 = x^3 + ax + b \Rightarrow \frac{\mathrm{d}}{\mathrm{d}x}(y^2)=\frac{\mathrm{d}}{\mathrm{d}x}(x^3 + ax + b) \Rightarrow 2y\frac{\mathrm{d}y}{\mathrm{d}x}=3x^2+a \Rightarrow k=\frac{\mathrm{d}y}{\mathrm{d}x}=\frac{3x^2+a}{2y} 于是就有： 将直线代入椭圆曲线有 $ (kx + c)^2 = x^3 + ax + b $。 即三次方程：$ x^3 - s^2x^2 + (a - 2sc)x + (b - c^2) = 0 $。 根据性质有 $ x_1 + x_2 + x_3 = s^2 $，即 $ x_3 = s^2 - x_1 - x_2 $。 显然 $ y_3 = -(s x_3 + c )$。 - Alice 为什么证明结合律毫无进展？ 答：因为笔者试图证明也毫无进展。 就实际而言，这个涉及到 Cayley-Bacharach 定理以及一些复杂的说明，推荐阅读：[椭圆曲线加法群结合律的证明 - 爱写文档的工程师](https://zhuanlan.zhihu.com/p/385840962) 和 [【译文】Cayley-Bacharach定理的证明 - 姜很犟](https://zhuanlan.zhihu.com/p/657245459)。 更暴力的方式大概就是利用上述的计算公式暴算。 - Cathy 为什么就没法破解这个新加密方式？ 上次被破解是因为可以用除法反推秘钥，现在！你告诉我！这一个点怎么除一个数啊？！ 总之纸条是安全了。（肉眼可见的开心.jpg）