tricks
1saunoya
2021-09-21 19:22:32
为什么总感觉这玩意好卡,可以保存到本地吧(
感觉缺了点图,可以去博客园里面翻出来?
- FBI Warning:本文不会介绍算法,只会写一些少的可怜的套路。
一些东西还没填。所以暂时不开,如果你恰好猜中了密码,看就看呗。以后会开放的。
upd:打算开放了。大概退役了吧。虽然还是好多没有更新啊。
想到什么写什么。
**如果我补得不全的话只是时间不够。这应该是退役的最后几天写的东西。**
感觉还是很多东西没补上来。
[欢迎来欣赏菜鸡的回忆录](https://www.luogu.com.cn/blog/Isaunoya/momeries-of-OI)
里面可能有很多负面情绪,看着办?
~~如果回忆录忘记开了记得提醒我一下让我打开,1532803101~~
内容杂乱无章,愿意看就看吧,希望对您有用。
如果有啥算法不会,学就完事了,多简单,**你没啥厉害的学长和资源的话更加了**。
这里不想写高等数学内容,但是建议你学高等数学。
随便写一个 $\min\max$ 容斥吧!
$$\large \max(S) = \sum_{T\in S} -1^{|T|-k} \times \binom{k-1}{|T|-1}\min(T)$$
$$\large E(\max(S)) = \sum_{T\in S} -1^{|T| -k}\times \binom{k-1}{|T|-1}E(\min(T))$$
# 简单理论知识
0.不要轻易的开 #define int long long 当然我觉得这个有时候还是有一定用处的,但是不提倡。
1.**合并两颗树的时候,这棵新树的重心一定在两棵树的重心路径之间。合并两颗树的时候,这棵新树的直径一定是原来两条直径的四个端点之二。[LOJ 远行]**
2.看到一个可做的东西,但是是区间的形式,去思考一下**线段树分治**。
3.如果分块的复杂度是 $n \sqrt {n} \log n$ 的话,那么大概率可以调整块长度,让他变成 $n \sqrt {n \log n}$。或者你有时候可以分块套分块,让这个直接去掉一个 $\log$。
4.SAM 空间一定要开 **2|s|+2 以上**。SAM fail 树上的父节点,是它的后缀。记住 SAM 是压缩后的 $trie$。所以两个点的 $lcp$ 是树上的 $dep_{lca}$。
5.看到数据范围小一定要先想状压,数据范围 **long long** 那样的时候一定要打表找规律什么的。
6.很多问题是 $k$ 近,距离和啥的,一定要优先想到点分树/点分治。
7.树状数组是可以区间修改区间查询的,但是功能不及线段树,并不提倡**熟练写线段树的时候去写树状数组**。
7.5 树状数组是可以二分的。
8.线段树上面可以维护很多东西,通常可并,线段树本质是 $2$ 叉树,而分块的本质是 $\sqrt{n}$ 叉树。对此感兴趣可以去查一下 top-tree 虽然很难懂。
9.如果想要 $\sqrt n$ 的树,那么请直接 $prufer$ 序列生成。
补充:
类似伪代码的代码:
```cpp
V<pii> prufer(int n) {
auto A = V(int, n - 2);
for (auto &x : A) {
x = rnd() % n;
}
std::map<int, int> map;
for (auto x : A) {
map[x]++;
}
auto set = std::set<int>();
rp (i, n) {
if (!map[i]) {
set.insert(i);
}
}
auto G = V<pii>();
for (auto i : A) {
int x = i, y = *set.begin();
map[x]--, set.erase(set.begin());
if (!map[x]) {
set.insert(x);
}
G.pb(x, y);
}
G.pb(*set.begin(), *--set.end());
return G;
}
```
10.链下面一个菊花通常是一个有用的数据。如果想要一个奇怪的东西的话直接去找吉老师的构造方法。
11.**高维前缀和搞完的其实是 FWT/FMT 点积。直接相乘就好了。** 能用高维前缀和的千万别用枚举子集。
12.二进制往往可以 meet in middle。感觉 $m = 40$ 啥的就是在暗示了。
13.kdt 的复杂度是 $n ^{2-\frac{1}{k}}$。通常可以排序搞掉一维。
14.题目多挖掘性质,很多时候其实没有你想的那么复杂。
15.习惯用前缀和优化,这样往往可以节省一个 $n$。
16.不要把 $x \times 10$ 写成 $(x << 3) + (x << 1)$ 之类的,浪费时间,没啥用。
**编译器永远的神,比你聪明多了。**
17.多维偏序的情况下,都是可以先排序的。
18.基数排序的复杂度非常优秀,建议广泛学习。
19.不按秩合并的并查集是可以卡到 $n \log n$ 的,当然这个不是我提出来的是别人提出来的,所以这个去看 luogu 的模板题吧。
20.**学会拆柿子和化简,非常重要。**
21.对路径边权有限制的时候,多去想一下 kruskal重构树。
**补充:(kruskal重构树)**
kruskal重构树是用来解决一些诸如“查询从某个点开始 经过边权不超过$val$所能到达的节点”的问题
所以很显然 在最小生成树上是最优的。。其他多余的边可以不需要考虑。。
那我们在跑kruskal的时候重新建边。。
克鲁斯卡尔重构树的思想就是在建最小生成树的时候不是直接连边 而是新建一个节点 并把这个节点的值设为边权 然后令两个连通块的代表点分别作为它的左右儿子 然后令这个新节点成为整个连通块的代表点
即如果$u$ $v$不连通
把$u$ $v$两点连到新建节点上。顺便连边。然后就变成了一棵树。
而这棵树满足一个性质 十分重要 树满足一个最优性…至于图…不放了…自己手动模拟一下就知道了啊…把边权化成点权然后求个[LCA]通常是这个套路吧…
**如果最后的点不是 2n-1 个那么说明这个不是一个连通图,而且你现在构造出来的是一个森林而不是一棵树,多次遍历即可。**
22.**标记永久化,这个绝对会有用的**:[这里](https://www.cnblogs.com/Isaunoya/p/11979419.html)。
23.永远tm不要觉得 $\log^2$ 很牛逼,通常情况打不过 $\sqrt{n}$。$\log^3$ 基本上是一个 $n ^{1-\alpha}$ 了吧。
24.如果一个题覆盖很难做,那么想一下这个点被覆盖了几次即可。https://www.cnblogs.com/Isaunoya/p/12513204.html
25.**无向图边权最大最小的一定在最小生成树上。**
26.网格图通常可以转点网络流。
27.有的题不用网络流,霍尔定理就好了。
**补充:**
Hall 定理:对于一个两边点数相等的二分图,有完美匹配,当且仅当对于左边任意点集 **A**,有 **|N(A)|>|A|** 为与 **A** 中至少一点相邻的点集)。
变式 1:对于一个两边点数均为 **n** 的二分图,最大匹配大小为 $n+\min(|N(A)|-|A|)$。
变式 2:对于一个两边点数均为 **n** 的二分图,左边的一个点集 **A** 能被某个匹配覆盖,当且仅当对于任意 $B\subseteq A$,$|N(B)|\ge|B|$。
1009G。
28.看到一个题很难做就去想 $n \sqrt {n}$ 或者 $n \frac{n}{w}$ ,不一定要 $poly \log$。
29.如果有能力一定要写替罪羊树当平衡树板子。尽量不写树套树,如果要写的话就空间回收的替罪羊树套线段树。
30.无根树在完全图里面有 $n^{n-2}$,有根树就是 $n^{n-1}$个。完全二分图里面有 $n^{m-1} \times m^{n-1}$ 个。(前面两个用 prufer 证明,后面的那个用矩阵树定理暴力消行列式证明。
~~31.STL 是憨批。~~
# 简单套路合集。
## 0
[可持久化介绍在这](https://www.cnblogs.com/Isaunoya/p/11969960.html)
放一点简单数据结构先玩玩?(
https://www.luogu.com.cn/blog/Isaunoya/solution-cf1117g
https://www.luogu.com.cn/blog/Isaunoya/solution-cf1004f
https://www.luogu.com.cn/blog/Isaunoya/solution-cf1055f
https://www.luogu.com.cn/blog/Isaunoya/solution-cf765f
## 深度相关的树形dp
首先去思考长链剖分/线段树合并之类的。
然后整体转移,有人叫这个整体dp?不是很懂(
## 极差
极差是具有可减性的,不要害怕直接拆开算。
比如说 [CF915F](https://www.luogu.com.cn/blog/Isaunoya/solution-cf915f)
看着令人害怕的极差其实转成两个就无所谓啦。
## 反演和其他玩意套起来。
$\sum_{i|n} \mu_i = [n=1]$
$\sum_{i|n} \varphi_i = n$
都是可以证明的自己去找吧。
## 中位数/平均值。
中位数的话其实就是要有一半大于他的一半小于他的,所以我们二分一下把大于他的当做 1, 小于他的当做 -1
然后问题就是找一个 >0 的子串,这个非常 ez 了吧。
平均值的话大概同理,我觉得你听得懂上面的就可以听得懂这个了,就是你把每个数都 -= mid,然后查一下有没有 > 0 的子段,这样就可以了。
大概是 150E 给我的一个启示吧。
[平均值也是原题](https://www.luogu.com.cn/problem/P4292)
而且为啥还是个 WC 题啊。
## DSU ON Tree
暴力的复杂度是对的。
## 线段树合并。
空间尽量开大。但不要 MLE。
考虑下标意义。
## 主席树。
重复利用了很多节点,可以自行对着代码思考一下。
## 值域分块。
对值域分成若干个块 $\sqrt {T}$ 个,其中定义 $T$ 为值域,然后那么这个每个块都是 $\sqrt{T}$,然后就可以直接整了。
我们令 $cnt_{belong_i}$ 为 i 所在的块,我们对 $\forall i, cnt_{belong_i} += 1$,那么这个块就记录了所有信息,我们只需要对这个 cnt 做一个前缀和然后就可以达到我们想要的效果了。
然后我们暴力枚举答案在哪个块里面,然后暴力这个块就好了。复杂度是 $\frac{n}{T} + T$。
对这个其实没什么好说的。另外一提的是,这种做法可以分块套分块,也是去掉 $\log$ 的关键条件。
## 多项式。
多项式有很多东西。不是很想写,也不会太多。
如果不想接触原理就直接背代码。
## 高维前缀和/fmt。
高维前缀和就是 fmt,可以直接拿来卷积。
(其实转化一下就是点积。)
仔细一想你把点积相乘全部加起来其实是会算重复的。
同理高维差分其实就是 ifmt。
求一个点可以用高维容斥。$\sum -1^{popcount(i)+1} (f\times g)_0$。
## 二项式反演。
能顶。
有俩题。
[这里](https://www.luogu.com.cn/problem/P6478)。
[这里](https://www.luogu.com.cn/blog/Isaunoya/solution-p4515)
## 子串相关。
扫描线之类的东西直接子串相关了好吧,就是相邻的一段搞搞。
然后如果说还有什么子串相关的话就是括号树,那个玩意可以算一下最后一个括号带来的贡献然后前缀和,这种玩意都是可以更新的对吧。
# 随机化。
一些玩意可以随机化,比如说状压,数据结构。
https://www.luogu.com.cn/blog/Isaunoya/solution-cf1310d
这里是一个普通题的部分。
还有一个 NB 题。
大致题意:每次操作可以使得序列某个数-1/+1,问最少多少次操作使得全局gcd>1
死也想不到随机化。。
我们考虑到 $\gcd == 2$ 的情况,显然答案的上界是 $n$。
我们考虑答案是不可能超过 $n$ 的,那么至少 $\frac{n}{2}$ 是 0 或 1 。
然后直接随机 $x$ 和 $x - 1$ , $x + 1$ 就可以了。
每次选中的概率是 $\frac{1}{2}$
所以你选 $m$ 个数,那么正确率就是 $1 - \frac{1}{2^m}$。
[可以去找这个博客。](https://www.cnblogs.com/Isaunoya/p/12411474.html)
还有一个留作习题吧,[从某个地方看到的题,挺有意思的](https://www.luogu.com.cn/problem/CF1198F)。
大概做法是随机数列,然后贪心的选,看是否可以。(注意要卡时,如果不行就搞掉)
没想到 F 竟然会放乱搞题。
这是数据结构的部分。
给一个排列,有多少个区间$l,r$是 $l$~$r$ 组成的。
那么问题显然可以用树状数组解决,但是用随机也是一种想法,给每一个数值一个随机值(重新定义)。
然后 $p_i$ 异或一个 $hsh_{p_i}$,$i$ 异或一个 $hsh_{p_i}$。这样当且仅当 $i$ 和 $p_i$ 在一个区间内的时候可以抵消。
如果能相互抵消的那么一定是在一个区间内的。
[某场 edu G](https://codeforces.ml/contest/1418/problem/G)
大概意思是求有多少个区间每个数出现且出现**刚好**三次。
[数据结构的做法。](https://codeforces.ml/contest/1418/submission/92872975)
扫描线,考虑当前扫到 $i$ 有多少个点有贡献(经典做法)
考虑怎么做可以让这个有贡献呢。
令 $k_i$ 是和他相同数值的位置。(意思是 $pre_i$ 是和 $i$ 数值相同的前一个,那么 $k_1 = pre_i$ $k_2 = pre_{pre_i}$)
我们将 $1 ~ i$ 加一。
然后 $k_3 ~ k_2$ 减一。
就变成了有多少个 $0$ 的问题,接下来是简单问题。
这里介绍一个随机化的做法。
考虑这玩意一定要得抵消,那么我们可以自己定义一个 $3$ 进制异或,当这个出现次数是 $3x+k$ 的形式的时候那么这个的贡献是 $1 \times hsh_i$。
如果是 $3x$ 的形式的时候那么这个的贡献是 $-2 \times hsh_i$。
所以是可以抵消的,还是用 $map$ 搞一搞就没啦。
# 数据结构。
## 数据结构拆开算贡献。
[这个题](https://www.luogu.com.cn/problem/CF1167F)
考虑到对所有区间求 $f(l, r)$
$f(l,r) = \sum_{i=1}^{r-l+1}b_i * i$ 然后考虑一下实际意义,i 其实是有多少个数比他小+1(在 [l,r] 区间内)
然后就变得比较可做了。
[还有这个题](https://ac.nowcoder.com/acm/problem/14522)
求所有区间的逆序对数,就考虑一个它会出现在多少个区间内啊
```cpp
__int128 answer = 0;
for (int i = 0; i < N; i++) {
long long left = bit.query(a[i] + 1, N), right = N - i;
answer += left * right;
bit.update(a[i], i + 1);
}
```
大概就是这样?
## 扫描线。
特别注意一点,扫描线通常指的是求面积,或者之类的东西,求周长也用得到?
这个是狭义上的扫描线,实际上的扫描线有更多的用处,比如说 HH 的项链。
HH 的项链其实还不够经典,经典的应该是 NOIOL T2。
我们枚举一个右端点,维护一个数据结构表示从 $r \to r + 1$ 的变化,然后就可以计算全局的贡献。
类似这种贡献 $[\sum_i \sum_j \max(i,j)]$。这个的话用吉司机线段树就可以了,复杂度 $log^2$。
upd:**当时脑抽了,这个可以随便单调栈。**
比较经典也比较好做的是 $\sum_i \sum_j sum(i,j)$ sum(l,r) 表示区间和,那么我们使得当前移到 $r$,之前的状态是 $r-1$,那么我们只需要把 $1$ ~ $r-1$ 全部区间加一个 $a_r$ 就可以了。
返回 NOIOL T2 那题,需要记录一个 lst,表示上一个出现的位置。
扫描线也可以和单调栈一起用,比如说[这题](https://www.luogu.com.cn/blog/0123456-3456789/solution-cf1359d)
链接是 Fzzzz 的题解。
这里有个扫描线的题我还没想出来,等以后填坑的时候看看能不能想到吧。
定义 $g(l,r)$ 是让 $l$~$r$ 联通的最少边数,然后求 $\sum_{1\leq l,r\leq n}g(l,r)$。
upd:**对每条边计算贡献,就可以了。**
## 曼哈顿距离变成切比雪夫距离。/ 切比雪夫距离变成曼哈顿距离。
https://www.luogu.com.cn/problem/P3964
这个题比较好的写了这个东西。
$(x,y)$ 变成 $(\frac{x+y}{2}, \frac{x-y}{2})$ 原坐标系的切比雪夫距离等于曼哈顿距离。
$(x,y)$ 变成 $(x+y, x-y)$ 原坐标系的曼哈顿距离变成切比雪夫距离。
BZOJ数列那题我写过题解,自己去翻一下,就会发现这个可以做。不过这个好像可以通过主席树二进制分组来搞。这里先省略了。
感觉也比较经典?
[BZOJ数列题解](https://www.cnblogs.com/Isaunoya/p/12296012.html)
数列这个玩意还可以二进制分组。(凸包也是可以二进制分组的)
## 二进制分组。
这个可以强制在线。
复杂度可以用 zkw 线段树的结构来证明。
这个套路在 710F 用到过,所以还行。((
二进制分组,其实是下面那个玩意,画的粗略了点。
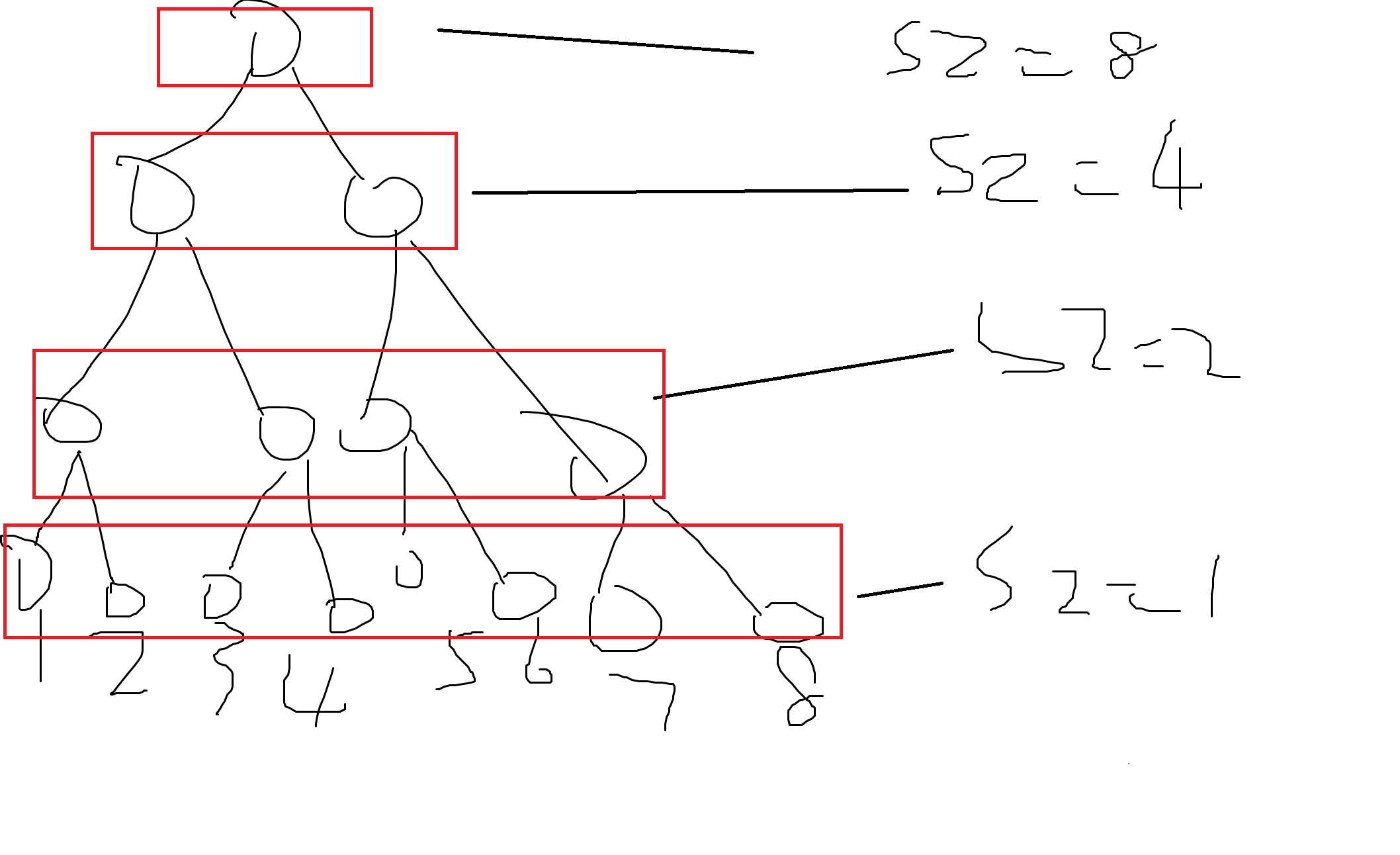
容易证明每个玩意只被合并了 $\log$ 次,因为有 $\log$ 层,所以我们可以这样抽象理解他的复杂度是 $n\ \log\ n$ 的。
然后讲一下这题的做法,我们发现你这样每次合并的复杂度是可控的,也就是你可以把 trie 的信息也这么合并,然后对每个点都建一遍 AC 自动机,这样就能做到在线。
至于查询子串次数,我们只需要查询 fail树 从根到自己的 end 个数就好了。
```cpp
#include <bits/stdc++.h>
using namespace std;
const int maxn = 3e5 + 53;
char s[maxn];
int ch[maxn][26], ed[maxn], fail[maxn], tr[maxn][26], siz[maxn];
int cnt = 1;
struct ACAM {
int rt, sz;
void ins(char* s) {
int p = rt = ++cnt;
sz = 1;
while (*s) {
int c = (*s++) - 'a';
if (!ch[p][c]) ch[p][c] = ++cnt;
p = ch[p][c];
}
ed[p] = 1;
}
void build() {
queue<int> q;
for (int i = 0; i < 26; i++)
if (ch[rt][i]) {
fail[tr[rt][i] = ch[rt][i]] = rt;
q.push(tr[rt][i]);
} else {
tr[rt][i] = rt;
}
while (q.size()) {
int u = q.front();
q.pop();
for (int i = 0; i < 26; i++) {
if (ch[u][i]) {
fail[tr[u][i] = ch[u][i]] = tr[fail[u]][i];
q.push(tr[u][i]);
} else {
tr[u][i] = tr[fail[u]][i];
}
}
siz[u] = ed[u] + siz[fail[u]];
}
}
};
int merge(int x, int y) {
if (!x || !y) return x | y;
ed[x] += ed[y];
for (int i = 0; i < 26; i++) ch[x][i] = merge(ch[x][i], ch[y][i]);
return x;
}
struct ACAutoMaton {
ACAM rt[maxn];
int top;
ACAutoMaton() { top = 0; }
void solve(char* s) {
rt[++top].ins(s);
while (top > 1 && rt[top].sz == rt[top - 1].sz) {
rt[top - 1].rt = merge(rt[top - 1].rt, rt[top].rt);
rt[top - 1].sz += rt[top].sz, top--;
}
rt[top].build();
}
int qry(char* s) {
int ans = 0;
for (int i = 1; i <= top; i++) {
int p = rt[i].rt;
for (char* t = s; *t;) p = tr[p][(*t++) - 'a'], ans += siz[p];
}
return ans;
}
} INS, DEL;
signed main() {
int _;
scanf("%d", &_);
while (_--) {
int op;
scanf("%d", &op), scanf("%s", s);
if (op == 1) {
INS.solve(s);
}
if (op == 2) {
DEL.solve(s);
}
if (op == 3) {
printf("%d\n", INS.qry(s) - DEL.qry(s));
fflush(stdout);
}
}
return 0;
}
```
## 枚举值。
有的区间问题需要枚举一个值,然后计算贡献。略吧。
感觉举不出来例子但是很多的亚子。
噢,就是枚举一个最大值,然后加入最大值到全局,这样就好了。
类似就是这样。
## 阈值/根号分治。
大概是叫做这个的一个东西,这个在数论的方面也可以用得到。
数论方面的应用应该是整除分块,可以用来 $\sum_i \frac{n}{i}$
我们考虑 $\sqrt x \times \sqrt x = x$,那么你的 $x$ 不会超过 $2 \sqrt x$ 个因数,所以我们可以假设枚举因数一样,带上一个前缀和,于是没了。
至于根号分治的话,应该就是一种东西,对 $x \leq \sqrt x$ 和 $x \geq \sqrt x$ 分开搞计算方法。比较常用的办法吧,JSOI原力是个BZOJ权限题,但是能看到题解。
[这里也有一个](https://www.luogu.com.cn/blog/Isaunoya/solution-cf1039d)
应该是一个入门的题了。根号分治也可以跟根号数据结构一起用吧。比如说洛谷就有一个比较经典的题叫哈希冲突。~~(或者说根号数据结构就是根号分治?)~~如果需要其他的根号题,那么可以通过我的博客看吧。其实挺多挺好玩的?根号分治的题要通过玄学调大小吧。(通过值来搞大小也行吧。)
2333
其实还可以去学一下什么 三元环计数,四元环计数,都不是很难。
## 枚举右端点,双指针。
如果需要计算一个贡献,经常需要双指针,这样可以把贡献降到 $O \log -> O 1$
$O 1$ 是均摊的。如果要统计每个数不超过两次的最长区间也可以用这个套路,和数据结构结合的部分应该就可以用这种套路了吧。~~(感觉也是一个扫描线,再见)~~
## 莫比乌斯反演用树状数组维护。
这个在我blog里现在还有两个题(至少写这个的时候是两题)。就是可以和这个弄在一起。先省略掉吧。出的题都还是比较妙的。
## 树套树。
树套树可以用二分来做到 $log^2$,具体做法是把树状数组的 $\log$ 个 $rt$ 搞出来,然后线段树上面二分就做到 $\log^2$ 了。
比较经典吧。好像也没什么可以说的 。
## 二维数点维护连通性。
[IOI狼人](https://www.luogu.com.cn/problem/P4899) & [APIO2019 路灯](https://www.luogu.com.cn/problem/P5445)。
这个随便咋搞吧。
顺便一提路灯可以树套树。
## 块状重构。
[APIO2019 桥梁](https://www.luogu.com.cn/problem/P5443) 。
这个块状重构其实是这样,搞块的时候就可以直接在块里面搞,搞完这个块之后就把修改全部下放。
如果方方方的数据结构不用kd-tree那么就可以块重构了?但是我怎么觉得kd-tree更好写一些啊。
## 树状数组上二分
大概之前做了一个题,用线段树上二分水过去了。其实可以用树状数组二分做的。做法大概是通过一个倒序枚举 $2^x$,添加即可。和倍增差不多?
``自己 yy 出来的东西,对正确性不负责``
upd:原来我口胡出来了树状数组二分啊。。。
噢,所以这位同学你可以去写掉 mex 板子题了。
## cdq 分治。
cdq 分治是一种快速简洁的东西。一般要用树状数组维护,并且用 $sort$ 弄掉一维。我们考虑一个区间 [l,r] ,把 $[l,mid]$ 的贡献加给 $[mid+1,r]$,这个是可以用归并的方式的。
递归即可。
[三维偏序](https://www.luogu.com.cn/problem/P3810)
记得这玩意我学了好久都没学会来着。
放个代码。
```cpp
const int N = 262144;
int n, k;
struct node_t {
int a, b, c;
bool operator ==(const node_t &rhs) const {
return a == rhs.a && b == rhs.b && c == rhs.c;
}
} a[N];
bool cmp(const node_t &x, const node_t &y) {
if (x.a != y.a) {
return x.a < y.a;
} else {
if (x.b != y.b) {
return x.b < y.b;
} else {
return x.c < y.c;
}
}
}
struct point_t {
int a, b, c, cnt, ans;
} b[N];
int len;
struct Binary_Indexed_Tree {
int C[N];
int lowbit(int x) {
return x & -x;
}
void update(int x, int y) {
while (x < N) {
C[x] += y;
x += lowbit(x);
}
}
int query(int x) {
int ans = 0;
while (x) {
ans += C[x];
x ^= lowbit(x);
}
return ans;
}
} f;
point_t v[N];
void solve(int l, int r) {
if (l == r) {
return;
}
int mid = l + r >> 1;
solve(l, mid);
solve(mid + 1, r);
int p = l, tmp = 0;
for (int i = mid + 1; i <= r; i++) {
while (p <= mid && b[p].b <= b[i].b) {
f.update(b[p].c, b[p].cnt);
v[tmp++] = b[p++];
}
b[i].ans += f.query(b[i].c);
v[tmp++] = b[i];
}
for (int i = l; i < p; i++) {
f.update(b[i].c, -b[i].cnt);
}
while (p <= mid) {
v[tmp++] = b[p++];
}
for (int i = l; i <= r; i++) {
b[i] = v[i - l];
}
}
int main() {
rd(n, k);
rep (i, 1, n) {
rd(a[i].a, a[i].b, a[i].c);
}
std::sort(a + 1, a + n + 1, cmp);
int l = 1, r = 1;
while (l <= n) {
while (r <= n && a[l] == a[r + 1]) {
++r;
}
b[++len] = (point_t){a[l].a, a[l].b, a[l].c, r - l + 1, 0};
l = r + 1;
}
solve(1, len);
static int ans[N];
rep (i, 1, n) {
ans[b[i].ans + b[i].cnt - 1] += b[i].cnt;
}
rp (i, n) {
pt(ans[i], "\n");
}
return 0;
}
```
cdq 分治还有一种妙用,可以用来优化 $dp$,先搞左区间然后右区间。树状数组不用清空,查询即可。大概 某个省选题叫做 序列 可以拿来用。
[题目链接在这](https://www.luogu.com.cn/problem/P4093) 。
## 平衡树。
splay 不咋会,只会背一个 lct 的 splay 板子。
## fhq treap
众所周知 Fhq Treap 是 fhq 神仙研究出来的平衡树…
具体实现
每个点实现一个 $\text{rnd}$ 表示 rand 的值 为什么要 rand 呢
是为了保证树高为 $\log n$ 从而保证复杂度…
FHQ Treap的核心操作是split和merge,其他的操作均以这两个操作为基础进行。
下面所述操作的数据如下所示:
```cpp
int rt = 0 , cnt = 0 , a[N] , sz[N] , rnd[N] , ch[N][2] ;
#define ls(x) ch[x][0]
#define rs(x) ch[x][1]
```
ls 指的是左儿子 rs 指的是右儿子…
val表示节点的权值 用来维护二叉搜索树的性质,rnk表示节点的权值 用来维护堆的性质。
sz 表示节点大小(包括自身)
> split
split 实现的操作大概是 把一棵树分成俩…然后左边的值小于等于 $k$ 右边的值大于 $k$
如果你 `split(rt , k , x , y)`
那么你就把 rt 分成两个部分 $x$ ,$y$ 了 其中 $x$ 的子树的 $val \leq k$ , $y$ 的子树的 $val > k$
```cpp
void split (int cur , int k , int & u , int & v) {
if(! cur) { u = v = 0 ; return ; }
if(a[cur] <= k) { u = cur ; split(rs(u) , k , rs(u) , v) ; }
else { v = cur ; split(ls(v) , k , u , ls(v)) ; }
pushup(cur) ;
}
```
代码如上 如果小于这个则分给左子树 大于就分给右边……
> merge
merge的操作就是合并一下根节点和新建节点 然后保留根/替换根(rnd决定)
反正是随机合并 期望树高 $\log n$
```cpp
int merge (int u , int v) {
if(! u || ! v) return u | v ;
if(rnd[u] < rnd[v]) { rs(u) = merge(rs(u) , v) ; pushup(u) ; return u ; }
else { ls(v) = merge(u , ls(v)) ; pushup(v) ; return v ; }
}
```
> kth
Treap 都满足一个堆的性质… 所以显然…
可以按照 sz 来找 kth 递归/非递归都可以啊…
```CPP
int kth(int u , int k) {
if(k <= sz[ls(u)]) return kth(ls(u) , k) ;
if(sz[ls(u)] + 1 == k) return a[u] ;
return kth(rs(u) , k - sz[ls(u)] - 1) ;
}
```
递归写法
> rank
rank的话就分离一个 $val = k-1$ 的子树…然后求这个子树的 sz 就知道 rank 了啊
```cpp
int rank(int k) {
int x , y , res ; split(rt , k - 1 , x , y) ;
res = sz[x] + 1 ; rt = merge(x , y) ; return res ;
}
```
其他操作不讲了
## 替罪羊树
替罪羊树的 $\alpha = 0.75$ 的时候跑的飞快,当然要具体情况调。
然后暴力重构是对的。复杂度是 $n \log n$
## KDT。
KDT 好像就一个板子,还有一个 NOI2019 考了个 KDT 优化建图?。
好像有个奇怪的东西,可以用 KDT 查 k 远点啥的,不知道复杂度假不假。到时候填一下吧。~~(update:临近点都是假的.jpg)~~
这是一篇又长又烂的学习笔记,请做好及时退出的准备。
KD-Tree 的复杂度大概是 $O(n^{1-\frac{1}{k}})$
$k$ 是维度
由于网上找不到靠谱的证明,咕了。
会证明之后再补上。
前置?
- 考虑到平衡树不能做多维,kdt就是扩展到多维情况
- 每次 $nth\_element$ 的复杂度是 $O(n)$ 的。
- 类似替罪羊的想法,如果树不够平衡,直接 pia 重构
- 考虑你删除元素不方便,据说只能打上标记啥的)
- 但是你插入元素不改变树的大致结构 qwqwq
建树显然是 $n \log n$ 的
插入据说是 $n \log^2 n$ 的
查询依旧是 $n \log n$ 的 qwq
- 考虑建树

假设最开始有这么多个点

选一个中位数,把空间一分为二
左边作为左儿子,右边作为右儿子
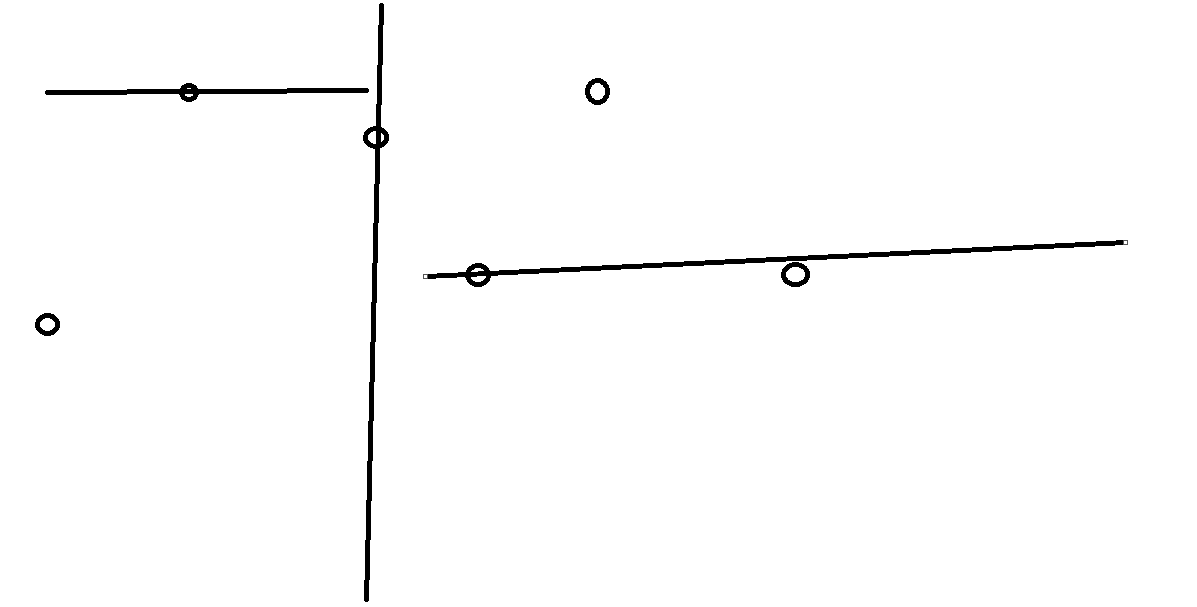
再取一次
我们定义初始是这样
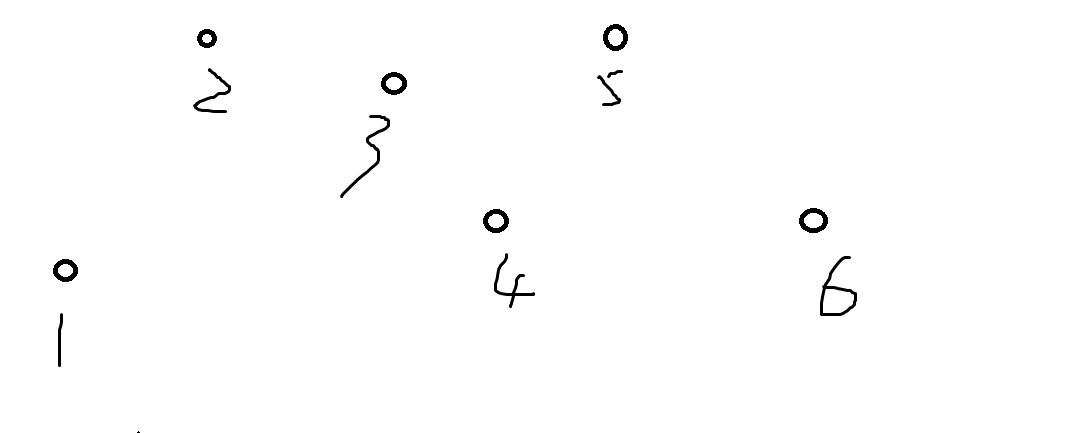
类似平衡树的结构
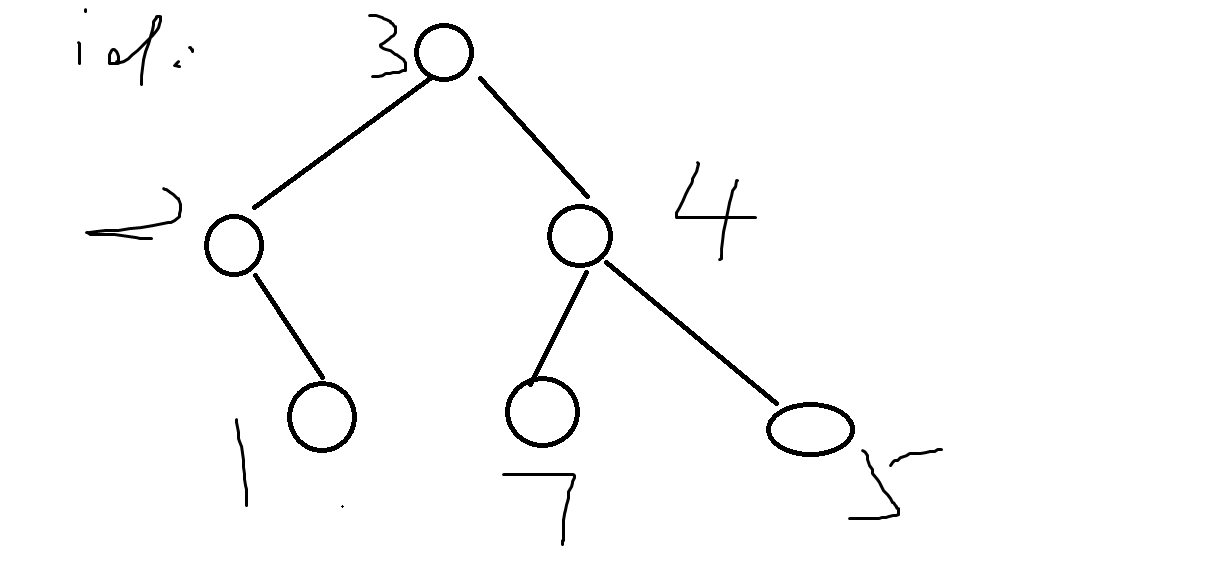
建出来的树长成这样子
然后像平衡树一样维护最小横坐标,纵坐标,最大横坐标,纵坐标,当前权值,当前坐标,sum值,就可以了。
代码亦不难
```cpp
int build(int l , int r , int p) {
now = p ;
int mid = l + r >> 1 ;
nth_element(data + l , data + mid , data + r + 1) ; // data 是原数组 qwq 是 KDT
qwq[mid] = data[mid] ;
if(l < mid) qwq[mid].ls = build(l , mid - 1 , p ^ 1) ;
if(r > mid) qwq[mid].rs = build(mid + 1 , r , p ^ 1) ;
pushup(mid) ; return mid ;
}
```
- 考虑修改
插入时要判是否平衡,如果不平衡就擦除一整棵子树并重构。(类似替罪羊树的想法
```cpp
void Erase(int x) {
if (!x) return;
pp[++m] = P[x], Erase(ls(x)), Erase(rs(x)), erase(x);
}
inline void insert(Point p) {
int top = -1, x = root;
if (!x) {
pp[1] = p, root = build(1, 1, 1);
return;
}
while (233) {
if (max(sz[ls(x)], sz[rs(x)]) > sz[x] * alpha && top == -1) top = x;
++sz[x], cmin(L[x][0], p.x), cmax(R[x][0], p.x), cmin(L[x][1], p.y), cmax(R[x][1], p.y);
int& y = ch[x][(tp[x] == 0) ? (!cmpx(p, P[x])) : (!cmpy(p, P[x]))];
if (!y) {
y = NewNode();
L[y][0] = R[y][0] = p.x, L[y][1] = R[y][1] = p.y, sz[y] = 1, tp[y] = tp[x] ^ 1, fa[y] = x, P[y] = p;
break;
}
x = y;
}
if (top == -1) return;
m = 0;
if (top == root) {
Erase(top), root = build(1, m, 1);
return;
}
int f = fa[top], &t = ch[f][(tp[f] == 0) ? (!cmpx(P[top], P[f])) : (!cmpy(P[top], P[f]))];
Erase(top), t = build(1, m, tp[f]);
}
```
这样就可以了
询问其实因题目而定的。。没什么具体做法
```cpp
int query(int x, int l0, int r0, int l1, int r1) {
if (!x) return 0;
if (l0 <= L[x][0] && R[x][0] <= r0 && l1 <= L[x][1] && R[x][1] <= r1) return sz[x];
if (r0 < L[x][0] || R[x][0] < l0 || r1 < L[x][1] || R[x][1] < l1) return 0;
return query(ls(x), l0, r0, l1, r1) + query(rs(x), l0, r0, l1, r1) +
(l0 <= P[x].x && P[x].x <= r0 && l1 <= P[x].y && P[x].y <= r1);
}
```
比如这个就是二维数点查询个数的方法
顺便一提 k短路 据说有除了 * 的做法。
## 可撤销并查集。
就是那种通过奇怪的合并方式,保证复杂度的并查集,但是不能路径压缩,不然就不可撤销了。
复杂度是 $\log n$ 。
## 线段树分治。
线段树由于奇奇怪怪的性质,反正只会分成 $\log$ 个区间,添加操作以及之类的。这个要记得正难则反,而且要离线。
~~前面写了一个可撤销并查集,是因为这里要用到。~~
很多题,blog里找。
注意到一点:**有一些线段树分治是假在线,所以看到在线的时候是不用怕的。**
[比如说这题嗷](https://www.luogu.com.cn/blog/Isaunoya/solution-cf1217f)
[这里还有一点题](https://www.cnblogs.com/Isaunoya/category/1616734.html)
## 线段树合并。/01trie合并。/启发式合并。
应该归类到启发式合并吧。这个不是特别好说。启发式合并和这个有点点区别。
启发式合并,每次选择 $u$ $v$ 合并信息到一起,把小的合并到大的。这个就可以做到变成自身大小的最小两倍了。复杂度易证 $n \log n$。
线段树合并和01trie的本质合并是一样的。单次复杂度 $u \cap v$,为了方便表示,用放缩法,这个玩意 $u \cap v \leq \min(u,v)$ $f(u+v) = f(u) + f(v) + \min(u,v)$。
入门题应该是晋升者计数。还行。
这样就做完了。然后线段树合并上可以放线段树的标记。~~就很离谱。~~
详见 PKUWC2018 Minimax 我的题解。现在好像又多了一个线段树合并题,NOI2020 D1T2。
## 三叉01trie
AGC044C,到时候填坑。
upd:还不会,鸽了。
## trie 搞MST。
[这题吧](https://www.luogu.com.cn/problem/CF888G)
考虑要使得每个点联通,那么需要每个部分都要联通,首先发现重复的权值都是白给。
然后考虑跨越子树联通即可。
```cpp
function <long long(vector <int>, int)> solve = [&](vector <int> qwq, int fk) {
if(!qwq.size() || fk == -1) return 0ll;
vector <int> son[2];
for(int x: qwq)
son[(x >> fk) & 1].pb(x);
int res = 0, rt = 0;
if(son[0].size() && son[1].size()) {
res = 1ll << (fk + 1);
rt = cnt = 0;
for(int x: son[0]) ins(rt, x, 30);
for(int x: son[1]) res = min(res, qry(rt, x, 30));
}
return solve(son[0], fk - 1) + solve(son[1], fk - 1) + res;
};
```
## trie 整体+1
这个套路大概是联合省选2020 D2T2教会我的。
感兴趣就去做嘛(
## 分块。/莫队。
分块的话其实有很多套路,可以用 bitset 可以用倍增,这个玩意我在 雅礼集训 里面提及过。有兴趣自己看看?
噢,这里有个 [bitset 分块](https://www.luogu.com.cn/blog/Isaunoya/solution-cf1093e)
有些题比如说 Ynoi2019 模拟赛III 的那题,可以用 vector 维护相同权值的位置。雅礼集训还有一个题是比较好的,就是[爷](https://www.cnblogs.com/Isaunoya/p/12398465.html)这个题。
好像这里雅礼集训还有个分块&bitset [这里](https://www.cnblogs.com/Isaunoya/p/12309470.html)
分块的话可以做小 Z 的袜子。这个理解一下就可以了叭?
树分块的话是在树上选点。然后暴力,例题 COT2 强制在线。
莫队好多玩意。感觉乱写会被 d,我博客里应该写了一些``入门的莫队``吧。记住回滚这个办法就行了。二次离线大概是个前缀和,觉得以后也不怎么用得到?~~(其实是我块忘了。)~~
树上莫队啥的也行呗。树上莫队要考虑 $lca$。例题 COT2(SPOJ **非强制在线**)
带修莫队大概就是暴力,复杂度 **最优** 是 $n^{\frac{5}{3}}$。例题 940F。
~~update:HNOI2016 大数 在考试的时候没做出来,耻辱。~~
**回滚莫队**简单介绍。
**按左端点所在的块排序 如果相同 按右端点排序 然后对于每个块求解。弄个右指针在块的最右边。 分类讨论一下 如果左右指针共处一个块内 直接暴力 就是根号级别的 如果不在一个块内 由于右端点是递增的 考虑移动右端点 左边的贡献直接从 q[i].l ~ 块的最右边 暴力就行了**
这边有一个回滚莫队,感觉就是因为普通莫队维护顺序太难了,所以才有这玩意。
区间逆序对,当时 NOI2020 的 T3,写着写着调不出来普通的莫队,然后莽了一个回滚莫队调了半天,这个确实比普通莫队复杂度容易证明而且可以撤销,就很棒,但是记得 $long long$ 问题,不能和 NOI2020 一样挂掉一堆分数((
## 主席树。
主席树就是一个完完全全的前缀和,可以用树上的前缀和来搞,$upd(x,fa[x],this)$ 就行了。
好像也没啥,TTM可以做一下?就标记永久化(
## 势能分析。
~~不会。~~
好像写了好几个势能分析的题了。就是那种 $mod$,$div$ 之类的,固定次数的,暴力那种。((
如果需要例子的话,那么雅礼集训的第一题是一个非常好的例子。
雅礼集训第一题的题解我还没写诶,草了(
于是它 鸽 了。
这个还有好多势能分析,比如说
[1](https://www.cnblogs.com/Isaunoya/p/12595575.html)
[2](https://www.cnblogs.com/Isaunoya/p/13502760.html)
## 维护直径。
维护直径有两种办法,第一种是启发式合并,第二种是LCT。
假设 $u$ 的直径是 $p1,p2$
假设 $v$ 的直径是 $p3,p4$
那么$merge(u,v)$之后的直径一定在这4个点的6种组合的其中一种。
这个是远行告诉我的,后来也做了 Claris 的某一场比赛,里面线段树分治搞了搞。这个大概是暑假的一场比赛吧,如果是校内的人的话建议去做做 Claris 的几套题,挺好的,虽然难度有点低就是了。
## 动态dp。
做了一个简单的动态dp,其实就是维护矩阵啦。[这里](https://www.luogu.com.cn/blog/Isaunoya/solution-cf1380f)
~~全局平衡二叉树,略。~~
LCT每个节点维护一个矩阵,access切换实边搞一下,好像很多题都是这样在access上操作的。不过背板子就好啦。
## 李超线段树。
比较基础的线段树之一吧?
- 如果两端都是大于的或者都是小于的那么显然。
- 斜率大的保留,斜率小的更新下去。
```cpp
struct Line {
int k, b; inline int val(int x) { return k * x + b; }
} s[maxn];
void ins(int &p, int l, int r, int num) {
if(!p) { p = ++cnt; id[p] = num; return; }
int mid = l + r >> 1, &x = num, &y = id[p];
int midx = s[x].val(mid), midy = s[y].val(mid);
if(midx < midy) { x ^= y ^= x ^= y; }
int lx = s[x].val(l), ly = s[y].val(l);
int rx = s[x].val(r), ry = s[y].val(r);
if(lx >= ly && rx >= ry) return;
if(lx < ly) ins(ls[p], l, mid, num);
else ins(rs[p], mid + 1, r, num);
}
```
~~这个是 CF932F 的代码段~~
动态开点的李超树。
感觉李超树和点分树这个组合很经典啊?碰到过两次了。
https://www.luogu.com.cn/blog/Isaunoya/solution-cf1303g
这里是其中一次还有一次是在校内 OJ 上。
## zkw线段树。
Judge 大爷的 blog 好像有一个挺详细的。不过我平时都不写 zkw 线段树的。
这个可以去 www.cnblogs.com/Judge 里面看,应该是高赞博文吧。
好像就写过一次,挺方便的。也挺好理解的。
~~ps:这个 zkw 线段树只能从下到上更新,这个被用功能换来的常数,所以不建议使用,单点更新的时候还是可以用的。~~
```cpp
struct zkw_segment_tree {
int l, s[maxd << 1];
zkw_segment_tree() { l = 1; }
void build() {
while(l < nd) l <<= 1; --l;
for(int i = 1 ; i <= nd ; i ++) s[i + l] = i;
}
void upd(int x) {
x += l; x >>= 1;
while(x) {
s[x] = dis[s[x << 1]] < dis[s[x << 1 | 1]] ? s[x << 1] : s[x << 1 | 1];
x >>= 1;
}
}
void del(int x) { s[x + l] = 0; upd(x); }
} zkw;
```
## 整体二分。
讲过,这里再详细点展开吧。
整体二分大概就是这么一种算法
- 基本上和树状数组一起用
- 离线
- 二分
好进入正文
这题给出多个询问 而你每次询问的复杂度是 $O(n \log n)$ 看似很优秀了?
但你这样的话 所有的复杂度都是 $O(n \log n)$ 整体复杂度乘个 $Q$ 接受不了…
二分怎么写?
```cpp
while(l <= r) {
int mid = l + r >> 1 ;
if(chk(mid)) { ans = mid ; l = mid + 1 ; }
else r = mid - 1 ;
}
```
大概是这样 反过来的不说了…
然后每次边做 边丢队列里…
存俩队列 q1 , q2
满足 条件的放 q2 减掉左区间的贡献
不满足的放 q1 不做修改
易证明 q1.size + q2.size = q.size
然后抵消贡献 这个贡献有时候可以用-1 +1 来处理掉(即存两个)
所以归位 然后接着分治 如果说 L==R 了 就和二分一个样子 赋上 ans = L 跑路如果二分的话,单个询问非常显然,我们现在搞得是 $[l,r]$。然后根据 $check mid$ 来移动 $l,r$。
整体二分的话就是推广了一下这个做法,对于每个 $[l,r]$ 放了个队列,然后一边二分,一边往新队列丢东西,最后一层的时候就得到答案。
整体二分可以用一些奇怪的姿势,维护连通性,见 [WD 的地图](https://www.luogu.com.cn/problem/P5163)。
# 动态规划。
## 数位dp
~~我好像还有一个恨七不成妻没做~~
大概就是记忆化搜索。
啊不会不会不瞎扯了。
## 区间dp
好像我博客里面有好几个区间dp的好题,THUWC的那就是。
啊我也不会不瞎扯了。
## SOSdp
就是超集dp吧。比如说[1234F](https://www.luogu.com.cn/problem/CF1234F)。
超集dp的过程大概就是枚举每一位。
```cpp
for (int i = 0; i < (1 << 20); ++ i) {
if (can[i]) mx[i] = max(mx[i], __builtin_popcount(i));
for (int j = 0; j < 20; ++ j) if (!(i >> j & 1)) {
mx[i | 1 << j] = max(mx[i | 1 << j], mx[i]);
}
}
```
考虑令 $f_x = \max_{u\&x==u} a_u$。任意两个能拼接起来,于是
```cpp
for (int i = 0; i < (1 << 20); ++ i) {
if (can[i]) ans = max(ans, __builtin_popcount(i) + mx[((1 << 20) - 1) ^ i]);
}
```
即可。
超集dp其实还有挺多题的?只是我没找到吧?
又做了一个题。
[CF449D](https://www.luogu.com.cn/problem/CF449D)
考虑高维前缀和?(好像有人叫这个 SOSdp?)
类似状压的过程。
我们可以求出来 $f_i = \sum_{i \& j == i} a_j$
这种就是高维前缀和了。当然可以扩展到 $\max$ 和 $\min$。
这些是可并的。
我们先开个桶计数,令这个桶为 $a_i$,表示 $i$ 出现了几次(
然后就是高维前缀和的操作了。
$f_i = \sum_{i \& j == i} a_j$
通过枚举位,然后加进去贡献。
```cpp
for (int i = 0; i < 20; i++) {
for (int j = 1048575; ~j; --j) {
if (!(j & (1 << i))) { f[j] = add(f[j], f[j ^ (1 << i)]); }
}
}
```
然后我们处理出的 $f_i$ 的意义就是 $j \& i == i$ 的个数。
令 $g_i = 2^{f_i}-1$ 也就是 $\texttt{and}$ 和为 $j$,且 $j \& i == i$ 的方案数。
我们设 $h_i$ 为 $\texttt{and}$ 和为 $i$ 的方案数。
那么 $g_i = \sum_{i\&j==i} h_j$ (显然)
于是我们把前缀和变成差分就好了。
这里还有几个题,这里总结一下。
初始所有 $a_i=0$。
$q$ 次操作。
每次操作形如:
$1$ $x$ 表示把 $a_x=a_x+1$。
$2$ $x$ 表示需要你求出 $\sum_{i\&x==i}a_i$。
这里的 $\&$ 是位运算。
> OI-Wiki 上的解释:
| 运算符 | 解释 |
| ------ | --------------------------------- |
| `&` | 只有两个对应位都为 1 时才为 1 |
| `|` | 只要两个对应位中有一个 1 时就为 1 |
| `^` | 只有两个对应位不同时才为 1 |
对于 $30\%$ 的数据,$\max\{x\}\leq 2^{8}$。
对于 $100\%$ 的数据,$ q \leq 100000,\max\{x\} \leq 2^{16}$。
时限 $1s$,空间 $128M$。
这个可以做到 $q \sqrt n$。
因为这个是可以通过根号均衡复杂度来的。
这个其实不算高维前缀和,但是算一个 $trick$。
[HDUOJ 5977 Garden of Eden]()
这个玩意比较简单了,直接点分治无脑吧。
upd:确实无脑。
[CodeChef Danya and Numbers](https://www.codechef.com/problems/DANYANUM)
定义函数 f(x, A),其中 x 是不超过 |A| 的正整数。在计算函数时,我们枚举 A 的所有长度为
x 的子序列,求出子序列中各元素的按位与结果,并选取所有子序列的结果中的最大值作为函数的
值。
这个其实本质上就是去找一个最大的数使得有 $x$ 个 $y \& z = z$。
显然这个 $z$ 可以去枚举 $2^k$,然后顺序加入。
但是怎么维护这个呢,如果这个大于 $500$ (块大小)就重构高维前缀和,其余暴力,检查能否,能的话就加入。
[code](https://www.codechef.com/viewsolution/37215316)
还有一个题是打怪兽的。题目大概是 Codechef:Monster。~~这种玩意难找。只有一个印象。~~
就是问你一只怪兽啥时候会死。
每次对 $x \& y = x$ 的怪兽还是反过来我忘记了(
但是做法一样。
我们对时间戳分块为 $block$。
然后我们枚举 $block$,把该时间内的全部高维前缀和,然后一个个减掉去,如果说有一个减掉了小于0,那么肯定是在这个块里面死掉的,所以就去枚举这个块,由于一个只会死掉一次。
所以复杂度得证。
## 斜率优化。
推推柿子,非常悠闲(
学不会学不会学不会,感觉维护凸包都能李超树。
upd:这搞你呢不会。
## 状压dp。
考虑清楚状态数。
很多时候状压dp 不仅是状压 dp,可以套上容斥,反正可以用啥二项式定理。
## 换根dp。
这个可能会一点皮毛。大概就是考虑 $u \to v$ 的贡献,然后加加减减就可以了。
这个可以放到线段树上面, 遇到过。也能做,做了好几次了。
我成功证明了自己是一个不会 dp 的选手。
# 图论。
## 一些小结论。
**树的中点一定在直径上面。**
upd:这一点没搞上面去。
一颗树如果有两个重心,那么有一条边一定连着两颗 $size = n/2$ 的子树。
离一个点最远的一定是直径端点之一。否则不是直径。反证法可证。(这个反证法实际上是考虑求直径的过程。是要先找到直径的一端。)
~~草这些东西我好像搞上面去了。~~
## 树链剖分。
前置知识:线段树,链式前向星,LCA,DFS序
好了就当你都会了。不会也没关系。
树链剖分通常的操作:
1.x -> y 的路径上修改 2.x -> y 的路径上查询 3. 对于 x 的子树修改 4.对于 x 的子树查询。
一般还有换根操作。树剖也也可以做LCA以及差分操作(但是树剖好像就直接修改了不需要差分)。
树链剖分有两个DFS 这两个DFS就是把一棵树变成一个序列。 然后就可以用数据结构来维护了。
第一个DFS 用来求 $fa$(祖先节点) $size$(子树大小)$son$(重儿子) $d$(深度)
重儿子指的是$size$较大的儿子节点。
第二个DFS 用来求$top$(这条链上最顶端的点) $id$(编号)以及其他的赋值操作。 但是重儿子要先DFS。
```cpp
const int N = 1e5 + 10 ;
struct node { int v , nxt ; } ;
node e[N << 1] ;
int head[N] , cnt = 0 ;
inline void Add(int u , int v) { e[++ cnt].v = v ; e[cnt].nxt = head[u] ; head[u] = cnt ; }
int size[N] , son[N] , d[N] ;
inline void Dfs1(int u) { size[u] = 1 ;
for(register int i = head[u] ; i ; i = e[i].nxt) {
int v = e[i].v ; if(v == fa[u]) continue ; // 防止无限递归。
d[v] = d[u] + 1 , fa[v] = u , // 记录深度 以及父亲节点
Dfs1(v) ; size[u] += size[v] ; //算出子树大小
if(size[v] > size[son[u]]) son[u] = v ; //得出u 的 重儿子是 son[u]
}
}
int top[N] , id[N] , tot = 0 ;
inline void Dfs2(int u , int tp) { top[u] = tp , id[u] = ++ tot ;
if(! son[u]) return ; Dfs2(son[u] , tp) ;
for(register int i = head[u] ; i ; i = e[i].nxt) { int v = e[i].v ;
if(v ^ fa[u] && v ^ son[u]) Dfs2(v , v) ;
}
}
```
这段代码求的就是下图的结果。

对于这张图 $top$ 指的是重链上最靠上的位置。即链的最高处。
$Question:$ 如果对于最右下的那个节点 top 是自己 那么不就死循环了吗 ?
请读者仔细思考这个问题。
假装你会线段树了。
那么我们想 怎么做树上的修改呢?
$id$ 把这个树变成一个序列。
没错 就是`跳链`对于每条重链 你可以一下到顶端 那么你直接修改这条`重链`上的值就可以了(数据结构维护)
万一 一次重链跳不到那里怎么办?
那么说明了这个点并不是重儿子 我们想办法让它跳上去。
反复循环。 DFS1中记录了父亲节点 你将它变成它重链上的最高处的父亲节点。
因为这条重链修改过了 所以不用管重复。一直反复跳 它会跳到 链的 `LCA` 处 这也是为什么可以求`LCA`的原因
对于上面留下的问题…也是一个关于复杂度的证明
假设最坏情况 你的修改/查询的点 没有一条边在重链上 你每次都要 往上 `fa` 一次
但是这种情况 出现在 满多叉树上 这样的话 就是最坏的复杂度 即 $logn$
那么一般还要套一个线段树 所以 最坏的复杂度是 $n log^2 n$
写在最后:如果没有规定根的话 建议根 随机呢 万一弄个满二叉树卡你 你随机一下就可以避免被卡。
`rand()%n+1`
[题都在这](https://www.cnblogs.com/Isaunoya/p/11619823.html)
## kruskal重构树。
重构树的 $1 \to n$ 都是叶子节点,并且是一颗二叉树,满足一些奇怪性质。IOI2018狼人。
一共有 $2n-1$ 个节点。如果节点数不对,那么不连通。不连通的话需要判断 $vis[x]$ 然后 $dfs$ 之类的,略。这个我博客里面也有好几题吧。
**这个上面好像仔细写过,可以往上面翻。**
[1](https://www.cnblogs.com/Isaunoya/p/11780762.html) [2](https://www.cnblogs.com/Isaunoya/p/11983101.html) [3](https://www.cnblogs.com/Isaunoya/p/12363904.html)
## 优化建边。
好多东西可以用来优化建边吧QAQ。前缀优化建边,数据结构优化建边。挺多题的,最经典的还是CF的那题建边+最短路。这个是 [CF786B](https://www.luogu.com.cn/problem/CF786B)
786B 的部分题解:
线段树建图 大概就是这样子…
众所周知 线段树的一个编号 $p$ 指的是 $[L,R]$ 这段区间
```cpp
void buildto(int l , int r , int & p) { // 入边·线段树
if(l == r) { p = l ; return ; }
int mid = l + r >> 1 ; p = ++ cnt ;
buildto(l , mid , ls[p]) ; buildto(mid + 1 , r , rs[p]) ;
add(p , ls[p] , 0) ; add(p , rs[p] , 0) ;
}
```
$p$ 指的是 $[L,R]$ 这段区间的编号
$ls_p$ 指的是 $[L,Mid]$ 这段区间的编号
$rs_p$ 指的是 $[Mid+1,R]$ 这段区间的编号
初始化 $p$ 向 $p$ 的左儿子 和 $p$ 的右儿子连边…
那么就`间接`完成了 $p$ 向 $[L,R]$ 地`单独连边`
即如果对 $p$ 连边 就相当于对 $[L,R]$ 连边…
(~~大概解释的够清楚了?~~)
所以这题可以建两颗线段树 一棵管入边 一棵管出边…
最后跑个最短路就出来了…
这个优化建边也可以用扫描线。有写。好像是一个网络流的。[CF793G](https://www.cnblogs.com/Isaunoya/p/12677485.html)
这里还有一个经典题: [P5471 [NOI2019]弹跳](https://www.luogu.com.cn/problem/P5471)。
但是你需要学会 kdt。
## 长链剖分。
长链剖分遍历一遍的复杂度是 $O(n)$,证明的话大概是 **如果它不是长链,那么它一定是某条长链的 top**,可以用来算一些奇怪的东西,优化dp啥的。[1009F](https://www.cnblogs.com/Isaunoya/p/12378282.html)?
然后有时候可以通过dfn来把信息搞到长链上面,比如说max,min之类的,[150E](https://www.cnblogs.com/Isaunoya/p/12335059.html)自己看吧。
150E 做法挺多的,点分治+单调队列的做法我到现在还没补,那个好像是单调队列按秩合并。
以及 [NOI2020 D1T2] 也是可以长链剖分的,长链剖分可以转移深度相关的 dp。
这个玩意可以去看 Ynoi 的洛谷博客,似乎讲的比较好。
## 单调队列按秩合并。
这个 150E。可能退役前都不会动这一题了吧。
如上,先咕了。以后补上。
## dsu on tree。/树上启发式合并。
dsu on tree 的话挺好用的。每次先遍历轻子树,最后遍历重子树,并保留。这样是对的。
这样的复杂度是 $O(n \log n)$
[在这里](https://www.cnblogs.com/Isaunoya/category/1605082.html)
## 点分治。/ 点分树。
写了好多东西发现自己点分治落下了。
我们考虑先选那么一个重心。然后一直递归下去,层数一定是 log 的,所以就建成了一颗虚拟的点分树。~~(如果这里不懂也没关系毕竟我不是讲算法的)~~
每个部分不会超过 $tot/2$ 不然它不是重心。
重心最多存在两个。
**upd:重心存在两个的条件仅当:两个重心相邻,且最大的儿子都是 tot/2。**
点分治也经常套数据结构。上面说过了一个题,就是点分治和李超树搞起来。
点分树就是把点分治的重心存下来。然后模拟贡献删除?大概是这样。
## 边分治。/ 边分树。
这个还真没学。
听虎说大概是 **三度化然后每次沿一条边把树拆成两半**。
三度化的意思是让每个点度数小于等于 $3$。
咕了咕了。
例题:CTSC2018 暴力写挂
# 数论。
##BSGS
$y^x = z(mod\ p)$ [$p \in prime$]
令
$y^{(x+k)} = z \times y^k(mod\ p)$
然后预处理 $k = [1, \sqrt p]$
BSGS 就是大块枚举 $(x+k)$,就做完了。
##exBSGS
$p \notin prime$
$(A, p) \not| B$ $and$ $B != 1$ 则无解。
令 $G = (A, p)$
使得 $A^{x-1}\frac{A}{G} = \frac{B}{G} (mod \frac{p}{G})$
$A^{x-1} = AB(mod \frac{p}{G}$
递归即可。
```cpp
#include <bits/stdc++.h>
const int mod = 233333;
struct Hash_Table {
Hash_Table() { clear(); }
struct List { int id, val, nxt; } e[233333];
int head[mod], cnt = 0;
void add(int u, int v, int w) { e[++cnt] = {v, w, head[u]}; head[u] = cnt; }
void clear() { memset(head, 0, sizeof(head)); cnt = 0; }
void insert(int x, int i) { int k = x % mod; add(k, x, i); } // mp[x] = i
int query(int x) {
for (int i = head[x % mod]; i; i = e[i].nxt) if (e[i].id == x) return e[i].val;
return -1;
}
} hash;
int qpow(int x, int y, int mod) {
int result = 1;
while (y) {
if (y & 1) { result = 1ll * result * x % mod; }
x = 1ll * x * x % mod; y >>= 1;
}
return result;
}
void NoAnswer() { std::cout << "No Solution" << '\n'; return; }
void exbsgs(int y, int z, int p) {
if (z == 1) { std::cout << 0 << '\n'; return; }
int k = 0, qwq = 1; hash.clear();
for (int g = std::__gcd(y, p); g != 1; g = std::__gcd(y, p)) {
if (z % g) { NoAnswer(); return; }
z /= g; p /= g; ++k;
qwq = 1ll * qwq * (y / g) % p;
if (qwq == z) { std::cout << k << '\n'; return; }
}
int t = sqrt(p) + 1, s = z, base = y;
hash.insert(s, 0);
for (int i = 1; i <= t; i++) { s = 1ll * s * base % p; hash.insert(s, i); }
base = qpow(y, t, p); s = qwq;
for (int i = 1; i <= t; i++) {
s = 1ll * s * base % p;
if (!~hash.query(s)) { continue; }
qwq = hash.query(s);
std::cout << i * t - qwq + k << '\n';
return;
}
NoAnswer();
}
int main() {
std::ios::sync_with_stdio(false);
std::cin.tie(NULL);
int a, p, b;
while (std::cin >> a >> p >> b && a && b && p) { exbsgs(a, b, p); }
return 0;
}
```
## gcd/exgcd。
如果 $\gcd = kx$ 的有 $g_k$ 个,我们可以直接对它做莫比乌斯反演,这样就能得到 $f_k$ (也就是 gcd = k) 的有多少个了。
gcd 复杂度是 $\log$ 的。
https://www.cnblogs.com/Isaunoya/p/12325603.html
还行。
exgcd(a,b,x,y){
if(!y)gcd=x,a=1,b=0;
else exgcd(b,a%b,y,x),y-=(a/b)*x;
}
## 扩展lucas。
$\binom{n}{m} = \binom{n\%p}{m\%p} \times \binom{n/p}{m/p}$
## 扩展欧拉定理。
[P4139 上帝与集合的正确用法](https://www.luogu.com.cn/problem/P4139)
对于 $b \geq \varphi(p)$,有 $a^b = a^{b\ mod\ \varphi(p)\ +\ \varphi(p)} [mod\ p]$
其中 $gcd(a,p)$ 没有要求,也就是可以不互质。
有了这个式子, $2^{2^{2^{2^{2^{2^{2}}}}}} \% \ p$ 就很好求了,递归就可以了,这里的指数 $2^{2^{2^{2^{2^{2}}}}} \geq \varphi(p)$ 的,于是直接用就好了QAQ。递归不会超过 $\log$ 次,所以可以用递归就好了qwq。
```cpp
const int qwq = 1e7;
int phi[qwq + 10];
int qpow(int x, int y, int p) {
int ans = 1;
for (; y; y >>= 1, x = 1ll * x * x % p)
if (y & 1) ans = 1ll * ans * x % p;
return ans;
}
int solve(int p) { return (p == 1) ? 0 : qpow(2, solve(phi[p]) + phi[p], p); }
signed main() {
#ifdef _WIN64
freopen("testdata.in", "r", stdin);
#endif
for (int i = 2; i <= qwq; i++) {
if (phi[i]) continue;
for (int j = i; j <= qwq; j += i) {
if (!phi[j]) phi[j] = j;
phi[j] = phi[j] / i * (i - 1);
}
}
int T;
in >> T;
while (T--) {
int p;
in >> p;
out << solve(p) << '\n';
}
return out.flush(), 0;
}
```
[CF906D Power Tower](https://www.luogu.com.cn/problem/CF906D)
给定 $a \{ \}$ 让你求 $a_l ^ {a_{l+1} ^ {…^{a_r}}}$
然后你会发现 $\varphi(x)$ 在log层的时候会变成 1 ,所以暴力递归就好了,如果觉得慢,可以给 $\varphi$ 加个记忆化。
```cpp
int n, m, q;
vector<int> a;
map<int, int> phi;
int getphi(int x) {
if (phi.count(x)) return phi[x];
int res = x, qwq = x;
for (int i = 2; i <= sqrt(x); ++i)
if (!(x % i)) {
res = res / i * (i - 1);
while (!(x % i)) x /= i;
}
if (x > 1) res = res / x * (x - 1);
return phi[qwq] = res;
}
int mod(int x, int p) { return (x < p) ? x : (x % p + p); }
int qpow(int x, int y, int p) {
int ans = 1;
for (; y; y >>= 1, x = mod(x * x, p))
if (y & 1) ans = mod(ans * x, p);
return ans;
}
int dfs(int l, int r, int p) {
if (l == r || p == 1) return mod(a[l], p);
return qpow(a[l], dfs(l + 1, r, getphi(p)), p);
}
signed main() {
#ifdef _WIN64
freopen("testdata.in", "r", stdin);
#endif
in >> n >> m;
a.resize(n);
for (int i = 0; i < n; i++) in >> a[i];
in >> q;
while (q--) {
int l, r;
in >> l >> r;
--l, --r;
out << dfs(l, r, m) % m << '\n';
}
return out.flush(), 0;
}
```
## crt/excrt
考虑若干个等式,$x = res_i (mod\ mod_i)$
我们考虑到,前 $i-1$ 个式子是可以合并成 $bx + a$ 形式的,即 $x = a (mod\ b)$
然后搞一个等式,$bx + a = res_i (mod\ mod_i)$
移项,变成 (ax + by) 形式即 $b * x + mod_i * y = res_i - a$
根据 exgcd 只能求出来 $ax + by = \gcd(a,b)$ 符合条件的一组 $(x,y)$
显然如果 $res_i - a = 0 (mod\ gcd)$ 才会有解。
我们把 $x, y$ 乘上 $\frac{(res_i - a)}{gcd}$
那么此时的 $x, y$ 满足 $b * x + mod_i * y = res_i - a$
令 $t = lcm(b, mod_i)$
$(a+bx)\%t$ 显然是符合条件的解,并且符合两个条件。
所以合并之后的 $a$ 是 $(a+bx)\%t$,$b = lcm(b, mod_i)$
```cpp
typedef __int128 ll;
signed main() {
ios::sync_with_stdio(false);
cin.tie(nullptr), cout.tie(nullptr);
auto excrt = [&](vector <long long> res, vector <long long> mod, int n) {
// x % mod = res
function <void(ll, ll, ll&, ll&)> exgcd = [&](ll a, ll b, ll&x, ll&y) {
if(!b) { x = 1; y = 0; return; }
exgcd(b, a % b, y, x), y -= x * (a / b);
};
function <ll(ll, ll)> gcd = [&](ll a, ll b) {
if(!b) return a;
return gcd(b, a % b);
};
ll a = res[0], b = mod[0], x, y, g, t;
for(int i = 1; i < n; i++) {
exgcd(b, mod[i], x, y), g = gcd(b, mod[i]);
if((res[i] - a) % g) { return (ll)-1ll; }
x = (x * (res[i] - a) / g) % mod[i];
cout << (long long)x << ' ' << (long long)y << '\n';
t = b / g * mod[i];
a = ((a + b * x) % t + t) % t;
b = t;
}
return (ll)(a % b + b) % b;
};
cout << (long long)excrt(res, mod, n) << '\n';
return 0;
}
```
## 矩阵快速幂。
~~我们考虑线性代数上面的矩阵知识~~
啊呸,是基础数学
斐波那契的矩阵就不讲了
定义矩阵 $f_x$ 是第 $x$ 项的斐波那契矩阵
因为
$f_i * f_j = f_{i+j}$
然后又因为 $\texttt{AB+AC=A(B+C)}$
所以 $\sum_{i=l}^{r} f(a_i+x) = f(x)\sum_{i=l}^{r} f(a_i)$
线段树板子题,维护一个矩阵,这题没了
```cpp
const int mod = 1e9 + 7 ;
const int maxn = 1e5 + 51 ;
struct matrix {
int a[3][3] ;
matrix () {
rep(i , 1 , 2) rep(j , 1 , 2) a[i][j] = 0 ;
}
void clr() {
rep(i , 1 , 2) rep(j , 1 , 2) a[i][j] = 0 ;
rep(i , 1 , 2) a[i][i] = 1 ;
}
bool empty() {
if(a[1][1] ^ 1) return false ;
if(a[1][2] || a[2][1]) return false ;
if(a[2][2] ^ 1) return false ;
return true ;
}
matrix operator * (const matrix & other) const {
matrix res ;
rep(i , 1 , 2) rep(j , 1 , 2) {
res.a[i][j] = 0 ;
rep(k , 1 , 2) res.a[i][j] = (res.a[i][j] + a[i][k] * other.a[k][j]) % mod ;
}
return res ;
}
matrix operator + (const matrix & other) const {
matrix res ;
rep(i , 1 , 2) rep(j , 1 , 2) res.a[i][j] = (a[i][j] + other.a[i][j] >= mod) ? a[i][j] + other.a[i][j] - mod : a[i][j] + other.a[i][j] ;
return res ;
}
} ;
matrix qwq ;
matrix qpow(matrix a , int k) {
matrix res = a ; -- k ;
for( ; k ; a = a * a , k >>= 1)
if(k & 1) res = res * a ;
return res ;
}
int n , m ;
int a[maxn] ;
matrix s[maxn << 2] , tag[maxn << 2] ;
void build(int l , int r , int o) {
tag[o].clr() ;
if(l == r) {
s[o] = qpow(qwq , a[l]) ;
return ;
}
int mid = l + r >> 1 ;
build(l , mid , o << 1) ;
build(mid + 1 , r , o << 1 | 1) ;
s[o] = s[o << 1] + s[o << 1 | 1] ;
}
void psd(int o) {
if(tag[o].empty()) return ;
tag[o << 1] = tag[o << 1] * tag[o] ;
tag[o << 1 | 1] = tag[o << 1 | 1] * tag[o] ;
s[o << 1] = s[o << 1] * tag[o] ;
s[o << 1 | 1] = s[o << 1 | 1] * tag[o] ;
tag[o].clr() ;
}
void upd(int a , int b , int l , int r , matrix x , int o) {
if(a <= l && r <= b) {
s[o] = s[o] * x ;
tag[o] = tag[o] * x ;
return ;
}
psd(o) ;
int mid = l + r >> 1 ;
if(a <= mid) upd(a , b , l , mid , x , o << 1) ;
if(b > mid) upd(a , b , mid + 1 , r , x , o << 1 | 1) ;
s[o] = s[o << 1] + s[o << 1 | 1] ;
}
matrix qry(int a , int b , int l , int r , int o) {
if(a <= l && r <= b) {
return s[o] ;
} psd(o) ;
int mid = l + r >> 1 ;
matrix res ;
if(a <= mid) res = res + qry(a , b , l , mid , o << 1) ;
if(b > mid) res = res + qry(a , b , mid + 1 , r , o << 1 | 1) ;
return res ;
}
signed main() {
#ifdef _WIN64
freopen("testdata.in" , "r" , stdin) ;
#endif
qwq.a[1][1] = qwq.a[1][2] = qwq.a[2][1] = 1 ;
qwq.a[2][2] = 0 ;
in >> n >> m ;
rep(i , 1 , n) in >> a[i] ;
build(1 , n , 1) ;
while(m --) {
int opt ;
in >> opt ;
if(opt == 1) {
int l , r , v ;
in >> l >> r >> v ;
upd(l , r , 1 , n , qpow(qwq , v) , 1) ;
}
else {
int l , r ;
in >> l >> r ;
out << qry(l , r , 1 , n , 1).a[1][2] << '\n' ;
}
}
return out.flush(), 0;
}
```
## 组合数。
AGC001 E - BBQ Hard
这题就是要求
$\sum_{i=1}^{n} \sum_{j=i+1}^{n} C(a_i+a_j+b_i+b_j,a_i+a_j)$
考虑搞一搞,$C(a_i+a_j+b_i+b_j,a_i+a_j)$的意义等同于从 $(-a_j,-b_j)$ 走到 $(a_i,b_i)$
的方案数
因而其他的走到 $(a_i,b_i)$ 的步数就等于所有的加起来走到$(a_i,b_i)$
然后就可以了
考虑多余的部分
$\sum_{i=1}^{n} \sum_{j=i+1}^{n} C(a_i+a_j+b_i+b_j,a_i+a_j)$
$=\frac{\sum_{i=1}^{n} \sum_{j=1}^{n} C(a_i+a_j+b_i+b_j,a_i+a_j)-\sum_{i=1}^{n} C(a_i+a_i,b_i+b_i)}{2}$
逆元搞一搞,没了。
```cpp
int n ;
const int N = 2e5 + 10 ;
int a[N] , b[N] ;
const int S = 2e3 + 1 ;
const int M = 4e3 + 20 ;
int dp[M][M] ;
int fac[S << 2] ;
const int mod = 1e9 + 7 ;
int qpow(int x , int y) {
int ans = 1 ;
for( ; y ; y >>= 1 , x = x * x % mod)
if(y & 1) ans = ans * x % mod ;
return ans ;
}
int inv(int x) {
return qpow(x , mod - 2) ;
}
int C(int x , int y) {
return fac[x] % mod * inv(fac[y]) % mod * inv(fac[x - y]) % mod ;
}
signed main() {
ios :: sync_with_stdio(false) ;
cin.tie(0) ;
cout.tie(0) ;
cin >> n ;
fac[0] = 1 ;
rep(i , 1 , S << 2) fac[i] = fac[i - 1] * i % mod ;
rep(i , 1 , n) cin >> a[i] >> b[i] ;
rep(i , 1 , n) ++ dp[S - a[i]][S - b[i]] ;
rep(i , 1 , S << 1) rep(j , 1 , S << 1) {
dp[i][j] = (dp[i][j] + dp[i][j - 1]) % mod ;
dp[i][j] = (dp[i][j] + dp[i - 1][j]) % mod ;
}
int ans = 0 ;
rep(i , 1 , n) (ans += dp[S + a[i]][S + b[i]]) %= mod ;
rep(i , 1 , n) {
ans = (ans - C(a[i] + b[i] + a[i] + b[i] , a[i] + a[i]) + mod) % mod ;
}
ans = (ans * inv(2)) % mod ;
cout << ans << '\n' ;
return 0 ;
}
```
CF756D 【Bacterial Melee】
首先定义一个状态 $dp_{j,c}$ 表示选了 $j$ 个位置最后一个字符是 $c$。
转移方程是
$dp_{j,c} = \sum dp_{j-1,k} [k \neq c]$
代表的是长度为 $j$ 的以 $c$ 结尾的方案数…
然后你发现,这个其实可以把 abc 变成 aab 的,所以很显然…是跟断点数量有关,假设你有 $m$ 个断点,你发现你选的这个其实是个组合数 $(^n_m)$ 其实证明就是当做断点来看,然后每次你枚举长度,倒序枚举,大概是01背包的那种想法,把不相同的全部加进来…这样就做完了。
```cpp
const int maxn = 5e3 + 35;
const int mod = 1e9 + 7;
int C[maxn][maxn];
int dp[maxn][27];
int add(int x, int y) {
return (x + y >= mod) ? (x + y - mod) : (x + y);
}
signed main() {
string s;
vector<int> a;
ios :: sync_with_stdio(false);
cin.tie(nullptr), cout.tie(nullptr);
int len; cin >> len; cin >> s;
a.clear(); a.push_back(0);
for(char x: s) {
int c = x - 'a' + 1;
if(c == a.back()) continue;
a.push_back(c);
}
int n = len;
C[0][0] = 1;
for(int i = 1 ; i <= n ; i ++) {
for(int j = 1 ; j <= i ; j ++) { C[i][j] = add(C[i - 1][j], C[i - 1][j - 1]); }
}
dp[0][0] = 1;
for(int i = 1 ; i < a.size() ; i ++) {
for(int j = i ; j ; j --) {
int x = a[i], ans = 0;
for(int c = 0; c <= 26; c ++) { if(c ^ x) { ans = add(ans, dp[j - 1][c]); } }
dp[j][x] = ans;
}
}
int ans = 0;
for(int i = 1 ; i < a.size(); i ++) {
int tmp = 0;
for(int c = 1 ; c <= 26 ; c ++) tmp = add(tmp, dp[i][c]);
ans = add(ans, 1ll * C[n][i] * tmp % mod);
}
cout << ans << '\n';
return 0;
}
```
## 拉格朗日插值的公式。
$f(k) = \sum_{i=0}^{n}y_i \prod_{j!=i} \frac{k-x_j}{x_i-x_j}$
$x_i,y_i$ 是在 $x_i$ 的取值。
```cpp
const int mod = 998244353;
int qpow(int x, int y) {
int res = 1;
for(; y; y >>= 1, x = x * x % mod)
if(y & 1) res = res * x % mod;
return res;
}
int inv(int x) { return qpow(x, mod - 2); }
int n, k;
const int maxn = 2e3 + 32;
int x[maxn], y[maxn];
#define out cout
signed main() {
#ifdef LOCAL
#define in cin
ios :: sync_with_stdio(false), cin.tie(nullptr), cout.tie(nullptr);
freopen("testdata.in", "r", stdin);
#else
io in;
#endif
in >> n >> k;
for(int i = 1 ; i <= n ; i ++) in >> x[i] >> y[i];
int ans = 0;
for(int i = 1 ; i <= n ; i ++) {
int a, b; a = b = 1;
for(int j = 1 ; j <= n ; j ++) if(i ^ j) { a = a * (k - x[j]) % mod; }
for(int j = 1 ; j <= n ; j ++) if(i ^ j) { b = b * (x[i] - x[j]) % mod; }
a = (a + mod) % mod, b = (b + mod) % mod, b = inv(b);
ans = (ans + a * b % mod * y[i] % mod) % mod;
}
out << ans << '\n';
return 0;
}
```
## 线性基
我现在大概理解线性基了。
假设你有一个集合 $S$,那你可以把它压成一个线性基 $P$,然后使得两个集合能异或出来的玩意完全一致。
我们是要按位操作。
假设你 $S = \{1,2,3\}$,那你发现你的 $P = \{1,2\}$ 是可以的。
然后 $\{1,3\}$ 也是可以的。你要明白线性基这玩意不唯一,而且他是不同顺序可能会有多种不同的线性基。
说几个有用的性质先。
- 线性基有 $\log$ 位,每一位 $p_i$ 的最高位是 $2^i$ 或者不存在该位
- 因为高位不冲突,所以能构造的数字自然是 $2^{|P|}-1$ 个啦!
我们想象一下线性基的过程。线性基一共有 $\log$ 位对不对。
我们考虑如果 $x$ 的最高位为 $2^i$ ,如果 $p_i$ 是 0,也就是空的基的话。
我们就直接把 $p_i = x$,这样丢进去就好了/cy。
那么如果 $p_i != 0$ 怎么办,我们考虑到,如果 $p_i$ 是插进去的话,那么他也是原来的元素之一,所以和他异或一下还能是原集合能异或出来的数。
但是如果他是间接插进去的怎么办,它异或过其他数字!不用慌,转化一下,由于那个位置是若干个原集合 $S$ 的元素异或得来,当你插入这个元素,和原集合的元素异或的时候,它还是原集合能异或出来的数字对不对。
所以你整个集合都是原集合能异或出来的数字构成的,在特殊情况下,它其实就是原集合的数构成的,当你顺序插入的时候。
所以先异或上,然后你的最高位就没掉了,接着向下循环,直到能插进去位置,如果他插不进去?为什么呢,因为它会变成 $0$。
因为你每一位都是可以**控制**的,控制的意思大概是指,你的 $i$ 位如果有元素,那么你可以选择这一位 $2^i$ 是选还是不选,记住,此时你只关心这个最高位。也就是从高位贪心。
如何证明线性基的元素都能异或出来原集合的元素呢?
- 线性基的元素是由原集合构造出来的。
- 原集合有些元素是冲突的,而线性基并没有插入进去线性相关的元素,即能把它扔进去变为0的元素。
我们再考虑,如果你丢进去 $\{6,10\}$,你发现你只能异或出来 ${6,10,12}$ 对吧。
你发现如果你丢到线性基里,你的线性基元素也是 $\{6,10\}$,还是只能构造出来这么多。
但是如果你原集合是 $\{6,10,12\}$ 呢?你考虑到,你丢进去6,插入成功了,线性基 $\{6\}$
然后再插入10,显然能丢进去对吧,线性基 $\{6,10\}$,然后我们发现原集合能构造出来是 $\{6,10,12\}$,而你线性基构造出来的还是 $\{6,10,12\}$。
假如,我们要求一个数字,能不能被一个这个集合表示,怎么办,我们就假装插入~~(雾)~~
按照插入的姿势,直接丢进去,看有没有一个位置为空,如果有一个位置为空的,直接return 1就好了,否则就return 0
- 如何求最大值
假设原集合能异或出来的数字,线性基也能异或出来,你懂了的话。最大值似乎也不是什么问题。
我们发现 $p_i$ 的最高位是 $2^i$ 对吧,且其他元素的最高位都不和这个重复。
我们倒着取(这里指倒着循环),如果 $p_i$ 这一位存在,我们自然是不取这一个基的,否则就取过来,因为你一个 $2^i \geq p_{i-1}$,易证,不证明了。
然后你可以有效的控制 $2^i$ 这一位到底有没有,因为你 $p_i$ 一定存在 $i$ 这一位,但是你 $p_j [j \geq i]$ 也可能存在 $i$ 这一位所以不能直接取,要取一个 $max(ans , ans \oplus p_i)$。
如果我们想求 $k$ 大 $k$ 小的话,那么我们要去关心 $i$ 必须不能被比他大的元素干扰,所以我们要消除这个贡献也就是 $p_i \& (2^j) [j < i]$ 的时候 $p_i \oplus p_j$
[LOJ 有个题可以去试试](https://loj.ac/problem/114)
代码长这个样子
[P3812 【模板】线性基
](https://www.luogu.com.cn/problem/P3812)
```cpp
int n, a[64], p[64];
signed main() {
#ifdef _WIN64
freopen("testdata.in", "r", stdin);
#endif
in >> n;
rep(i, 1, n) in >> a[i];
rep(i, 1, n) {
for (int j = 50; ~j; --j) {
if ((a[i] & (1ll << j))) {
if (!p[j]) p[j] = a[i];
a[i] ^= p[j];
}
}
}
int ans = 0;
for (int i = 50; ~i; --i) ans = max(ans, ans ^ p[i]);
out << ans << '\n';
return out.flush(), 0;
}
```
[P4151 [WC2011]最大XOR和路径](https://www.luogu.com.cn/problem/P4151)
找个出所有简单环,这样就可以和原有路径抵消掉
最后求异或,没了
```cpp
int n, m;
const int N = 5e4 + 10;
const int M = 1e5 + 10;
int cnt = 0, head[N];
struct Edge {
int v, nxt, w;
} e[M << 1];
int d[N], p[65];
bool vis[N];
void add(int u, int v, int w) {
e[++cnt] = { v, head[u], w }, head[u] = cnt;
e[++cnt] = { u, head[v], w }, head[v] = cnt;
}
void insert(int val) {
for (int i = 63; ~i; --i)
if (val & (1ll << i)) {
if (!p[i]) p[i] = val;
val ^= p[i];
}
}
void dfs(int u, int cur) {
d[u] = cur, vis[u] = 1;
for (int i = head[u]; i; i = e[i].nxt) {
int v = e[i].v;
if (vis[v])
insert(cur ^ e[i].w ^ d[v]);
else
dfs(v, cur ^ e[i].w);
}
}
int query(int val) {
int res = val;
for (int i = 63; ~i; --i) cmax(res, res ^ p[i]);
return res;
}
signed main() {
#ifdef _WIN64
freopen("testdata.in", "r", stdin);
#endif
in >> n >> m;
int u, v, w;
while (m--) {
in >> u >> v >> w, add(u, v, w);
}
dfs(1, 0);
out << query(d[n]) << '\n';
return out.flush(), 0;
}
```
## 莫比乌斯反演。&欧拉反演。
$\sum_{d|n} \mu(d) = [n == 1]$
$\sum_{d|n} \varphi(d) = n$
这个第二个结论可以搞个题目。比如说 [P6624 [省选联考 2020 A 卷] 作业题](https://www.luogu.com.cn/problem/P6624)。
### P6624 [省选联考 2020 A 卷] 作业题
看到这个柿子
$val(T) = {\large{\left(\sum_{i=1}^{n-1} w_{e_i}\right)}} \times \gcd(w_{e1}, w_{e2},...,w_{e_{n-1}})$
首先考虑欧拉反演。
$x = \sum_{d|x} \varphi(d)$
然后原式变成
$val(T) = {\large{\left(\sum_{i=1}^{n-1} w_{e_i}\right)}} \times \sum_{d| \gcd(w_{e1}, w_{e2},...,w_{e_{n-1}})} \varphi(d)$
枚举 $d$
$\sum_{d} \varphi(d) \times \sum_T {\large{\left(\sum_{i=1}^{n-1} w_{e_i}\right)}}$
然后我们只关心这个部分 $\sum_T {\large{\left(\sum_{i=1}^{n-1} w_{e_i}\right)}}$ 怎么算。
众所周知普通的矩阵树定理只适用于求 $\sum_T \prod (w_{e_1}, w_{e_2}, ..., w_{e_{n-1}})$
(所以如果想求生成树个数直接令所有的边 $w=1$)
然后这题的重要套路就出来了。
我们定义一个 $1+w_ix$
$\prod_{i} (1+w_ix)$ 的一次项系数就是这个 $\sum$ 的值。
这样的话其他项就没什么作用了。
意思是我们只需要维护一个常数项和一次项就够了。
然后变成了多项式操作。
```cpp
// x 是常数项, y 是一次项系数。
inline pair operator+(pair a, pair b) {
static pair res;
res.x = (a.x + b.x) % MOD;
res.y = (a.y + b.y) % MOD;
return res;
}
inline pair operator-(pair a, pair b) {
static pair res;
res.x = (a.x - b.x + MOD) % MOD;
res.y = (a.y - b.y + MOD) % MOD;
return res;
}
inline pair operator*(pair a, pair b) {
static pair res;
res.x = 1ll * a.x * b.x % MOD;
res.y = (1ll * a.x * b.y + 1ll * a.y * b.x) % MOD;
return res;
}
inline pair operator/(pair a, pair b) {
static pair res;
int iv = qpow(b.x, MOD - 2);
res.x = 1ll * a.x * iv % MOD;
res.y = ((1ll * a.y * b.x - 1ll * a.x * b.y) % MOD + MOD) % MOD * iv % MOD * iv % MOD;
return res;
}
```
我们发现这个加法和减法都很 simple。
这个乘法直接展开就行了,这个除法的话有点难理解。
$\frac{a + bx}{c + dx} = \frac{a}{c} + \frac{bc - ad}{c^2}x$
然后常数项和这个都出来了。
这个怎么求出来的呢?~~多项式求逆~~
我们先求出来 $\frac{1}{c+dx}$,然后再乘起来。
令 $C+Dx = \frac{1}{c+dx}$。
即 $(C+Dx)(c+dx) = 1 (\mod x^2)$
$C \times c = 1$ 即 $C = \frac{1}{c}$
因为 $Cdx + cDx = 0$
$\frac{d}{c} + cD = 0$,$D = -\frac{d}{c^2}$
然后 $(a+bx) (C+Dx) = (a+bx)\frac{1}{c+dx} = \frac{a}{c} + \frac{bc - ad}{c^2}x$
就没了。
[代码看这里吧](https://www.luogu.com.cn/blog/Isaunoya/solution-p6624)
给几个题:尝试用莫比乌斯反演和欧拉反演推一推。
有几个小技巧是枚举公约数,然后提取 $\mu_k$ 这部分,然后一整块计算。
$\sum \sum \gcd(i,j)==1$
$\sum \sum \gcd(i,j)$
$\sum \sum lcm(i,j)$
$\prod \prod lcm(i,j)$
$\prod \prod f(\gcd(i,j))^{\gcd(i,j)}$
入门题: [AGC038C](https://www.luogu.com.cn/problem/AT5200)
设 $cnt_i$ 为 $i$ 的出现次数。
则这题要求的是 $\sum_{i=1}^{N} \sum_{j=1}^{N} lcm(i, j) \times cnt_i \times cnt_j$
$\left( lcm (i,j) = \frac{ij}{\gcd(i,j)}\right)$
$\sum_{i=1}^{N} \sum_{j=1}^{N} \frac{ij}{\gcd(i,j)} \times cnt_i \times cnt_j$
枚举 $\gcd$。
$\sum_{d=1}^{N} \sum_{i=1}^{N/d} \sum_{j=1}^{N/d} [\gcd(i,j) =1]d\times ij\times cnt_{id} \times cnt_{jd}$
$\sum_{k|n} \mu_k = [n==1]$
$\sum_{d=1}^{N} \sum_{i=1}^{N/d} \sum_{j=1}^{N/d} \sum_{k|\gcd(i,j)}\mu_k \times d\times ij\times cnt_{id} \times cnt_{jd}$
枚举 $k$。
$\sum_{d=1}^{N} \sum_{k=1}^{N/d}\sum_{i=1}^{n/kd}\sum_{j=1}^{n/kd}\mu_k \times d \times k^2 \times i \times j \times cnt_{idk} \times cnt_{jdk}$
$T = dk$。
$\sum_{T=1}^{N} T \times \left(\sum_{i=1}^{N/T} i \times cnt_{iT}\right)^2 \sum_{k|T} \mu_k \times k$
然后就做完了。
基础题:[这里](https://www.luogu.com.cn/blog/Isaunoya/solution-p6156)。
给个毒瘤题大概就会熟练运用莫比乌斯反演了。
[这里](https://www.luogu.com.cn/problem/P4240)
神仙莫比乌斯反演。
有个结论。
$\varphi(i\times j) = \huge{\left(\frac{\varphi(i) \times \varphi(j) \times \gcd(i,j)}{\varphi(\gcd(i,j))}\right)}$
首先假设 $n\leq m$
$\sum_i \sum_j \varphi(i\times j) = \sum_i \sum_j {\large \left(\frac{\varphi(i) \times \varphi(j) \times \gcd(i,j)}{\varphi(\gcd(i,j))}\right)}$
枚举$\gcd$!
$\sum_d \sum_i \sum_j \frac{\varphi(i) \times \varphi(j) \times \gcd(i,j)}{\varphi(\gcd(i,j))}[\gcd(i,j) = d]$
然后
$\sum_d {\left(\frac{d}{\varphi(d)}\right)} \sum_i^{\frac{n}{d}} \sum_j^{\frac{m}{d}}\varphi(i\times d) \varphi(j\times d)[\gcd(i,j) = 1]$
发现 $\gcd$ 可以用 $\mu$ 搞
$\sum_{d|x} \mu(d) = [x=1]$
$\sum_d {\left(\frac{d}{\varphi(d)}\right)}\sum_i^{\frac{n}{d}} \sum_j^{\frac{m}{d}}\varphi(i\times d) \varphi(j\times d){\left(\sum_{k|\gcd(i,j)} \mu(k)\right)}$
然后顺手枚举一波 $k$!
$\sum_d {\left(\frac{d}{\varphi(d)}\right)} \sum_{k}^{\frac{n}{d}}\mu(k) \sum_{i}^{\frac{n}{kd}}\sum_j^{\frac{m}{kd}}\varphi(i\times kd) \times \varphi(j \times kd)$
改变枚举顺序,令 $T=k\times d$
$\sum_T \sum_{d|T} \mu(\frac{T}{d}) \frac{d}{\varphi(d)} \sum_i^{\frac{n}{T}} \sum_j^{\frac{m}{T}} \varphi(i\times T) \times \varphi(j\times T)$
然后我们搞搞 $F(T) = \sum_T \sum_{d|T} \mu(\frac{T}{d}) \frac{d}{\varphi(d)}$
$(T, n, m) = \sum_i^{\frac{n}{T}} \sum_j^{\frac{m}{T}} \varphi(i\times T) \times \varphi(j\times T)$
发现其实可以令 $G(x, y) = \sum_i^x \varphi(i\times y)$
$G(x, y) = G(x - 1, y) + \varphi(xy)$
然后整个式子就变成了 $\sum_T F(T)\times G(\frac{n}{T},T) \times G(\frac{m}{T},T)$
$G$ 可以直接暴力算,因为这个玩意是调和级数的。
但是发现这个答案数组不能搞得太大,所以需要一个根号分治,$\leq B$ 的部分暴力,$\geq B+1$ 的整除分块。
## 杜教筛。
杜教筛通常搞一些积性函数前缀和。
原理是整除分块套娃,然后复杂度是对的(
可以通过推柿子得出。
给出两个题目
[1](https://www.cnblogs.com/Isaunoya/p/12246398.html)
$$\sum_{i=1}^{n}\sum_{j=1}^{n} ij\gcd(i,j)$$
$$=\sum_{d=1}^{n} d \sum_{i=1}^{n}\sum_{j=1}^{n} ij[\gcd(i,j)==d]$$
$$=\sum_{d=1}^{n} d^3 \sum_{i=1}^{\lfloor\frac{n}{d}\rfloor} \sum_{j=1}^{\lfloor\frac{n}{d}\rfloor} ij[\gcd(i,j)==1]$$
$$=\sum_{d=1}^{n} d^3 \sum_{i=1}^{\lfloor\frac{n}{d}\rfloor} \sum_{j=1}^{\lfloor\frac{n}{d}\rfloor} ij[\gcd(i,j)==1]$$
因为 $\sum_{t|n} \mu(t) = [n == 1]$
所以
$$=\sum_{d=1}^{n} d^3 \sum_{i=1}^{\lfloor\frac{n}{d}\rfloor} \sum_{j=1}^{\lfloor\frac{n}{d}\rfloor} ij \sum_{t|\gcd(i,j)} \mu(t)$$
$$=\sum_{d=1}^{n} d^3 \sum_{t=1}^{\lfloor\frac{n}{d}\rfloor} \mu(t) t^2 \sum_{i=1}^{\lfloor\frac{n}{td}\rfloor} \sum_{j=1}^{\lfloor\frac{n}{td}\rfloor} ij$$
设 $sum_x = \sum_{i=1}^{x}$
则原式等同于
$$=\sum_{d=1}^{n} d^3 \sum_{t=1}^{\lfloor\frac{n}{d}\rfloor} \mu(t) t^2 (sum_{\lfloor \frac{n}{td} \rfloor})^2$$
设 $T=td$
$$=\sum_{T=1}^{n} T^2 (sum_{\lfloor \frac{n}{T} \rfloor})^2 \sum_{d|t} \mu (\frac{T}{d}) d $$
因为
$$\sum_{d|n} \frac{\mu(d)}{d} = \frac{\varphi(n)}{n}$$
根据狄利克雷卷积
$$id(x) = x , id * \mu = \varphi$$
那么这个柿子变成了
$$\sum_{T=1}^{n}T^2 \varphi(T) (sum_{\lfloor \frac{n}{T} \rfloor})^2$$
然后我们本身知道 形如 $\lfloor \frac{n}{T} \rfloor$ 之类的玩意可以数论分块
然后 $f_x = x^2 \varphi(x)$ 的前缀和
设 $s_x$ 是 $f_x$ 的前缀和,然后考虑 $g$ 函数
然后我们知道
$$\sum_{d|n} \varphi(d) = n$$
考虑 $g$ 函数为 $g_i = i^2$
$$(g*f)(i) = \sum_{d|i} d^2 \varphi (d) \frac{i^2}{d^2} = \sum_{d|i}\varphi (d) i^2 = i^3$$
$$s_n = \sum_{i=1}^{n} i^3 - \sum_{i=2}^{n} i^2 s_{\frac{n}{i}}$$
因为
$$\sum_{i=1}^{n}i^3 = (\sum_{i=1}^{n}i)^2$$
$$\sum_{i=1}^{n}i^2 = \frac{n(n+1)(2n+1)}{6}$$
Q.E.D.
杜教筛一手,这题没了。
```cpp
int n , p ;
const int maxn = 5e6 + 10 ;
int phi[maxn + 5] ;
int iv2 , iv6 ;
int qpow(int x , int y) {
int res = 1 ;
for( ; y ; y >>= 1 , x = x * x % p)
if(y & 1)
res = res * x % p ;
return res ;
}
int sum(int x) {
x = x - (x / p) * p ;
return (x + 1) * x % p * iv2 % p ;
}
int sum2(int x) {
x = x - (x / p) * p ;
return (x + 1) * x % p * (x + x + 1) % p * iv6 % p ;
}
unordered_map < int , int > _phi ;
int s(int x) {
if(x <= maxn) return phi[x] ;
if(_phi[x]) return _phi[x] ;
int ans = sum(x) ;
ans = ans * ans % p ;
for(int l = 2 , r ; l <= x ; l = r + 1) {
r = x / (x / l) ;
ans = (ans - (sum2(r) - sum2(l - 1) + p) % p * s(x / l) % p + p) % p ;
}
return _phi[x] = ans ;
}
signed main() {
#ifdef _WIN64
freopen("testdata.in" , "r" , stdin) ;
#else
ios_base :: sync_with_stdio(false) ;
cin.tie(nullptr) , cout.tie(nullptr) ;
#endif
// code begin.
in >> p >> n ;
iv2 = qpow(2 , p - 2) ;
iv6 = qpow(6 , p - 2) ;
phi[1] = 1 ;
for(int i = 2 ; i <= maxn; i ++) {
if(phi[i])
continue ;
for(int j = i ; j <= maxn ; j += i) {
if(! phi[j])
phi[j] = j ;
phi[j] = phi[j] / i * (i - 1) ;
}
}
for(int i = 1 ; i <= maxn ; i ++)
phi[i] = (phi[i - 1] + 1ll * i * i % p * phi[i] % p) % p ;
int ans = 0 ;
for(int l = 1 , r ; l <= n ; l = r + 1) {
r = n / (n / l) ;
int k = sum(n / l) ;
k = k * k % p ;
ans = (ans + (s(r) - s(l - 1) + p) % p * k % p) % p ;
}
out << ans << '\n' ;
return out.flush() , 0 ;
// code end.
}
```
[2](https://www.cnblogs.com/Isaunoya/p/12267408.html)
没啥好说的,杜教筛板子题。
$$\sum_{i=1}^{N} \sum_{j=1}^{N}\sum_{p=1}^{\lfloor \frac{N}{j} \rfloor}\sum_{q=1}^{\lfloor \frac{N}{j} \rfloor} [\gcd(i,j)==1][\gcd(p,q)==1]$$
容易发现,我们枚举 $j$ 其实是相当于枚举 $\gcd$
~~才不是枚举题目~~
然后式子可以变成
$$\sum_{i=1}^{N}\sum_{p=1}^{N}\sum_{q=1}^{N} [\gcd(i,p,q)==1]$$
然后套路式的枚举 $gcd$ ~~依旧不是枚举题目~~
$$\sum_{d=1}^{N}\sum_{i=1}^{N}\sum_{p=1}^{N}\sum_{q=1}^{N}[\gcd(i,p,q)==d]$$
熟悉的形式,其实就等于
$$\sum_{d=1}^{N}\sum_{i=1}^{\lfloor \frac{N}{d} \rfloor} \sum_{p=1}^{\lfloor \frac{N}{d} \rfloor} \sum_{q=1}^{\lfloor \frac{N}{d} \rfloor} \mu(d)$$
$$\sum_{d=1}^{N} \mu(d) \lfloor \frac{N}{d}\rfloor^3$$
然后整除分块就完了,由于 $N$ 比较大,大力杜教筛就完事了,~~话说我好像是这题除掉出题人的最优解~~
```cpp
const int maxn = 5e5 ;
int mu[maxn + 10] ;
const int mod = 998244353 ;
map < int , int > _mu ;
int getmu(int x) {
if(x <= maxn) return mu[x] ;
if(_mu[x]) return _mu[x] ;
int ans = 1 ;
int l = 2 , r = 0 ;
for( ; l <= x ; l = r + 1) {
r = x / (x / l) ;
ans -= getmu(x / l) * (r - l + 1) ;
ans = (ans + mod) % mod ;
}
return _mu[x] = ans ;
}
signed main() {
#ifdef _WIN64
freopen("testdata.in" , "r" , stdin) ;
#else
ios_base :: sync_with_stdio(false) ;
cin.tie(nullptr) , cout.tie(nullptr) ;
#endif
// code begin.
mu[1] = 1 ;
for(int i = 1 ; i <= maxn ; i ++)
for(int j = i + i ; j <= maxn ; j += i)
mu[j] -= mu[i] ;
for(int i = 2 ; i <= maxn ; i ++)
mu[i] = (mu[i] + mu[i - 1]) % mod ;
int n ;
in >> n ;
int l = 1 , r = 0 ;
int ans = 0 ;
for( ; l <= n ; l = r + 1) {
r = n / (n / l) ;
int qwq = (n / l) * (n / l) % mod * (n / l) % mod ;
ans = (ans + (getmu(r) - getmu(l - 1) + mod) % mod * qwq % mod) % mod ;
}
out << ans << '\n' ;
return out.flush() , 0 ;
// code end.
}
```
## 斯特林数。
## 第一类斯特林数。
$\begin{bmatrix}n\\m\end{bmatrix}$ 表示第一类斯特林数。
其组合意义是 $n$ 个元素分成 $m$ 个环的方案数。
### 递推式子。
边界 $\begin{bmatrix}n\\0\end{bmatrix} = [n=0]$。
$\begin{bmatrix}n\\m\end{bmatrix}=\begin{bmatrix}n-1\\m-1\end{bmatrix} + (n-1)\begin{bmatrix}n-1\\m\end{bmatrix}$
$\begin{bmatrix}n-1\\m-1\end{bmatrix}$ 是因为可以新建一个环。
$(n-1)\begin{bmatrix}n-1\\m\end{bmatrix}$ 是因为可以放在 $n-1$ 个元素每个元素的后边。
那么式子显然成立。
### 性质。
$\sum_{i}^{n} \begin{bmatrix}n\\i\end{bmatrix} = n!$
证明:对于一个排列 $p$,$i$ 向 $p_i$ 连边,和构成的环是一一对应的,那么就是 $n!$。
$x^{\underline{n}} = \sum_{i}^{n}\begin{bmatrix}n\\i\end{bmatrix} (-1)^{n-i}x^i$。
证明:尝试归纳法证明这个。
$x^{\underline{n+1}} = (x-n)x^{\underline{n}}$。
$=(x-n)(\sum_{i}^{n}\begin{bmatrix}n\\i\end{bmatrix} (-1)^{n-i}x^i)$。
$=x(\sum_{i}^{n}\begin{bmatrix}n\\i\end{bmatrix} (-1)^{n-i}x^i) - n(\sum_{i}^{n}\begin{bmatrix}n\\i\end{bmatrix} (-1)^{n-i}x^i)$。
$=\sum_{i}^{n}\begin{bmatrix}n\\i\end{bmatrix} (-1)^{n-i}x^{i+1} + n(\sum_{i}^{n}\begin{bmatrix}n\\i\end{bmatrix} (-1)^{n-i+1}x^i)$。
$=\sum_{i=1}^{n+1}\begin{bmatrix}n\\i-1\end{bmatrix} (-1)^{n-i+1}x^{i} + n(\sum_{i=0}^{n+1}\begin{bmatrix}n\\i\end{bmatrix} (-1)^{n-i+1}x^i)$。
$=\sum_{i=1}^{n+1}(\begin{bmatrix}n\\i-1\end{bmatrix} + n\begin{bmatrix}n\\i\end{bmatrix}) (-1)^{n-i+1}x^i$。
$\because \begin{bmatrix}n\\m\end{bmatrix}=\begin{bmatrix}n-1\\m-1\end{bmatrix} + (n-1)\begin{bmatrix}n-1\\m\end{bmatrix}$
$=\sum_{i=1}^{n+1}\begin{bmatrix}n\\i\end{bmatrix} (-1)^{(n+1)-i}x^i$。
$\because \begin{bmatrix}n+1\\0\end{bmatrix}=0$。
那么结论仍成立。
### 求第一类斯特林数。
$\sum_{i=0}^{n}\begin{bmatrix}n\\i\end{bmatrix} x^i = \prod_{i=0}^{n-1}(x+i)$。
$F(x)^n = \prod^{n-1} (x+i)$。
$F(x)^{2n} = \prod^{2n-1} (x+i)$。
$F(x)^{2n} = F(x)^n \times F(x+n)^n$。
$F(x+n)^n = \sum_{i=0}^{n}a_i(x+n)^i$。
$= \sum_{i=0}^n a_i \sum_{j=0}^{i} \binom{i}{j}n^{i-j}x^{j}$。
$= \sum_{i=0}^{n}(\sum_{j=i}^n \binom{j}{i}n^{j-i}a_j) x^i$。
$= \sum_{i=0}^{n}(i!)^{-1} x^i (\sum_{j=i}^{n})$
(没填完,以后再说)
## 第二类斯特林数。
$\begin{Bmatrix}n\\m\end{Bmatrix}$ 表示第二类斯特林数。 其组合意义是 $n$ 个元素划分成 $m$ 个非空子集的方案数。
# 字符串。
## 哈希。
考虑模数,尽量双哈希。
出错率应该是 $lcm(mod_1,mod_2)$。
**upd:修一个坑,这个地方不是 lcm 就行,应该要开一个根号,根据生日悖论那套理论。**
但是可以卡。感觉没必要代码。
是不是大家都会啊?我觉得你不会我也很难教你。
## kmp。
每次跟递推一样的算出来 $fail_i$
考虑 $fail_i$ 一定是 $[1,i]$ 的 $border$。
那么我们在 while 循环的时候其实就是在找一个相同前缀的并转移。
这个 $fail_i$ 其实就是 $[1,i]$ 的 **border**。
所以想要求 $border^n$ 大概就是在 $fail$ 树上倍增。
## manacher。
manacher 的话就是一个裸暴力吧?
想法大概就是我们求出来了 **abab**aba 的部分。
然后已经扩展完了对吧。因为 3 和 5 位置对称,又因为现在右端点最长的是以 4 为中心,7 为右端点的。因为它是回文的,所以 3 和 5 本质相同,但是**并不确定** 5 这个位置会不会向外扩展,所以只能先取一个自己知道的范围,但是我不会证明复杂度,感觉是对的,暂且认为是暴力吧。
求所有回文串的个数是 $\sum\frac{p_i}{2}$。
manacher 似乎可以用多个 $\log$ 的 哈希 代替。感觉也可以直接回文树吧。
## exkmp。
叫 exkmp 但是感觉和 kmp 没啥关系。
~~所以还是叫 Z 算法吧。~~
```cpp
const int maxn = 2e7 + 72;
int main() {
static char s[maxn], t[maxn];
static int n, m;
auto getZ = [&](char*s, int len) {
std::vector <int> Z(len + 1, 0); Z[1] = len;
for(register int i = 2, l = 0, r = 0; i <= len; i++) {
if(i <= r)
Z[i] = std::min(Z[i - l + 1], r - i + 1);
while(i + Z[i] <= len && s[i + Z[i]] == s[1 + Z[i]]) ++Z[i];
if(i + Z[i] - 1 > r)
l = i, r = i + Z[i] - 1;
}
return Z;
};
auto getP = [&](std::vector <int> Z) {
std::vector <int> P(n + 1, 0);
for(register int i = 1, l = 0, r = 0; i <= n; i++) {
if(i <= r)
P[i] = std::min(Z[i - l + 1], r - i + 1);
while(i + P[i] <= n && s[i + P[i]] == t[1 + P[i]]) ++P[i];
if(i + P[i] - 1 > r)
l = i, r = i + P[i] - 1;
}
return P;
};
in.reads(s + 1), in.reads(t + 1);
n = strlen(s + 1), m = strlen(t + 1);
std::vector <int> Z, P;
Z = getZ(t, m);
P = getP(Z);
long long ans1 = 0, ans2 = 0;
for(register int i = 1; i <= m; i++) ans1 ^= 1ll * i * (Z[i] + 1);
for(register int i = 1; i <= n; i++) ans2 ^= 1ll * i * (P[i] + 1);
printf("%lld\n%lld\n", ans1, ans2);
return 0;
}
```
代码先扔在这里(bushi)
### 例题
[CF126B题解](https://www.luogu.com.cn/blog/Isaunoya/solution-cf126b)
[CF1313E题解](https://www.luogu.com.cn/blog/Isaunoya/solution-cf1313e)
[CF432D without solution](https://www.luogu.com.cn/problem/CF432D)
## SA。
先假设给你一个串 ababababa 后缀排序对吧。
然后他会变成 **12121212121**。
发现不行,而且我们现在知道第一轮也就是 $k=2^0$ 的排序结果了。
于是我们就可以求出来 $k = 2^1$ 的排序结果,$1$ 和 $2$ 可以 merge 一下,$2$ 和 $1$ 同理。
如果后边是空的,那么默认为 0。
所以这个其实是 **12121212121**0 -> **2323232321**
然后反复 $i$ 和 $i + k$ 组合基数排序就好了,$k$ 倍增即可。
仔细一点的话就是说:
我们先设 $sa_i$ 为 rk 为 $i$ 的位置,$rk_i$ 为 $i$ 的位置的排名。
其实后缀数组可以拿来倍增的原因是因为。
你在上一轮排序当中,排序了 $i$ 和 $i+k$ 的相对位置,然后两段开头可以合起来成为 $k' = 2k$ 的一段,并且排名有依据。
注意开始排序就好了。我们在最开始的时候,可以求出来 $i$ 的位置,就是按 $a_i$(即字符串ASCII)来排序。
倒着排的,因为越后面的越短,后面是空的话,就选短的那个。
然后我们第二个关键字,即 $i+k+1$ 的地方,这里用 $y_i$ 表示第 $i$ 名,空串先丢进去,然后我们发现如果$sa_i$大于$k$也给他丢进去,枚举 $i$ 这样就可以保证有序。
是因为你每一轮都求出来了 $sa_i$ 的相对排名。
然后 $x$ 呢,最开始是 $a_i$,我们可以经过一轮排序,把 $x$ 丢到 $y$ 里,因为此时你的第二关键字是没有用的。
我们发现,$sa_i$ 是 rk 为 $i$ 的位置,然后你在这个 $x_{sa_i}$ 上操作就可以得到 $x_{i}$ 所谓的排名了。
[这里](https://www.cnblogs.com/Isaunoya/p/12505026.html)
lcp 的求法是求 $rk_i$ 表示 $i$ 这个位置的排名,然后相邻的来找就行了。
$lcp(i, j)$ 的求法就是 st 表 $O(1)$
SAM st 表 fail 树上处理 lca 也是可以做到 $O(1)$ 查询的。
**本质不同子串个数**
SA 上通过 lcp 来搞搞吧。
SAM fail树上 $\sum len_i - len_{fa_i}$
```cpp
int n ;
const int maxn = 1e6 + 5 ;
char a[maxn] ;
int sa[maxn] ;
void buildsa() {
static int x[maxn] , y[maxn] , buc[maxn] ;
int M = 122 ;
for(int i = 1 ; i <= n ; i ++)
++ buc[x[i] = a[i]] ;
for(int i = 1 ; i <= M ; i ++)
buc[i] += buc[i - 1] ;
for(int i = n ; i ; i --)
sa[buc[x[i]] --] = i ;
for(int k = 1 ; k <= n ; k <<= 1) {
int p = 0 ;
for(int i = n - k + 1 ; i <= n ; i ++)
y[++ p] = i ;
for(int i = 1 ; i <= n ; i ++)
if(sa[i] > k) y[++ p] = sa[i] - k ;
for(int i = 1 ; i <= M ; i ++)
buc[i] = 0 ;
for(int i = 1 ; i <= n ; i ++)
++ buc[x[y[i]]] ;
for(int i = 1 ; i <= M ; i ++)
buc[i] += buc[i - 1] ;
for(int i = n ; i ; i --)
sa[buc[x[y[i]]] --] = y[i] ;
swap(x , y) ;
x[sa[1]] = p = 1 ;
for(int i = 2 ; i <= n ; i ++)
x[sa[i]] = (y[sa[i]] == y[sa[i - 1]] && y[sa[i] + k] == y[sa[i - 1] + k]) ? p : ++ p ;
if(p >= n) break;
M = p ;
}
}
```
## AC 自动机。
~~突然想起来还有这么一个东西我没有写过学习笔记的~~
AC 自动机的三个板子
- [P5357 【模板】AC自动机(二次加强版)](https://www.luogu.com.cn/problem/P5357)
- [P3808 【模板】AC自动机(简单版)](https://www.luogu.com.cn/problem/P3808)
- [P3796 【模板】AC自动机(加强版)](https://www.luogu.com.cn/problem/P3796)
首先你需要会字典树,最好会 kmp ,不会也无所谓。
AC 自动机我个人觉得和 $kmp$ 没啥联系,只和字典树有关系2333,因为 AC 自动机是`基于字典树上的bfs`建造出来的。
如果给你几个串,你 $kmp$ 的复杂度显然不可以接受,所以就需要我们的 AC 自动机了。
我个人习惯从 $cnt = 1$ 开始,即字典树的 $root$ 为 $1$,以及 $ch_{u,i}$ 来表示字典树的节点,**我更倾向于把字典树的一个节点当做是字符串,因为从根节点顺次下来确实是一个字符串。**
首先你要明白 $fail_i$ 和 $i$ 的关系是 $fail_i$ 是 $i$ 的子串,以及,当你构造完 AC 自动机之后,$ch_{u,i}$ **不一定是原字典树的样子**,就是说会相对于字典树的结构变化,比如说跨越层,但是并不难理解,其实就是为了 $fail$ 的转移。
如果实际需要,比如说 [这一题](https://www.cnblogs.com/Isaunoya/p/12384231.html),你就可以先复制原有节点,然后建 AC 自动机。
$fail_i -> i$ 连边会成为一棵树,而树内查询之类的可以用树状数组等数据结构维护,其中有一条重要性质:$i$ 的子树内所包含的节点,都是包含 $i$ 这个子串的(~~我上面说过我喜欢把节点作为字符串了~~)
~~总感觉不是很好讲,那我来画图吧。~~ 举例子是最好的办法。 ~~为了方便画图,我给出两个字符串 "ab" "bab"~~
**图1: 建成一颗字典树**
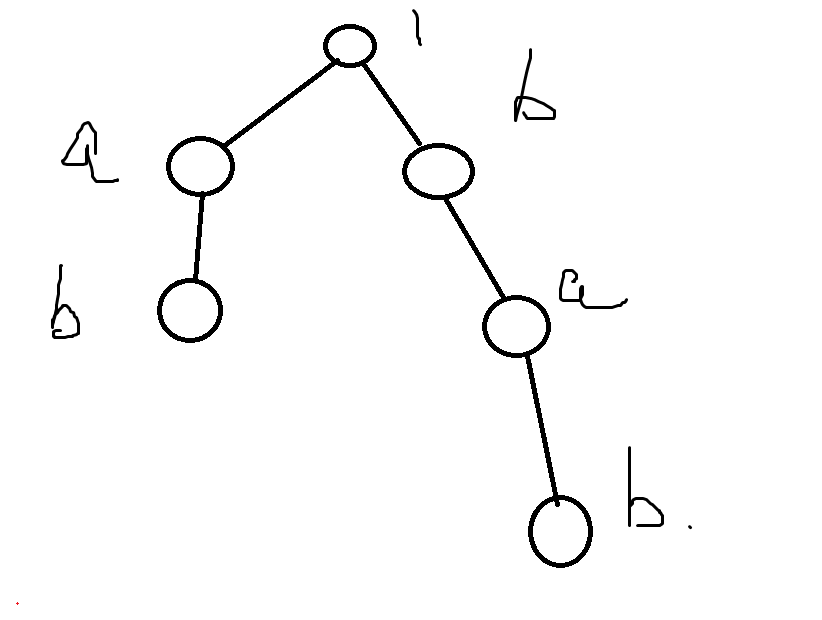
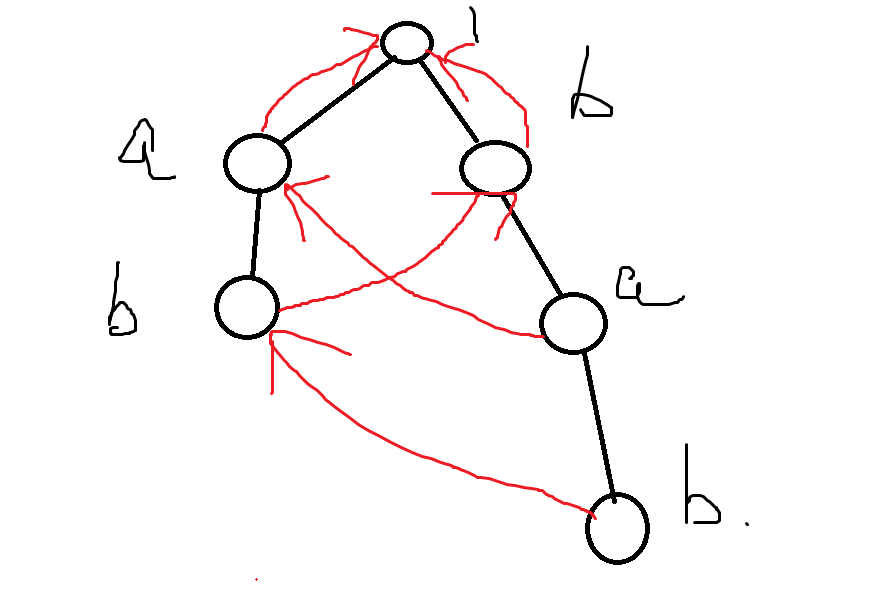
**图2:建一个 AC 自动机**
如何构建呢?我把构建好的放出来。在这个图里 $i$ 指向 $fail_i$
举个栗子,我们先找到 "bab" 对应的节点 $i$ ,然后你发现 $fail_i$ 指向的节点所对应的字符串是 "ab",以及找到其他的 $fail_i$ 和 $i$ 的关系都是这样。
即 $fail_i$ 所对应的字符串是 $i$ 所对应字符串的子串并且是 $i$ 的后缀。
如果我是 "abca" "babd" 呢,原有的 AC 自动机不用做任何变化,接着画就好了。
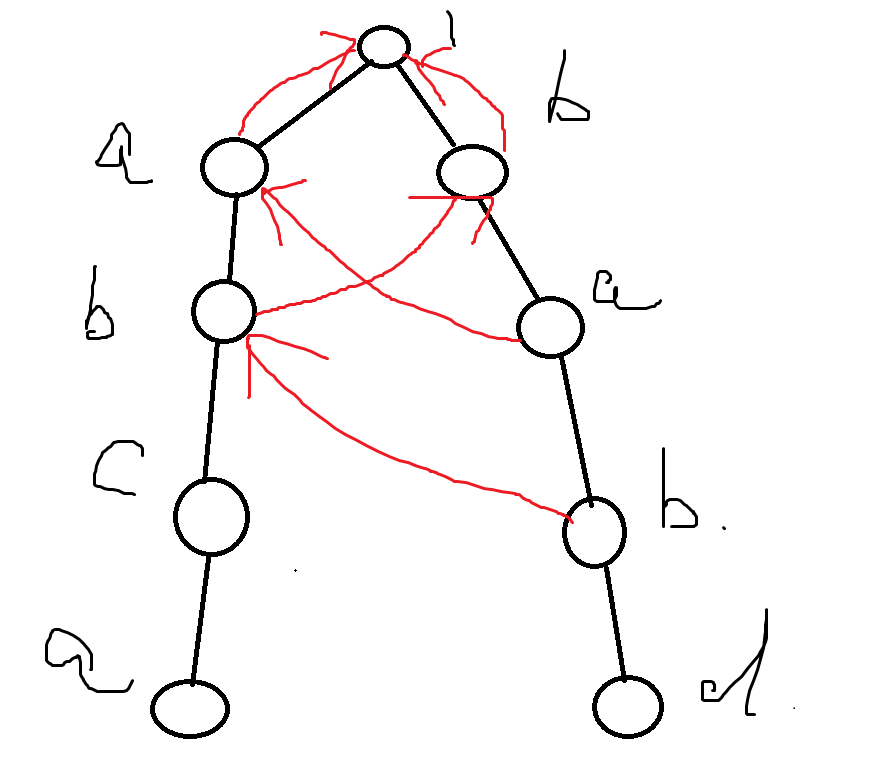
诶,然后你发现你的 "abc" 没办法找到一个 $fail_i$,没关系,那就连到根节点,然后你会发现你的 "babd"也找不到一个相同后缀的子串,没关系,那也丢给根节点。
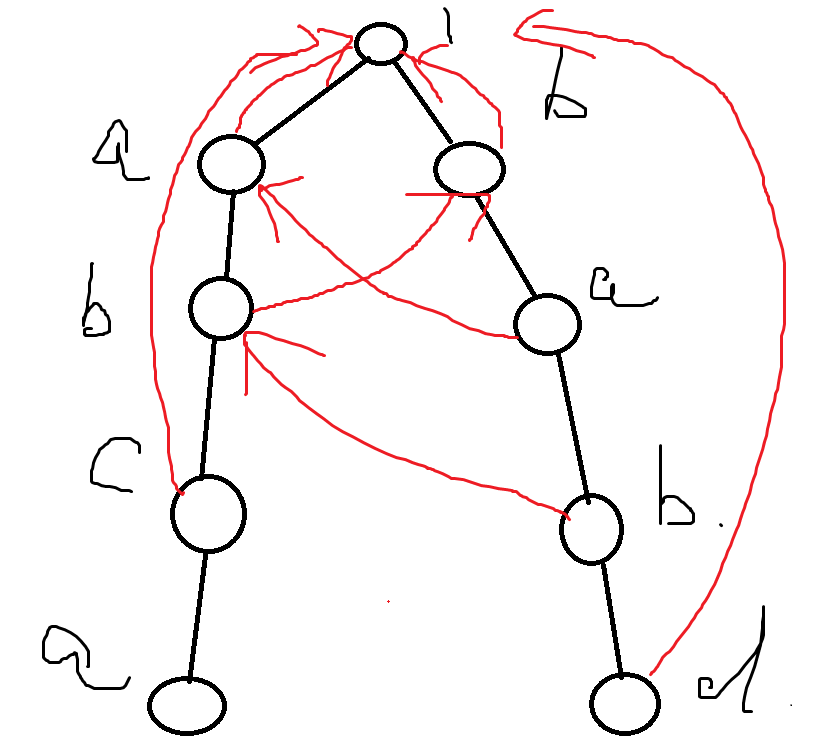
~~然后画成这个 b 样子了~~
然后你发现你的 "abca" 只能找到一个短短的相同后缀 "a",那就连上,所以 AC 自动机就建好了。
我们尝试画一个 AC 自动机的 $fail$ 树。(其实就是把 $fail_i$ 和 $i$ 连起来嘛…)
我们就很自然的发现了 AC 自动机 $fail$ 树的特点了(虽然我前面提到过)
代码
```cpp
std ::queue<int> q;
for (int i = 0; i < 26; i++)
if (ch[1][i])
fail[ch[1][i]] = 1, q.push(ch[1][i]);
else
ch[1][i] = 1;
while (!q.empty()) {
int u = q.front();
q.pop();
for (int i = 0; i < 26; i++)
if (ch[u][i])
fail[ch[u][i]] = ch[fail[u]][i], q.push(ch[u][i]);
else
ch[u][i] = ch[fail[u]][i];
}
for (int i = 2; i <= cnt; i++) g[fail[i]].pb(i);
```
然后我们来看例题 [P3808 【模板】AC自动机(简单版)](https://www.luogu.com.cn/problem/P3808)
给定n个模式串和1个文本串,求有多少个模式串在文本串里出现过。
我们直接对 $n$ 个模式串建 AC 自动机,然后在上面跑就好了,一直跳 $fail$,查询以当前结尾的串有多少个子串的 $end$ 节点是这个,用 $ed_i$ 表示这个出现次数,不能反复计算,所以计算过的就弄成 $-1$。
也不会忽略上面的贡献,因为如果 $ed_i == -1$,那么 $fail_i,fail_{fail_i}$ 也一定是 $-1$。
```cpp
int find(string s) {
int ans = 0 , p = 0 ;
for(char c : s) {
int x = c - 'a' ;
p = ac[p].son[x] ;
for(int j = p ; j && ac[j].end != -1 ; j = ac[j].fail)
ans += ac[j].end , ac[j].end = -1 ;
}
return ans ;
}
```
- [P3796 【模板】AC自动机(加强版)](https://www.luogu.com.cn/problem/P3796)
你需要找出哪些模式串在文本串 $T$ 中出现的次数最多。
对末尾节点标记为 $num_i = j$ 表示 $i$ 节点表示的字符串是第几个串。
我们考虑他后缀包含的子串,直接暴力跳 $fail$,一路加过去就好了。
这样就没了qwq。
```cpp
void query(string s){
int now=0;
for(int i=0;i<s.size();i++){
now=ch[now][s[i]-'a'];
for(int j=now;j;j=fail[j])ans[num[j]]++;
}
}
```
# 期望。
[根据期望的线性性,我们可以做这题](https://www.cnblogs.com/Isaunoya/p/13502732.html)
# 单调性。
看 FlashHu。