【题解】【LGR-(-15) 】SCP 2022 第一轮(初赛 S 组)模拟
wsyhb
·
·
个人记录
前言
(2022.8.28)
NOI 已经结束了,快来做初赛题吧~(大雾)
历经将近一周的打磨,这篇题解终于公开了。
最初天真地以为当天就能写完……
(2022.8.23)
原本计划着今天上午准时参加的,没想到竟完全忘了……
中午和下午花了点时间做了一遍,然后对了答案,只有 89 分。
当然实际参赛的话分会更低,因为比赛时长也就 2 h,而我做了……
话说回来我为什么错了整整四道单选啊!!!(抓狂)
和去年的那篇题解不同,这篇题解更多的是一些吐槽,实质性内容很少。
UPD(2022.8.28):写完发现内容还是挺丰厚的。
想要复习初赛的可以去这里看看,文章包含去年初赛模拟的解析。
写了也是白写,反正肯定不会有人仔细去读的。
初赛越来越难,我该怎么办……这模拟赛给我一种连 CSP 第一轮都过不了的不祥预感……
话说你谷把初赛模拟出这么难是不是想骗大家去报初赛课程啊?
最后祝各位 CSP2022 第一轮 RP++!
正文
比赛地址:【LGR-(-15) 】SCP 2022 第一轮(初赛 S 组)模拟。
题面及答案下载地址:题面;答案。
一、单项选择题
由于是 8 进制,所以最好先转 2 进制,再转其它进制。
由于是单选题,所以根本没有必要去计算 B 选项。(应该不会有人想去算 5 进制吧)
注意问的是“值为假的”。
------------

本质上是把斐波那契数拆分成了若干个 $1$,所以时间复杂度为 $O(\mathit{Fib}_n)$。
众所周知,斐波那契数列增长速度呈指数级,故会超时。
递归层数为 $O(n)$,不会栈溢出。
------------

从左到右扫描后缀表达式,将参与运算的元素加入一个栈,每来一个运算符就将栈顶的两个元素取出,进行相应运算并将结果加入栈中,即可得到中缀表达式(平常所写的表达式)。
虽然这里没有考察,但需注意更靠近栈顶的那一个元素应放在运算符右侧。
------------

~~一年以后还是不会做系列。~~
先计算有多少帧图像:$4 \times 60 \times 10=2400$。
然后计算每帧图像的大小:$2048 \times 1152 \times 32=75497472$。
由于没有压缩,所以乘起来并换算单位即可。
注意单位是从位到 GiB,所以要除以 $8 \times 1024 \times 1024 \times 1024$。
------------
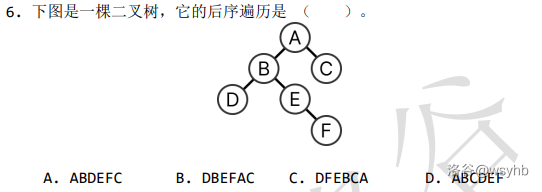
二叉树的先/中/后序遍历指的是根相较于两个儿子的遍历顺序。(左儿子的遍历总是在右儿子以前)
------------

五个点 $\binom{5}{2}=10$ 条边(亦可穷举),每条边要或不要,故答案为 $2^{10}$。
------------

每个选项模拟一下即可。
------------

点数排序相当于只关心每种点数的出现次数。
设点数 $i$ 的出现次数为 $c_i$,则 $c_1+c_2+\cdots+c_6=k$。
将非负整数解转化为正整数解:令 $d_i=c_i+1$,则 $d_1+d_2+\cdots+d_6=k+6$。
由隔板法知答案为 $C_{(k+6)-1}^{6-1}=C_{(k+6)-1}^{k}$。
------------

放回:每次取球独立,每一次的期望均为 $\dfrac{1+2+3+4+5+6}{6}=3.5$,所以答案为 $10.5$。
不放回:消序后相当于 $6$ 个球选 $3$ 个球,每个球被选的方案数均为 $\binom{5}{2}=10$(剩余球中选两个),总方案数为 $\binom{6}{3}=20$,所以答案为 $\dfrac{10 \times (1+2+3+4+5+6)}{20}=10.5$。
事实上,依据高中数学教材,$N$ 个元素,做 $n$ 次不放回随机抽样,每个元素被抽到的概率均为 $\dfrac{n}{N}$,由此可以直接得到答案。(当然本质一致)
------------
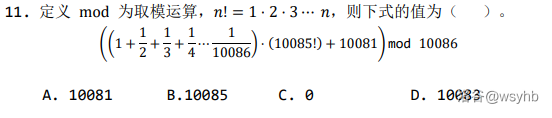
诈骗题。
$10086=2 \times 3 \times 1681$,而 $10085!$ 中 $2,3,1681$ 的倍数足够多,所以除以一个 $\le 10086$ 的正整数后也肯定是 $10086$ 的倍数,故答案为 $10081$。
------------

~~实名举报出题人暗示选手作弊!!!~~
记 $x=n$ 时 `ans` 的值为 $f_n$,递推计算 $f$ 即可。
我自己做的时候因为最后没有加一而功亏一篑……
------------

感觉这道题目有点题意不清啊——最优的分治方式……
题目期望的是按照建线段树的方式合并区间信息,以做到 $O(n)$ 的时间复杂度。
~~这谁想得到啊,优化复杂度的题目有意思吗。~~
------------

使用[主定理](https://oi-wiki.org/basic/complexity/#%E4%B8%BB%E5%AE%9A%E7%90%86-master-theorem)得 $T(n)=\Theta(n^2)$。
($a=9$,$b=3$,$f(n)=n$,故为第一种情况)
当然如果你像我一样记不得这东西,你也可以暴力展开:
$$\begin{aligned}
T(n)&=9(9T(\frac{n}{9})+\frac{n}{3})+n\\
&=9(9(9T(\frac{n}{27})+\frac{n}{9})+\frac{n}{3})+n\\
&=9^3T(\frac{n}{3^3})+9n+3n+n\\
&=\cdots\\
&=9^kT(\frac{n}{3^k})+\sum_{i=0}^{k-1}3^k \cdot n
\end{aligned}$$
取 $k=\log_3{n}$ 得 $T(n)=\Theta(n^2)$。
------------
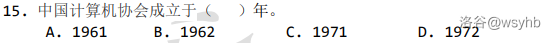
赛时我猜了一个 D。~~果然错了。~~
一打开 [CCF 官网](https://www.ccf.org.cn/),你就会看到这样一个界面:

故选 B。
初赛模拟出题组还是挺有心的,60 周年纪念所以就考了个这个。
不过既然此处出过了,那 CSP2022 第一轮应该就不会考这个了。
### 二、阅读程序
1.
``` cpp
#include <cstdio>
#include <cstring>
const int maxn = 1003;
int type, n, m;
char s[maxn], t[maxn];
int main() {
scanf("%d %s %s", &type, t, s);
n = strlen(s); m = strlen(t);
if (type < 2) {
for (int i = 0; i < m; ++i) s[i] = t[i];
} else if (type == 2) {
strcpy(s, t);
// 提示:如果此时调用 printf("%s\n", s),则本次输出结果为整个 t 字符串和换行,没有其他字符。
} else {
for (int i = 0; i < m; i += 4) {
unsigned int code = 0, pos = i;
for (int j = 1; pos < i+4; j*=100, ++pos) {
if (pos == m) break;
code += t[pos] * j;
}
pos = i;
while (code != 0) {
s[pos++] = code % 100;
code /= 100;
}
}
}
for (int i = 0; i < n; ++i) printf("%c", s[i]);
printf("\n");
}
```

#### 代码解读
乍一看三种类型都是把字符串 $t$ 复制到字符串 $s$,但其实暗藏玄机——
- 对于 $\mathit{type}=1$,用字符串 $t$ 覆盖 $s$ 的前缀,保留 $s$ 比 $t$ 长的部分。
- 对于 $\mathit{type}=2$,用字符串 $t$ 覆盖整个字符串 $s$。
- 对于 $\mathit{type}=3$,期望效果与 $\mathit{type}=1$ 相同,但实际上会在 $t$ 包含 ASCII 码 $\ge 100$ 的字符时出错。(大写字母的 ASCII 码 $<100$;而小写字母 $\texttt{a}$ 的 ASCII 码为 $97$)
#### 题目解析
1. 错。若将 `type<2` 改为 `type!=2`,则 $\mathit{type}=3$ 时也会执行 $\mathit{type}=1$ 的操作。
1. 对。理由见代码解读。
1. 错。理由见代码解读。
1. 对。该问题相当于“是否一定有 $\mathit{code}>0$”;由于外层 `for` 循环的限制为 `i<m`,所以内层 `for` 循环是一定对 `code` 进行了修改的,又大小写字母的 ASCII 码是不超过 $122$ 的正整数,故 `code` 不可能是 $2^{64}$ 的倍数(即 `code` 不为 $0$)。
1. 选 B。函数 `strlen()` 与 `string` 类型的成员函数 `size()` 不同,会遍历整个字符串以计算长度,时间复杂度为线性,因此该 `for` 循环的时间复杂度为 $O(m^2)$(另外还需算上输入输出的复杂度)。
1. 选 C。字符 $\texttt{f}$、$\texttt{g}$ 和 $\texttt{h}$ 的 ASCII 码依次为 $100,101,102$,因此实际效果与 $\mathit{type}=1$ 不同。
----
2.
``` cpp
#include <iostream>
using namespace std;
const int INF = 1000000000;
#define Front 0
#define Back 1
#define Left 2
#define Right 3
#define Up 4
#define Down 5
int w[6], a[1003][1003];
const int way1[] = {Up, Right, Down, Left};
const int way2[] = {Up, Front, Down, Back};
const int way3[] = {Left, Front, Right, Back};
int get_max(int &a, int b) {
return a = max(a, b);
}
int right_rotate(int &u) {
for (int i = 0; i < 4; ++ i)
if (u == way1[i])
return u = way1[(i + 1) % 4];
return u;
}
int front_rotate(int &u) {
for (int i = 0; i < 4; ++ i)
if (u == way2[i])
return u = way2[(i + 1) % 4];
return u;
}
const int anchorX = Up;
const int anchorY = Front;
const int anchorZ = Right;
int find_down(int u, int v) {
if (u == Down || u == Up) return anchorX^(u == Up);
if (v == Down || v == Up) return anchorY^(v == Up);
for (int i = 0; i < 4; ++ i)
if (u == way3[i])
return anchorZ ^ (v == way3[(i + 1) % 4]);
return -1;
}
int n, m, dp[1003][1003][6][6];
int main() {
cin >> n >> m;
for (int i = 0; i < n; ++ i)
for (int j = 0; j < m; ++ j)
cin >> a[i][j];
for (int i = 0; i < 6; ++ i)
cin >> w[i];
for (int i = 0; i < n; ++ i)
for (int j = 0; j < m; ++ j)
for (int a = 0; a < 6; ++ a)
for (int b = 0; b < 6; ++ b)
dp[i][j][a][b] = -INF;
dp[0][0][anchorX][anchorY] = a[0][0] * w[Down];
for (int i = 0; i < n; ++ i)
for (int j = 0; j < m; ++ j)
for (int p = 0; p < 6; ++ p)
for (int q = 0; q < 6; ++ q)
if (dp[i][j][p][q] != -INF) {
int x = dp[i][j][p][q];
int u1 = p, v1 = q;
right_rotate(u1);
right_rotate(v1);
get_max(dp[i][j + 1][u1][v1],
x + w[find_down(u1, v1)] * a[i][j + 1]);
int u2 = p, v2 = q;
front_rotate(u2);
front_rotate(v2);
get_max(dp[i + 1][j][u2][v2],
x + w[find_down(u2, v2)] * a[i + 1][j]);
}
int ans = -INF;
for (int p = 0; p < 6; ++ p)
for (int q = 0; q < 6; ++ q)
ans = max(ans, dp[n - 1][m - 1][p][q]);
printf("%d\n", ans);
return 0;
}
```

#### 代码解读
~~这种鬼代码谁读得懂啊!~~
个人理解:代码读入了一个大小为 $n \times m$ 的数组 `a`,似乎是一个棋盘的权值分布。然后又读入了一个大小为 $6$ 的数组 `w`,似乎是各个方向的权值。然后从位置 $(0,0)$ 出发进行了一个 DP,每次只能向右或向下走,且 DP 值为经过位置的“棋盘上的权值 $\times$ 某个方向的权值”(方向根据实际情况确定,并非任意)之和的最大值,输出的是 $(n-1,m-1)$ 的 DP 值。方向的更新使用到了 `right_rotate()` 和 `front_rotate()` 这两个函数。
神级理解:(请先阅读[洛谷 P8488 题面](https://www.luogu.com.cn/problem/P8488))
- 当骰子的两个不互为对立面的面的朝向确定时,整个骰子的朝向确定,故 DP 状态的后两维记录了骰子某两个代表面的朝向(代码中依次为初始时朝上和朝前的面)。
- 函数 `right_rotate()` 和 `front_rotate()` 分别用于向右和向前翻骰子时朝向的更新。
- 函数 `find_down()` 的作用:根据代表面的朝向确定骰子当前朝下的一面。具体逻辑如下:($u$ 即代码中的 `u`,表示 `anchorX` 的朝向;$v$ 同理)
- 若 $u$ 为向下/向上,则向下的面为 `anchorX` 或 `anchorX^1`(即 `anchorX` 的对立面);$v$ 同理。
- 若 $u,v$ 均不为向上/向下,则 $u,v$ 为其余四个方向中不互为相反方向的两个方向。此时若 $u$ 逆时针旋转 $90\degree$ 可得到 $v$,则向下的面为 `anchorZ^1`,否则为 `anchorZ`。(若想象不出来,建议自己画个图)
#### 题目解析
1. 错。传入函数 `find_down()` 的参数显然是 $0$ 到 $5$ 之间的整数;若 $u=4,5$(对应代码中的 `Up` 和 `Down`),则该函数会在 `for` 循环开始前就返回;否则一定存在 $i \in [0,3]$ 使得 `way3[i]` 和 $u$ 相等,因此该函数在 `for` 循环退出前一定会返回。(P.S. 这是笔者最初从【个人理解】出发做出的分析,事实上如果理解了代码求解的东西是什么,则本题显然)
1. 错。时间复杂度显然为 $O(nmc^2)$,其中常数 $c=6$,表示方向的种类数。(事实上还有一个 $4 \times 4$ 的小常数)
1. 错。任选一个带入验证即可。
1. 选 D。`anchorX`,`anchorY` 和 `anchorZ` 需要满足如下位置关系: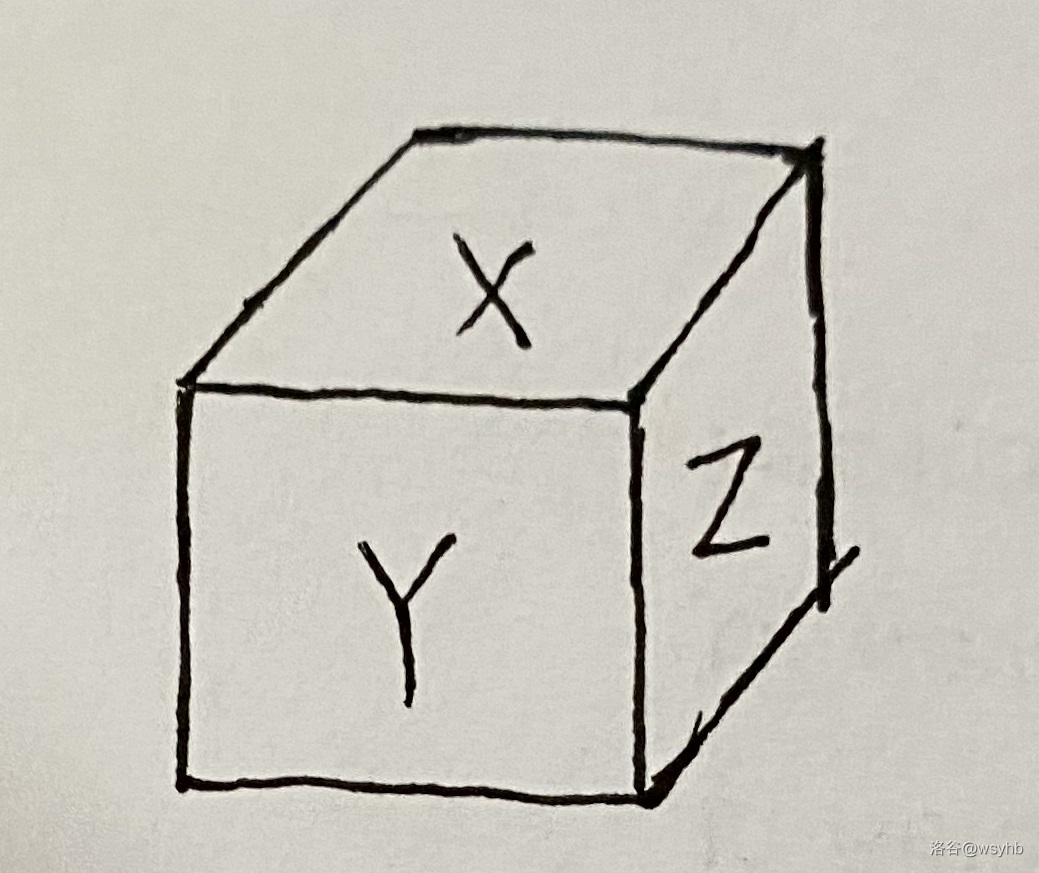
1. 选 B。由于 $w_0=w_1=\cdots=w_5=1$,故答案为 $(1,1)$ 到 $(n,m)$ 的路径的最大权值和,手玩即可。(DP 或人脑启发式搜索均可)
1. 选 A。可能的五条路径的权值和依次为:(骰子上的数在前,棋盘上的数在后)
- $6 \times 2+1 \times 5+4 \times 19+2 \times 19+3 \times 3+1 \times 5=145
- $6 \times 2+4 \times 8+1 \times 19+5 \times 19+2 \times 3+6 \times 5=194$
- $6 \times 2+4 \times 8+5 \times 15+1 \times 19+3 \times 3+2 \times 5=157$
- $6 \times 2+4 \times 8+5 \times 15+3 \times 3+1 \times 3+6 \times 5=161$
- $6 \times 2+4 \times 8+5 \times 15+3 \times 3+6 \times 10+1 \times 5=193$
P.S. 最好把骰子每一步的状态都在草稿纸上写清楚,不然很容易算错。
P.S. 即使你像我一样没读懂代码,第 1,2,3,5 题仍然是可做的。
闲话
即使没读懂也能猜对第 6 题,不是吗?
-
#include <bits/stdc++.h>
using namespace std;
const int MAXN = 309;
const int MAXM = 109;
const int MAXP = 100000;
typedef long long ll;
int n, m, seed,rt,btm,s[MAXM],Len,dfncnt,full_dist,P,t;
int lg[MAXN],dfn[MAXN],fa[MAXN],dep[MAXN], lson[MAXN];
vector <int> e[MAXN];
vector <int> L[MAXM],leaves;
int F[MAXM];
namespace LCA {
int st[24][MAXN];
int minNode(int x, int y) {
return dep[x] < dep[y] ? x : y;
}
void init() {
for (int i = 1; i <= n; ++i) st[0][dfn[i]]=fa[i];
for (int i = 1; i <= lg[n]; ++i)
for (int j = 1; j + (1 << i) - 1 <= n; ++j)
st[i][j] = minNode(st[i - 1][j], st[i - 1][j + (1 << (i - 1))]);
}
int lca(int u, int v) {
if (u == v) return u;
if ((u = dfn[u]) > (v = dfn[v])) swap(u, v);
int d = lg[v - u++];
return minNode(st[d][u], st[d][v - (1 << d) + 1]);
}
}
namespace Gen {
mt19937 rnd;
int pos[MAXN], deg[MAXN];
vector <pair<int, int>> edges;
void calc() {
for (int i = 1; i <= n - 2; ++i)
++deg[pos[i]];
set <int> ret;
ret.clear();
for (int i = 1; i <= n; ++i)
if (deg[i] == 1) ret.insert(i);
for (int i = 1; i <= n - 2; ++i) {
int npos = *ret.begin();
edges.push_back(make_pair(npos, pos[i]));
ret.erase(ret.begin());
--deg[pos[i]];
if (deg[pos[i]] == 1)
ret.insert(pos[i]);
}
edges.push_back(make_pair(*ret.begin(), n));
}
void build() {
for (auto i : edges) {
int u = i.first, v = i.second;
e[u].push_back(v);
e[v].push_back(u);
}
}
void generate(int seed) {
rnd.seed(seed);
edges.clear();
for (int i = 1; i <= n; ++i) deg[i] = 1;
for (int i = 1; i <= n - 2; ++i)
pos[i] = rnd() % n + 1;
calc();
build();
}
}
int dfs(int u, int _fa, int &bottom) {
dfn[u] = ++dfncnt;
if (e[u].size() == 1) leaves.push_back(u);
lson[u] = -1;
fa[u] = _fa;
dep[u] = dep[_fa] + 1;
int maxlen = 0, dson = u, temp;
for (int v: e[u])
if (v != _fa) {
int p = dfs(v,u,temp);
if (p > maxlen) maxlen = p, lson[u]=v, dson=temp;
}
bottom = dson;
return maxlen + 1;
}
#define dist(u, v) (dep[u]+dep[v]-2*dep[LCA::lca(u, v)])
int v[MAXP+9], prime[MAXP + 9], prime_cnt, vis[MAXP+9];
void prime_init(int n) {
prime_cnt = 0;
for (int i = 2; i <= n; ++i) {
if (!v[i]) prime[++prime_cnt] = v[i] = i;
for(int j=1; j <= prime_cnt && i*prime[j]<=n; ++j) {
if (v[i] < prime[j]) break;
v[i * prime[j]] = prime[j];
}
}
}
vector<int> answer, gline;
void solve() {
cin >> n >> m >> seed >> t;
lg[0] = lg[1] = 0;
for (int i = 2; i <= n; ++i) lg[i] = lg[i >> 1] + 1;
for (int i = 1; i <= n; ++i) e[i].clear();
leaves.clear();
if (!t) Gen::generate(seed);
else {
for (int i = 1, u, v; i < n; ++i) {
cin >> u >> v;
e[u].push_back(v);
e[v].push_back(u);
}
}
dep[0] = 0;
dfs(1, 0, rt);
dfncnt=0;
leaves.clear();
Len = dfs(rt, 0, btm);
LCA::init();
for (int k = rt; ~k; k = lson[k]) gline.push_back(k);
for (int i = 1, tmp; i <= m; ++i) {
{
cin >> s[i];
L[i].clear();
for(int j = 1; j <= s[i]; ++j) {
cin >> tmp;
L[i].push_back(tmp);
}
F[i] = dist(L[i].front(), L[i].back());
for (unsigned j = 0; j < L[i].size() - 1; ++j)
F[i] += dist(L[i][j], L[i][j + 1]);
int tmp = F[i] >> 1;
while (tmp > 1) vis[v[tmp]] = 1, tmp /= v[tmp];
}
full_dist = dist(leaves.front(), leaves.back());
for (unsigned i = 0; i < leaves.size() - 1; ++i)
full_dist += dist(leaves[i], leaves[i + 1]);
P = -100000;
for (int i = 2; i <= prime_cnt; ++i)
if (full_dist+2*Len<prime[i] * 2 && !vis[prime[i]]) {
P = prime[i] * 2;
break;
}
for (int i = 1; i <= m; ++i) {
F[i] >>= 1;
while (F[i]>1) vis[v[F[i]]] = 0, F[i] /= v[F[i]];
}
int left=P-full_dist;
int fcnt = left / (2 * (Len - 1));
answer = leaves;
while (fcnt--) answer.push_back(rt),
answer.push_back(btm), left -= 2 * (Len - 1);
if (left>>=1) answer.push_back(rt),
answer.push_back(gline[left]);
for (int qwq: answer) cout << qwq << " ";
cout << endl;
}
}
int main() {
prime_init(MAXP);
int T;
cin >> T;
while (T--) solve();
}
代码解读
`v` 数组记录的是每个数的最小质因数。
其余部分略。(很难找出直观的实际意义;除函数 `solve()` 以外都是板子;变量/函数名称具有很大的提示性)
#### 题目解析
1. 错。时间复杂度显然为 $O(1)$。
1. 对。证明可参考[随机树的直径:最遥远的彼方真的遥不可及吗?](https://zhuanlan.zhihu.com/p/398621082)(建议当结论记忆)。
1. 对。最坏情况下是以叶子为根把整棵树 dfs 遍历一遍,故 `full_dist` $\le 2(n-1)$。
1. 选 C。只有 $1$ 和 $5$ 是叶子,故排除 ABD。
1. 选 B。同样只需求得叶子有哪些。生成的树见下图: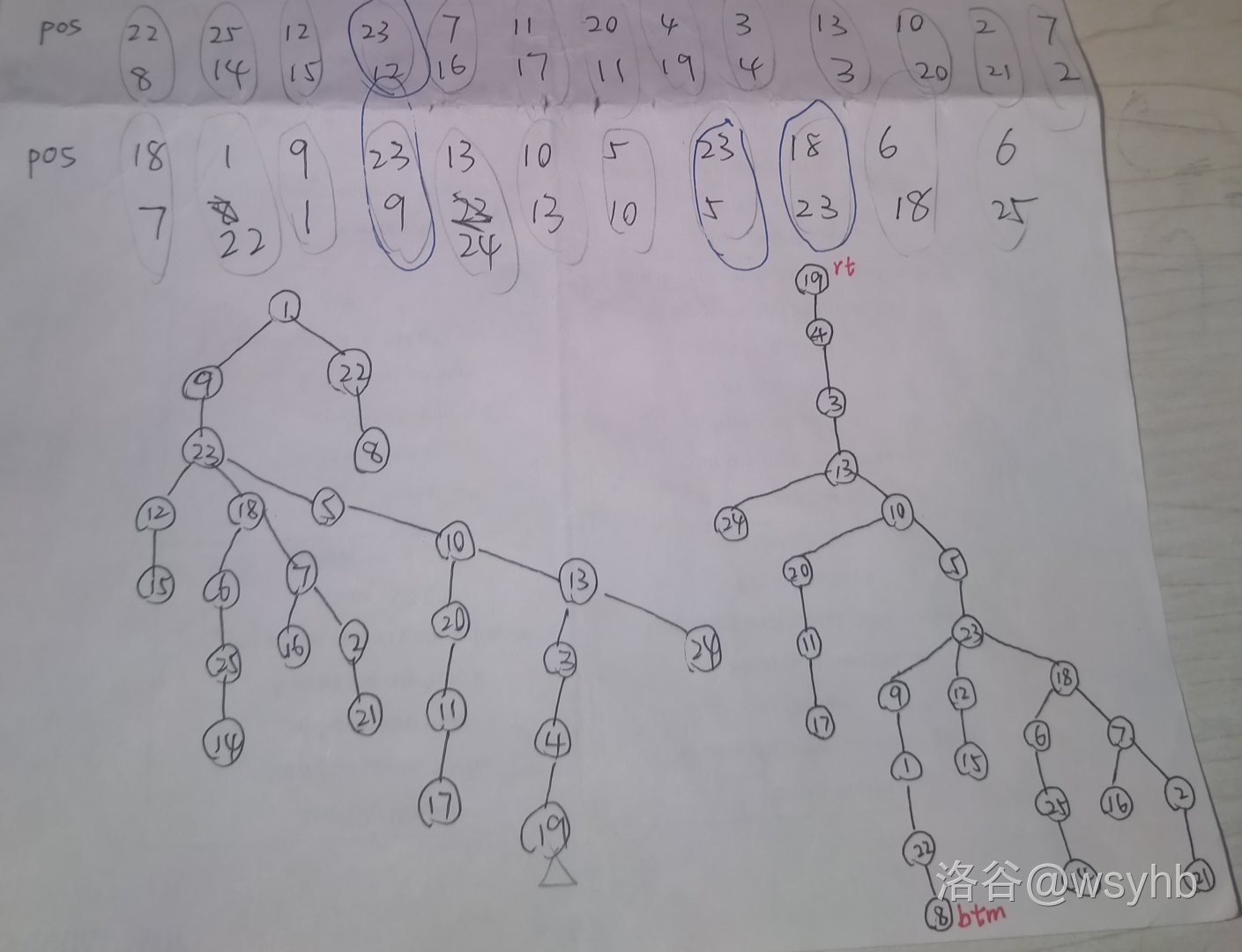
1. 选 D。由于质数不会太稀疏,所以 $P$ 约等于 `full_dist+2*Len`,进一步知 `fcnt` 为 $O(1)$。又 `answer` 中包含了树的所有叶子,所以序列长度理论上界为 $O(n)$。
#### 闲话
本来我一遍就把树建对了,但因为忘记 `leaves` 包含根,而让我以为我把树建错了,为此检查了两遍……
警钟长鸣。
------------
【无根树的 Prufer 序列】在 NOI 大纲里是 NOI 级的 9 级算法。
### 三、完善程序

``` cpp
#include <cstdio>
using namespace std;
const int maxn = 25;
const int aim = 17;
int n;
int a[maxn];
bool ans;
int getBit(const int s, int p) {
return ①;
}
int main() {
scanf("%d", &n);
for (②) scanf("%d", a + i);
for (int s=0, upperBound = ③; s <= upperBound; ++s) {
④;
for (int j = 0; j < n; ++j) if (getBit(s, j) == 1) {
sum += a[j];
} else {
⑤;
}
if (int(sum) == aim) {
ans = true;
break;
}
}
printf("%s\n", ans ? "Yes" : "No");
}
```

1. 选 A。即取出 $s$ 的二进制表示下的第 $p$ 位(数值为 $2^p$ 的那一位)。
1. 选 C。由后续代码中 `j` 的范围可得。
1. 选 D。全集对应的二进制数的每一位均为 $1$,即 $2^n-1$。
1. 选 B。$|\sum{a_i}|\le 2 \times 10^{10}$,所以需要开 `long long`(`unsigned long long` 也行)。
1. 选 C。即 `sum-=a[j]`。
事实上,**将 `sum` 强制转换为 `int` 类型是错误的**,可以被下面这组数据 Hack 掉:
(五个数的和为 $2^{32}+17$)
``` plain
5
1000000000 999999999 999999998 999999997 294967319
------
No
```
------------

``` cpp
#include <iostream>
#include <vector>
#include <algorithm>
typedef std::vector<int> Nodes;
struct RootedTree {
int size, root;
std::vector<Nodes> edges;
};
RootedTree read() {
RootedTree res;
std::cin >> res.size >> res.root;
res.edges.resize(res.size + 1);
for (int i = 1; i < res.size; ++ i) {
int u, v;
std::cin >> u >> v;
res.edges[u].push_back(v);
res.edges[v].push_back(u);
}
return res;
}
std::vector<Nodes> D; // 某个深度下的所有结点
std::vector<int> fa;
int dfs_depth(const RootedTree &tree, int now, int f, int
depth, int nodesDiff) {
if (①) // 1
D.push_back(Nodes());
int nowId = now + nodesDiff;
D[depth].push_back(nowId);
if (f != -1)
fa[nowId] = f + nodesDiff;
int maxDepth = 0;
for (int i = 0; i < tree.edges[now].size(); ++ i) {
int child = tree.edges[now][i];
if (②) { // 2
maxDepth = std::max(maxDepth,
dfs_depth(tree,child,now,depth+1,nodesDiff));
}
}
return maxDepth + 1;
}
typedef std::vector<int> Hash;
std::vector<Hash> hash;
bool cmp(const int x, const int y) {
return ③; // 3
}
bool check(const RootedTree &t1, const RootedTree &t2) {
if (t1.size != t2.size)
return false;
int size = t1.size;
D.clear();
fa.clear();
fa.resize(size * 2 + 1);
int dep1 = dfs_depth(t1, t1.root, -1, 0, 0);
int dep2 = dfs_depth(t2, t2.root, -1, 0, size);
if (dep1 != dep2)
return false;
hash.clear();
hash.resize(size * 2 + 1);
std::vector<int> rank(size * 2 + 1);
for (④) { // 4
for (int i = 0; i < D[h + 1].size(); ++ i) {
int node = D[h + 1][i];
hash[fa[node]].push_back(rank[node]);
}
std::sort(D[h].begin(), D[h].end(), cmp);
rank[D[h][0]] = 0;
for (int i = 1, cnt = 0; i < D[h].size(); ++ i) {
if (⑤) // 5
++ cnt;
rank[D[h][i]] = cnt;
}
}
return hash[t1.root] == hash[t2.root + size];
}
int main() {
RootedTree treeA, treeB;
treeA = read();
treeB = read();
bool isomorphism = check(treeA, treeB);
std::cout
<< (isomorphism ? "wow!" : "emm...")
<< std::endl;
return 0;
}
```

1. 选 D。`vector` 下标从 $0$ 开始,故若 `D.size()<=depth`,则 `D` 需要加长;又因为遍历到深度 $\mathit{depth}$ 时,深度 $0,1,\cdots,\mathit{depth}-1$ 均已被遍历过,故 D 项正确。
1. 选 B。`f`,`now` 以及 `edges` 中存储的元素均为每棵树的原编号。
1. 选 D。此处是按 `hash` 对节点进行排序的比较函数。
1. 选 C。用深度为 `h+1` 的节点更新深度为 `h` 的节点,而深度范围为 $0$ 到 `dep1-1`。(`dfs_depth` 返回的是树的层数;深度为 `dep1-1` 的叶子无差别,保持 `hash` 为空即可)
1. 选 A。此处是将 `hash` 离散化为 `rank`;也可以是 `>` 符号。
#### 闲话
这完善程序不比阅读程序阳间许多?