XXI Open Cup. Grand Prix of Korea

> 感谢 @jiangly 大神指导 **Link** : [CF gym](https://codeforces.com/gym/102759) Open Cup 好！ ## [DS] A ## [??] B Cactus Competition $\color{blue}\bigstar$ **题意** ： 给出两个序列 $A_{1\sim n},B_{1\sim m}$。 构造一个 $n\times m$ 的矩阵 $H$，其中 $H_{i,j}=A_i+B_j$。 从 $H_{1,s}$ 出发前往 $H_{n,t}$ ，其中只能经过权值非负的位置（包括起点和终点），且只能向右或向下行走。 求有多少组 $H_{s,1}\rightarrow H_{t,m}$ 是可达的。 $n,m\leq 2\times 10^5$ ，时限$\texttt{2s}$。 ------------ 先考虑如何判定 $H_{1,1}\rightarrow H_{n,m}$ 是否可达。 初看本题，没有什么好的切入点，尝试发掘一些简单的性质。 - 若 $\min\{A\}+\max\{B\}<0$ ，则说明有一行（$\min\{A\}$ 的那一行）全为负。 - 若 $\max\{A\}+\min\{B\}<0$ ，则说明有一列（$\min\{B\}$ 的那一列）全为负。 若满足上述两个条件之一，则说明 $H_{1,1}\rightarrow H_{n,m}$ 不可达。下面讨论它们不满足的情况。 - $\min\{A\}+\max\{B\}\geq 0$ ，则说明有一列（$\max \{B\}$ 的那一列）全非负。 - $\max\{A\}+\min\{B\}\geq 0$ ，则说明有一行（$\max \{A\}$ 的那一行）全非负。 我们发现了一个有趣的性质，在本题中，“存在一行全为负”否定后可以导出“存在一列全非负”。  画出这非负的一行一列，记为 $H_{i,\_},H_{\_,j}$ ，如图 $A$。 考虑构造一种方案，从左上角先来到 $H_{i,j}$ ，再前往 $H_{n,m}$。 若左上方黄色区域内存在一行**与**一列均为负，显然无解。否则，黄色区域内必然存在一行**或**一列非负。如图 $B$。 这样，就将左上角区域缩小了，不断重复，即可到达起点。类似地，也可以到达终点。 根据上面的观察，只需要排除下列四种阻断情况即可 ：  四种阻断均不存在 $\Longleftrightarrow$ 可以从 $H_{1,1}$ 到达 $H_{n,m}$。 接下来考虑如何计算答案。 对于全负的行，会将问题分成若干段子问题（也可以看做提供下界）。下面我们不再关心这类限制。 枚举 $s$ ，考虑有多少 $t$ 满足 $H_{s,1}\rightarrow H_{t,m}$ ： - $\max_{i\in[s,t]}A_i+\min\{B\}\geq 0$ 找出第一个 $i\geq s$ 使得 $A_i+\min\{B\}\geq 0$。则 $i\leq t$ 的都满足条件。 综上，蓝色和红色隔断为每个起点 $H_{s,1}$ 限制了一个终点的区间。 对于图中绿色和橙色的阻断，相当于直接除掉了一些起点和终点。 - 绿色，左上角阻断（橙色右下角阻断类似） 对于起点 $H_{s,1}$，若存在 $H_{x,y}$ 满足 $A_x+B_i<0\ (1\leq i\leq y)$ 且 $A_i+B_y<0\ (s\leq i\leq x)$ ，则将 $H_{s,1}$ 删除。 枚举 $x$ ，考虑所有 $H_{x,\_}$ 的贡献。 找到最小的 $j$ 使得 $A_x+B_j\geq 0$ （$B$ 从大到小排序后前缀编号 $\min$），则前缀 $A_x+B_{1\sim j-1}$ 都是负的。 为了尽量向上延伸，只需找到 $B_{1\sim j-1}$ 中最小的一个，记为 $B_y$。 然后找出一个最大的 $i\leq x$ 满足 $A_i+B_y\geq 0$ （单调栈 + 二分），则区间 $[i+1,x]$ 之间的起点都被删除。 先去除不合法的起点终点（可以用差分），然后若干次区间求和即可。 复杂度 $O\big((n+m)\log n\big)$。 注意不要把 $n,m$ 写反…… ```cpp #include<algorithm> #include<cstdio> #define MaxN 200500 using namespace std; int a[MaxN],b[MaxN],pl[MaxN],pr[MaxN],p2[MaxN],px[MaxN],p3[MaxN]; bool cmp(int A,int B){return b[A]<b[B];} int n,m,stk[MaxN],top,o1[MaxN],o2[MaxN],tl[MaxN],tr[MaxN]; int main() { scanf("%d%d",&n,&m); for (int i=1;i<=n;i++)scanf("%d",&a[i]); for (int i=1;i<=m;i++)scanf("%d",&b[p2[i]=i]); for (int i=1;i<=m;i++) pl[i]=(i==1||b[i]<b[pl[i-1]]) ? i : pl[i-1]; for (int i=m;i;i--) pr[i]=(i==m||b[i]<b[pr[i+1]]) ? i : pr[i+1]; sort(p2+1,p2+m+1,cmp); for (int i=1;i<=m;i++)px[i]=b[p2[i]]; p3[m+1]=m+1; for (int i=m;i;i--)p3[i]=min(p2[i],p3[i+1]); for (int x=1;x<=n;x++){ while(top&&a[x]>a[stk[top]])top--; stk[++top]=x; int j=p3[lower_bound(px+1,px+m+1,-a[x])-px]; if (j==1)continue; int y=pl[j-1]; if (a[stk[1]]+b[y]<0){o1[1]++;o1[x+1]--;continue;} int l=1,r=top,mid; while(l<r){ mid=(l+r+1)>>1; if (a[stk[mid]]+b[y]>=0)l=mid; else r=mid-1; }o1[stk[l]+1]++;o1[x+1]--; } for (int i=1;i<=n;i++)o1[i]+=o1[i-1]; for (int i=1;i<=n;i++)o1[i]=!o1[i]; p3[m+1]=0; for (int i=m;i;i--)p3[i]=max(p2[i],p3[i+1]); top=0; for (int x=n;x;x--){ while(top&&a[x]>a[stk[top]])top--; stk[++top]=x; int j=p3[lower_bound(px+1,px+m+1,-a[x])-px]; if (j==m)continue; int y=pr[j+1]; if (a[stk[1]]+b[y]<0){o2[x]++;continue;} int l=1,r=top,mid; while(l<r){ mid=(l+r+1)>>1; if (a[stk[mid]]+b[y]>=0)l=mid; else r=mid-1; }o2[x]++;o2[stk[l]]--; } for (int i=1;i<=n;i++)o2[i]+=o2[i-1]; for (int i=1;i<=n;i++)o2[i]=o2[i-1]+(!o2[i]); int minb=b[1],maxb=b[1]; for (int i=2;i<=m;i++) {minb=min(minb,b[i]);maxb=max(maxb,b[i]);} for (int s=n,t=n+1;s;s--){ if (a[s]+minb>=0)t=s; tl[s]=t; } for (int s=n,t=n;s;s--){ if (a[s]+maxb<0)t=s-1; tr[s]=t; } long long ans=0; for (int s=1;s<=n;s++) if (o1[s]&&tl[s]<=tr[s])ans+=o2[tr[s]]-o2[tl[s]-1]; printf("%lld",ans); return 0; } ``` ## [DP] C Economic One-way Roads **题意** ：给出一张 $n$ 个点的无向连通图。 将所有道路定向。每条道路定于两个方向都有各自的花费。 最终要使得定向后的图为强连通图，求最小花费。 $n\leq 18$ ，时限$\texttt{5s}$。 ------------ - **强连通图的耳分解** 有向图 $G=(V,E)$ 强连通当且仅当可以通过以下方法构造： 任选一个点 $s$，令 $S=\{s\}$。 重复以下过程直到 $S=V$。 任选两个点 $u,v\in S$。$u$ 和 $v$ 可以相同。 选择 $k\pod{k\ge 0}$ 个不同的点 $w_1,w_2,\ldots,w_k\not\in S$。 连接 $u\to w_1\to w_2\to\cdots\to w_k\to v$，并将 $w_1,w_2,\ldots ,w_k$ 加入 $S$。 其中，路径 $u\to w_1\to w_2\to\cdots\to w_k\to v$ 被称作“耳”。 考虑状压 $\rm DP$ ，记 $dp[S]$ 表示耳分解已经含有点集 $S$ ，$S$ 内部的最小花费。 然后枚举一条路径，路径上的边的费用是固定的，其余的边选择费用较小的方向。 然而这需要子集 $\rm DP$ ，复杂度为 $O\big(3^n{\rm poly}(n)\big)$ ，无法通过。 考虑类似轮廓线的思路，不要一次加入整条路径，而是逐个点加入。 记 $f[S][u][v]$ 表示已经加入了点集 $S$ ，还需要加入一条 $u\rightarrow v$ 的路径，最小的代价。转移时枚举 $u$ 的下一个点。 当 $u=v$ 时，则可以贡献到 $dp[S]$。对于 $dp[S]$ ，任选两个点 $u,v\in S$ 作为路径端点，转移到 $f[S][u][v]$。 时间复杂度 $O(n^32^n)$。 $f$ 数组所需的空间过大，按 $s$ 中 $1$ 的个数滚动数组，可以将空间复杂度优化至 $O\big(\binom{n}{n/2}n^2\big)$ ```cpp ``` ## [DS] E Chemistry **题意** : 给出一张 $n$ 个点 $m$ 条边的无向图。 求有多少个区间点集 $[l,r]$ 的导出子图为一条链（不一定要以标号为序）。 $n,m\leq 2.\times 10^5$ ，时限$\texttt{5s}$。 ------------ 某个点集的导出子图是一条链的充要条件 ： - 没有环 - 边数等于点数减一（达到上界） - 没有三度点 从左到右枚举右端点，考虑每个左端点对应的区间是否合法。 无环 ：用 LCT + 双指针维护。这会去掉一个前缀。 无三度点 ：维护每个点的度数，双指针。这也会去掉一个前缀。 边数等于点数减一 ： 对于位置 $l$ ，记 $c_l$ 表示点集 $[l,r]$ 的导出子图的边数。 若新加一条边 $(r,u)$ ，则将 $c_{1\sim u}$ 加一。 最终我们要询问有多少 $c_{l}=r-l$ 的位置，只需用线段树维护 $c_l-l$ ，然后区间查询最大值与最大值个数即可。 复杂度 $O(n\log n)$。 ```cpp #include<algorithm> #include<cstdio> #include<vector> #define pb push_back #define MaxN 250500 using namespace std; struct LCT{ struct Node{ int l,r,f;bool fl; inline void rev() {swap(l,r);fl^=1;} }a[MaxN]; inline bool nrt(int u) {return a[a[u].f].l==u||a[a[u].f].r==u;} inline void ladd(int u){ if (a[u].fl){ a[a[u].l].rev(); a[a[u].r].rev(); a[u].fl=0; } } void rot(int u) { int fa=a[u].f,gf=a[fa].f; ladd(fa);ladd(u); if (a[gf].l==fa)a[gf].l=u; if (a[gf].r==fa)a[gf].r=u; a[a[fa].f=u].f=gf; if (a[fa].l==u){ a[a[fa].l=a[u].r].f=fa; a[u].r=fa; }else { a[a[fa].r=a[u].l].f=fa; a[u].l=fa; } } void splay(int u){ ladd(u); while(nrt(u)){ int fa=a[u].f,gf=a[fa].f; if (nrt(fa)&&(a[fa].l==u)==(a[gf].l==fa)) rot(fa); rot(u); } } void access(int u){ int sav=u; for (int v=0;u;v=u,u=a[u].f) {splay(u);a[u].r=v;} splay(sav); } void makrt(int u){access(u);a[u].rev();} int findrt(int u){ access(u); while(a[u].l){ladd(u);u=a[u].l;} splay(u);return u; } void spilt(int u,int v){makrt(u);access(v);} void link(int u,int v){makrt(u);a[u].f=v;} void cut(int x,int y){spilt(x,y);a[x].f=a[y].l=0;} bool chk(int u,int v){return findrt(u)==findrt(v);} }T; struct Node{ int x,c,tg; inline void ladd(int t){tg+=t;x+=t;} }a[MaxN<<2]; inline void up(int u){ int l=u<<1,r=u<<1|1; a[u].x=max(a[l].x,a[r].x); a[u].c=((a[l].x==a[u].x) ? a[l].c : 0) +((a[r].x==a[u].x) ? a[r].c : 0); } int n; void build(int l=1,int r=n,int u=1) { if (l==r){a[u].x=l;a[u].c=1;return ;} int mid=(l+r)>>1; build(l,mid,u<<1); build(mid+1,r,u<<1|1); up(u); } inline void ladd(int u){ if (a[u].tg){ a[u<<1].ladd(a[u].tg); a[u<<1|1].ladd(a[u].tg); a[u].tg=0; } } int wfl,wfr,wfc; void add(int l=1,int r=n,int u=1) { if (wfl<=l&&r<=wfr) {a[u].ladd(wfc);return ;} int mid=(l+r)>>1;ladd(u); if (wfl<=mid)add(l,mid,u<<1); if (mid<wfr)add(mid+1,r,u<<1|1); up(u); } int qry(int l=1,int r=n,int u=1) { if (wfl<=l&&r<=wfr) return a[u].x==wfc ? a[u].c : 0; int mid=(l+r)>>1,ret=0;ladd(u); if (wfl<=mid)ret=qry(l,mid,u<<1); if (mid<wfr)ret+=qry(mid+1,r,u<<1|1); return ret; } vector<int> g[MaxN]; void cut(int u,int r){ for (int i=0;i<g[u].size();i++) if (u<g[u][i]&&g[u][i]<=r)T.cut(u,g[u][i]); } int m,d[MaxN]; void cut2(int u,int r){ for (int i=0;i<g[u].size();i++) if (u<g[u][i]&&g[u][i]<=r)d[g[u][i]]--; } int main() { scanf("%d%d",&n,&m); for (int i=1,u,v;i<=m;i++){ scanf("%d%d",&u,&v); g[u].pb(v);g[v].pb(u); }for (int i=1;i<=n;i++)sort(g[i].begin(),g[i].end()); build(); long long ans=0; for (int r=1,tl=1,tl2=1;r<=n;r++){ for (int i=0;i<g[r].size();i++){ int v=g[r][i];if (v>r)continue; while(T.chk(r,v))cut(tl++,r-1); if (tl<=v)T.link(r,v); while(tl2<=v&&(d[v]==2||d[r]==2))cut2(tl2++,r); if (tl2<=v){d[v]++;d[r]++;} wfl=1;wfr=g[r][i];wfc=1;add(); }wfl=max(tl,tl2);wfr=wfc=r;if (wfl<=wfr)ans+=qry(); }printf("%lld\n",ans); return 0; } ``` ## [??] F Interval Graph **题意** 给出 $n$ 个区间，第 $i$ 个区间为 $[l_i,r_i]$ ，且权值为 $w_i$。 构造一张 $n$ 个顶点的无向图，其中顶点 $u$ 对应区间 $u$。 当且仅当对应的区间对具有非空交集时，两个顶点之间存在一条边。 要删除一些点，使得该图无环。求需要删除的最小点权和。 $n\leq 2.5\times 10^5$ ，时限$\texttt{3s}$。 ------------ 观察发现，图无环等价于每个点至多被区间覆盖两次。 这是经典的费用流问题，可见 [P3358 最长k可重区间集问题](https://www.luogu.com.cn/problem/P3358) - 对于区间 $[l_i,r_i]$ 从 $l_i$ 向 $r_i+1$ 连边，容量为 $1$ ，权值为 $w_i$。 - 对于每个位置 $\overline{x}$ ，从 $\overline{x}$ 向 $\overline{x+1}$ 连边，容量为 $+\infty$ - 且连边 $S\rightarrow \overline{-\infty},\overline{+\infty}\rightarrow T$ ，容量均为 $+\infty$ 这样，一条容量为 $1$ 的流就代表选出一组不交的区间集合。 求容量为 $2$ 的最大费用流即可得到“可以保留的最大点权和”。于是需要求两次最长路。 注意到该图是个 $\rm DAG$ ，利用原式对偶算法，为点 $\overline{u}$ 加势能 $-10^{12}*u$ ，则所有的边就都是负的了，可以使用 $\rm Dijkstra$。 复杂度 $O(n\log n)$。 ```cpp ``` ## [DS] I Query On A Tree 17 $\blacktriangle$ **题意** ：给出一棵 $n$ 个点的有根树，初始时每个点的点权为 $0$。 执行 $q$ 次操作，每次操作为下列两种之一 ： - 将 $u$ 子树内的点权 $+1$ - 将 $u$ 到 $v$ 的简单路径上的点权 $+1$ 。 记 $u$ 的点权为 $A_u$ ，每次操作后，找出一个顶点 $t$ 使得 $\sum\limits_{u=1}^nA_u\times dis(u,t)$ 最小。 若有多个满足条件的点，输出深度最小的，可以证明这样的点是唯一的。 $n,q\leq 10^5$ ，时限$\texttt{2s}$。 ------------ 显然， $t$ 是树的带权重心。 记所有点的点权和为 $S$ ，则最浅带权重心的子树点权和一定严格大于 $S/2$。 将所有顶点按照 $\rm dfs$ 序写出，点 $u$ 重复 $A_u$ 次。 重心的子树是该序列上的一个区间，且长度大于序列长度的一半，。 于是，这个区间一定包含序列最中间的元素（若区间长度为偶数，则可以任取一个） 用重链剖分加线段树维护点权。每次用线段树上二分找到序列最中间的元素，并从该顶点出发向上倍增，找到第一个子树点权和 $>S/2$ 的数即可。 复杂度 $O(n+q\log^2 n)$。 ```cpp #include<algorithm> #include<cstdio> #include<vector> #define pb push_back #define ll long long #define MaxN 100500 using namespace std; vector<int> g[MaxN]; struct TNode{int f,tf,p;}b[MaxN]; int siz[MaxN],dep[MaxN],f[20][MaxN]; void pfs1(int u) { siz[u]=1; for (int i=0,v;i<g[u].size();i++) if (!siz[v=g[u][i]]){ dep[v]=dep[f[0][v]=b[v].f=u]+1; pfs1(v); siz[u]+=siz[v]; if (siz[v]>siz[b[u].p]) b[u].p=v; } } int dfn[MaxN],out[MaxN],tim,tp[MaxN]; void pfs2(int u,int tf) { b[u].tf=tf;dfn[u]=++tim; if (b[u].p)pfs2(b[u].p,tf); for (int i=0;i<g[u].size();i++) if (!b[g[u][i]].tf) pfs2(g[u][i],g[u][i]); out[u]=tim; } struct Node{ int len,tg;ll x; inline void ladd(int c) {tg+=c;x+=1ll*len*c;} }a[MaxN<<2]; inline void up(int u) {a[u].x=a[u<<1].x+a[u<<1|1].x;} int n,wfl,wfr;ll ret,tot,wfk; void build(int l=1,int r=n,int u=1) { a[u].len=r-l+1; if (l==r)return ; int mid=(l+r)>>1; build(l,mid,u<<1); build(mid+1,r,u<<1|1); } inline void ladd(int u){ if (a[u].tg){ a[u<<1].ladd(a[u].tg); a[u<<1|1].ladd(a[u].tg); a[u].tg=0; } } void add(int l=1,int r=n,int u=1) { if (wfl<=l&&r<=wfr) {a[u].ladd(1);tot+=a[u].len;return ;} int mid=(l+r)>>1;ladd(u); if (wfl<=mid)add(l,mid,u<<1); if (mid<wfr)add(mid+1,r,u<<1|1); up(u); } void qry(int l=1,int r=n,int u=1) { if (wfl<=l&&r<=wfr){ret+=a[u].x;return ;} int mid=(l+r)>>1;ladd(u); if (wfl<=mid)qry(l,mid,u<<1); if (mid<wfr)qry(mid+1,r,u<<1|1); } int kth(int l=1,int r=n,int u=1) { if (l==r)return l; int mid=(l+r)>>1;ladd(u); ll ls=a[u<<1].x; if (wfk>ls){wfk-=ls;return kth(mid+1,r,u<<1|1);} return kth(l,mid,u<<1); } void padd(int u,int v) { while(b[u].tf!=b[v].tf){ if (dep[b[u].tf]<dep[b[v].tf])swap(u,v); wfl=dfn[b[u].tf];wfr=dfn[u];add(); u=b[b[u].tf].f; }wfl=dfn[u];wfr=dfn[v]; if (wfl>wfr)swap(wfl,wfr);add(); } void subadd(int u) {wfl=dfn[u];wfr=out[u];add();} ll subqry(int u) {ret=0;wfl=dfn[u];wfr=out[u];qry();return ret;} int calc(int u) { for (int k=16;k>=0;k--){ int v=f[k][u]; if (!v)continue; if (subqry(v)*2<=tot)u=v; }return (subqry(u)*2<=tot) ? f[0][u] : u; } int q; int main() { scanf("%d",&n); for (int i=1,u,v;i<n;i++){ scanf("%d%d",&u,&v); g[u].pb(v);g[v].pb(u); }dep[1]=1;pfs1(1);pfs2(1,1); for (int j=1;j<=16;j++) for (int i=1;i<=n;i++) f[j][i]=f[j-1][f[j-1][i]]; for (int i=1;i<=n;i++)tp[dfn[i]]=i; build(); scanf("%d",&q); for (int i=1,op,u,v;i<=q;i++){ scanf("%d%d",&op,&u); if (op==1)subadd(u); else {scanf("%d",&v);padd(u,v);} wfk=(tot+1)/2; printf("%d\n",calc(tp[kth()])); }return 0; } ``` ## [DS] L Steel Slicing 2 $\blacktriangle$ **题意** ： 给出一张纸片，宽为 $n$。其中第 $i$ 单位宽度向上延伸 $l_i$ ，向下延伸 $r_i$。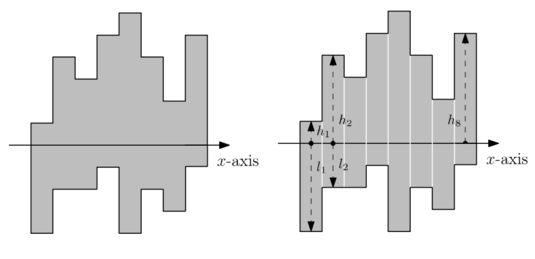  要求对该纸片切若干刀，每一刀都恰好将每一个纸片切成两份，要求切完后所有纸片都是矩形，求最小的刀数。 $n\leq 2.5\times 10^5$ ，时限$\texttt{1s}$。 ------------ 显然，所有刀一定水平切或者竖直切。 又能发现，当图中不存在凹顶点时，则代表所有纸片都是凸多边形。又因为刀法是水平的，所以就都是矩形。 进一步观察，若还有凹顶点，则必定存在一刀减少一个凹顶点的方案。此外，一刀至多减少两个凹顶点。  于是，我们只需最大化切掉两个凹顶点的刀数（称这样的刀是好的）。若总凹顶点个数为 $c$ ，切掉两个凹顶点的刀数为 $d$ ，则总刀数为 $c-d$。 将所有能好的刀痕都画出来，如图所示。  其中，第 $i$ 列与第 $i+1$ 列之间的（竖着的）刀痕是好的，当且仅当 $l_i\neq l_{i+1},r_i\neq r_{i+1}$。 此外，若 $j-i>1,\ l_i=l_j$ 且 $\min_{k=i+1}^{j-1}l_k>l_i$ ，则存在一刀从 $l_i$ 切到 $l_j$ 是好的。 $r$ 的一侧类似。可以利用笛卡尔树求出所有横着的好刀痕，共 $O(n)$ 条。 接下来，我们要选取若干刀痕实际切下。不难发现，一个刀痕集合合法，当且仅当没有两个刀痕在非端点处相交。 刀痕的相交关系可以被描述为二分图，接下来就是要求该二分图的最大独立集大小。可以转化为求最大匹配。 不难发现，每条横刀能匹配的竖刀是一个区间。且这些区间不会部分相交，只会包含或相离。 于是，有简单的贪心策略 ： 从左往右考虑每条竖刀，选择一条右端点尽量靠左的横刀来匹配。 ```cpp ```