fhq treap
JK_LOVER
·
·
个人记录
今天我为大家介绍一下fhq treap
### 1. 前置技能
#### 二叉查找树
二叉查找树满足:
- 二叉树的性质。
- 左儿子的权重小于根。
- 右儿子的权重大于根。
#### 笛卡尔树
- 按第一关键字是一颗二叉查找树。
- 按第二关键字是满足大根堆(小根堆)的性质。
### 2. 操作函数
操作函数中较难理解的也是最重要的两个函数 $\text{split}$(分裂) 和 $\text{merge}$(合并)
#### 1. split(分裂)
$\text{split}$ 函数的作用是将一颗 $\text{fhq treap}$ 按一定关键字分裂成两颗树,以下是一种比较常见的写法。
```cpp
void split(int now,int k,int &x,int &y)
{
if(now == 0) return x = y = 0;
else
{
if(val[now] <= k)
{
x = now;
split(ch[now][1],k,ch[now][1],y);
}
else
{
y = now;
split(ch[now][0],k,x,ch[now][0]);
}
update(now);
}
}
```
##### 进行分析
- 我们可以看出split函数的复杂度是由树高决定的,所以split函数是一个 $O(\log{n})$ 的函数。
- 如果关键字小于(我这里是小于等于)key值,就分在x中,否则分在y中,因为需要修改x,y的大小,这里采用引用达到修改的目的。
- 在分裂树之后树的形态是有所变化的,所以为了保证数据的真确,在函数末要更新当前节点。
再来看看图例:
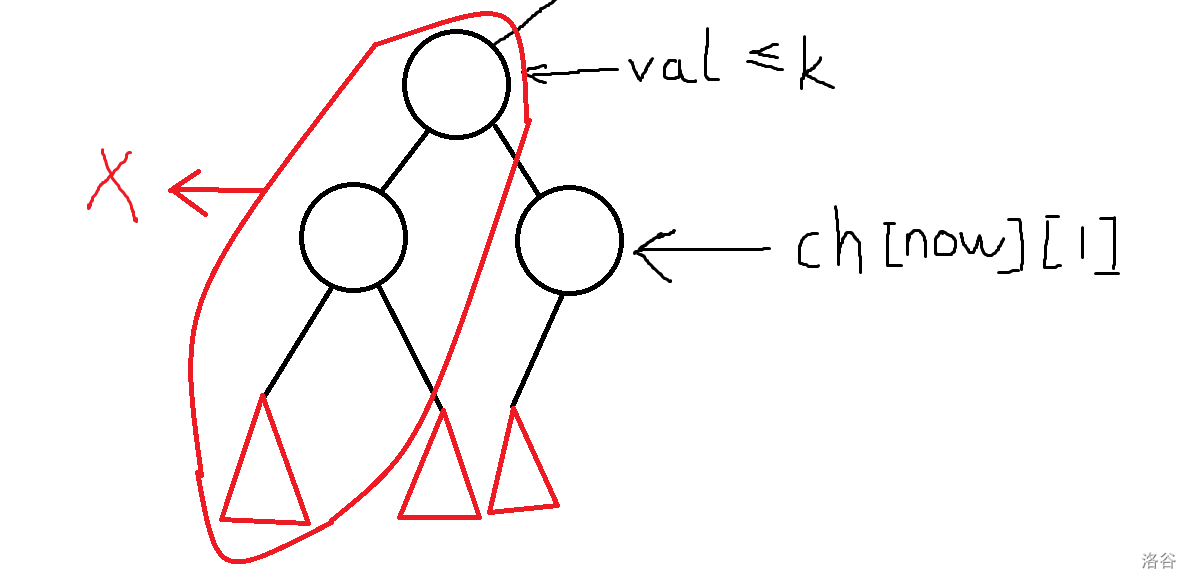
下一步:
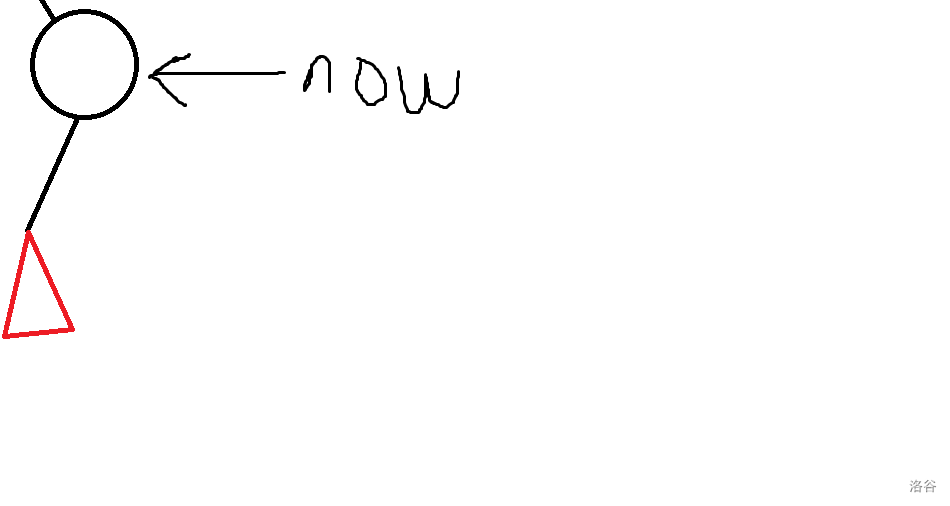
#### 2. merge(合并)
$\text{merge}$ 函数的作用是将两颗树合并的函数,以下是一种常见的写法(这里保证 x 的权值小于 y 的权值)。
```cpp
int merge(int x,int y)
{
if(!x || !y) return x|y;
if(w[x] < w[y])
{
ch[x][1] = merge(ch[x][1],y);
update(x);
return x;
}
else
{
ch[y][0] = merge(x,ch[y][0]);
update(y);
return y;
}
}
```
##### 进行分析
- 我们可以看出merge函数的复杂度是由树高决定的,所以merge函数是一个 $O(\log{n})$ 的函数。
- 如果 x 的第二关键字小于 y 的第二关键字,为了保证笛卡尔树的性质(这里是小根堆),我们就必修把 y 放在 x 的右儿子上,否则就把 x 放在 y 的左子树上。
- 在分裂树之后树的形态是有所变化的,所以为了保证数据的真,在函数末要更新当前节点。
再来看看图例:
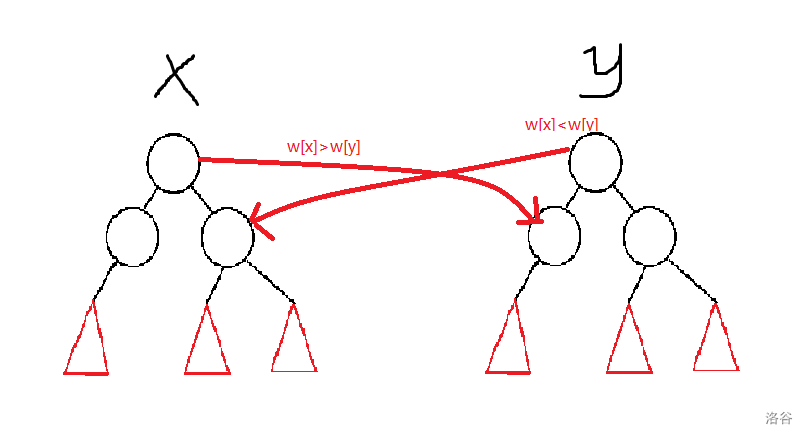
#### 其他函数
- 删除一个点 : 将左右儿子merge。
- 插入一个点 : 将这个点为key值分裂再将三部分merge。
- 求排名: 将这个点为key值分裂再输出树的大小。
- 反转区间: 将区间分裂出来,打上标记放回去。
- 支持正常的平衡树操作。
### 3.建树
#### 第一种 (O(nlogn))
按照 merge 函数可直接建树。
#### 第二种 (O(n))
按照 $\text{笛卡尔树}$ 的性质用栈辅助建树。方式可见洛谷模板
[笛卡尔树](https://www.luogu.com.cn/problem/P5854)
,这里我还是贴一下模板
```cpp
int build(int a[], int k)
{
int root = 0;
for (int i = 1, x, y; i <= k; ++i) {
x = build_point(a[i]), y = 0;
while (top && val[x] < val[s[top]]) { y = s[top--]; push_up(y); }
s[++top] = x;
ch[x][0] = y;
if (top) ch[s[top - 1]][1] = x;
if (top == 1) root = x;
}
while (top) push_up(s[top--]);
return root;
}
```
### 4.可持久化
持久化可以解决各个历史版本的问题或者一些可加减的问题(比较抽象,例如区间第K大之类的)。
我们按照线段树的可持久化来考虑:只有结点个数需要更改时才会复制结点。观测 fhq treap 的构建方式也只有 split 和 merge 需要更改节点信息,所以我们也只需要修改这两函数就行了。
```cpp
int merge(int a,int b)
{
if(!a||!b)return a+b;
if(t[a].rnd>t[b].rnd)
{
int p=++cnt;t[p]=t[a];
t[p].r=merge(t[p].r,b);
update(p);return p;
}
else
{
int p=++cnt;t[p]=t[b];
t[p].l=merge(a,t[p].l);
update(p);return p;
}
}
void split(int now,int k,int &x,int &y)
{
if(!now)x=y=0;
else
{
if(t[now].v<=k)
{
x=++cnt;t[x]=t[now];
split(t[x].r,k,t[x].r,y);
update(x);
}
else
{
y=++cnt;t[y]=t[now];
split(t[y].l,k,x,t[y].l);
update(y);
}
}
}
```