分块他不香吗??
Future_Zero
·
·
个人记录
P1052 过河
传送门
不是吧不是吧,不会所有人都在路径压缩吧
本蒟蒻不会路径压缩,看到m=100,就想到分块了
首先对于这题的状态转移方程,就确实不用讲了:
------------
但是看到$L\le 1e9$我就知道事情没那么简单,这么大谁顶得住啊
其他神犇晃了一眼就想到路径压缩(~~我也想到了,可惜我不会~~),所以看到$m\le 100$自然而然想到分块? (挠头)
把L分成$sqrt(L)$个块,最多40000个块,但是$m\le 100$,含有石子的块最多也就100个而已,**我们只需要处理有石子的块**,没有石子的块管他干嘛
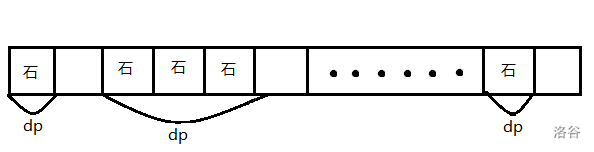
标记有石子的块,在$solve()$中直接$dp$处理,把处理的结果累加起来就是最终结果了,而$f$数组在每个块内都能从零开始,这样空间过了
时间复杂度$O(sqrt(L)*m*t)$也过了
------------
然而你会发现这其中有很多问题:
1.$dp$中我们需要判断某个点是否有石子,但是这里我们无法直接标记,$L$太大了,数组空间会炸,于是想到用$hash$进行判断的(~~用$set$容器也许更方便,但是每次查询时间$log_m$会炸~~)
2.此题起点为0,是真的有点坑,第一个块需要特判
3.相邻的块因为起点终点相接,需要并在一起同时处理
4.关于某个块的起点问题,你不能直接赋$f[0]=0$,毕竟跳出上一个处理过的块后你不一定能刚好跳到现在这一个块的起点,所以我用了一个$last\ end[]$来保存上一个处理的块可能的终点,进而判断现在可能的起点(第一个块需要特判)
------------
u1s1用分块做这道题细节爆炸,~~我调了一晚上~~,考场上还是路径压缩更香(逃)
AC代码(993ms)
望着别人比我短不知道多少的代码跑出30ms的结果我陷入了沉思...
```c
#include<bits/stdc++.h>
using namespace std;
const int M=110,Q=4e4+10,N=4e6+100,INF=0x7f7f7f7f ; //Q=根号L,N=Q*M
int L,s,t,m,pos[M];
bool vis[Q];
/////////////////////////////////////////////////
int q,l[N],r[N];
void pre() //处理分块
{
if(L<=10000) q=1;
else q=sqrt(L);
if(q==1) l[1]=1,r[1]=L;
else for(int i=1;i<=q;++i)
l[i]=(i-1)*q+1,r[i]=i*q;
}
//////////////////////////////////////////////////
int hash[10000]; //反正M=100,多开亿点它不香吗
inline int locate(int x)//找hash下标
{
int tmp=x%837;
while(hash[tmp]&&hash[tmp]!=x) ++tmp;
return tmp;
}
inline int find(int x) //判断是否有x元素
{
if(hash[locate(x)]==x) return 1;
else return 0;
}
/////////////////////////////////////////////////
int f[N],last_end[15],last_cnt;
void init(int start) //赋f的初值
{
memset(f,0x7f,sizeof(f));
if(start==1) for(int i=s;i<=t;++i)//由于起点为0,需要特判
f[i]=find(i);
else for(int i=start;i<=start+t;++i)
for(int j=1;j<=last_cnt;++j)
for(int k=s;k<=t;++k)
if(!((i-last_end[j])%k)) f[i-start+1]=0;
}
int solve(int start,int end)
{
init(start);//初始化
int len=end-start+1;
for(int j=0;j<=len;++j)
{
for(register int k=s;k<=t;++k)
{
int pos=start+j-1+k,to=j+k; //pos是跳至实际位置,j是现在块中的位置,to是跳至块中的位置
int num=f[j]+find(pos);//若pos有石子则+1,否则+0
f[to]=min(f[to],num);
}
}
int ans=INF;
for(int i=len-t;i<=len;++i) //记下所有可满足最小ans的可能终点
if(f[i]<ans) ans=f[i],last_cnt=1,last_end[1]=start+i-1;
else if(f[i]==ans) last_end[++last_cnt]=start+i-1;
return ans;
}
//////////////////////////////////////////////////
int main()
{
scanf("%d%d%d%d",&L,&s,&t,&m);
pre();//分块的处理
for(int i=1;i<=m;++i)
{
int x;
scanf("%d",&x);
hash[locate(x)]=x; //输入石子位置加入mp
int INK=lower_bound(r+1,r+1+q,x)-r;//找x所在区块
vis[INK]=true; //标记x所在区块有石子
}
int ans=0;
for(int i=s;i<=t;++i)
last_end[++last_cnt]=i;
for(int i=1;i<=q;++i)
{
if(!vis[i]) continue;
int start=i,end=i; //相邻的块因为起点终点相接,需要并在一起同时处理
while(vis[i+1]) ++i,++end; //找到此次处理的区块区间[start,end]
ans+=solve(l[start],min(L,r[i]));
}
printf("%d\n",ans);
}
```
于是题解满了就很淦