惯性力
_sys
·
·
个人记录
so freaking hard.
极坐标系分解
对一点 P(r, \theta),朝 \textbf r 延长方向设置径向方向矢量 \textbf e_r,朝逆时针方向设置与 \textbf e_r 垂直的横向方向矢量 \textbf e_\theta,\textbf e_r, \textbf e_\theta 便构成一组活动正交基矢,方向会随着 \theta 改变。在该平面上矢量 A 可分解成 A_r \textbf e_r+A_\theta \textbf e_\theta。则有:
\textbf r=r\textbf e_r
\mathrm d\textbf e_r=\mathrm d\theta \textbf e_\theta, \mathrm d\textbf e_\theta=- d \theta \textbf e_r
\textbf v=\frac{\mathrm d\textbf r}{\mathrm dt}= \frac{\mathrm d(r \textbf e_r)}{\mathrm dt}=\frac{\mathrm dr}{\mathrm dt} \textbf e_r+r \frac{\mathrm d \textbf e_r}{\mathrm dt}=\frac{\mathrm dr}{\mathrm dt} \textbf e_r+r\frac{\mathrm d \theta}{\mathrm dt} \textbf e_\theta
其中
\textbf v_r=\frac{\mathrm dr}{\mathrm dt}\textbf e_r, \textbf v_\theta=r\frac{\mathrm d \theta}{\mathrm dt}\textbf e_\theta
被称为径向速度和横向速度。
接下来考虑加速度。
\begin{aligned}\textbf a=&\frac{\mathrm d \textbf v}{\mathrm dt} =\frac{\mathrm d}{\mathrm dt}\left(\frac{\mathrm dr}{\mathrm dt} \textbf e_r\right)+\frac{\mathrm d}{\mathrm dt}\left(r\frac{\mathrm d \theta}{\mathrm dt}\textbf e_\theta\right) \\ =&\left(\frac{\mathrm d^2r}{\mathrm dt^2} \textbf e_r+\frac{\mathrm dr}{\mathrm dt} \frac{\mathrm d\textbf e_r}{\mathrm dt}\right)+\left(\frac{\mathrm d r}{\mathrm dt} \frac{\mathrm d \theta}{\mathrm dt} \textbf e_\theta+r \frac{\mathrm d^2 \theta}{\mathrm dt^2} \textbf e_\theta+ r \frac{\mathrm d \theta}{\mathrm dt} \frac{\mathrm d \textbf e_\theta}{ \mathrm dt}\right) \\ =&\left(\frac{\mathrm d^2r}{\mathrm dt^2}-r \left(\frac{\mathrm d\theta}{\mathrm dt}\right)^2\right)\textbf e_r+\left(2 \frac{\mathrm dr}{\mathrm dt}\frac{\mathrm d \theta}{\mathrm dt}+r\frac{\mathrm d^2 \theta}{\mathrm dt^2}\right)\textbf e_\theta \\ =&\textbf a_r+\textbf a_\theta\end{aligned}
两者分别称作径向加速度和横向加速度。
将 r=r(t), \theta=\theta(t) 中的 t 消去,可得极坐标系中的质点运动轨道方程 r=r(\theta)。
为便于描述极坐标系的旋转,将角位移、角速度、角加速度矢量化为 \bm \theta, \bm \omega, \bm \beta。
定义方向矢量 \bm k, 则定义 \bm \theta= \theta \bm k,\omega=\frac{\mathrm d \bm \theta}{ \mathrm dt}= \frac{\mathrm d \theta}{\mathrm dt} \bm k = \omega \bm k,\bm \beta = \beta\bm k。注意他们的单位不同,但都表示在同一条线上。
根据右手定则定义叉积 \times。则有
\mathrm d \bm R = \mathrm d \bm \theta \times \bm R
\bm v = \bm \omega \times \bm R
\bm a = \bm \beta \times \bm R + \bm \omega \times \bm v
根据方向可知,其中第一项为 \bm a_{\text{切}},第二项为 \bm a_{\text{心}}。
惯性系
按照牛顿主义的观点,遵循牛顿三定律的参考系为惯性系,否则为非惯性系。可知相对惯性系做匀速直线运动的为惯性系,做加速运动的为非惯性系。存在除去所有物质的绝对空间-其为第一个惯性系,确立了其他所有惯性系。
运动是相对的,参考系之间的运动也是相对的。惯性系之间的关系是平等的,不存在绝对静止与匀速运动的二元性。但是惯性系与非惯性系之间的关系不是对称的。
在非惯性系中,第二定律不成立。因为在牛顿力学理论看来,力与质量是真实的,不随参考系改变。故需要引入假象的力 F_{\text{虚}},使得 F'=F+F_{\text{虚}} 能够满足 F'=ma',则可以将其视作惯性系处理。
***
我们将非惯性系相对于惯性系做的加速运动分解为平动和转动。惯性力类别分别对应平移惯性力;惯性离心力、科里奥利力与切向惯性力。
## 平移惯性力
设非惯性系 $S'$ 相对于惯性系 $S$ 作变速平动,加速度为 $a_0$,质点 $m$ 相对于 $S$ 的加速度为 $a$,则
$$F=ma$$
质点 $m$ 相对 $S'$ 系的加速度为
$$a'=a+(-a_0)$$
故引入平移惯性力 $F_i=m(-a_0)$,使得
$$F'=F+F_i, F'=ma'$$
## 惯性离心力、科里奥利力与切向惯性力
非惯性系 $S'$ 以角速度 $\bm \omega$,角加速度 $\bm \beta$ 绕惯性系 $S$ 的 $z$ 轴匀速旋转,两系坐标原点 $O$ 重合。$z$ 轴重合。时间 $t$ 重合。
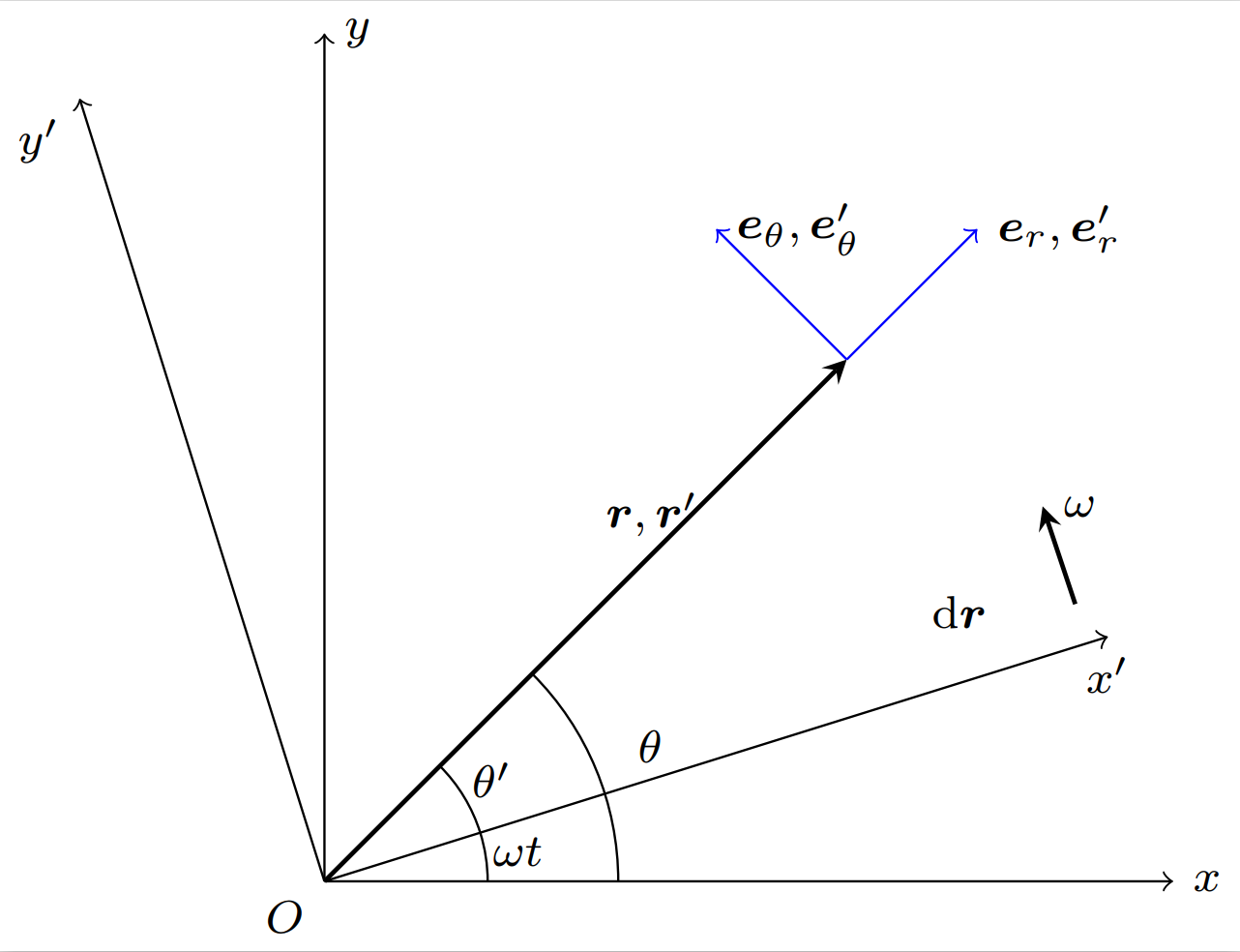
任一质点在极坐标系的量及其对时间的微分关系为
$$r=r', \theta = \theta' + \omega t$$
$$\frac{\mathrm dr}{\mathrm dt}=\frac{\mathrm dr'}{\mathrm dt}, \frac{\mathrm d^2r}{\mathrm dt^2}=\frac{\mathrm d^2r'}{\mathrm dt^2}$$
$$\frac{\mathrm d \theta}{\mathrm dt} =\frac{\mathrm d \theta'}{\mathrm dt} + \omega, \frac{\mathrm d^2 \theta}{\mathrm dt^2} =\frac{\mathrm d^2 \theta'}{\mathrm dt^2}+\beta$$
由于我们在描述同一个质点,故 $\bm e_r=\bm e_r', \bm e_\theta = \bm e_\theta'$。
质点在 $S'$ 中的速度、加速度为
$$v_r'=\frac{\mathrm dr'}{\mathrm dt}, v_\theta'=r'\frac{\mathrm d \theta'}{\mathrm dt}$$
$$a_r'=\left(\frac{\mathrm d^2r'}{\mathrm dt^2}-r' \left(\frac{\mathrm d\theta'}{\mathrm dt}\right)^2\right), a_\theta'=\left(2 \frac{\mathrm dr'}{\mathrm dt}\frac{\mathrm d \theta'}{\mathrm dt}+r\frac{\mathrm d^2 \theta'}{\mathrm dt^2}\right)$$
我们将其代入 $a_r, a_\theta$ 得
$$\bm a_r=\left(\frac{\mathrm d^2r}{\mathrm dt^2}-r\left(\frac{\mathrm d \theta}{\mathrm dt}\right)^2\right)\bm e_r=\left(\frac{\mathrm d^2r'}{\mathrm dt^2}-r\left(\frac{\mathrm d \theta'}{\mathrm dt}+\omega\right)^2\right)\bm e_r'=\bm a_r'-2 \bm v_\theta' \times \bm \omega-\omega^2 \bm r'$$
$$\bm a_\theta= \left(2 \frac{\mathrm dr}{\mathrm dt}\frac{\mathrm d \theta}{\mathrm dt}+r\frac{\mathrm d^2 \theta}{\mathrm dt^2}\right)\bm e_\theta=\left(2 \frac{\mathrm dr'}{\mathrm dt}\left(\frac{\mathrm d \theta'}{\mathrm dt} + \omega\right)+r\left(\frac{\mathrm d^2 \theta'}{\mathrm dt^2}+\beta\right)\right)\bm e_\theta'=\bm a_\theta'-2 \bm v_r'\times \bm \omega-\bm r' \times \bm \beta$$
那么
$$m(\bm a_r'+\bm a_\theta')=m(\bm a_r+\bm a_\theta)+m \omega^2 \bm r'+2m \bm v' \times \bm\omega+ m \bm r' \times \bm \beta$$
$$\bm F=m(\bm a_r+\bm a_\theta)$$
为满足 $\bm F'=m(\bm a'_r+\bm a'_\theta)$,引入与位置有关的惯性离心力、与速度有关的科里奥利力和与和角加速度有关的切向惯性力。
$$\bm F_c=m \omega^2 \bm r'$$
$$\bm F_{\textrm{Cor}}=2m\bm v' \times \bm \omega$$
$$\bm F_t=m \bm r' \times \bm\beta$$